PhysProf - Zerstreuungslinsen - Bild - Simulation - Brennpunkt
Fachthemen: Zerstreuungslinse - Brennweitenbestimmung - Konkave Linsen - Reelle Bilder - Virtuelle Bilder
PhysProf - Geometrische Optik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.
Online-Hilfe für das Modul
zur Darstellung des Strahlenverlaufs der bei Lichtbrechungen an Zerstreuungslinsen entsteht.
Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden physikalischen Sachverhalte und eignet sich zudem als Begleitung zu Versuchen im Physikunterricht.
Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.
Weitere relevante Seiten zu diesem Programm
Themen und Stichworte zu diesem Modul:Linse - Zerstreuungslinse - Streulinse - Optische Linsen - Strahlen - Geometrische Optik - Berechnen - Konkave Linse - Konkavlinse - Bikonkave Linse - Zerstreuungslinsen - Streulinsen - Optische Linse - Dünne Linsen - Dünne Linse - Dicke Linse - Dicke Linsen - Gegenstandsweite - Bildweite - Reelles Bild - Virtuelles Bild - Parallelstrahl - Parallelstrahlen - Brennpunktstrahl - Bestimmung - Bestimmen - Reelle Abbildung - Reelle Bilder - Virtuelle Bilder - Linsenabbildung - Abbildung - Bildgröße - Gegenstandsgröße - Brechwert - Brechkraft - Brennweite - Brennpunkt - Abbildungsmaßstab - Zeichnen - Fokus - Focal length - Bildpunkt - Brennebene - Licht - Einheit - Was - Wie - Weshalb - Was ist - Warum - Erklärung - Einfach erklärt - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Aufgaben - Lösungen - Optische Achse - Eigenschaften - Linsengleichung - Abbildungsgesetz - Abbildungsgleichung - Gleichung - Konkav - Bildentstehung - Linsen - Arten - Linsenarten - Linsenformen - Plankonkav - Plankonkave Linse - Konkave Linsen - Strahlenverlauf - Strahlengang - Strahlenoptik - Aufbau - Abbilden - Optik - Grundlagen - Grundlegendes - Animation - Physik - Unterricht - Versuch - Physikalisch - Rechner - Beispiele - Zeichnen - Physikalische Formel - Formel - Formelzeichen - Bild - Grafik - Berechnung - Darstellen - Grafische Darstellung - Hauptebene - Hauptebenen |
 |  |
Zerstreuungslinse
Modul Zerstreuungslinse
Mit Hilfe des Unterprogramms [Optik] - [Zerstreuungslinse] kann die Entstehung eines Bildes an konkaven dünnen Linsen dargestellt, sowie der hierbei entstehende Strahlenverlauf grafisch analysiert werden.
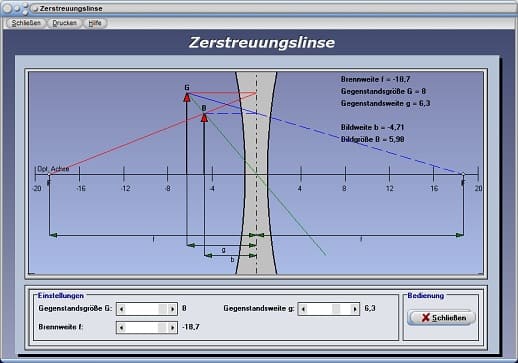
Zerstreuungslinse - Abbildung 1
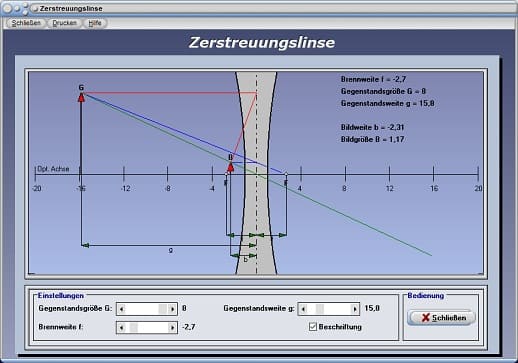
Zerstreuungslinse - Abbildung 2
Die geometrische Optik beschreibt optische Erscheinungen (Vorgänge) mit Hilfe von Lichtstrahlen unter Verwendung der Geometrie und behandelt den Weg des Lichts sowie dessen Ausbreitungsrichtung auf Linien. Die Strahlenoptik benutzt geometrische Konstruktionen zur Beschreibung des Strahlengangs von Lichtstrahlen auf Linien. Sie bedient sich des Strahlenmodells des Lichts.
Als Linse wird ein optisch wirksames Bauelement mit zwei lichtbrechenden Flächen, von welchen mindestens eine dieser konvex oder konkav gewölbt ist, bezeichnet. Eine gedachte Linie, auf welcher die Krümmungsmittelpunkte der Linsenflächen liegen, wird optische Achse genannt. Optische Linsen finden bei der Bündelung oder der Streuung von Licht Einsatz. Eine optische Linse dient dazu, Gegenstände optisch zu verkleinern oder zu vergrößern.
Zerstreuungslinsen zeichnen sich dadurch aus, dass sie mittels zweier Kugelflächen derart begrenzt sind, dass sie in der Mitte dünner sind als am Rand. Eine Zerstreuungslinse trägt auch die Bezeichnung Konkavlinse bzw. konkave Linse oder Streulinse. Als konkav wird eine nach innen gewölbte Fläche bezeichnet. Parallel zur optischen Achse durch eine Konkavlinse tretende Strahlen werden so gebrochen als kämen sie von einem vor der Linse liegenden Brennpunkt F.
Dessen Abstand von der Linie ist die Brennweite f. Sie ist stets negativ. Die Brennweite einer Linse hängt vom Linsenmaterial, den Krümmungsradien, den begrenzenden Kugelflächen und dem umgebenden Medium ab. Es gilt:
Die Abbildungsgleichung (Linsengleichung) beschreibt bei einer Linsenabbildung die Beziehung zwischen Bildweite, Gegenstandsweite, Bildgröße und Gegenstandsgröße. Sie wird auch als Abbildungsgesetz bezeichnet und ist wie folgt definiert:
Der Abbildungsmaßstab A beschreibt das Verhältnis von Bildgröße zu Gegenstandsgröße. Für ihn gilt:
A = B/G
Hierbei sind:
A: Abbildungsmaßstab
G: Gegenstandsgröße [m]
B: Bildgröße [m]
g: Gegenstandsweite [m]
b: Bildweite [m]
f: Brennweite [m]
Als Gegenstandsweite ist der Abstand des Gegenstands von der Mitte der Linse definiert. Die Brennweite gibt den Abstand des Brennpunktes von der Linse an. Die Gegenstandsgröße ist die Höhe des Gegenstands. Unter Bildweite versteht sich der Abstand des entstandenen Bildes von der Linsenmitte und die Bildgröße beschreibt die Höhe des Bildes.
Als Brennpunkt (Fokus) wird in der Optik ein Punkt bezeichnet, in welchem eine optische Linse sämtliche parallel verlaufenden Lichtstrahlen sammelt.
Der Parallelstrahl ist eine Hilfe zur Konstruktion des Strahlengangs eines optischen Systems. Parallelstrahlen werden an der Linse gebrochen und verlassen diese in Form von Brennpunktstrahlen. Als Brennpunktstrahl wird ein Lichtstrahl bezeichnet, der durch einen Brennpunkt einer Linse verläuft.
Mit dem Ausdruck Strahlengang (Strahlenverlauf) wird in der Optik der Verlauf von Lichtstrahlen beschrieben, die durch optische Geräte verlaufen.
In diesem Modul kann die Bildentstehung durch Zerstreuungslinsen analysiert werden.
Programmbedienung
Das Programm stellt die maßgeblich wichtigsten Strahlen dar, welche zur Erstellung des Bildes notwendig sind. Dies sind der Brennpunktstrahl (blau), der Mittelpunktstrahl (grün) und der Parallelstrahl (rot).
Mit Hilfe der zur Verfügung stehenden Rollbalken können Sie die Brennweite f, die Gegenstandsweite g, sowie die Gegenstandsgröße G einstellen. Daraufhin wird die Darstellung des Bildes aktualisiert.
Die errechneten Werte für die Bildweite b und Bildgröße B werden ausgegeben. Eine Aktivierung des Kontrollkästchens Beschriftung bewirkt die Beschriftung der Grafik mit den Bezeichnungen für Gegenstandsweite, Bildweite und Brennweite.
Die Brennweite einer Linse hängt von folgenden Faktoren ab:
- Brechzahl des Materials der Linse
- Brechzahl des Materials der Umgebung
- Krümmungsradien der Linsen (Kugelflächen)
Als Brechwert (Brechkraft) wird der Kehrwert der Brennweite bezeichnet.
Nachfolgend wird auf die Bestimmung der Brennweite einer oder mehrerer Linsen eingegangen.
1. Brennweite bestimmen für eine dünne Linse:
Als dünne Linse wird eine Linse bezeichnet, deren Dicke in Relation zu den Radien ihrer brechenden Außenseiten gering ist. Die Brennweite einer dünnen Linse kann wie folgt bestimmt werden:
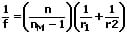
f: Brennweite der Linse
n: Brechzahl des Materials der Linse
nM: Brechzahl des Materials der Umgebung
r1: Krümmungsradius der stärker gekrümmten Linsenseite
r2: Krümmungsradius der weniger stark gekrümmten Linsenseite
2. Brennweite bestimmen für zwei dünne Linsen:
Wenn der Abstand d zweier Linsen gering ist gegenüber den Brennstrahlen f1 und f2, dann wirken derartige Systeme wie eine einzelne Linse. Die (gesamte) Brennweite solcher Systeme kann aus den einzelnen Brennweiten bestimmt werden.
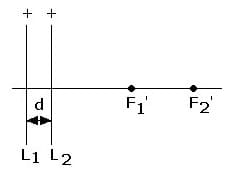
L1,L2: Linse 1, Linse 2
d: Abstand der beiden Linsen L1 und L2
F1,F2: Brennpunkte der beiden Linsen L1 und L2
Abb. 1: System zweier dünner Linsen
Für ein System mit zwei dünnen Linsen gilt für die Brennweite:
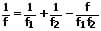
f: Brennweite des Systems zweier Linsen
f1: Brennweite der Linse 1
f2: Brennweite der Linse 2
d: Abstand der beiden Linsen
n: Brechzahl des Materials der Linse
3. Brennweite bestimmen für eine dicke Linse:
Als dicke Linsen werden Linsen bezeichnet, deren Dicke nicht klein genug in Bezug zu ihrer Brennweite ist. Mit dem Begriff Hauptebene wird die Mitte eines Linsensystems bezeichnet. Hauptebenen stehen stets im rechten Winkel zur optischen Achse. Bei dünnen Linsen können die beiden auftretenden Brechungen durch eine Mittelebene ersetzt werden. Bei dicken Linsen hingegen besitzen die Brechungsgesetze lediglich dann Gültigkeit, wenn der Brennpunktstrahl und der Parallelstrahl in unterschiedlichen Hauptebenen gebrochen werden. Die Abstände f, f', g und b beziehen sich in diesem Fall auf die jeweilige Hauptebene.
Abb. 3: Eine Hauptebene (dünne Linse)
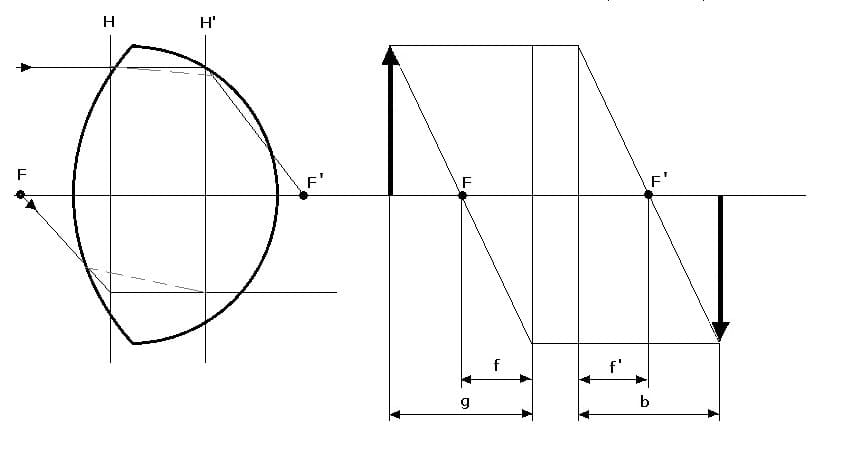
H,H': Hauptebenen
F,F': Brennpunkte der beiden Linsen
f,f',g,b: Brennweiten und Abstände in Bezug zur Hauptebene
Abb. 4: Zwei Hauptebenen (dicke Linse)
Die Brennweite einer dicken Linse lässt sich wie folgt errechnen:
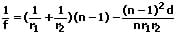
f: Brennweite der dicken Linse
n: Brechzahl des Materials der Linse
r1: Krümmungsradius der stärker gekrümmten Linsenseite
r2: Krümmungsradius der weniger stark gekrümmten Linsenseite
d: Abstand der Scheitel beider Linsen
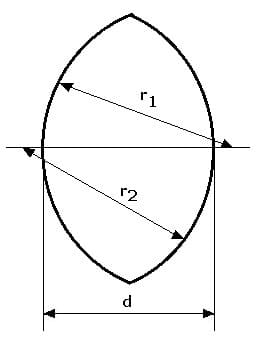
Abb. 5: Krümmungsradien r1 und r2 dicker Linsen
r1: Krümmungsradius der stärker gekrümmten Linsenseite
r2: Krümmungsradius der weniger stark gekrümmten Linsenseite
d: Abstand der Scheitel beider Linsen
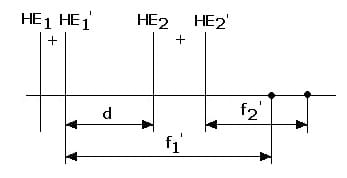
HE1,HE1',HE2,HE2: Hauptebenen
d: Abstand der Scheitel beider Linsen
f,f': Brennweiten in Bezug zur Hauptebene
Abb. 6: Brennweitenbestimmung dicker Linsen
Hinsichtlich ihrer Zuordnung werden konkave Linsen (Zerstreuungslinsen), wie nachfolgend gezeigt, in folgende Arten (Linsenarten bzw. Linsenformen) unterteilt:
- bikonkave Linse
- plankonkave Linse
- konvex konkave Linse
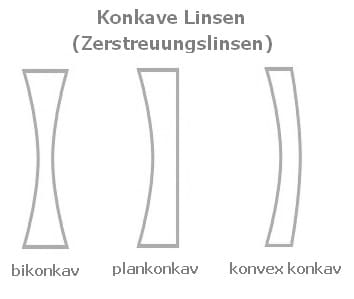
Konkave Linsen sind bezüglich ihrer Kugelflächen in der Mitte dünner als am Rande.
Eine bikonkave Linse besitzt auf beiden ihrer Seiten eine nach innen gewölbte Fläche, divergiert einfallendes Licht und bildet ausschließlich virtuelle Bilder.
Eine plankonkave Linse verfügt auf einer ihrer beiden Seiten über eine nach innen gewölbte Fläche. Ihre zweite Seite ist flach (plan). Sie divergiert parallele eingehende Strahlen und besitzt eine negative Brennweite.
Ist eine Seite einer Linse konvex und die andere Seite konkav gewölbt, so wird von einer konvex-konkaven Linse gesprochen.
Virtuelles Bild:
Bilder, von denen am wahrgenommenen Ort keine Lichstrahlen ausgehen werden als virtuelle Bilder bezeichnet. Sie können an dem Ort an dem sie erscheinen, nicht auf einen Schirm abgebildet werden. Bilder dieser Art ergeben sich in Form von Spiegelbildern oder bei Lupen.
Eigenschaften des virtuellen Bildes:
- Vom wahrgenommenen Ort eines Bildes gehen in Wirklichkeit keine Lichtstrahlen aus
- Ein derartiges Bild kann nicht mithilfe eines Schirms aufgefangen werden
- Es entsteht bei Abbildungen an Zerstreuungslinsen oder an Spiegeln
Relles Bild (reelle Abbildung):
Als reelle Bilder werden Bilder bezeichnet, von welchen reelle Lichtstrahlen ausgehen. Bilder dieser Art entstehen unter anderem bei Abbildungen von Sammellinsen, wenn die Gegenstandsweite größer ist als die Bildweite, bzw. wenn gilt g > f.
Eigenschaften des reellen Bildes:
- Vom Ort des Bildes gehen Lichtstrahlen aus
- Es kann mithilfe eines Schirms aufgefangen und auf diesem abgebildet werden
- Es entsteht bei Abbildungen an Sammellinsen
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Linse sowie unter Wikipedia - Brennweite zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
Reflexion - Lichtbrechung - Sammellinse - Hohlspiegel - Reflexion am Spiegel - Beugung am Spalt - Plancksches Strahlungsgesetz
Unterprogramm Zerstreuungslinse
PhysProf 1.1 - Unterprogramm RLC-Kreis
MathProf 5.0 - Unterprogramm Kurven in Parameterform
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Physik interaktiv
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
Eine Übersicht aller in MathProf 5.0 zur Verfügung stehender Programmteile finden Sie im MathProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
