PhysProf - Widerstandsgesetz - Widerstand - Temperatur

Fachthemen: Widerstand - Temperatur - Joulesches Gesetz

PhysProf - Elektrotechnik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.

Online-Hilfe für das Modul
zur Durchführung einfacher Berechnungen zu Leiterwiderstand und Widerstandsgesetz.

Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.

 

Themen und Stichworte zu diesem Modul: Spezifischer elektrischer Widerstand - Spezifischer elektrischer Leitwert - Elektrischer Widerstand - Leiterwiderstand - Temperaturverhalten - Widerstandsänderung - Elektrischer Leiter - Elektrische Leiter - Leitwert - Leitfähigkeit - Leiter - Durchmesser - Leiterdurchmesser - Leiterquerschnitt - Leitungslänge - Temperatur - Temperaturkoeffizient - Elektrischer Leitwert - Joulesche Wärme - Joulesches Gesetz - Stromwärme - Stromwärmegesetz - Elektrische Leitfähigkeit - Temperaturabhängiger Widerstand - Temperaturabhängkeit - Kennlinie - Kennlinien - UI Kennlinie - IU Kennlinie - Strom-Spannungs-Kennlinie - Strom Spannung Kennlinie - Widerstandskennline - Linearer Widerstand - Nichtlinearer Widerstand - Kurve - Draht - Drähte - Konstantan - Konstantandraht - Kupfer - Aluminium - Silber - Heißleiter - Kaltleiter - Spezifischer Widerstand - Elektrotechnik - E-Technik - Physik - Herleitung - Beweis - Begriff - Begriffe - Einführung - Erklärung - Einfach erklärt - Was - Wie - Weshalb - Was ist - Warum - Bedeutung - Was bedeutet - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Aufgaben - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Spezifischer Leitwert - Widerstand - Kehrwert - Negativer Temperaturkoeffizient - Positiver Temperaturkoeffizient - Leitung - Leitungsquerschnitt - Leiterlänge - Querschnitt - Tabelle - Formel - Formelbuchstabe - Beispiel - Einheit - Rechner - Widerstände - Berechnen

    

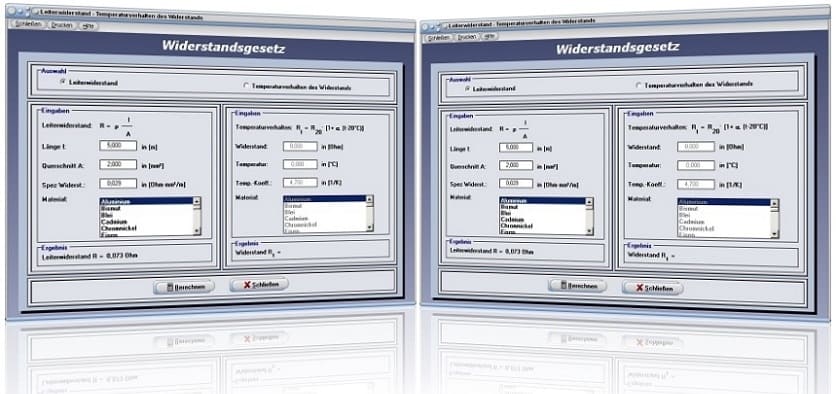
Modul Widerstandsgesetz

---

 
Mit Hilfe des kleinen Unterprogramms [Elektrotechnik] - [Widerstandsgesetz] lassen sich einfache Berechnungen zum Verhalten von Widerständen unter dem Einfluss von Wärme, sowie zum Widerstand von Leitern durchführen.
 

Widerstandsgesetz - Abbildung 1


Widerstandsgesetz - Abbildung 2

Elektrische Leiter: Ein elektrischer Leiter ist ein Medium, welches frei bewegliche Ladungsträger besitzt und diese zum Transport geladener Teilchen verwendet. Als typische elektrische Leiter seien Metalle (z.B. Kupfer, Silber, Platin, Gold) aufgeführt.
 

I - Leiterwiderstand (spezifischer elektrischer Widerstand):

Der spezifische elektrische Widerstand (auch Leiterwiderstand oder spezifischer Widerstand) eines Leiters ist eine temperaturabhängige Materialkonstante. Der elektrische Widerstand eines homogenen Leiters lässt sich aus den Werten des Stoffes errechnen, aus welchem dieser besteht. Er ist temperaturabhängig und wird ermittelt für einen Leiter (Draht), der die Länge 1 m und den Querschnitt 1 mm² bei einer Temperatur von 20° C besitzt. Für ihn gilt:
 

 

Der Kehrwert des spezifischen Widerstands wird als elektrische Leitfähigkeit (auch spezifischer Leitwert oder spezifischer elektrischer Leitwert) bezeichnet. Für ihn gilt:
 

 
Die Leitungslänge (Leiterlänge) l gibt die Länge der berechnenden Leitung an. Der Querschnitt eines Leiters (Leiterquerschnitt oder Leitungsquerschnitt) errechnet sich aus seinem Durchmesser, dem Leiterdurchmesser wie folgt:
 
A = πd²/4


Hierbei sind:

R: Widerstand des Leiters [Ω]

ρ: Spez. elektrischer Widerstand des Materials [ Ωm]

C: Kehrwert des spez. elektrischen Widerstands des Materials [1/[ Ωm]]

l: Länge des Leiters (Leiterlänge, Leitungslänge) [m]

A: Querschnitt des Leiters [m²]
d: Durchmesser des Leiters [m]
 

Der Widerstand eines metallischen Leiters wächst mit zunehmender Temperatur. Bei Halbleitern hingegen sinkt dieser beträchtlich.
 

II - Temperaturverhalten des Widerstands (Widerstandsänderung in Abhängigkeit von der Temperatur):

Da elektrische Widerstände temperaturabhängig sind, ist es notwendig deren Verhalten diesbezüglich zu berechnen. Es gilt:
 

 

Hierbei sind:

R_t: Widerstand des Leiters bei Temperatur t [Ω]

R₂₀: Widerstand des Leiters bei 20°C [Ω]

α: Temperaturkoeffizient des Widerstands für 20°C [1/K]

t: Temperatur [°C]
 

Der Temperaturkoeffizient α des elektrischen Widerstands ist das Verhältnis der relativen Änderung des Widerstands zur Temperaturänderung. Für ihn gilt:



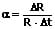
α: Temperaturkoeffizient [1/K]
ΔR: Relative Änderung des Widerstands [Ω]
R: Widerstand [Ω]
Δt: Temperaturänderung [K]
  

Programmbedienung

 
Wählen Sie durch die Aktivierung des entsprechenden Kontrollschalters Leiterwiderstand bzw. Temperaturverhalten des Widerstands, zu welchem Fachthema Sie Werte ermitteln lassen möchten.

Um Berechnungen mit Leiterwiderständen durchführen zu lassen, geben Sie in die dafür vorgesehenen Felder die Werte für die Länge l und den Querschnitt A des Leiters ein. Wird aus der darunter angeordneten Listbox ein Material selektiert, so trägt das Programm den zugehörigen Wert für den spezifischen Widerstand des gewählten Materials in das dafür vorgesehene Eingabefeld ein. Nach einer Bedienung der Schaltfläche Berechnen gibt das Programm das Ergebnis für den Leiterwiderstand R aus.

Sind Berechnungen bzgl. des Temperaturverhaltens eines Widerstands durchzuführen, so geben Sie in die dafür vorgesehenen Felder die Werte für den Widerstand sowie für die vorherherrschende Temparatur ein. Wird aus der darunter angeordneten Listbox ein Material selektiert, so trägt das Programm den zugehörigen Wert für den Temperaturkoeffizienten des gewählten Materials in das dafür vorgesehene Eingabefeld ein. Nach einer Bedienung der Schaltfläche Berechnen wird das Ergebnis für den Wert des Widerstands R_t ausgegeben, den dieser bei der entsprechenden Temperatur besitzt.
 

 
Bei einem Konstantandraht handelt es sich um ein Legierung, die sich aus 54 % Kupfer, 45 % Nickel sowie 1 % Mangan zusammensetzt. Diese Widerstandslegierung wird mit dem Begriff Konstantan bezeichnet und besitzt bis hin zu einer Temperatur von 400° C einen nahezu konstanten spezifischen Widerstand und somit einen innerhalb dieses Bereichs gleichbleibenden elektrischen Widerstand.

Nnachfolgend sind einige wesentliche physikalische Eigenschaften dieser Metalllegierung aufgeführt:
 

Dichte ρ	8,8 g/cm³
Spezifische Wärmekapazität c	0,43 KJ/(kg·K)
Spezifischer elektrischer Widerstand ρ	0,51 Ω⋅mm²/m

 
 

 
Mit Hilfe der Strom-Spannungs-Kennlinie (UI Kennlinie oder Widerstandskennline) eines elektrischen Widerstands (Leiters oder Bauelements) kann der zwischen elektrischem Strom und Spannung bestehende Zusammenhang hinsichtlich dem entsprechenden Bauteil grafisch dargestellt werden. Sie dient unter anderem der Darstellung und Auswertung dessen diesbezüglich vorhandener elektrischer Eigenschaften. Es stellt das Leistungsverhalten eines entsprechenden Bauteils dar. Ein elektrischer Widerstand wird als linearer Widerstand bezeichnet, wenn sich eine daran anliegende Spannung sowie die Stärke des hindurchfließenden elektrischen Stromes zueinander proportional verhalten. Die Strom-Spannungs-Kennlinie bei einem linearen Widerstand stellt eine Gerade dar.


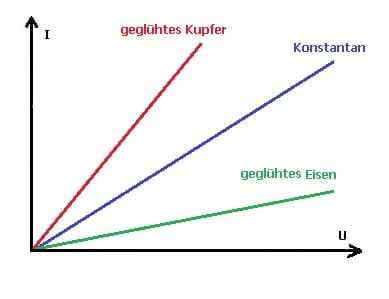
Abb. 1: Strom-Spannungs-Kennline - Ohmsche Widerstände


Temperaturabhängiger Widerstand:

Widerstände sind temperaturabhängig. Nachfolgend wird auf die Temperaturabhängkeit elektrischer Widerstände eingegangen.

Kaltleiter (PTC-Widerstände) besitzen bei niedriger Temperatur einen geringeren elektrischen Widerstand. Dieser erhöht sich bei steigender Temperatur. Sie besitzen einen positiven Temperaturkoeffizienten. Heißleiter (NTC-Widerstände) hingegen verfügen bei hohen Temperaturen über einen geringeren elektrischen Widerstand. Ihre Leitfähigkeit nimmt hierbei zu. Sie verfügen über einen negativen Temperaturkoeffizienten.

Durch den Temperaturkoeffizient wird die relative Änderung einer bestimmten physikalischen Größe (in diesem Fall der elektrische Widerstand) beschrieben, wenn sich diese hinsichtlich einer festgelegten Bezugstemperatur (Raumtemperatur) ändert. Widerstände wie beispielsweise Heißleiter oder Kaltleiter, deren Strom-Spannungs-Kennlinien im allgemeinen nicht linear verlaufen, werden als nichtlineare Widerstände bezeichnet.
 

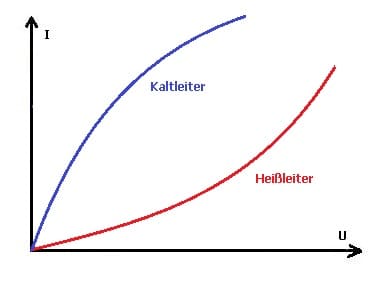
Abb. 2: Strom-Spannungs-Kennline - Heißleiter und Kaltleiter
  

 
Als Joulesche Wärme (oder Stromwärme) wird die Wärme bezeichnet, die infolge des fließenden elektrischen Stromes in einem Leiter erzeugt wird. Sie entsteht durch anhaltende Umformung elektrischer Energie. Die Umsetzung von Energie je Zeiteinheit ist eine Leistung. Die elektrische Leistung eines Verbrauchers ist im Zusammenhang mit Wärmeentwicklung stets eine Wirkleistung. Sie ergibt sich aus dem Produkt elektrischer Spannung und elektrischer Stromstärke. Die nachfolgend gezeigten Gleichungen haben Gültigkeit für Gleichstrom sowie für Effektivwerte von Wechselstrom.

Für die vom Strom im Laufe des Zeitraums t erzeugte Wärmemenge gilt das Joulesche Gesetz oder Stromwärmegesetz. Es lautet:

Q_w = P·t

bzw.

Q_w = U·I·t

mit

P = U·I
 
Q_w: erzeugte Wärmemenge [J]
P: Elektrische Leistung [W]
t: Dauer [s]
U: Spannung [V]
I: Strom [A]
 
 

 
Nachfolgend aufgeführt ist eine Tabelle für Werte des spezifischen elektrischen Widerstands einiger Stoffe.
 

 

Stoff	Spezifischer elektrischer Widerstand in [Ω·mm2/m]
Aktinium	0,027
Bakelit	1014
Barium	0,4
Benzol	1015 ... 1016
Bernstein	> 1016
Beryllium	0,075
Bismut	1,17
Blei	0,208
Beryllium	9,32
Blei	7,42
Bronze	0,0208
Cadmium	0,076
Caesium	0,2
Calcium	0,047
Celluloid	108 ... 1010
Chrom	0,15
Cobalt	0,057
Eisen	0,1
Flussstahl	0,13
Galalith	1014
Germanium	890
Glas	> 1011
Glimmer	1013 ... 1015
Gold	0,022
Graphit	8
Gusseisen	1
Hartgummi	1013 ... 1016
Holz, trocken	109 ... 1013
Iridium	0,053
Kalium	0,072
Kautschuk	6·1014
Kohlenstoff	35,315
Konstantan	0,5
Kupfer	0,0172
Magnesium	0,044
Manganin	0,43
Marmor	107 ... 108
Messing	0,75
Molybdän	0,054
Natrium	0,046
Neusilber	0,3
Nickel	0,087
Osmium	0,105
Palladium	0,11
Papier	1015 ... 1016
Petroleum	1010 ... 1012
Platin	0,107
Plexiglas	1013
Polyethylen	1010 ... 1013
Polystyrol	1015 ... 1016
Porzellan	5·1012
PVC	< 1013
Quarzglas	5·1016
Quecksilber	0,96
Rhodium	0,047
Schiefer	106
Silber	0,016
Silicium	1,2·107
Tantal	0,13
Titan	0,5
Uran	0,32
Vaseline	1010 ... 1013
Vulkanfiber	1010 ... 1011
Wasser, destilliert	104 ... 4·104
Wolfram	0,055
Zink	0,061
Zinn	0,11
Zirkonium	0,41

   

 

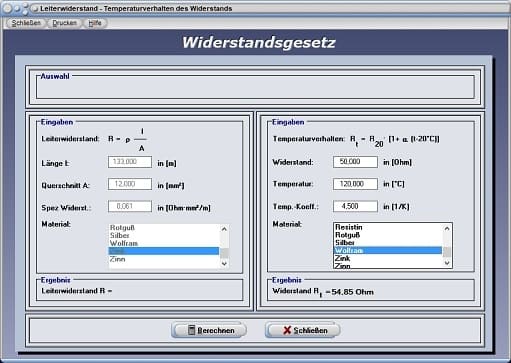
Widerstandsgesetz - Abbildung 3


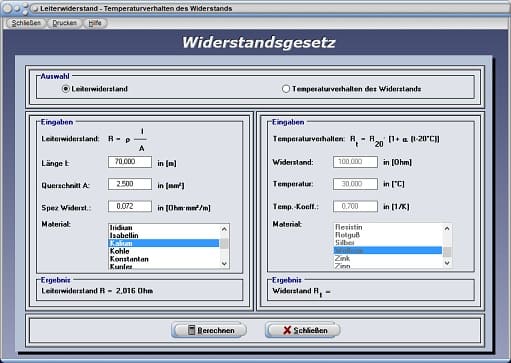
Widerstandsgesetz - Abbildung 4

 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit. 
 

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.

 

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Spezifischer Widerstand zu finden.
 

 

Lissajousche Figuren - Reihen- und Parallelschaltung - Widerstände im Wechselstromkreis - Messbrücke -  Kondensator Ladung - Entladung - Kondensator - Kapazitäten - Plattenkondensator - Transformator - Schwingungsüberlagerung - RC-Kreis - RL-Kreis - RLC-Kreis - Resonanz - Wechselstromkreis
 

    

Unterprogramm Widerstandsgesetz
 

 

PhysProf 1.1 - Unterprogramm RLC-Kreis
 

MathProf 5.0 - Unterprogramm Kurven in Parameterform
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

 

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

 
 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---