PhysProf - Widerstand - Wechselstromkreis - Blindleitwert - Leitwert
Fachthema: Widerstände im Wechselstromkreis
PhysProf - Elektrizitätslehre - Eine Software zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen zur Unterstützung des Unterrichts naturwissenschaftlicher Fächer sowie für alle die sich für Physik interessieren.
Online-Hilfe für das Modul
zum Themengebiet Widerstände im Wechselstromkreis bei
Reihenschaltung und Parallelschaltung von Widerstand, Spule und Kondensator. Die Darstellung der entsprechenden Zusammenhänge erfolgt im Zeigerdiagramm.
Dieses Unterprogramm ermöglicht die Durchführung der Steuerung entsprechender Abläufe zur Echtzeit und bietet die Möglichkeit, die Einflüsse relevanter Größen interaktiv zu untersuchen.
Es unterstützt dabei, ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.
Auch eignet es sich unter anderem als Ergänzung im Leistungskurs Physik (LK Physik) der Oberstufe am Gymnasium und kann zudem als Begleiter zum Unterricht sowie zur Erweiterung des bereits erlangten Fachwissens zu verschiedenen anderen Themengebieten zum Einsatz kommen.
Weitere relevante Seiten zu diesem Programm
Themen und Stichworte zu diesem Modul: |
 |  |
Widerstände im Wechselstromkreis
Das Unterprogramm [Elektrotechnik] - [Widerstände im Wechselstromkreis] bietet die Möglichkeit Berechnungen mit Wechselstromwiderständen unter Zuhilfenahme der Darstellung von Zeigerdiagrammen durchzuführen.
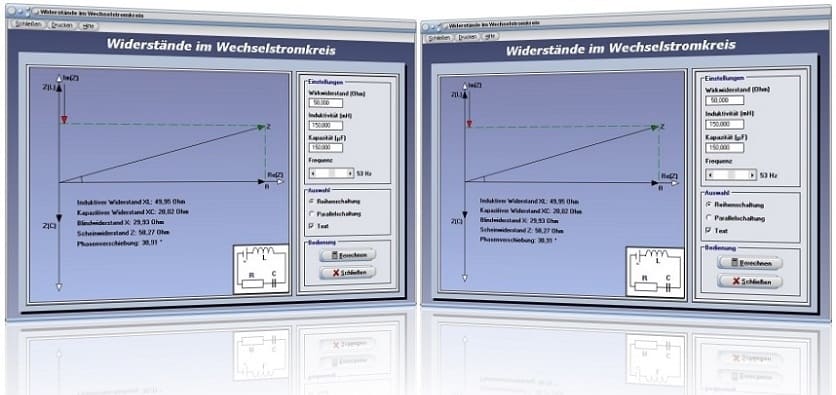
Modul Widerstände im Wechselstromkreis
Ein Wechselstromkreis unterscheidet sich von einem Gleichstromkreis vor allem durch die Tatsache, dass Stromstärke und Spannungen Funktionen der Zeit sind und sich periodisch ändern. Als Wechselspannung bzw. sinusförmige Wechselspannung wird eine Spannung bezeichnet, deren Polarität sich regelmäßig verändert. Ihr zeitlicher Mittelwert ist stets Null. Befinden sich im Wechselstromkreis außer Ohmschen Widerständen noch Induktivitäten oder Kapazitäten, so erreichen Spannung und Stromstärke nicht mehr zeitgleich ihre Maximalwerte.
Der Ohmsche Widerstand ist im Gleich- und Wechselstromkreis gleich groß, er wird bei Wechselstromkreisen als Wirkwiderstand bezeichnet. In Wechselstromkreisen treten neben dem Wirkwiderstand zusätzlich sogenannte Blindwiderstände auf. Diese verwandeln keine elektrische Energie in Wärme. Die geometrische Summe von Blind- und Wirkwiderstand heißt Scheinwiderstand.
Widerstände dieser Art lassen sich unter der Verwendung komplexer Zahlen berechnen und grafisch in der Gaußschen Zahlenebene darstellen. Diese Art der Darstellung wird als Zeigerdiagramm (Zeigerbild) bezeichnet. Durch eine vektorielle Addition der drei komplexen Zahlen für die einzelnen Widerstände kann der Scheinwiderstand ermittelt werden. Der Blindwiderstand wird hierbei als der imaginäre Teil des Scheinwiderstands ausgegeben. Die Phasenverschiebung wird durch den Winkel zwischen Scheinwiderstand und der reellen Achse beschrieben.
Im Folgenden wird auf die Grundlagen sowie wichtige Kenngrößen der Wechselstromtechnik eingegangen.
I - Reihenschaltung
Widerstände im Wechselstromkreis - Reihenschaltung - Abbildung 1
Widerstände im Wechselstromkreis - Reihenschaltung - Abbildung 2
Für den Gesamtwiderstand Z, welcher auch als Scheinwiderstand bezeichnet wird, gilt bei einer Reihenschaltung von Wechselstromwiderständen:
Mit
und
ergibt sich:
Der Blindleitwert ist der Imaginärteil des komplexen Leitwerts. Der Blindwiderstand ist definiert mit:
Für die Phasenverschiebung zwischen Stromstärke und Spannung gilt:
R: Ohmscher Widerstand (Wirkwiderstand bzw. Resistanz) [Ω]
XL: Induktiver Widerstand [Ω]
XC: Kapazitiver Widerstand [Ω]
L: Induktivität [H]
C: Kapazität [F]
f: Frequenz [1/s]
ω: Kreisfrequenz (ω = 2πf) [1/s]
φ: Phasenverschiebung [rad]
Z: Gesamtwiderstand (Scheinwiderstand bzw. Impedanz) [Ω]
II - Parallelschaltung
Widerstände im Wechselstromkreis - Parallelschaltung - Abbildung 1
Widerstände im Wechselstromkreis - Parallelschaltung - Abbildung 2
Der Gesamtleitwert 1/Z wird auch als Scheinleitwert Y bezeichnet. Als Admittanz wird der komplexe Leitwert in einem Wechselstromkreis bezeichnet. Der Betrag der Admittanz ist der Scheinleitwert Y. Für den Scheinleitwert gilt bei einer Parallelschaltung von Wechselstromwiderständen:
Mit
und
ergibt sich:
Der Blindleitwert ist definiert mit:
Für die Phasenverschiebung zwischen Stromstärke und Spannung gilt:
R: Ohmscher Widerstand (Wirkwiderstand) [Ω]
XL: Induktiver Widerstand [Ω]
XC: Kapazitiver Widerstand [Ω]
L: Induktivität [H]
C: Kapazität [F]
f: Frequenz [1/s]
ω: Kreisfrequenz (ω = 2πf) [1/s]
φ: Phasenverschiebung [rad]
X: Blindwiderstand [Ω]
B: Blindleitwert [S]
Z: Gesamtwiderstand (Scheinwiderstand bzw. Impedanz) [Ω]
Induktiver Widerstand - Kapazitiver Widerstand
Induktiver Widerstand:
In jedem Wechselstromkreis, der eine Induktivität L besitzt, existiert ein Wechselstromwiderstand, der als induktiver Widerstand XL bezeichnet wird. Bei einem induktiven Widerstand wird elektrische Energie in magnetische Energie der Spule umgewandelt. Dies geschieht ebenfalls konträr.
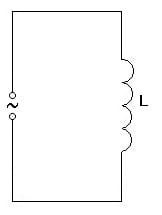
Abb 1.: Induktiver Widerstand - Schaltbild
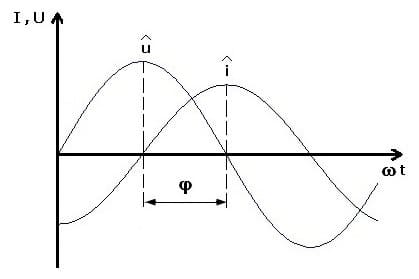
Abb 2.: Induktiver Widerstand - Phasendiagramm
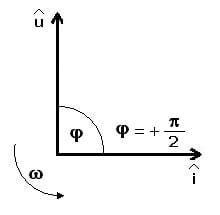
Abb 3.: Induktiver Widerstand - Zeigerdiagramm
Eine Induktivität wirkt auf die Stromänderung stets verzögernd. In einem Wechselstromkreis mit reiner Induktivität eilt die Spannung dem Strom um π/2 voraus. Zwischen Spannung und Strom existiert in diesem Fall ein Phasenunterschied (eine Phasenverschiebung) von π/2.
Für den induktiven Widerstand im Wechselstromkreis gilt:
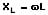
XL: Induktiver Widerstand [Ω]
L: Induktivität [H]
ω: Kreisfrequenz (ω = 2πf) [1/s]
Der Strom in einem Stromkreis mit lediglich einer Induktivität kann wie folgt berechnet werden:
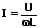
I: Strom [A]
U: Spannung [V]
L: Induktivität [H]
ω: Kreisfrequenz (ω = 2πf) [1/s]
Kapazitiver Widerstand:
In jedem Wechselstromkreis, der eine Kapazität C besitzt, existiert ein Wechselstromwiderstand, der als kapazitiver Widerstand XC bezeichnet wird. Bei einem kapazitiven Widerstand wird elektrische Energie in die Energie des elektrischen Feldes des Kondensators umgewandelt. Dies geschieht ebenfalls konträr.
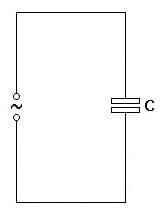
Abb 1.: Kapazitiver Widerstand - Schaltbild
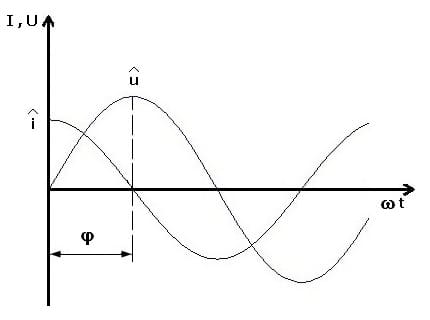
Abb 2.: Kapazitiver Widerstand - Phasendiagramm
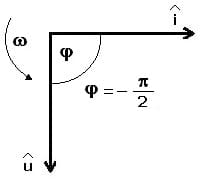
Abb 3.: Kapazitiver Widerstand - Zeigerdiagramm
Eine Kapazität wirkt auf die Spannung stets verzögernd. In einem Wechselstromkreis mit reiner Kapazität eilt der Strom der Spannung um π/2 voraus. Zwischen Spannung und Strom existiert in diesem Fall ein Phasenunterschied (eine Phasenverschiebung) von -π/2.
Für den kapazitiven Widerstand im Wechselstromkreis gilt:
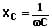
XC: Kapazitiver Widerstand [Ω]
C: Kapazität [F]
ω: Kreisfrequenz (ω = 2πf) [1/s]
Der Strom in einem Stromkreis mit lediglich einem kapazitiven Widerstand kann wie folgt berechnet werden:
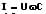
I: Strom [A]
U: Spannung [V]
C: Kapazität [F]
ω: Kreisfrequenz (ω = 2πf) [1/s]
Blindwiderstand
Der Blindwiderstand begrenzt den Aufbau einer sinusförmigen Wechselspannung und verursacht eine Phasenverschiebung zwischen Spannung und Stromstärke. Sind Spulen und Kondensatoren gemeinsam in einem Wechselstromkreis vorhanden, so gelten die nachfolgend aufgeführten Regeln:
1. Reihenschaltung:
Kondensator und Spule (L und C) sind in Reihe geschaltet:
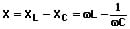
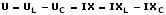
2. Parallelschaltung:
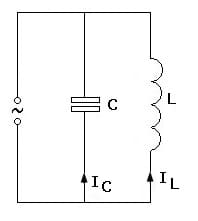
Kondensator und Spule (L und C) sind parallelgeschaltet:
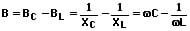
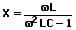
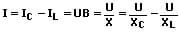
U: Gesamtspannung [V]
I: Gesamtstromstärke [A]
UL: Spannung am induktiven Widerstand [V]
UC: Spannung am kapazitiven Widerstand [V]
IL: Stromstärke durch induktiven Widerstand [A]
IC: Stromstärke durch kapazitiven Widerstand [A]
XL: Induktiver Widerstand [Ω]
XC: Kapazitiver Widerstand [Ω]
X: Gesamter Blindwiderstand [Ω]
B: Blindleitwert = 1/X [1/Ω]
Scheinwiderstand (Impedanz)
Der Scheinwiderstand (die Impedanz bzw. der Wechselstromwiderstand) bildet sich aus ohmschem Widerstand und Blindwiderstand. Sind Scheinwiderstand und ohmscher Widerstand gemeinsam in einem Wechselstromkreis vorhanden, so gelten die nachfolgend aufgeführten Regeln:
1. Reihenschaltung:
Scheinwiderstand und ohmscher Widerstand (X und R) sind in Reihe geschaltet:
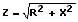
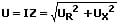
2. Parallelschaltung:
Scheinwiderstand und ohmscher Widerstand (X und R) sind parallelgeschaltet:
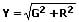
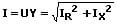
U: Gesamtspannung [V]
I: Gesamtstromstärke [A]
Z: Scheinwiderstand [Ω]
R: Ohmscher Widerstand (Wirkwiderstand) [Ω]
X: Blindwiderstand [Ω]
S: Scheinleitwert = 1/Z [1/Ω]
G: Wirkleitwert = 1/R [1/Ω]
B: Blindleitwert = 1/X [1/Ω]
Phasenverschiebung - Phasendifferenz
Der Betrag der Phasendifferenz die durch induktiven und kapazitiven Widerstand in einem Wechselstromkreis verursacht wird beträgt π/2 bzw. -π/2. Eine Phasendifferenz wird auch als Phasenunterschied bezeichnet.
Da jedoch nahezu alle Stromkreise zudem einen ohmschen Widerstand (einen Wirkwiderstand bzw. Resistanz) besitzen, entsteht in diesen Fällen eine Phasenverschiebung, die sich zwischen den Werten -π/2 und π/2 für den Phasenwinkel bewegt. Der Phasenwinkel (die Phase) beschreibt die aktuelle Position dieses periodischen Vorgangs. Die Phasenverschiebung kann mit Hilfe der nachfolgend dargestellten Zeigerdiagramme ermittelt, bzw. errechnet werden:
1. Reihenschaltung:
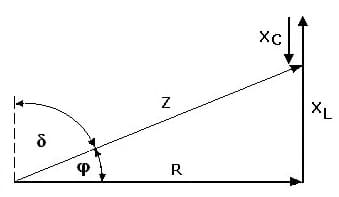
Widerstand, Kondensator und Spule (R, L und C) sind in Reihe geschaltet:
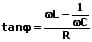
2. Parallelschaltung:
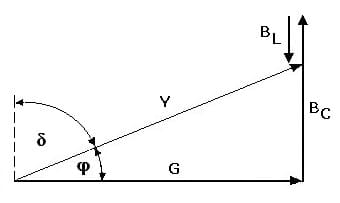
Widerstand, Kondensator und Spule (R, L und C) sind parallelgeschaltet:
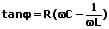
φ: Phasenverschiebung [rad]
ω: Kreisfrequenz (ω = 2πf) [1/s]
R: Ohmscher Widerstand (Wirkwiderstand bzw. Resistanz) [Ω]
L: Induktivität [H]
C: Kapazität [F]
Programmbedienung
Dieses Modul ermöglicht es, Untersuchungen zu diesem Fachthema durchführen und sich Darstellungen im Zeigerdiagramm für die Reihen- und Parallelschaltung von Ohmschen Widerständen, Kondensatoren und Spulen ausgeben zu lassen.
Wählen Sie hierfür zunächst die Schaltungsart durch die Aktivierung des entsprechenden Kontrollschalters Reihenschaltung bzw. Parallelschaltung aus. Geben Sie daraufhin die für die Durchführung der Berechnung benötigten Werte für den Wirkwiderstand, die Induktivität und die Kapazität ein.
Legen Sie durch die Positionierung des zur Verfügung stehenden Rollbalkens die relevante Frequenz fest und bedienen Sie hierauf die Schaltfläche Berechnen.
Unmittelbar daraufhin erhalten Sie alle errechneten Ergebnisse und eine Aktualisierung der Darstellung. Mit Hilfe des zur Verfügung stehenden Kontrollkästchens Text können Sie festlegen, ob die numerischen Ergebnisse in der Grafik angezeigt werden sollen.
Schwingkreis - Resonanzkreis (LC-Kreis) - Resonanz
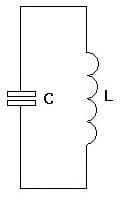
Als elektrischer Schwingkreis (Resonanzkreis) wird eine resonanzfähige elektrische Schaltung bezeichnet, die sich aus einer Spule und einem Kondensator zusammensetzt. Bei diesem LC-Schwingkreis (LC-Glied) erfolgt ein periodisch ablaufender Energieaustausch zwischen dem magnetischen Feld der Spule und dem elektrischen Feld des Kondensators. Hierduch findet ein stetiger Wechsel zwischen hoher Stromstärke und hoher Spannung statt. Die hierbei vorliegende Resonanzfrequenz kann mit Hilfe der Thomson-Gleichung ermittelt werden. Die Thomsonsche Schwingungsgleichung lautet wie folgt:
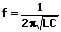
bzw:
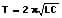
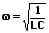
L: Induktivität [H]
C: Kapazität [F]
ω: Kreisfrequenz (ω = 2πf) [1/s]
f: Frequenz der Wechselspannung [1/s]
T: Periodendauer [s]
Hinsichtlich der Resonanz eines Schwingkreises sind zwei grundlegende Fälle zu unterscheiden. Dies sind:
1. Parallelresonanz (Stromresonanz):
Parallelresonanz (Stromresonanz) liegt vor, wenn Induktivität (Spule) und Kapazität (Kondensator) parallelgeschaltet sind. Hierbei ergibt sich ein Minimum an Strom und die Teilströme durch die Blindwiderstände sind größer als der Gesamtstrom.
2. Reihenresonanz (Spannungresonanz):
Reihenresonanz (Spannungresonanz) liegt vor, wenn Induktivität (Spule) und Kapazität (Kondensator) in Reihe geschaltet sind. Hierbei ergibt sich ein Maximum an Strom und die Teilspannungen über den Blindwiderständen sind größer als die Gesamtspannung.
Leistung - Scheinleistung - Wirkleistung - Blindleistung - Leistungsfaktor - Nennleistung
Leistung im Wechselstromkreis
Verursacht durch die Phasenverschiebung zwischen Strom und Spannung der Induktivität bzw. der Kapazität in einem Wechselstromkreis tritt ein soganannter Blindanteil dieser beiden Größen auf. Der Blindanteil der Leistung in einem derartigen System wird als Blindleistung Q, der Wirkanteil dessen als Wirkleistung P bezeichnet.
Die erbrachte Gesamtleistung eines Wechselstromkreises trägt die Bezeichnung Scheinleistung S. Zwischen der Wirkleistung P und der Blindleistung Q liegt eine Phasenverschiebung mit einem Winkel von 90° vor.
Der Wirkleistungsfaktor (Leistungsfaktor) beschreibt das Verhältnis zwischen Wirkleistung P und Scheinleistung S. Das Verhältnis zwischen Blindleistung Q und Scheinleistung S wird als Blindleistungsfaktor bezeichnet.
Für die oben beschriebenen Leistungen in einem Wechselstromkreis gelten die nachfolgend aufgeführten Gesetzmäßigkeiten:
Scheinleistung:
S = U · I
bzw:
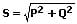
Wirkleistung:
P = U · I · cos φ = S · cos φ
Blindleistung:
Q= U · I · sin φ = S · sin φ
Wirkleistungsfaktor:
cos φ = P/S
Blindleistungsfaktor:
sin φ = P/S
S: Scheinleistung [VA]
P: Wirkleistung [W]
Q: Blindleistung [var]
cos φ: Wirkleistungsfaktor
sin φ: Blindleistungsfaktor
Als Nennleistung einer elektrischen Anlage, oder eines elektrischen Geräts (Verbrauchers) wird eine von dessen Hersteller angegebene Leistung bezeichnet, mit der dieses betrieben werden kann bzw. wird hiermit die von diesem Gerät abgegebene Leistung beschrieben.
Als Verlustleistung wird die Abweichung bezeichnet, die zwischen aufgenommener Leistung und abgegebener Leistung eines Gerätes oder Prozesses resultiert. Sie tritt unter anderem in elektrischen Netzen infolge des Widerstands elektrischer Leiter (Leitungswiderstand) auf. Verluste dieser Art werden als Leitungsverluste bezeichnet. Allgemein kann die Verlustleistung eines Leiters wie folgt berechnet werden:
Pv = I²·R
Sie erhöht sich innerhalb einer Leitung mit dem Quadrat des Stroms der durch sie fließt.
Pv: Verlustleistung des Leiters [W]
I: Strom der durch den Leiter fließt [A]
R: Widerstand des Leiters (Leitungswiderstand) [Ω]
Blindstrom - Blindleistungskompensation - Blindstromkompensation
Blindstrom ist der Anteil des Stroms, der zwischen dem Generator des Elektrizitätswerks und dem Verbraucher lediglich periodisch hin und her wandert. Im Gegensatz zu Wirkstrom bezeichnet Blindstrom einen Stromanteil im Wechselstromnetz, der keine Wirkleistung überträgt, das Stromnetz jedoch belastet.
Der Begriff Kompensation bedeutet Ausgleich. Die Blindleistungskompensation oder Blindstromkompensation wird in Wechselstromnetzen eingesetzt, um den Blindstrom von elektrischen Verbrauchern zu reduzieren. Es wird unterschieden zwischen induktiven Blindströmen und kapazitiven Blindströmen. Induktive Blindströme entstehen u.a. durch elektromagnetische Effekte in Spulen von Elektromotoren. Kapazitiver Blindstrom wird in Kondensatoren erzeugt.
Um den induktiven Blindstrom in einer Anlage auszugleichen (zu kompensieren) werden Verbrauchern Kondensatoren der jeweils angemessenen Leistung parallelgeschaltet.
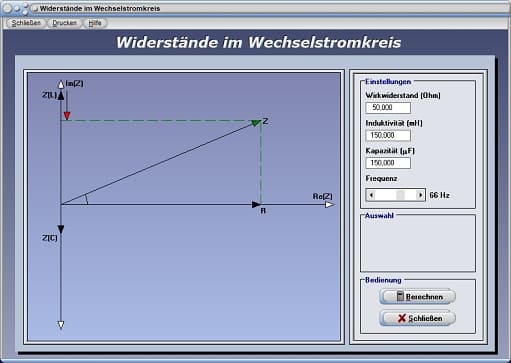
Widerstände im Wechselstromkreis - Reihenschaltung - Abbildung 3
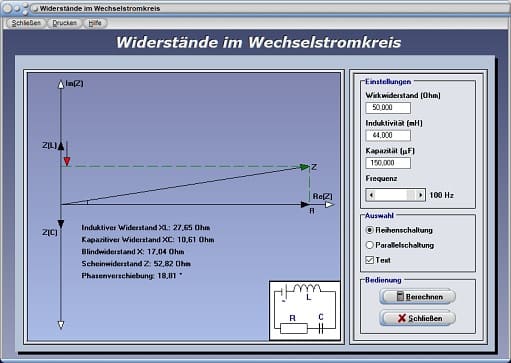
Widerstände im Wechselstromkreis - Reihenschaltung - Abbildung 4
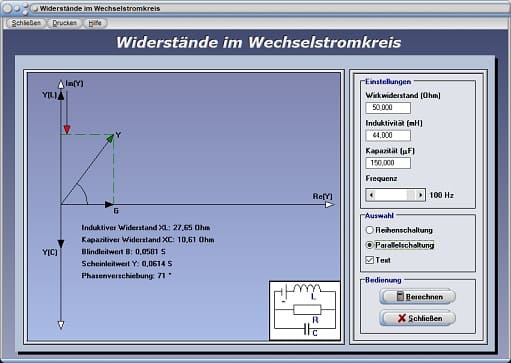
Widerstände im Wechselstromkreis - Parallelschaltung - Abbildung 3
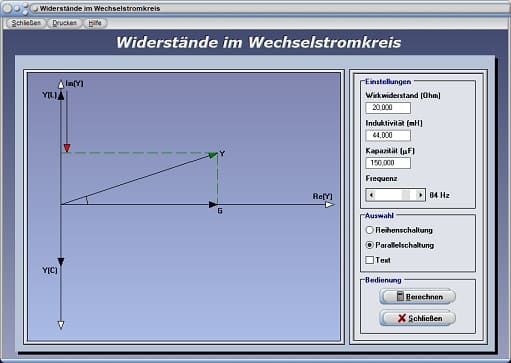
Widerstände im Wechselstromkreis - Parallelschaltung - Abbildung 4
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.
Wikipedia - Wechselstrom
Wikipedia - Elektrischer Widerstand
Wikipedia - Blindwiderstand
Wikipedia - Wirkwiderstand
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
Lissajousche Figuren - Reihen- und Parallelschaltung - Messbrücke - Widerstandsgesetz - Kondensator Ladung - Entladung - Kondensator - Kapazitäten - Plattenkondensator - Transformator - Schwingungsüberlagerung - RC-Kreis - RL-Kreis - RLC-Kreis - Resonanz - Wechselstromkreis
Unterprogramm Widerstände im Wechselstromkreis
PhysProf 1.1 - Unterprogramm RLC-Kreis
MathProf 5.0 - Unterprogramm Kurven in Parameterform
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Physik interaktiv
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
Eine Übersicht aller in MathProf 5.0 zur Verfügung stehender Programmteile finden Sie im MathProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
