PhysProf - Kräftezerlegung - Kräfte - Resultierende - Zerlegung
Fachthemen: Kraft - Kräftezerlegung - Kräfteparallelogramm - Kräftedreieck
PhysProf - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.
Online-Hilfe für das Modul
zur Durchführung von Vektoradditionen.
Dieses kleine Modul bietet die Möglichkeit Sachverhalte zu untersuchen, die bei der Durchführung einer Addition bzw. einer Subtraktion von Vektoren gelten. Es ermöglicht zudem die Zusammenhänge bei der Bildung eines Kräfteparallelogramms zu analysieren.
Die entsprechenden Komponenten können durch Werteingaben, wie auch mittels der Durchführung von Mausoperationen definiert werden.
Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.
Themen und Stichworte zu diesem Modul: |
 |  |
Kräfteparallelogramm
Der Menüpunkt [Allgemeines] - [Vektoren] - [Vektoraddition] stellt ein kleines Modul zur Verfügung, mit welchem das Prinzip der Durchführung einer Vektoraddition bzw. -subtraktion untersucht werden kann.
Vektoraddition
Vektorsubtraktion
Vektoren sind Größen, welche durch die Angabe der Maßzahl und der Richtung vollständig beschrieben sind. Diese werden in symbolischer Weise als Pfeil dargestellt. Ein physikalischer Vektor besteht durch die Angabe einer Maßzahl und einer Einheit.
Darstellung von Kräften:
Kräfte sind gerichtete Größen (vektorielle Größen), die von ihrer Richtung, ihrem Betrag sowie ihrem Angriffspunkt abhängig sind. Bei derer grafischen Darstellung entspricht die Richtung des hierfür verwendeten Pfeils der Richtung der wirkenden Kraft. Der Anfangspunkt des Pfeils entspricht dem Angriffspunkt der Kraft. Der Betrag der wirkenden Kraft wird durch die Länge des Pfeils gekennzeichnet.
Bei einem zentralen Kräftesystem handelt es sich um eine Gruppe von Kräften, deren Wirkungslinien durch einen Punkt P verlaufen. Im vorliegenden Fall handelt es sich um das einfachste System dieser Art, bei welchem zwei wirkende Kräfte die in einer Ebene liegen und ihren Ursprung im Zentrum des Koordinatensystems besitzen. Von einem allgemeinen Kräftesystem wird gesprochen, wenn kein gemeinsamer Angriffspunkt aller wirkenden Kräfte vorliegt.
Ein Kräfteparallelogramm dient der zeichnerischen, zweidimensionalen grafischen und geometrischen Analyse von Kräften. Grundlage ist das Gesetz der Mechanik, welches besagt, dass je zwei an einem selben Punkt angreifende Kräfte durch eine einzige Kraft ersetzt werden können.
Dieses kleine Unterprogramm ermöglicht die geometrische (zeichnerische) Konstruktion des Kräfteparallelogramms unter Anwendung der Parallelogrammregel. Hierbei wird aus den Teilkräften F1 und F2 ein Summenvektor bzw. ein Differenzvektor Fres erzeugt. Diese resultierende Kraft (Gesamtkraft, Ersatzkraft) besitzt die selbe Wirksamkeit wie die beiden Einzelkräfte.
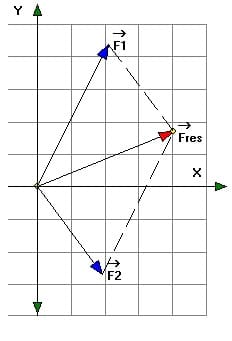
Für die beiden Kräfte F1 und F2 gilt:
Fxres = F1x + F2x
Fyres = F1y + F2y
Fres = F1 + F2
Der Betrag der resultierenden Kraft Fres berechnet sich wie folgt:
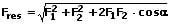
Als Wirklinie (Wirkungslinie) wird die Gerade bezeichnet, welche die Lage einer Kraft in der Ebene bzw. im Raum angibt. Mittels der Angabe ihres Angriffspunkts, ihres Betrags, sowie ihrer Richtung wird ein Kraftvektor beschrieben.
Bei der Durchführung einer Kräftezerlegung wird mindestens eine einzelne Kraft in wenigstens zwei Teilkräfte zerlegt, deren Wirkungsrichtungen unterschiedlich sind.
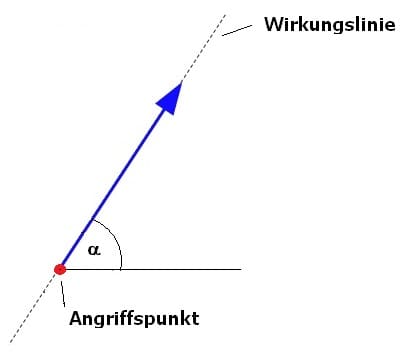
Als Angriffspunkt wird derjenige Punkt angegeben, an dem eine Kraft angreift.
Als zentrales (ebenes) Kräftesystem wird eine Kräftegruppe benannt, deren Kräfte in einer Ebene liegen und sich alle ihre Wirkungslinien in einem Punkt treffen.
Als vektorielle Größe (gerichtete Größe) wird eine physikalische Größe bezeichnet, der neben ihrem Zahlenwert auch eine Richtung zugeordnet ist.
Ein Kraftvektor ist ein gebundener Vektor mit gegebener Richtung, Länge und gegebenem Angriffspunkt.
Unter einer Kräfteaddition wird die Durchführung der Vektoraddition einzelner Teilkräfte verstanden, um die daraus resultierende Gesamtkraft (Ersatzkraft) zu ermitteln.
Der Kraftvektor ist ein Vektor, der über einen Angriffspunkt verfügt und in Richtung sowie Länge eindeutig bestimmt ist. In der Ebene besitzt er zwei Komponenten, im Raum sind dies drei.
Programmbedienung
Mittels der Aktivierung des Kontrollschalters Addition bzw. Subtraktion kann festgelegt werden, ob eine Addition oder eine Subtraktion der Kraftkomponenten der beiden Einzelvektoren durchgeführt wird. Durch das Anfassen der Pfeilspitze eines Vektors mit Hilfe der Maus und einer Verschiebung des Cursors, bei gedrückt gehaltener linker Maustaste, kann der Pfeil in die gewünschte Position gebracht werden.
Alle Werte und Ergebnisse werden bei der Durchführung von Mausoperationen (auch in den Eingabefeldern) stets aktualisiert. Alternativ dazu können dargestellten Vektoren, durch die Eingabe von Zahlenwerten in die entsprechenden Felder, exakte Komponentenwerte zugewiesen werden. Durch einen Klick auf die Schaltfläche Übernehmen, werden die eingegebenen Werte verwendet. Das Kontrollkästchen Mausfang ermöglicht bei dessen Aktivierung bzw. Deaktivierung das Ein- bzw. Ausschalten eines markierten Mausfangbereichs.
Das Programm gibt die Komponentenwerte sowie den Betrag des resultierenden Vektors Fres aus.
Beispiel
Werden bei der Durchführung einer Vektoraddition der beiden Kräfte F1 + F2 für die Komponenten des Kraftvektors F1 die Werte F1x = -4 und F1y = 5 sowie für die Kraftkomponenten des Vektors F2 die Werte F2x = -3 und F2y = -4 in den dafür vorgesehenen Eingabefeldern festgelegt, so ermittelt das Programm für die Komponenten des resultierenden Kraftvektors nach einer Bedienung der Schaltfläche Berechnen die Werte Fxres = -7 und Fyres = -1. Zudem wird für den Betrag des resultierenden Vektors der Wert Fres = 7,071 N ausgegeben.
Werden diese Eingabewerte beibehalten und wird hierauf der Kontrollschalter Subtraktion gewählt, so gibt das Programm für die durchgeführte Subtraktion der beiden Vektoren F1 - F2 die Werte Fxres = -1 und Fyres = -9 aus. Der Betrag des resultierenden Vektors besitzt den Wert Fres = 9,055 N.
Kräftedreieck
In einem Kräftedreieck erfolgt die Verschiebung des Angriffpunkts des Vektors F2 an das Ende des Vektors F1.
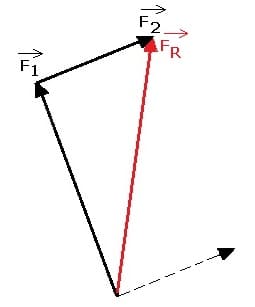
Hierauf kann aus dieser Anordnung, wie in obiger Abbildung dargestellt, die Resultierende der beiden Vektoren gebildet werden. Dies erfolgt durch die Verbindung des Angriffspunkts des Vektors F1 mit dem Endpunkt des Vektors F2. Der gestrichelt dargestellte Pfeil beschreibt hierbei die Ursprungslage (Ausgangsposition) des Vektors F2 vor dessen Verschiebung.
Kraftarten
Hinsichtlich der Einteilung von Kräften gemäß ihrer Art kann unterschieden werden zwischen den nachfolgend aufgeführten Kraftarten:
Fundamentale Kräfte:
Fundamentale Kräfte entscheiden darüber, wie sich Materie verhält und in welcher Art Wechselwirkungen auftreten und sie bestimmendas Erscheinungsbild der Materie die uns umgibt. Dies sind die magnetische Kraft, die elektrische Kraft, die Schwerkraft und die Atomkraft.
Abgeleitete Kräfte:
Kräfte dieser Art sind von den Fundamentalkräften abgeleitete Kräfte. Besipiele für derartige Kräfte sind die Federkraft, die Reibungskraft, die Auftriebskraft, die Normalkraft sowie die Radialkraft.
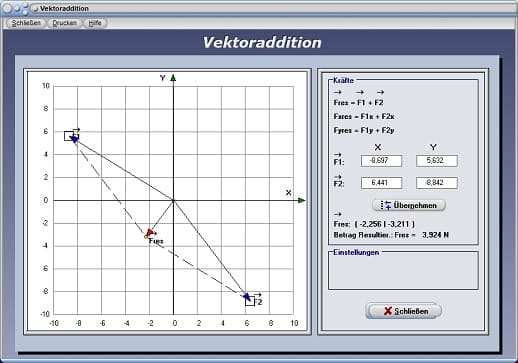
Vektoraddition - Abb. 1
Vektoraddition - Abb. 2
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen oder deren Frageworte die Wörter Welche?, Welcher?, Welches? bzw. Wodurch? sind, beantwortet werden und zugrunde liegende Sachverhalte können einfach erklärt werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Notizen - Taschenrechner - Fachbegriffe Deutsch - Englisch - Materialkonstanten - Physikalische Größen - Maßeinheiten - Naturkonstanten - Physiker - Nobelpreisträger - Periodensystem der Elemente - Messwertreihen - Statistische Messwertanalyse - Zusammenhang von Messwerten - Regressionsanalyse - Vektorprojektion
Videos zu einigen in PhysProf implementierten Modulen sind auf Youtube unter den folgenden Adressen abrufbar:
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
Unterprogramm Vektoraddition
PhysProf 1.1 - Unterprogramm RLC-Kreis
MathProf 5.0 - Unterprogramm Kurven in Parameterform
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Physik interaktiv
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
Eine Übersicht aller in MathProf 5.0 zur Verfügung stehender Programmteile finden Sie im MathProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
