PhysProf - Stromkreis - Reihen- und Parallelschaltung - Kirchhoffsche Gesetze

Fachthemen: Reihenschaltung - Parallelschaltung - Stromkreis - Elektrische Arbeit - Elektrische Leistung - Kirchhoffsche Gesetze
PhysProf - Grundlagen der Elektrotechnik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle Anwender technischer Berufe die sich für Physik interessieren.

Online-Hilfe für das Modul
zur Untersuchung geltender Gesetzmäßigkeiten bei Reihenschaltungen und Parallelschaltungen im Gleichstromkreis und im Wechselstromkreis.
Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden physikalischen Sachverhalte und eignet sich zudem als Begleitung zu Versuchen im Physikunterricht.
Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.

Weitere relevante Seiten zu diesem Programm

Themen und Stichworte zu diesem Modul: |
 |  |
Reihenschaltung und Parallelschaltung - Kirchhoffsche Gesetze
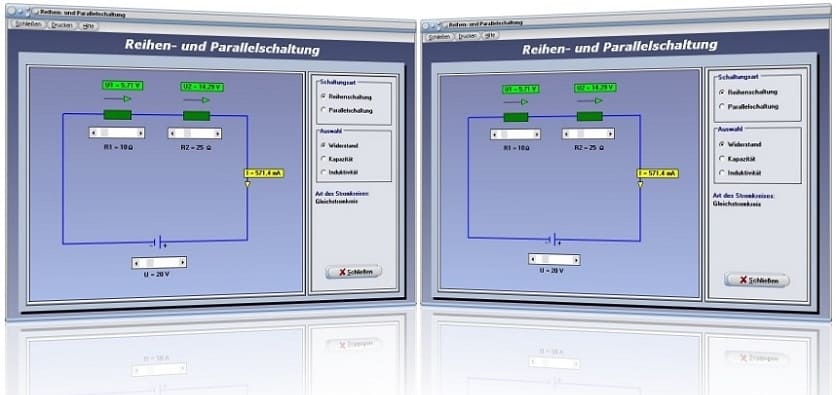
Modul Reihenschaltung und Parallelschaltung
Das Unterprogramm [Elektrotechnik] - [Reihen- und Parallelschaltung] widmet sich den Sachverhalten, welche bei grundlegenden Schaltungen im Gleichstromkreis und Wechselstromkreis zugegen sind.
Grundlagen - Grundlegendes
Elektrischer Strom:
Der in einem elektrischen Leiter fließende Strom (elektrischer Strom) besteht aus elektrischen Ladungsträgern (Elektronen) die sich in diesem fortbewegen. Diese Ladungsträger werden als freie Elektronen bezeichnet. Der Transport dieser hat unter anderem die Temperaturerhöhung des Leiters sowie die magnetische Wirkung zur Folge.
Stromrichtung:
Als technische Stromrichtung ist festgelegt: Der elektrische Strom fließt vom Pluspol zum Minuspol. Für die physikalische Stromrichtung gilt: Der elektrische Strom fließt vom Minuspol zum Pluspol.
Elektrische Stromstärke:
Die elektrische Stromstärke (Stromstärke) I beschreibt die Menge an elektrischer Ladung, die durch einen elektrischen Leiter, bezogen auf seine Querschnittsfläche fließt. Sie ist eine SI-Basiseinheit und wird in Ampere (A) gemessen. Je mehr elektrischer Strom innerhalb eines bestimmten Zeitraums durch den Leiter fließt, desto höher ist die Stromstärke.
Elektrische Spannung:
Die elektrische Spannung U (die Quellenspannung Uq bzw. Urspannung Ue) ist die Ursache des elektrischen Stroms und liegt an den Polen einer Spannungsquelle an. Sie beruht darauf, dass an deren Minuspol ein Elektronenüberschuss vorhanden ist und am Pluspol ein Elektonenmangel herrscht. Diese beiden Zustände bleiben bei einer Spannungsquelle stetig aufrechterhalten. Außerhalb der Spannungsquelle bewegen sich die Elektronen vom Minuspol zum Pluspol.
Eine Spannungsquelle ist ein aktiver Zweipol, der zwischen seinen Anschlussstellen eine elektrische Spannung zur Verfügung stellt. Die elektrische Spannung ist eine SI-Basiseinheit und wird in Volt (V) angegeben.
Elektrischer Stromkreis: Als elektrischer Stromkreis wird ein System elektrischer Leiter bezeichnet, welches einen geschlossenen Pfad darstellt.
Spannungsabfall:
Als Spannungsabfall wird diejenige Spannung U bezeichnet, die zwischen zwei beliebigen Punkten eines stromdurchflossenen Leiters besteht und ein Teil der Urspannung ist.
Elektrischer Widerstand:
Der elektrische Widerstand R bestimmt die Stärke des elektrischen Stroms, der bei einer bestimmten elektrischen Spannung durch einen elektrischen Leiter fließt. Der elektrische Widerstand ist eine SI-Einheit und wird in Ohm (Ω) angegeben.
Festwiderstand:
Als Festwiderstand wird ein elektronisches Bauelement bezeichnet, mit dessen Hilfe der elektrische Widerstand als physikalische Größe verwirklicht wird.
Ohmsches Gesetz (Ohmscher Widerstand):
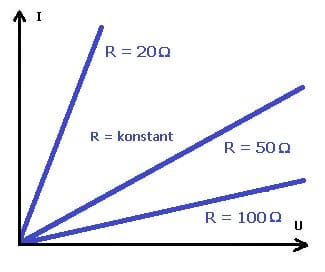
Das Ohmsche Gesetz lautet: In einem Leiter ist die Stromstärke der Spannung direkt und dem Widerstand umgekehrt proportional. Es gilt die Definitionsgleichung:
R = U/I
R: Leiterwiderstand [Ω]
U: Spannung [V]
I: Stromstärke [A]
Elektrischer Leitwert:
Der Kehrwert des elektrischen Widerstands ist der elektrische Leitwert G. Seine SI-Einheit wird in Siemens (S) angegeben. Seine Definition lautet:
G = 1/R
G: Leitwert [S]
R: Leiterwiderstand [Ω]
Elektrische Schaltungen:
Als elektrische Schaltung wird der Zusammenschluss elektrischer (elektronischer) oder elektromechanischer Einzelbauelemente zu einer funktionsgerechten Formation (Anordnung) bezeichnet.
Elektronenüberschuss - Elektronenmangel:
Besitzt ein Atom in seiner Hülle mehr negative Ladungen als positive Ladungen in seinem Kern, so herrscht ein Elektronenüberschuss und es wird als negatives Ion bezeichnet. Dieses Atom verfügt nach außen über eine negative Ladung.
Liegt hingegen ein Elektronenmangel vor, besitzt ein Atom somit in seiner Hülle weniger negative Ladungen als positive Ladungen in seinem Kern, so trägt es die Bezeichnung positives Ion. Dieses Atom ist nach außen positiv geladen.
Ohmscher Widerstand (Gleichstromwiderstand):
Als Ohmscher Widerstand (Gleichstromwiderstand) wird ein elektrischer Widerstand bezeichnet, wenn der Wert seines Widerstands unabhängig von der an ihm anliegenden Spannung und der in ihm herrschenden Stromstärke konstant bleibt. Er beschreibt die Eigenschaft des elektrischen Widerstands eines Leiters. Sein elektrischer Widerstand ist im Wechselstromkreis gleich groß wie im Gleichstromkreis.
Stromkreis:
Der Stromkreis stellt ein abgeschlossenes System elektrischer Leiter dar, die so miteinander verbunden sind, damit elektrische Ladung im Kreis transportiert werden kann. Stromkreise bestehen aus einer Strom- bzw. Spannungsquelle, einem oder mehreren Verbrauchern sowie aus Leitungen, mittels derer einzelne Komponenten (Bauteile) miteinander verbunden sind.
Bei einem Gleichstromkreis handelt es sich um einen Stromkreis, in welchem Gleichstrom fließt.
Gleichspannung:
Gleichspannung ist eine elektrische Spannung, deren Momentanwert über einen längeren Betrachtungszeitraum unverändert bleibt. Sie besitzt zu jedem Zeitpunkt den selben Betrag sowie die selbe Polarität. Elektronen bewegen sich vom Pluspol zum Minuspol der Spannungsquelle.
Gleichstrom:
Mit dem Begriff Gleichstrom wird elektrischer Strom bezeichnet, dessen Momentanwerte der Stromstärke zeitlich unverändert bleiben. Sie sind vielmehr konstant und der elektrische Strom fließt stets in die gleiche Richtung.
Gleichspannungsquelle:
Unter dem Begriff Gleichspannungsquelle wird eine Spannungsquelle verstanden, die Gleichspannung liefert und ihre Spannung zeitlich konstant hält. Sie liefert beispielsweise elektrische Energie für den Betrieb von Batterien, Akkumulatoren und Netzgeräten sowie zur Stromversorgung elektronischer Schaltungen.
Unverzweigter Stromkreis:
Als unverzeigter Stromkreis (Reihenschaltung) wird ein Stromkreis bezeichnet, in welchem durch alle Widerstände der gleiche Strom fließt. Die Gesamtspannung ist gleich der Summe aller Teilspannungen.
Verzweigter Stromkreis:
Als verzweigter Stromkreis (Parallelschaltung) wird ein Stromkreis bezeichnet, bei welchem die elektrische Spannung an allen Widerständen gleich groß ist. Der Gesamtstrom ist gleich der Summe aller Teilströme.
Nennspannung:
Mit dem Begriff Nennspannung wird diejenige Spannung bezeichnet, die ein elektrischer Verbraucher oder eine elektrische Spannungsquelle gemäß den Angaben seines Herstellers oder Lieferanten erforderlich ist, um den Normalbetrieb dieses Verbrauchers zu ermöglichen.
Gesamtwiderstand:
Der Gesamtwiderstand entspricht der Summe der Teilwiderstände einer elektrischen Schaltung.
Gesamtinduktivität:
Die Gesamtinduktivität entspricht der Summe der einzelnen Induktivitäten einer elektrischen Schaltung.
Gesamtkapazität:
Die Gesamtkapazität entspricht der Summe der einzelnen Kapazitäten einer elektrischen Schaltung.
Gesamtspannung:
Die Gesamtspannung entspricht der Summe der einzelnen Spannungen einer elektrischen Schaltung.
Gesamtstrom (Gesamtstromstärke):
Der Gesamtstrom entspricht der Summe der einzelnen Ströme einer elektrischen Schaltung.
Stromfluss:
Als Stromfluss werden die sich in in einem elektrischen Leiter fortbewegenden Elektronen bezeichnet.
Stromteiler:
Ein Stromteiler stellt eine Parallelschaltung mehrerer passiver elektrischen oder magnetischer Zweipole dar, mit Hilfe derer elektrischer Strom oder magnetischer Fluss in Teilströme (Teilflüsse) unterteilt wird.
Einfacher Stromkreis - Geschlossener Stromkreis - Offener Stromkreis
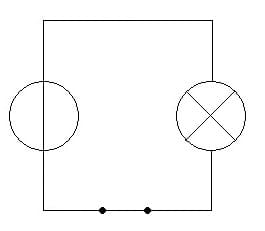
Abb. 1 - Geschlossener Stromkreis
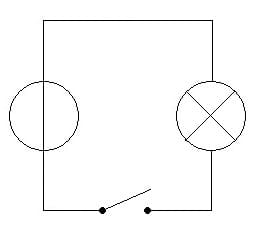
Abb. 2 - Offener Stromkreis
Stromkreislauf:
Einfache Stromkreise bestehen aus einer elektrischen Quelle (Stromquelle bzw. Spannungsquelle) sowie wenigstens einem elektrischen Gerät oder Bauteil (Stromverbraucher) die mittels elektrischer Leitungen miteinander verbunden sind.
Offener Stromkreis:
In einem offenen Stromkreis fließt kein elektrischer Strom, der Stromkreislauf ist unterbrochen. Die Umwandlung eines geschlossenen Stromkreises in einen offenen Stromkreis kann durch die beabsichtigte Unterbrechung des Stromkreislaufs mittels eines Schalters (Ein-Aus-Schaltung) erfolgen.
Geschlossener Stromkreis:
Von einem geschlossenen Stromkreis wird gesprochen, wenn innerhalb dessen elektrischer Strom fließt. In einem derartigen Stromkreis sind die entsprechenden Bauelemente in dieser Form miteinander verbunden, dass ein Fließen elektrischen Stroms (Ladungstransport) ermöglicht wird.
Als Verbraucher (Stromverbraucher oder elektrische Verbraucher) werden Bauelemente eines elektrischen Stromkreises bezeichnet, mit Hilfe derer elektrische Energie in andere Energieformen umgewandelt wird.
Grundschaltungen
Zu den Grundlagen der Elektrotechnik zählt die Berechnung von Reihenschaltungen und Parallelschaltungen in Gleichstromkreisen und Wechselstromkreisen. Schaltungen dieser Art werden auch als Grundschaltungen bezeichnet. Nachfolgend wird auf diese eingegangen.
1. Reihenschaltung:
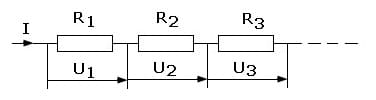
Die Reihenschaltung (Serienschaltung) beschreibt die Hintereinanderschaltung der Bauelemente einer elektrischen Schaltung in der Form, dass diese einen einzelnen Strompfad bilden dessen Verbindung keine Abzweigung enthält. Die Stromstärke ist an allen Stellen der Reihenschaltung gleich groß.
Teilspannungen verhalten sich proportional zu den Widerständen, an denen sie abfallen. Die Gesamtspannung der elektrischen Quelle teilt sich auf alle Bauteile auf. Die Summe aller Teilspannungen entspricht der Gesamtspannung.
2. Parallelschaltung:
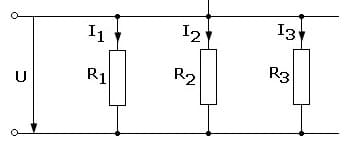
Die Parallelschaltung beschreibt die Anordnung der Bauelemente einer elektrischen Schaltung in der Form, dass diese jeweils über ihre Eingänge und Ausgänge miteinander verbunden sind. Sie ist das Gegenstück zur Reihenschaltung. An all ihren Elementen liegt dieselbe elektrische Spannung an.
Der durch ihre Bauelemente fließende Strom teilt sich in allen Knotenpunkten auf und die Summe aller fließender Teilströme entspricht dem Gesamtstrom.
Mit Hilfe dieses Programmmoduls können Berechnungen mit den Grundschaltungen für Ohmsche Widerstände (Widerstandsberechnungen), Kondensatoren und Spulen durchgeführt werden. Hierbei werden alle in der Schaltung auftretenden Teilströme und Teilspannungen ermittelt und ausgegeben.
I - Reihenschaltung

Abbildung 1 - Reihenschaltung von Widerständen

Abbildung 2 - Reihenschaltung von Kondensatoren

Abbildung 3 - Reihenschaltung von Spulen
1. Reihenschaltung von Widerständen:
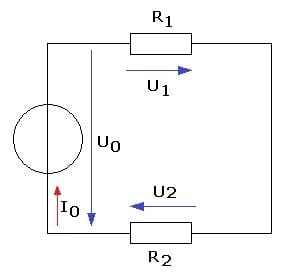
Bei einer Reihenschaltung von n Widerständen (Festwiderständen) ist der Gesamtwiderstand RGes gleich der Summe der Einzelwiderstände.

2. Reihenschaltung von Kapazitäten (Kondensatoren):
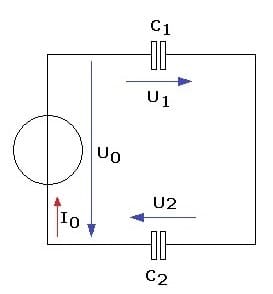
Bei einer Reihenschaltung von n Kapazitäten addieren sich die Kehrwerte der Einzelkapazitäten zum Kehrwert der Gesamtkapazität CGes auf.

3. Reihenschaltung von Induktivitäten (Spulen):
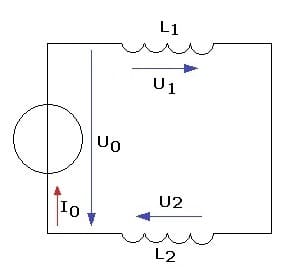
Bei einer Reihenschaltung von n Induktivitäten ist die Gesamtinduktivität LGes gleich der Summe der Einzelinduktivitäten.

4. Gesamtstromstärke und Gesamtspannung bei Reihenschaltungen:
Die Stromstärke (Gesamtstromstärke) IGes, die mehrere in Reihe geschaltete Widerstände, Kapazitäten oder Induktivitäten durchfließt, ist an allen Stellen der Reihenschaltung gleich.

Die an einer Reihenschaltung anliegende Gesamtspannung UGes ist gleich der Summe der n einzelnen Teilspannungen.

RGes,R1,R2,Rn: Widerstand [Ω]
CGes,C1,C2,Cn: Kapazität [F]
LGes,L1,L2,Ln: Induktivität [H]
IGes,I1,I2,In: Strom [A]
UGes,U1,U2,Un: Spannung [V]
II - Parallelschaltung

Abbildung 1 - Parallelschaltung von Widerständen

Abbildung 2 - Parallelschaltung von Kondensatoren

Abbildung 3 - Parallelschaltung von Spulen
1. Parallelschaltung von Widerständen:
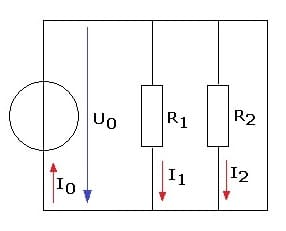
Bei einer Parallelschaltung von n Widerständen addieren sich die Kehrwerte der Einzelwiderstände zum Kehrwert des Gesamtwiderstandes RGes (Ersatzwiderstand) auf.

Bei einer Parallelschaltung wird aus parallel geschalteten Widerständen der Ersatzwiderstand berechnet. Der Ersatzwiderstand Rges ist die aus parallel geschalteten Widerständen errechnete Größe, welche zum Ersatz des gesamten in dieser Parallelschaltung wirkenden elektrischen Widerstands herangezogen wird.
Sind lediglich zwei Widerstände parallelgeschaltet, so kann die vereinfachte Form zur Berechnung des Ersatzwiderstands genutzt werden. Diese lautet:
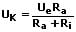
Aufgrund der Tatsache, dass an allen parallelgeschalteten Widerständen die gleiche Spannung liegt, gilt:
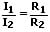
Stromteilerregeln:
Allgemein gelten bei der Parallelschaltung von Widerständen die beiden Stromteilerregeln. Eine Stromteilerregel beschreibt, wie bei einem gegebenem Gesamtstrom in einem Stromkreis, die Teilströme einer Parallelschaltung von Widerständen zu berechnen sind. Diese lauten wie nachfolgend aufgeführt.
Stromteilerregel 1:
Die Ströme, die durch zwei parallel geschaltete Widerstände fließen, verhalten sich zueinander umgekehrt wie die entsprechenden Widerstände. Es gilt:
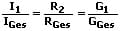
Stromteilerregel 2:
Das Verhältnis zweier Teilströme entspricht dem umgekehrten Verhältnis der jeweiligen Widerstände bzw. dem Verhältnis der jeweiligen Leitwerte. Es gilt:
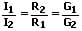
2. Parallelschaltung von Kapazitäten (Kondensatoren):
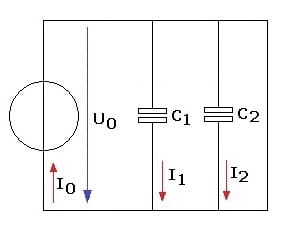
Bei einer Parallelschaltung von n Kapazitäten ist die Gesamtkapazität CGes gleich der Summe der Einzelkapazitäten.

Bei einer Parallelschaltung wird aus parallel geschalteten Kapazitäten die Ersatzkapazität berechnet. Die Ersatzkapazität Cges ist die aus parallel geschalteten Kapazitäten errechnete Größe, welche zum Ersatz der gesamten in dieser Parallelschaltung wirkenden elektrischen Kapazität herangezogen wird.
3. Parallelschaltung von Induktivitäten (Spulen):
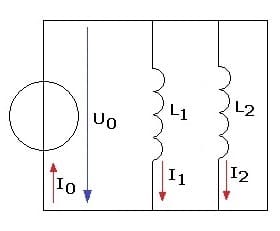
Bei einer Parallelschaltung von n Induktivitäten addieren sich die Kehrwerte der Einzelinduktivitäten zum Kehrwert der Gesamtinduktivität LGes auf.

Bei einer Parallelschaltung wird aus parallel geschalteten Induktivitäten die Ersatzinduktivität berechnet. Die Ersatzinduktivität Iges ist die aus parallel geschalteten Induktivitäten errechnete Größe, welche zum Ersatz der gesamten in dieser Parallelschaltung wirkenden elektrischen Induktivität herangezogen wird.
4. Gesamtstromstärke und Gesamtspannung bei Parallelschaltungen:
Die Gesamtstromstärke Iges teilt sich bei einer Parallelschaltung von n Widerständen, Kapazitäten oder Induktivitäten gemäß der Knotenregel auf n Teilstromstärken auf.

An allen n Widerständen, Kapazitäten oder Induktivitäten einer Parallelschaltung liegt die gleiche Spannung an. Diese ist gleich der Gesamtspannung Uges.

RGes,R1,R2,Rn: Widerstand [Ω]
CGes,C1,C2,Cn: Kapazität [F]
LGes,L1,L2,Ln: Induktivität [H]
IGes,I1,I2,In: Strom [A]
UGes,U1,U2,Un: Spannung [V]
Programmbedienung
Legen Sie durch die Aktivierung des entsprechenden Kontrollschalters fest, ob Sie Analysen mit einer Reihenschaltung oder einer Parallelschaltung durchführen möchten. Wählen Sie hierauf aus, ob die Untersuchungen mit Widerstand, Kapazität oder Induktivität praktiziert werden sollen.
Durch die bei den entsprechenden Bauelementen angeordneten Rollbalken können Sie deren entsprechende Werte festlegen. Mit Hilfe des unten positionierten Rollbalkens kann die der Schaltung zur Verfügung stehende Spannung eingestellt werden.
Bei Gleichstromschaltungen können hierbei Untersuchungen mit Ohmschen Widerständen durchgeführt werden. Bei Wechselspannungen hingegen können Schaltungen mit induktiven und kapazitiven Widerständen analysiert werden. In diesen Fällen lässt sich zudem der Einfluss der Frequenz der Wechselspannung auf den Stromfluss untersuchen.
Nach jeder Änderung werden die an den Bauelementen abfallenden Teilspannungen und fließenden Ströme in Teilstromkreisen ausgegeben.
Innerer Widerstand - Ausgangswiderstand
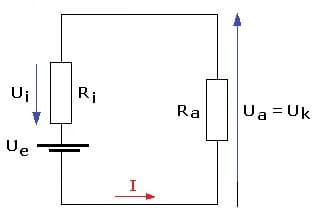
Als innerer Widerstand (oder Innenwiderstand bzw. Ausgangswiderstand bezeichnet) wird der Widerstand einer Spannungsquelle bezeichnet. Dieser sowie die äußeren Widerstände eines Stromkreises bestimmen die Stromstärke dessen. Für den gesamten Stromkreis gilt:
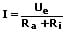
I: Gesamtstrom des Stromkreises [A]
Ue: Urspannung (Quellenspannung) [V]
Ri: Innerer Widerstand [Ω]
Ra: Äußerer Widerstand [Ω]
In einem geschlossenen Stromkreis werden folgende Potenzialdifferenzen unterschieden:
Quellenspannung (Urspannung) Ue:
Die Quellenspannung (Urspannung) ist die Leerlaufspannung die zwischen den Polen der Spannungsquelle bei nicht geschlossenem Stromkreislauf abfällt.
Innerer Spannungsabfall Ui:
Der innere Spannungsabfall ist die Spannung die aufgrund des inneren Widerstand der Spannungsquelle abfällt.
Klemmenspannung Uk:
Als Klemmenspannung wird die Leerlaufspannung die zwischen den Polen der Spannungsquelle bei geschlossenem Stromkreislauf abfällt, bezeichnet.
Für die Klemmenspannung gilt:
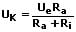
Sie ist die Sunmme aller einzelner äußerer Spannungsabfälle.
UK = U1 + U2 + U3 + ....
Ue: Urspannung [V]
Ri: Innerer Widerstand der Spannungsquelle [Ω]
Ra: Summe aller außerer Widerstände [Ω]
UK: Klemmenspannung [V]
U1,U2,U3 ..: Äußere Spannungsabfälle [V]
Als Leerlaufspannung U0 wird die an einer offenen Spannungsquelle gemessene elektrische Spannung bezeichnet, die zwischen den Klemmen anliegt. Sie ist die Spannung an der Ausgangsseite einer Spannungsquelle, wenn kein Verbraucher an sie angeschlossen ist.
Ausgangsspannung: Als Ausgangsspannung wird die elektrische Spannung bezeichnet, die am Ausgang eines elektrischen Schaltkreises einem Verbraucher zur Verfügung steht.
Unbelastete Spannungsquelle - Belastete Spannungsquelle - Leerlaufspannung - Quellenspannung - Kurzschlussstrom
Unbelastete Spannungsquelle:
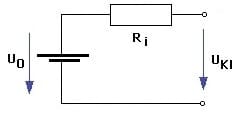
Jede reale Spannungsquelle (elektrische Quelle) besitzt einen Innenwiderstand. Da bei einer unbelasteten Spannungsquelle (Leerlauf) kein geschlossener Stromkreis vorliegt und kein elektrischer Strom fließt, kann an ihm kein Spannungsabfall entstehen. Die an der elektrischen Quelle anliegende Spannung wird in diesem Fall als Leerlaufspannung UL bezeichnet. Die an den Anschlüssen der Quelle abfallende Spannung wird Klemmenspannung UKl genannt. Für den unbelasteten Fall gilt:
I = 0
UKl = U0
Belastete Spannungsquelle:
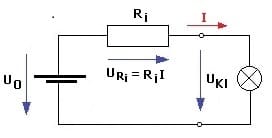
Wird die Spannungsquelle mit einem äußeren Widerstand Ra belastet, so bricht die Klemmenspannung UKl ein. Dies wird von dem durch den Innenwiderstand Ri stattfindenden Stromfluss verursacht, der einen Spannungsabfall am Innenwiderstand der Spannungsquelle bewirkt. Die Ausgangsspannung einer realen Spannungsquelle reduziert sich bei zunehmenden Laststrom. Für die Klemmenspannung gilt in diesem Fall:
UKl = U0 - Ri·I
Kurzschlussstrom:
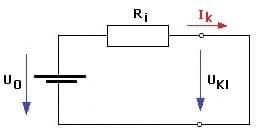
Von einem Kurzschlussstrom (maximalen Strom) wird gesprochen, wenn die Klemmenspannung den Wert Null erreicht hat. In diesem Fall fließt ein durch den Innenwiderstand Ri begrenzter Strom, der Kuzschlussstrom IK. Für ihn gilt:
IK = U0/Ri
U0: Quellenspannung (Leerlaufspannung) [V]
UKl: Klemmenspannung [V]
IK: Kurzschlussstrom [A]
I: Im Stromkreis fließender Strom [A]
Ri: Innenwiderstand der Stromquelle [Ω]
Ideale Spannungsquelle - ideale Stromquelle:
Eine ideale Spannungsquelle verfügt über keinen Innenwiderstand (Ri = 0). Sie hat an ihren Anschlüssen, unabhängig davon ob sie belastet ist oder nicht, stets die selbe Spannung. Die Ausgangsspannung U0 einer idealen Spannungsquelle reduziert sich bei derer Belastung nicht, sondern bleibt konstant. Spannungsquellen dieser Art sind nicht herstellbar und existieren in der Realität nicht, da deren Innenwiderstand Null Ohm betragen müsste.
Auch eine ideale Stromquelle existiert nicht, da deren Innenwiderstand unendlich groß sein müsste und ein solcher nicht vorhanden ist.
Kirchhoffsche Gesetze - Maschensatz - Knotenregel
Die vom deutschen Physiker Gustav Robert Kirchhoff im Jahre 1845 formulierten Kirchhoffschen Gesetze bzw. Kirchhoffsche Regeln beschreiben zwei grundlegende Gesetzmäßigkeiten der Elektrotechnik. Dies sind die Knotenregel (erste Kirchhoffsche Regel) sowie der Maschensatz (die Maschenregel oder Kirchhoffsche Maschenregel).
Diese Regeln dienen zur Berechnung elektrischer Netzwerke und finden Anwendung in der elektrischen Schaltungstechnik. Mit ihrer Hilfe werden elektrische und elektronische Schaltkreise hinsichtlich dort fließender Ströme und an Bauteilen anliegender Spannungen berechnet. Alle sich auf einer Leiterbahn befindenden Punkte können als Knoten in Betracht genommen werden. Als Knoten wird ein Kreuzungspunkt mehrerer Leiter bezeichnet.
1. Kirchhoffsches Gesetz (Knotenregel oder Knotensatz):
Das 1. Kirchhoffsche Gesetz (die Knotenregel) lautet:
In einer Stromverzweigung eines elektrischen Netzwerks ist die Summe der zufließenden Ströme gleich der Summe der abfließenden Ströme.
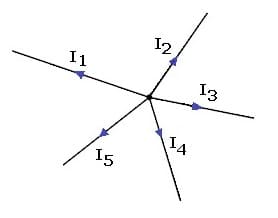
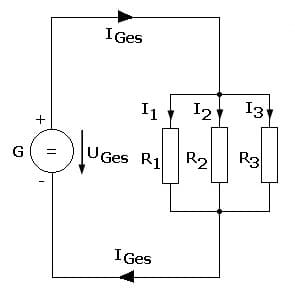
Dies bedeutet: In jeder Stromverzeigung ist die Summe der Zweigströme gleich dem Gesamtstrom. Es gilt:
IGes = I1 + I2 + I3 + ....
2. Kirchhoffsches Gesetz:
Das 2. Kirchhoffsche Gesetz (der Maschensatz) lautet:
In einem geschlossenen Stromkreis ist die Summe aller Teilspannungen gleich der Urspannung der Quelle.
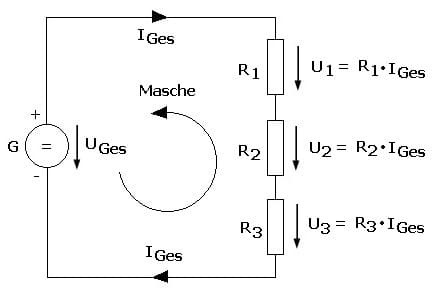
Es gilt:
UGes = U1 + U2 + U3 + ....
Elektrische Arbeit - Elektrische Leistung - Nutzleistung - Verlustleistung - Nutzenergie - Endenergie

Abbildung 1 - Elektrische Arbeit bei konstanter Leistung
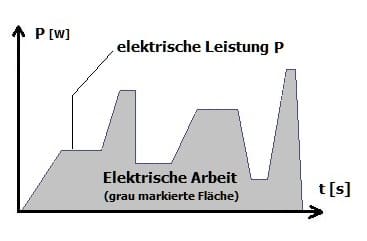
Abbildung 2 - Elektrische Arbeit bei sich verändernder Leistung
Die elektrische Arbeit beschreibt, wieviel elektrische Energie in einem Stromkreis in andere Energiearten transformiert wird. Die elektrische Leistung ist eine Größe, die Auskunft darüber erteilt, welche Menge elektrischer Arbeit vom elektrischen Strom binnen einer Sekunde in elektrische Energie oder andere Energiearten umgewandelt wird.
Unter der Voaraussetzung, dass der elektrische Strom sowie die elektrische Spannung während der verstrichenen Zeit (in einem Gleichstromkreis) konstant gehalten wurden, kann die verrichtete elektrische Arbeit wie folgt berechnet werden:
W = U·I·t = I2Rt = U2t/R
W: Elektrische Arbeit [Ws]
U: Spannung [V]
I: Stromstärke [A]
t: Zeit [s]
Als gängige Einheiten werden für die elektrische Arbeit die folgenden verwendet:
Wattsekunde [Ws]
Wattstunde [Wh]
Kilowattstunde [kWh]
1 Wh = 3600 Ws
1 kWh = 1000 Wh = 3 600 000 Ws
Einheiten der elektrischen Arbeit können wie folgt umgerechnet werden:
Kalorie: 1 cal = 4,19 J
Kilopondmeter: 1 kpm = 9,81 J
Kilowattstunde: 1 kWh = 3,6·106 J = 3,6 MJ
Die elektrische Leistung kann unter den oben gezeigten Bedingungen mit folgender Formel berechnet werden:
P = U·I = I2R = U2/R
P: Elektrische Leistung [W]
U: Spannung [V]
I: Stromstärke [A]
Als Nutzleistung wird die erzeugte, nutzbare Leistung bezeichnet, die vom Verbraucher im Normalbetrieb aufgenommen wird. Sie beschreibt die gewonnene Nutzenergie je Zeiteinheit. Als Nutzenergie wird derjenige Teil der Endenergie bezeichnet, der einem Endverbraucher in nutzbarer Form zur Verfügung steht. Bedingt durch Umwandlungs- und Übertragungsverluste ist die Nutzenergie geringer als die zur Verfügung gestellte Endenergie.
Mit dem Begriff Verlustleistung wird die Differenz zwischen aufgenommener und abgegebener Leistung eines Geräts oder Prozesses angegeben. Als Endenergie wird die von Haushalten, Gewerbe, Industrie sowie Dienstleistungen in einer Volkswirtschaft verwendete Energie bezeichnet.
Stromdichte
Die Stromdichte beschreibt den Stromfluss je Querschnittsfläche (den durch eine Querschnittsfläche tretenden elektrischen Strom). Sie charakterisiert die Belastung eines Leiters anhand des durch ihn fließenden Stroms. Die Erwärmung eines Leiters hängt insbesondere von diesem Sachverhalt ab. Je größer die Stromdichte in einem Leiter ist, desto mehr erwärmt sich dieser. Für die Stromdichte gilt:
J = I/A
J: Stromdichte [A/m²]
I: Strom [A]
A: Querschnittsfläche des Leiters [m²]
Allgemein werden Leiter bautechnisch auf eine Stromdichte von 6 A/mm² ausgelegt. Die maximal zulässige Stromdichte in Kupferleitungen beträgt nach der VDE 100-Norm beispielsweise 16 Ampere bei einem Querschnitt von 1 mm² und 27 Ampere bei 2,5 mm².
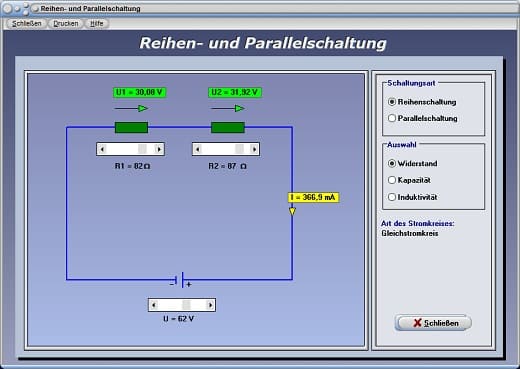
Abb. 1 - Modul Reihenschaltung
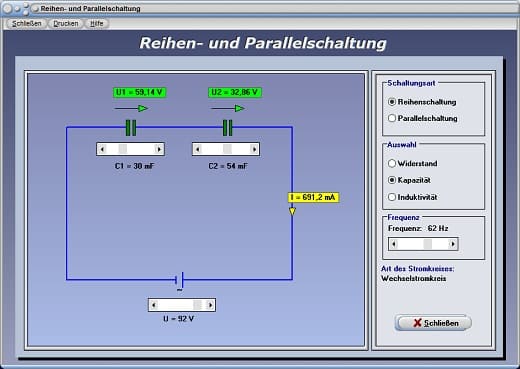
Abb. 2 - Modul Reihenschaltung
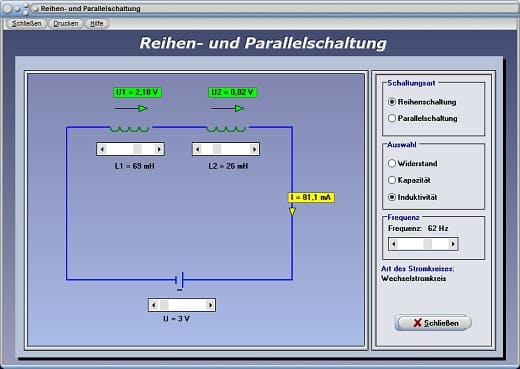
Abb. 3 - Modul Reihenschaltung
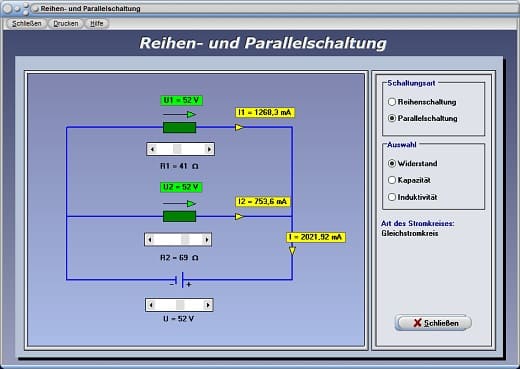
Abb. 4 - Modul Parallelschaltung
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Reihenschaltung zu sowie unter Wikipedia - Parallelschaltung zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
Lissajousche Figuren - Widerstände im Wechselstromkreis - Messbrücke - Widerstandsgesetz - Kondensator Ladung - Entladung - Kondensator - Kapazitäten - Plattenkondensator - Transformator - Schwingungsüberlagerung - RC-Kreis - RL-Kreis - RLC-Kreis - Resonanz - Wechselstromkreis
Unterprogramm Reihen- und Parallelschaltung

PhysProf 1.1 - Unterprogramm RLC-Kreis

MathProf 5.0 - Unterprogramm Kurven in Parameterform

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
















