PhysProf - Reale Gase - Ideale Gase - Gasgesetz - Gaskonstante - Mol

Fachthemen: Reales Gas - Ideales Gas - Gesetze von Gay Lussac - Zustandsgleichung - Gasdichte - Normvolumen - Mol - Molares Volumen - Molare Masse - Joule Thomson Effekt - Kompressionsfaktor - Realgasfaktor
PhysProf - Thermodynamik - Eine Software zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen zur Unterstützung des Unterrichts naturwissenschaftlicher Fächer sowie für alle die sich für Physik interessieren.

Online-Hilfe für das Modul
zur grafischen Darstellung und Auswertung von Druck-Volumen-Diagrammen und zur Ermittlung der kritischen Temperatur realer Gase.
Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden physikalischen Sachverhalte.
Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.

Weitere relevante Seiten zu diesem Programm
Themen und Stichworte zu diesem Modul:Reale Gase - Reales Gas - Thermische Zustandsgleichung - Kritischer Druck - Kritisches Volumen - Kritische Temperatur - Kritischer Punkt - pV-Diagramm - Zustandsdiagramm - Zustandsgleichung - Gas - Gase - Gaskonstante - Universelle Gaskonstante - Allgemeines Gasgesetz - Zustandszahl - Gleichung - Dichte - Druck - Gasdruck - Gasvolumen - Gastemperatur - Gasgleichung - Ideale Gasgleichung - Verhalten - Allgemeine Gaskonstante - Dalton - Dalton Gesetz - Daltonsches Gesetz - Partialdruck - Partialdrücke - Gesamtdruck - Tabelle - Van der Waals Konstanten - Binnendruck - Van-der-Waals - Gleichung - Kovolumen - Kohäsionsdruck - Volumen - Temperatur - Eigenschaften - Einführung - Berechnen - Ideales Gasgesetz - Allgemeine Gasgleichung - Einheit - Physikalische Einheit - Grundlagen - Formel - Formelzeichen - Verändern - Veränderung - Ändern - Änderung - Was - Wie - Weshalb - Was ist - Warum - Bedeutung - Was bedeutet - Erklärung - Einfach erklärt - Herleitung - Beweis - Beschreibung - Grundlagen - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Aufgaben - Abituraufgaben - Lösungen - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Gleichung - Beispiel - Ideale Gase - Ideales Gas - Gasgesetz - Gasgesetze - Gay Lussac - Gay Lussac Gesetz - 1. Gesetz - 2. Gesetz - Gesetz von Amontos - Amontos - Verflüssigung - Gasverflüssigung - Joule Thomson Effekt - Koeffizient - Inversionstemperatur - Gasdichte - Normdichte - Normdruck - Normvolumen - Normliter - Normkubikmeter - Umrechnung - Umrechnen - Universelle Gasgleichung - Spezifische Gaskonstante - Stoffmenge - Molare Masse - Molare Gaskonstante - Mol - Stoffmengen - Stoffe - Teilchen - Begriff - Begriffe - Mittlere freie Weglänge - Freie Weglänge - Molar - Kinetische Gastheorie - Rechnen - Molmenge - Molzahl - Molares Volumen - Spezifisches Volumen - Molares Normvolumen - Molvolumen - Stoffmengenkonzentration - Molarität - Molare Konzentration - Mischungskomponente - Stoffgemisch - Absolutdruck - Überdruck - Eigenschaften - Rechner - Bild - Grafik - Vorgang - Vorgänge - Diagramm - Berechnung - Darstellen - Grafische Darstellung - Realgasfaktor - Kompressionsfaktor |
 |  |
Reales Gas - Ideales Gas
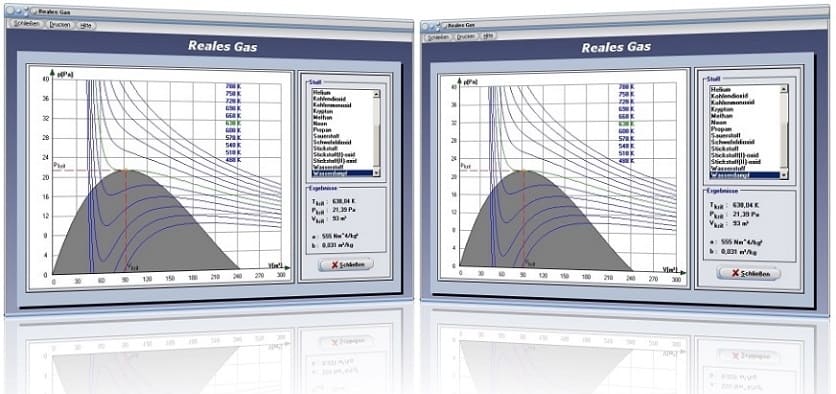
Modul Reales Gas
Das Unterprogramm [Thermodynamik] - [Reales Gas] stellt das Druck-Volumen-Diagramm realer Gase für bestimmte Temperaturen dar.

Reales Gas - Abbildung 1

Reales Gas - Abbildung 2
Verhalten von Gasen: Die meisten Gase zeigen bei atmosphärischem Druck ideales Verhalten. Von diesem jedoch weichen sie bei steigendem Druck oder fallender Temperatur stark ab, da die Dichte eines Gases zunimmt und die Moleküle im Mittel nicht mehr sehr weit voneinander entfernt sind. Die Van-der-Waals-Gleichung ist eine Zustandsgleichung, welche das Verhalten realer Gase über weite Druckbereiche besser beschreibt als die Zustandsgleichung für ideale Gase. Für n Mole eines Gases lautet diese:

Der sogenannte Binnendruck wird durch am²/V² beschrieben. Als Kovolumen wird das kleinste Volumen bezeichnet, auf welches die Moleküle der Gasmasse gebracht werden können.
Das Programm ermittelt in diesem Modul die kritischen Werte für Temperatur, Druck und Volumen des Gases, welche bedeutenden Einfluss auf die Phasenumwandlung gasförmig-flüssig haben und stellt die vorliegenden Sachverhalte in einem Diagramm dar. Es sind dies kritischer Druck, kritische Temperatur und kritisches Volumen. Gase lassen sich oberhalb der kritischen Temperatur nicht mehr ausschließlich durch Kompression verflüssigen, vielmehr bedarf es hierfür einer entsprechenden Temperaturreduzierung.
Kritischer Punkt: Am kritischen Punkt verschwinden die Unterschiede zwischen beiden Aggregatzuständen der flüssigen und gasförmigen Phase eines Stoffs, da die Dichten in beiden Fällen identisch sind.
Beim Zustandsdiagramm handelt es sich im vorliegenden Fall um eine grafische Darstellung verschiedener Zustände realer Gase. Die grün gekennzeichnete Kurve in diesem Diagramm beschreibt hierbei die Isotherme der kritischen Temperatur. Nur unterhalb dieser Temperatur lassen sich Gase unter Druck verflüssigen.
Der markierte Wendepunkt mit waagrechter Tangente entspricht dem Punkt des kritischen Drucks und des kritischen Volumens. Zwischen den kritischen Werten eines Gases und den Van-der-Waals-Konstanten a und b bestehen folgende Beziehungen:



Hierbei sind:
p: Gasdruck [Pa]
V: Gasvolumen [m³]
m: Gasmasse [kg]
R: Gaskonstante [J/(kgK)]
T: Gastemperatur [K]
a: Van-der-Waals-Konstante [N·m4/kmol²]
b: Van-der-Waals-Konstante [m³/kmol]
TKr: Kritischer Wert von Temperatur [K]
VKr: Kritischer Wert von Volumen [m³]
pKr: Kritischer Wert Druck [Pa]
Die Konstante a beschreibt die innere Druckerhöhung durch die zusätzlich vorhandene kinetische Energie im anziehenden Potential (Kohäsion). Die Konstante b beschreibt die Reduktion des freien Volumens durch die endliche Ausdehnung der Moleküle. Diese Konstanten werden aus experimentell bestimmbaren kritischen Daten errechnet. Die beiden Konstanten a (Kohäsionsdruck) und b (Kovolumen) werden auch als Van-der-Waals Konstanten (Van der Waals Konstanten) des betreffenden Gases bezeichnet.
Bei der Darstellung ist der Bereich des Phasenübergangs gasförmig-flüssig grau gefärbt. Nur innerhalb dieses Bereichs kann das Gas durch Komprimierung verflüssigt werden. Links dieses Bereichs existiert das Gas als Flüssigkeit, rechts davon als Gas bzw. als Dampf.
Die Gaskonstante wird auch als universelle Gaskonstante, molare Gaskonstante, oder allgemeine Gaskonstante R bezeichnet. Es handelt sich um eine Konstante aus der Thermodynamik, die bei der Zustandsgleichung idealer Gase auftritt.
Spezifische Gaskonstante: Bei dieser Gaskonstante handelt es sich um eine Kenngröße eines Gases, die von der universellen Gaskonstante R = 8,314472 J/(mol K) abgeleitet wird.
Programmbedienung
Durch die Auswahl eines entsprechenden Eintrags aus der Liste wird das Zustandsdiagramm des gewählten Gases dargestellt und die entsprechenden kritischen Werte und Konstanten werden angezeigt. Unterhalb des Diagramms werden die Werte für Gasvolumen V und Gasdruck p bei aktuell vorhandender Mauscursorposition ausgegeben.
Ideale Gase - Reale Gase - Gasgesetze - Kinetische Gastheorie
Gase setzen sich aus Atomen und Molekülen zusammen. Diese Elementarteilchen bewegen sich im von ihnen beanspruchten Raum geradlinig, regellos und mit hoher Geschwindigkeit. Zwischen ihnen wirken intermolekulare Kräfte.
Ideale Gase:
Ein ideales Gas ist ein idealisiertes Modell des in der Praxis vorkommenden realen Gases, welches in der Physik sowie in Bereichen der Chemie zum Einsatz kommt, um thermodynamische Prozesse von Gasen zu interpretieren und entsprechende Vorgänge physikalisch näherungsweise beschreiben und (vereinfacht) berechnen zu können. Anhand zugrunde liegender Gesetzmäßigkeiten können mit Hilfe dieses Modells, welches unter anderem als kinetische Gastheorie bezeichnet wird, die bei Gasen vorhandenen Beziehungen zwischen den Zustandsgrößen Druck, Volumen und Temperatur dargelegt und interpretiert werden.
Kinetische Gastheorie:
Mittels der kinetischen Gastheorie wird die räumliche Verteilung der Gasteilchen sowie deren Geschwindigkeitsverteilung beschrieben. Die Grundannahmen der kinetischen Gastheorie lauten wie folgt:
- Die Bewegung von Gasteilchen erfolgt ungeordnet und regellos
- Bei Stößen die zwischen einer Gefäßwand und den Gasteilchen zustande kommen handelt es sich um elastische Stöße
- Kräfte zwischen einzelnen Gasteilchen werden lediglich bei bei deren Zusammenstoßen aufeinander ausgeübt
- Die Durchmesser einzelner Gasteilchen sind wesentlich geringer als die Distanzen die diese zueinander besitzen
Reale Gase:
Ein reales Gas ist ein Gas, bei welchem Wechselwirkungskräfte zwischen einzelnen Atomen bzw. Molekülen wirken. Als reale Gase werden die in der Natur vorkommenden Gase bezeichnet.
Gasgesetze:
Mit dem Begriff Gasgesetze werden diejenigen physikalischen Gesetze bezeichnet, die das Verhalten idealer und realer Gase beschreiben und die Relation zwischen deren Zustandsgrößen Druck p, Volumen V, Temperatur T sowie Stoffmenge n bzw. Masse m oder Teilchenzahl N schaffen.
Gesetze von Gay Lussac
Das 1. Gesetz von Gay-Lussac besagt, dass der Quotient aus Volumen V und Temperatur T eines idealen Gases bei konstanter Stoffmenge n konstant ist, solange der Druck p nicht verändert wird. Es gilt V ~ T und p = konstant und somit:
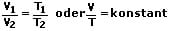
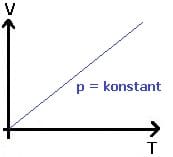
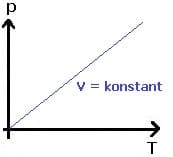
Das 2. Gesetz von Gay-Lussac besagt, dass der Quotient aus Druck p und Temperatur T eines idealen Gases bei konstanter Stoffmenge n konstant ist, solange das Volumen V nicht verändert wird. Dieses Gesetz wird auch als Gesetz von Amontos bezeichnet. Es gilt p ~ T und V = konstant und somit:
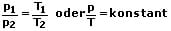
Zustandsgleichung des idealen Gases - Allgemeines Gasgesetz - Ideales Gasgesetz - Ideale Gasgleichung - Thermische Zustandsgleichung
Die erste Form der Zustandsgleichung des idealen Gases besagt, dass beim Vorliegen einer bestimmten Masse (Menge) eines idealen Gases das Produkt aus Druck p und Volumen V, geteilt durch die den absoluten Temperaturwert T konstant ist. Diese erste Form der Zustandsgleichung des idealen Gases lautet:
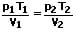
oder
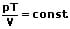
p1: absoluter Druck des Gases zu Beginn, bei Zustand 1 [Pa]
p2: absoluter Druck des Gases bei Zustand 2 [Pa]
T1: Temperatur des Gases zu Beginn, bei Zustand 1 [K]
T2: Temperatur des Gases bei Zustand 2 [K]
V1: Volumen des Gases zu Beginn, bei Zustand 1 [m³]
V2: Volumen des Gases bei Zustand 2 [m³]
Die obig gezeigten Zustandsgleichungen haben lediglich beim idealen Gas Gültigkeit, bei realen Gasen können sie als Näherung verwendet werden.
Allgemeines Gasgesetz (ideales Gasgesetz bzw. ideale Gasgleichung):
Mit dem allgemeinen Gasgesetz wird ein Modell beschrieben, bei dem zugrundegelegt wird, dass die Atome eines idealen Gases kein Volumen besitzen und in keinerlei Wechselwirkung zueinander stehen. Dieses Gesetz wird auch als allgemeine Gasgleichung, ideale Gasgleichung oder ideales Gasgesetz bzw. thermische Zustandsgleichung bezeichnet. Die hierfür relevante eigentliche Form (zweite Form) der Zustandsgleichung idealer Gase lautet wie folgt:
p·V = m·R·T
Sie existiert zudem in verschiedenen extensiven Formen, welche nachfolgend gezeigt werden:
p·V = n·Rm·T
p·V = m/M·Rm·T
p·V = N·kB·T
Die zuletzt aufgeführte Form dieser Gleichung wird auch mit dem Begriff universelle Gasgleichung bezeichnet.
p: absoluter Druck des Gases [Pa]
V: Volumen des Gases [m³]
m: Masse des Gases [kg]
R: spezifische Gaskonstante [J/(kg·K)]
n: Stoffmenge des Gases [mol]
T: Temperatur des Gases [K]
M: molare Masse [kg/mol]
Rm: molare Gaskonstante [J/(mol·K)]
N: Teilchenzahl
kB: Boltzmann-Konstante = 1,3806491·10-23 J/K
Hinweis:
Der Absolutdruck bezeichnet den Druck in Relation zum Druck Null im Vakuum. Als Überdruck wird der relativ zum Atmosphärendruck bzw. Luftdruck gemessene Druck angegeben.
Dichte eines Gases - Gasdichte - Zustandszahl - Normliter - Normkubikmeter - Normvolumen
Die Dichte eines Gases (Gasdichte) hängt vom Zustand dessen ab. Sie ändert sich abhängig von seinem Druck sowie seiner Temperatur. Angaben hierzu beziehen sich stets auf den vorhandenen Druck sowie seine Temperatur.
Allgemein gilt:
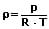
Als Normdichte wird die Dichte eines Stoffes oder eines Elements unter folgenden Bedingungen definiert: Temperatur: 273,15 K ; Druck: 101 325 Pa. Für die Normdichte eines Gases bei einem Druck von 101 325 Pa (Normdruck) sowie einer Temperatur von 273,15K (0°C) gilt:
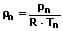
p: Gasdruck [Pa]
ρ: Dichte des Gases bei einem Druck und einer Temperatur [kg/m³]
T: Temperatur des Gases [K]
R: spezifische Gaskonstante [J/(kg·K)]
Die Umrechnung der Dichte eines Gases abhängig von seinem Zustand kann folgendermaßen durchgeführt werden:
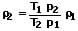
p1: Gasdruck bei Zustand 1 [Pa]
p2: Gasdruck bei Zustand 2 [Pa]
T1: Temperatur des Gases bei Zustand 1 [K]
T2: Temperatur des Gases bei Zustand 2 [K]
ρ1: Dichte des Gases bei Zustand 1 [kg/m³]
ρ2: Dichte des Gases bei Zustand 2 [kg/m³]
Ein Vergleich zwischen den Volumina zweier Gase kann lediglich dann erfolgen, wenn sich diese Angaben auf denselben Druck sowie dieselbe Temperatur dessen beziehen. Auch hierbei werden ein Druck von 101325 Pa (Normdruck) sowie eine Temperatur von 273,15K (0°C) vorausgesetzt. Es gilt:
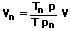
p: Druck des Gases [Pa]
T: Temperatur des Gases [K]
V: Volumen des Gases [m³]
pn: Normdruck des Gases [Pa]
Tn: Normtemperatur des Gases [K]
Vn: Normvolumen des Gases [m³]
Die Zustandszahl Z beschreibt das Verhältnis eines Gasvolumens, welches sich Normzustand befindet zum entsprechenden Gasvolumen im Betriebszustand. Es gilt:
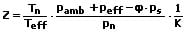
Z: Zustandszahl
Vb: Volumen des Gases im Betriebszustand [m³]
TN: Normtemperatur = 273,15 K
Teff: Abrechnungstemperatur [K]
pn: Normluftdruck = 1,01325 bar
pamb: Jahresmittelwert des Luftdrucks [Pa]
peff: Effektivdruck des Gases [Pa]
ρ·ps: Wasserdampfpartialdruck des Gases [Pa]
mit:
ρ: relative Luftfeuchtigkeit
ps: Sättigungsdruck
K: Kompressibilitätszahl
Als Abrechnungsgröße bei Erdgas wird das Volumen des Gases Vn benutzt, welches dieses im Normzustand besitzt. Die Umrechnung des Betriebsvolumens Vb auf das Normvolumen Vn des Gases erfolgt wie nachfolgend aufgeführt:
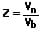
Z: Zustandszahl
Vb: Volumen des Gases im Betriebszustand [m³]
Vn: Volumen des Gases im Normzustand [m³]
Bei einem Normliter handelt es sich um die Gasmenge, die im physikalischen Normzustand (bei 1013 mbar sowie 0°C) exakt ein Volumen von 1 Liter ausfüllt. Er beschreibt kein Raummaß, sondern eine Gasmenge, die anhand räumlicher Abmessungen widergespiegelt wird.
Bei einem Normkubikmeter handelt es sich um die Menge eines Gases, die in einem Volumen eines Kubikmeters dessen enthalten ist.
Als Normvolumen wird das Gasvolumen bezeichnet, welches im physikalischen Normzustand vorliegt. Bei sämtlichen idealen Gasen nimmt ein Mol Gas bei einem von Druck 1,013 bar und einer Temperatur von 0 °C ein Volumen von 22,4141 Litern ein, wenn der Druck 1,013 bar und die Temperatur 0 °C beträgt. Dieses Volumen wird molares Normvolumen genannt.
Dalton Gesetz - Partialdruck
Als Partialdruck wird der Teildruck einer einzelnen Komponente eines Gasgemischs bezeichnet. Der Gesamtdruck bildet sich aus den Partialdrücken einzelner Komponenten des Gases. Das Gesetz von Dalton (Dalton Gesetz) besagt, dass sich der Gesamtdruck in einem Gasgemisch, welches sich aus nicht reagierenden Gasen zusammensetzt, dem insgesamt ausgeübten Gesamtdruck der Summe der Partialdrücke aller einzelnen Gase entspricht. Es gilt:

pi: Partialdrücke [Pa]
ptotal: Gesamtdruck[Pa]
Mol - Molares Volumen - Molare Masse - Molare Gaskonstante - Stoffmenge - Spezifisches Volumen - Stoffmengenkonzentration
Die Stoffmenge (auch Molmenge oder Molzahl) kennzeichnet die Anzahl gleichartiger Teilchen die in einem System (einer Stoffportion) vorkommen. Sie trägt das Formelzeichen n und ist eine Basisgröße des internationalen Einheitensystems SI.
Ein Mol beschreibt die Stoffmenge, die soviele Teilchen enthält, wie Atome in 12 g des Kohlenstoffisotops C12. Ein Mol beinhaltet definitionsgemäß bei allen Stoffen exakt 6,02214076·1023 Teilchen. Unter dem Begriff Teilchen sind unter anderem Atome, Moleküle, Ionen, Elektronen sowie andere Partikel zu verstehen.
Molare Masse:
Als molare Masse wird der Quotient der Masse und der Stoffmenge eines Stoffs bezeichnet. Es gilt:
M = m/n
M: Molare Masse [kg/mol]
m: Masse [kg]
n: Stoffmenge [mol]
Spezifisches Volumen:
Mit dem spezifischen Volumen wird das Verhältnis von Volumen V zur Masse m beschrieben. Es gilt:
v = V/m = 1/ρ
v: spezifisches Volumen [m³/kg]
V: Volumen [m³]
m: Masse [kg]
ρ: Dichte [kg/m³]
Molvolumen (molares Volumen):
Mit Hilfe des molaren Volumens (Molvolumen) Vm wird angegeben, welches Volumen ein Mol einer Substanz einnimmt. Es beschreibt das Volumen, welches von 6,022·1023 Teilchen einer Substanz eingenommen wird.
Vm = V/n = M/ρ
Vm: Molvolumen [m³/mol]
V: Volumen [m³]
ρ: Dichte [kg/m³]
n: Stoffmenge [mol]
M: Molare Masse [kg/mol]
Stoffmengenkonzentration:
Mit der Stoffmengenkonzentration (Molarität oder molare Konzentration) ci wird der Quotient aus der Stoffmenge ni einer Mischungskomponente i und dem Gesamtvolumen V des Stoffgemischs bezeichnet. Es gilt:
ci = ni/V
ci: Stoffmengenkonzentration [mol/m³]
ni: Stoffmenge [mol]
V: Volumen des Stoffgemischs [m³]
Mittlere freie Weglänge:
Die mittlere freie Weglänge beschreibt die Strecke (die räumliche Distanz), die von einem Molekül nach zwei Stößen mit anderen Molekülen im Mittel zurückgelegt wird. Die kann mit Hilfe einer der nachfolgend gezeigten Formeln bestimmt werden:
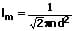
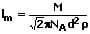
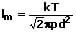
l: Mittlere freie Weglänge [m]
n: Molekülzahldichte
d: Durchmesser eines Moleküls [m]
p: Druck des Gases [Pa]
T: Temperatur des Gases [K]
ρ: Dichte des Gases [kg/m³]
M : Molare Masse [kg/mol]
NA: Avogadro-Konstante = 6,022·1023 1/mol
k: Boltzmann-Konstante = 1,381·10-23 J/K
Joule Thomson Effekt - Verflüssigung von Gasen - Gasverflüssigung
Die Ursache des Joule-Thomson-Effekts beruht auf der Wechselwirkung von Gasteilchen. Teilchen dieser Art ziehen sich bei einer Vergrößerung ihres gegenseitigen Abstands bedingt durch die Van-der-Waals-Kräfte an. Hierbei muss Arbeit verrichtet werden und das Gas kühlt ab. Besitzen die Teilchen hingegen einen geringen Abstand, so stoßen diese sich wieder ab und erfahren eine Beschleunigung. Das Verhältnis dieser beiden Effekte hängt von der Temperatur sowie dem Druck des Gases ab.
Allgemein gilt: Die Kompression eines Gases führt zu einem Temperaturanstieg dessen, während die Entspannung ein Absinken der Gastemperatur bewirkt.
Reale Gase gewinnen innere Energie auch durch Kompression. Diese Tatsache wird als Joule-Thomson-Effekt bezeichnet. Hierdurch lassen sich mittels der Expansion eines Gases sehr niedrige Temperaturen erzeugen. Ein Gasstrom wird wiederholt einer Drosselstelle zugeführt, wo das entsprechende Gas eine adiabatische Expansion erfährt.
Die Abkühlung dessen bei dieser Expansion erfolgt nach dem Joule-Thomson-Effekt. Anwendung findet dieser bei der Gasverflüssigung. Hierzu zählt unter anderem die Verflüssigung von Luft nach dem Karl von Linde-Verfahren. Der Joule-Thomson-Koeffizient μ beschreibt die Stärke sowie die Art der Temperaturänderung des Gases. Eine Abkühlung tritt lediglich ein, wenn die Anfangstemperatur des Gases geringer ist als die Inversionstemperatur dessen (μ < 0). Für den Joule-Thomson-Koeffizienten gilt:
μ = ΔT/Δp
μ: Joule-Thomson-Koeffizient [K/Pa]
ΔT: Temperaturänderung bei Entspannung [K]
Δp: Druckänderung bei Entspannung [Pa]
Die Inversionstemperatur Ti bei der Entspannung eines Gases kann bestimmt werden mit:
Ti = 2a/(Rb)
Ti: Inversionstemperatur [K]
a: Van-der-Waals-Konstante [Nm4/kg²]
b: Van-der-Waals-Konstante [m³/kg]
R: Gaskonstante [J/(Kg·K)]
In der folgenden Tabelle ist die Inversionstemperatur einiger Gase aufgeführt.
| Gas | Inversionstemperatur Ti [K] |
| Argon | 1018 |
| Helium | 35 |
| Kohlendioxid | 2053 |
| Kohlenmonoxid | 908 |
| Luft | 893 |
| Sauerstoff | 1043 |
| Stickstoff | 856 |
| Wasserstoff | 222 |
Kompressionsfaktor - Realgasfaktor
Für ideale Gase besitzt die Zustandsgleichung p·Vm = Rm·T Gültigkeit. Bei realen Gasen sind diesbezüglich jedoch Abweichungen feststellbar. Der sogenannte Realgasfaktor oder Kompressionsfaktor Z beschreibt diesen Zusammenhang und es gilt in diesem Fall:
p·Vm = Z·Rm·T
Der Realgasfaktor berechnet sich mit Z = Vmz / Vm
Er beschreibt das Verhältnis des molaren Volumens des realen Gases zum molaren Volumen des idealen Gases an (bei gleicher Temperatur und gleichem Druck).
Z: Realgasfaktor oder Kompressionsfaktor []
Vmz: Molares Volumen des Gases bei realem Zustand [m3/kmol]
Vm: Molares Volumen des Gases bei idealem Zustand [m3/kmol]
Tabelle - Spezifische Gaskonstante
Nachfolgend aufgeführt sind die Werte für die spezifische Gaskonstante einiger Gase.
| Gas | Gaskonstante R [J/[kg·K]] |
| Ammoniak | 481 |
| Argon | 208 |
| Chlor | 115 |
| Ethan | 273 |
| Helium | 2078 |
| Kohendioxid | 188 |
| Kohlemonoxid | 297 |
| Krypton | 99 |
| Luft | 287 |
| Methan | 518 |
| Neon | 412 |
| Propan | 185 |
| Sauerstoff | 260 |
| Schwefeldioxid | 127 |
| Stickstoff | 297 |
| Wasserstoff | 4127 |
Tabelle - Druck - Volumen - Gase - Temperatur
In diesem Modul besteht die Möglichkeit, sich Druck-Volumen-Temperatur-Diagramme für nachfolgend aufgeführte Gase ausgeben zu lassen.
| Gase |
| Ammoniak |
| Argon |
| Butan |
| Chlor |
| Chlorwasserstoff |
| Ethan |
| Ethen |
| Ethin |
| Ethylchlorid |
| Helium |
| Kohlendioxid |
| Kohlenmonoxid |
| Krypton |
| Methan |
| Neon |
| Propan |
| Sauerstoff |
| Schwefeldioxid |
| Stickstoff |
| Stickstoff(I)-oxid |
| Stickstoff(II)-oxid |
| Wasserstoff |
| Wasserdampf |
In der folgenden Tabelle sind die Werte der Van-der-Waals Konstanten a und b einiger Gase aufgeführt.
| Gas | a [103·n·m4/kmol2] | b [m3/kmol] |
| Ammoniak | 424 | 0,0372 |
| Argon | 136 | 0,0322 |
| Butan | 1490 | 0,125 |
| Chlor | 655 | 0,056 |
| Chlorwasserstoff | 361 | 0,0397 |
| Ethan | 551 | 0,0641 |
| Ethen | 452 | 0,0571 |
| Ethin | 441 | 0,0508 |
| Helium | 3,34 | 0,024 |
| Kohlendioxid | 362 | 0,0425 |
| Kohlenmonoxid | 147 | 0,0395 |
| Krypton | 231 | 0,0394 |
| Methan | 229 | 0,0427 |
| Neon | 21 | 0,0169 |
| Propan | 93 | 0,09 |
| Sauerstoff | 137 | 0,0316 |
| Schwefeldioxid | 680 | 0,0564 |
| Stickstoff | 136 | 0,0385 |
| Wasserdampf | 555 | 0,031 |
| Wasserstoff | 25 | 0,026 |
| Xenon | 413 | 0,0512 |
Die nachfolgend dargestellte Tabelle zeigt die kritische Temperatur tKrit und den kritischen Druck pKrit einiger Gase.
| Gas | tKrit [K] | pKrit [MPa] |
| Ammoniak | 132 | 11,3 |
| Argon | -122 | 4,9 |
| Butan | 152 | 3,8 |
| Chlor | 152 | 7,7 |
| Chlorwasserstoff | 144 | 8,31 |
| Ethan | -32 | 4,88 |
| Ethen | 9,3 | 5,07 |
| Ethin | 35,9 | 6,26 |
| Flour | -129 | 5,6 |
| Helium | 3,34 | 0,23 |
| Hexan | -268 | 3,03 |
| Kohlendioxid | 31 | 7,38 |
| Kohlenmonoxid | -140 | 3,5 |
| Krypton | -63,8 | 5,49 |
| Methan | -82 | 4,64 |
| Neon | -229 | 2,65 |
| Propan | 97 | 4,23 |
| Sauerstoff | -118 | 5,08 |
| Schwefeldioxid | 158 | 7,88 |
| Stickstoff | -147 | 3,39 |
| Wasserdampf | 374 | 22 |
| Wasserstoff | -140 | 1,3 |
Normdichte einiger Gase (gasförmiger Stoffe)
In der folgenden Tabelle (Dichtetabelle) ist die Dichte (Normdichte) einiger gasförmiger Stoffe (Gase) aufgeführt (bei 0°C und 101,3 Pa):
| Gas | Dichte in kg/m³ |
| Ammoniak | 0,7714 |
| Argon | 1,786 |
| Butan | 2,709 |
| Chlor | 3,214 |
| Chlorwasserstoff | 1,489 |
| Helium | 0,1785 |
| Kohlendioxid | 1,9769 |
| Kohlenmonoxid | 1,25 |
| Krypton | 3,744 |
| Luft | 1,2929 |
| Methan | 0,7168 |
| Neon | 0,9002 |
| Propan | 2,0096 |
| Sauerstoff | 1,42895 |
| Stickstoff | 1,2505 |
| Wasserstoff | 0,08988 |
| Xenon | 5,897 |
Weitere Screenshots zu diesem Modul

Reales Gas - Abbildung 3

Reales Gas - Abbildung 4

Reales Gas - Abbildung 5

Reales Gas - Abbildung 6
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Reales Gas sowie unter Wikipedia - Van der Waals-Gleichung und unter Wikipedia - Thermische Zustandsgleichung idealer Gase zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
Isochore Zustandsänderung - Isobare Zustandsänderung - Isotherme Zustandsänderung - Adiabatische Zustandsänderung - Carnotscher Kreisprozess - Aggregatzustände - Mischungsregel - Molekülgeschwindigkeit
Unterprogramm Reales Gas

PhysProf 1.1 - Unterprogramm RLC-Kreis

MathProf 5.0 - Unterprogramm Kurven in Parameterform

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















