PhysProf - Elektrische Ladung - Feldstärke - Feldlinien
Fachthemen: Plattenkondensator - Elektrisches Feld - Ladung - Feldlinien - Elektrische Feldstärke
PhysProf - Elektrotechnik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Ausbildung, die Schule und den Beruf.
Online-Hilfe für das Modul
zur Untersuchung des Einflusses verschiedener Größen auf die Stärke elektrischer Felder beim Plattenkondensator.
Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden physikalischen Sachverhalte und eignet sich zudem als Begleitung zu Versuchen im Physikunterricht.
Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.
Weitere relevante Seiten zu diesem Programm
Themen und Stichworte zu diesem Modul: |
 |  |
Plattenkondensator - Elektrisches Feld
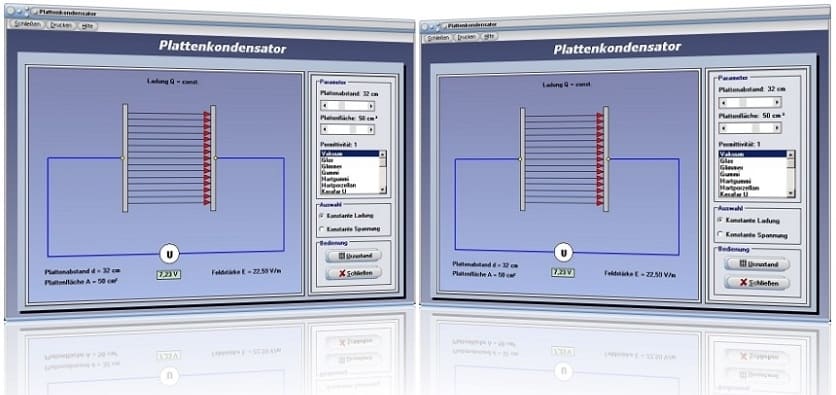
Modul Plattenkondensator
Mit Hilfe des Unterprogramms [Elektrotechnik] - [Plattenkondensator] kann die Abhängigkeit der Stärke eines elektrischen Feldes von ihren Einflussgrößen untersucht werden.
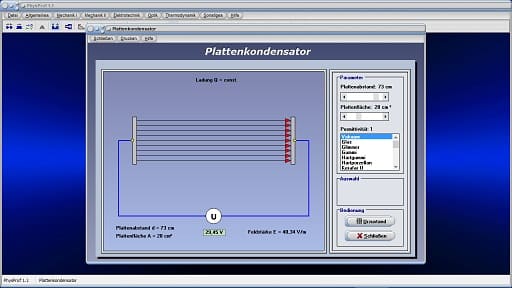
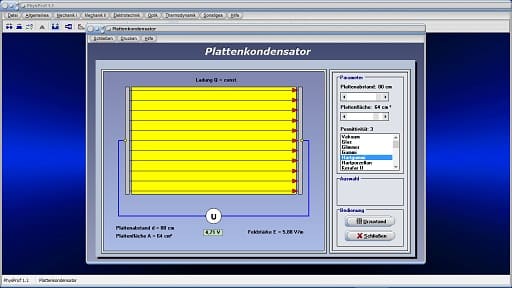
I - Konstante Ladung
Plattenkondensator - Konstante Ladung - Abbildung 1
Plattenkondensator - Konstante Ladung - Abbildung 2
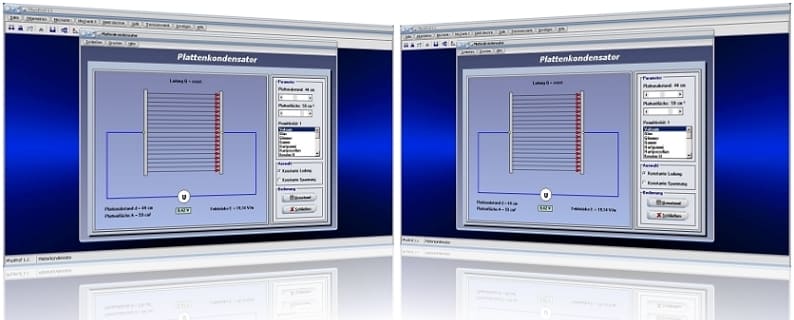
II - Konstante Spannung
Plattenkondensator - Konstante Spannung - Abbildung 1
Plattenkondensator - Konstante Spannung - Abbildung 2
Ein Plattenkondensator besteht aus zwei parallelen, ebenen Metallplatten, welche sich in geringem Abstand zueinander befinden und durch ein isolierendes Medium (Dielektrikum) voneinander getrennt sind. Er wird zur Speicherung elektrischer Ladungen verwendet. Werden die Platten elektrisch aufgeladen, so besitzt eine Platte eine positive, die andere eine negative Ladung und zwischen beiden Platten baut sich elektrische Spannung auf.
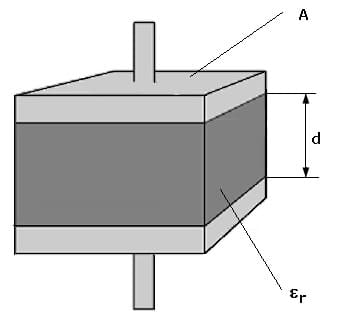
Die Potentialdifferenz U sowie die Feldstärke E hängen von der Zusammensetzung der Platten, deren Abstand und dem sich zwischen ihnen befindlichen Dielektrikum sowie der Fläche A der Platten ab.
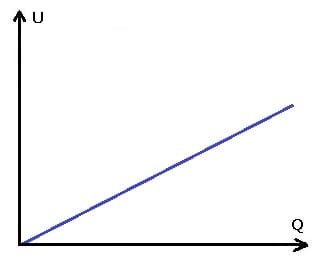
Als Kapazität C eines Körpers wird das Verhältnis der zugeführten Ladung Q und der hierbei entstandenen Spannung U bezeichnet. Die SI-Einheit der Kapazität ist das Farad (F). Es gilt:
C: Kapazität [F]
Q: Zugeführte Oberflächenladung [C]U: Spannnung [V]
Die Kapazität eines Kondensators gibt die gespeicherte Ladung bezogen auf die Potentialdifferenz an. Daraus folgt für die Kapazität eines Plattenkondensators, falls das elektrische Feld E durch ein Dielektrikum abgeschirmt wird.
C: Kapazität des Kondensators [F]
A: Fläche der Platten des Kondensators [A]
d: Plattenabstand [m]
e0: Absolute Dielektrizitätskonstante e0 = 8,85419·10-12 As/Vm
εR: Permittivitätszahl
Das elektrische Feld E (E Feld) wird durch die Potentialdifferenz U zwischen den Platten bestimmt. Hierbei gilt:
E: Elektrische Feldstärke [V/m]
U: Spannung zwischen zwei Platten [V]
d: Plattenabstand [m]
Hieraus resultiert für die Potentialdifferenz zwischen den Platten. Für sie gilt:
U: Spannung (Potentialdifferenz) zwischen zwei Platten [V]
Q: Oberflächenladung (elektrische Ladung bzw. Elektrizitätsmenge) [C]
C: Kapazität [F]
Programmbedienung
Mit Hilfe dieses Moduls können Sie die zuvor aufgeführten Abhängigkeiten untersuchen. Hierbei wird die Stärke des elektrischen Feldes durch die Anzahl eingezeichneter Pfeile symbolisiert. Es stehen zwei verschiedene Methoden zur Auswahl, um sich die Zusammenhänge begreiflich machen zu können. Bei einer wird die elektrische Ladung, bei der anderen wird die Spannung konstant gehalten. Bei letzterer wird der Kondensator an eine Spannungsquelle angeschlossen. Auswählen können Sie die gewünschte Untersuchung, wenn Sie den entsprechenden Kontrollschalter Konstante Ladung bzw. Konstante Spannung aktivieren.
Mit den dafür vorgesehenen Rollbalken Plattenabstand und Plattenfläche können Sie den Abstand der Kondensatorplatten sowie die Plattenfläche des Kondensators festlegen.
Aus der zur Verfügung stehenden Listbox können Sie ein Dielektrikum auswählen. Je höher dessen Permittivitätszahl ist, desto größer wird die Kapazität des Kondensators. Bei konstanter Ladung werden hierbei sowohl die elektrische Spannung als auch das zwischen den Platten existierende elektrische Feld kleiner.
In den Anfangszustand zurückversetzen lassen können Sie durchgeführte Einstellungen wieder, wenn Sie die Schaltfläche Urzustand bedienen.
Elektrisches Feld - Ladung - Feldlinien - Elektrische Feldstärke
Elektrisches Feld (E Feld):
Als elektrisches Feld (E-Feld) wird ein physikalisches, räumliches Feld bezeichnet, bei dem die Kräfte (insbesondere Feldkraft bzw. die Coulombkraft) elektrisch geladener Teilchen wirken. Dessen Stärke (Intensität) und räumliche Verteilung (Ausrichtung) wird über die elektrische Feldstärke beschrieben. Verursacht werden elektrische Felder von elektrischen Ladungen sowie durch Veränderungen magnetischer Felder.
Elektrische Ladung:
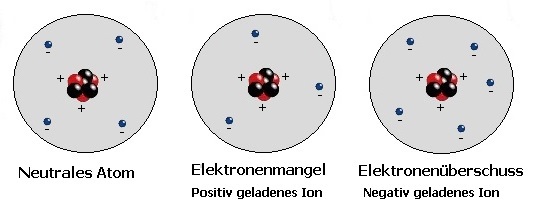
Geladene Teilchen: Körper können elektrisch neutral sowie positiv oder negativ geladen sein. Die Oberfläche vieler nichtleitender Materialien kann durch Reibung elektrisch geladen werden. Hierbei werden dieser entweder Elektronen entzogen oder zugeführt. Besteht ein Elektronenmangel, so ist der Körper positiv geladen. Bei einem Elektronenüberschuss ist der Körper hingegen negativ geladen. Gleichartig geladene Körper stoßen sich ab, ungleichartig geladene Körper ziehen sich an. Die elektrische Ladung eines Körpers beschreibt die Dimension dessen Elektronenüberschusses bzw. Elektronenmangels. Die SI-Einheit der elektrischen Ladung ist das Coulomb (C). Ein elektrisches Feld überträgt die Kraftwirkung der vorhandenen elektrischen Ladung auf andere Ladungen.
1. Elektrische Ladung und elektrischer Strom
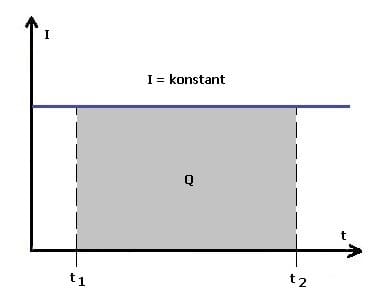
Abb 1: Elektrische Ladung - Konstante Stromstärke
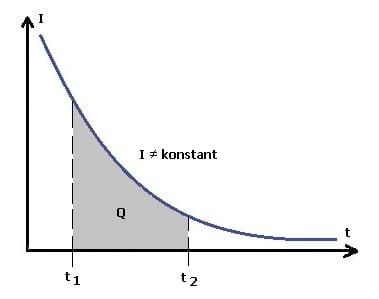
Abb 1: Elektrische Ladung - Nicht konstante Stromstärke
Elektrische Ladung ist das Produkt aus Stromstärke und Zeit.
Als Stromfluss werden im Allgemeinen die innerhalb eines elektrischen Leiters fließenden Elektronen verstanden.
Bei konstantem Stromfluss gilt:
Q = I·t
bzw.
Q = I·Δt
Bei nicht konstantem Stromfluss gilt:
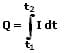
Q: Elektrische Ladung die binnen eines Zeitraums Δt durch den Leiter fließt [C]
I: Stromstärke [A]
Δt,t : Zeit [s]
2. Ladungserhaltungssatz:
Innerhalb eines abgeschlossenen Systems (Raums) bleibt die Gesamtladung erhalten. Hierbei gilt für alle positiven wie negativen Ladungen der Ladungserhaltungssatz:
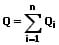
QGes: Gesamtladung [C]
Qi: Teilladungen [C]
3. Elementarladung:
Als Elementarladung wird die Ladung eines einzelnen Elektrons bezeichnet. Sie ist die kleinste aller existierenden Ladungsmengen. Die gesamte Ladung freier Teilchen beträgt stets ein Vielfaches dieser kleinsten Ladung. Für sie gilt:
Q = N·e
Die elektrische Elementarladung besitzt den Wert e = 1,60217733·10-19 Coulomb.
Die Ladung 1 Coulomb entspricht der Ladung von ca. 6,24·1018 Elektronen.
Q: Gesamtladung [C]
N: Anzahl einzelner Ladungen
e: Elementarladung [C]
4. Elektronenfluss:
Mit dem Elektronenfluss wird die binnen eines bestimmten Zeitraums durch einen Leiter mit konstantem Querschnitt geflossene Ladung beschrieben. Die Anzahl der Elektronen die hierbei durch den entsprechenden Leiter fließen, kann wie folgt berechnet werden:
N = I·Δt/e
N: Anzahl der Elektronen
I: Stromstärke [A]
e: Elementarladung [C]
Δt: Zeitraum [s]
5. Amperestunde - Amperesekunde:
Eine Amperestunde ist eine Maßeinheit für die elektrische Ladung. Als Amperestunde wird diejenige Ladungsmenge bezeichnet, die innerhalb einer Stunde durch einen Leiter fließt, wenn der hierbei fließende elektrische Strom konstant 1A beträgt.
Eine Amperesekunde ist diejenige Ladungsmenge, die innerhalb einer Sekunde durch einen Leiter fließt, wenn der hierbei fließende elektrische Strom konstant 1A beträgt.
Angaben dieser Art finden bei Batterien und Akkumulatoren Anwendung um deren zur Verfügung stehende elektrische Ladung kennzuzeichnen.
1 Amperestunde [Ah] = 3 600 Amperesekunden [As]
Feldlinien - Feldlinienmodell:
Feldlinienmodell: Elektrische Felder werden duch Feldlinien dargestellt. Grafiken dieser Art werden als Feldlinienbilder bezeichnet. Linien dieser Art ermöglichen die Betrachtung der auf einen Körper von einem Feld ausgehenden Kräfte. Die an eine Feldlinie gelegte Tangente zeigt die Wirkungsrichtung der Kraft im jeweiligen Berührungspunkt. Die Dichte dargestellter Feldlinen erteilt Auskunft über die Stärke des wirkenden Feldes.
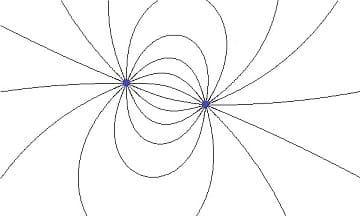
Abb. 1: Elektrische Feldlinien - Beispiel 1
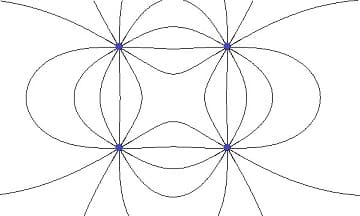
Abb. 2: Elektrische Feldlinien - Beispiel 2
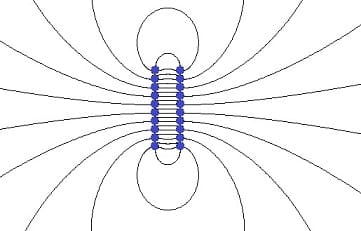
Abb.3: Elektrische Feldlinien - Beispiel 3
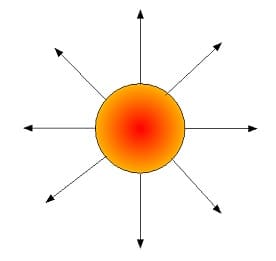
Abb.4: Elektrische Feldlinien - Beispiel 4 (Radialfeld)
Feldlinien (elektrische Feldlinien) verlaufen von positiven Ladungen ausgehend in Richtung der negativen Ladungen. Ihre Austrittsrichtung aus der Oberfläche des entsprechenden Körpers ist stets senkrecht. Abhängig vom Verlauf dieser Feldlinien wird von einem homogenen (parallel verlaufenden), einem inhomogenen oder einem radialen Feldlinienverlauf (radialsymmetrisches Feld) gesprochen. Sie kreuzen sich nicht.
Bei einem Radialfeld nimmt dessen Feldstärke mit zunehmendem Abstand von seinem Austrittszentrum ab. Ein homogenes Feld wird von parallel verlaufenden Feldlinien gebildet, nichtparallel verlaufende Linien bilden ein inhomogenes Feld. Die Feldliniendichte gibt die Dichte eines elektrischen Feldes bei einem bestimmten Ort an und beschreibt damit den Betrag der dort vorliegenden Feldstärke.
Elektrische Feldstärke:
Die Stärke eines elektrischen Feldes wird durch die elektrische Feldstärke ausgedrückt. Dies ist die Kraft, auf die eine Punktladung in diesem Punkt wirkt. Sie ist das Verhältnis der in einem Feld wirkenden Kraft zur Größe dieser Ladung. Es gilt:
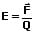
E: Elektrische Feldstärke [V/m]
F: Die im Feld auf eine Ladung wirkende Kraft [N]
Q: Ladung des Feldes [C]
Diese Gleichung gilt prinzipiell für homogene Felder.
Homogenes elektrisches Feld: Von einem homogenen elektrischen Feld wird gesprochen, wenn seine Feldlinen parallel verlaufen und dieselbe Richtung besitzen. Sind diese Eigenschaften nicht vorhanden, so handelt es sich um ein inhomogenes Feld. Bei inhomogenen Feldern besitzt sie Aussagekraft über die (ungleichmäßig verteilte) Stärke des gesamten Feldes.
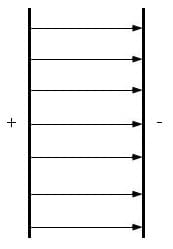
Abb 1: Homogenes elektrisches Feld
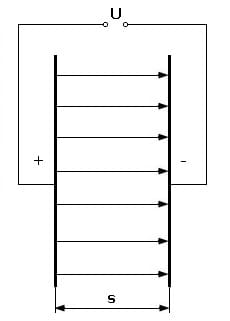
Abb 2: Stärke eines Feldes
Für die Stärke eines Feldes, welches sich zwischen zwei parallel angeordneten Platten befindet, gilt:
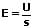
E: Elektrische Feldstärke [V/m]
U: Elektrische Spannung zwischen beiden Platten [V]
s: Abstand der beiden Platten [m]
Die Feldstärke an einer Kugeloberfläche kann wie folgt berechnet werden:
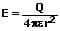
E: Elektrische Feldstärke [V/m]
Q: Ladung an der Oberfläche der Kugel [C]
ε: Permittivität = ε0·εR [F/m]
r: Radius der Kugel [m]
Coulombsches Gesetz - Elektrisches Feld - Elektrische Kraft - Coulombsche Kraft - Coulomb Potential
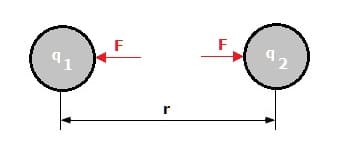
Die elektrische Kraft ist eine auf geladene Körper wirkende Kraft. Zwischen Körpern mit gleicher Ladung wirkt die abstoßend. Auf Körper mit unterschiedlichen Ladungen wirkt sie anziehend. Mit zunehmender Entfernung nimmt die elektrische Ladung nach dem Coulombschen Gesetz ab.
Das Coulombsche Gesetz beschreibt diese zwischen zwei Punktladungen wirkende Kraft. Der Betrag dieser Kraft verhält sich proportional zum Produkt der beiden Ladungsmengen sowie umgekehrt proportional zum Quadrat des Abstands der beiden Kugelmittelpunkte. Dieses Gesetz besitzt auch bei kugelförmig verteilten Ladungen Gültigkeit. Für die Coulombsche Kraft (elektrostatische Anziehungskraft oder elektrostatische Kraft) in einem homogenen Medium gilt allgemein:
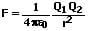
mit
ε = ε0εR
Im Vakuum gilt:
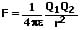
F: Wirkende Kraft zwischen zwei punktförmigen Ladungen [N]
Q1: Ladung in Punkt 1 [C]
Q2: Ladung in Punkt 2 [C]
r: Abstand der beiden Punktladungen [m]
ε: Permittivität = ε0·εR [F/m]
ε0: Elektrische Feldkonstante = 8,854·10-12 F/m
εR: Permittivitätszahl
Für die zwischen zwei Platten wirkende Kraft (beim Plattenkondensator) gilt:
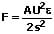
Zudem gilt für die zwischen zwei Platten wirkende Kraft:
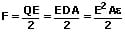
F: Wirkende Kraft zwischen zwei Platten [N]
A: Fläche einer Platte [m²]
U: Spannung zwischen zwei Platten [V]
s: Abstand zweier Platten [m]
E: Elektrische Feldstärke [V/m]
Q: Elektrische Ladung [C]
D: Verschiebungsdichte [C/m²]
ε: Permittivität = ε0·εR [F/m]
Die Verschiebungsdichte beschreibt die Dichte elektrischer Feldlinien bezogen auf eine Fläche.
Hinweis: Eine Tabelle für die Permittivität (Permittivitätszahl, Dielektrizitätszahl) εr einiger Stoffe ist auf der Seite Kondensator - Kapazität zu finden.
Coulomb Potential (elektrostatisches Potential):
Das Coulomb-Potential ist das elektrostatische Potential einer ruhenden Punktladung Q in einem Punkt. Es ist proportional zur potentiellen Energie die zwischen zwei Ladungen q1 und q2 die sich im Abstand r voneinander befinden. Ist diese Ladung in einem Punkt konzentriert, so gilt für eine Punktladung Q mit dem Abstand r:
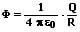
Q: ruhende Punktladung [C]
ε0: Dielektrizitätskonstante des Vakuums (elektrische Feldkonstante) = 8,854·10-12 F/m
r: Abstand der Ladungen [m]
Ist die Ladung nicht in einem Punkt konzentriert, sondern in Form einer Ladungsdichte verteilt, so gilt:
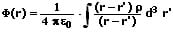
Elektrischer Dipol - Dipolmoment - Dipol - Magnetischer Dipol - Elektrisches Dipolmoment - Magnetisches Dipolmoment
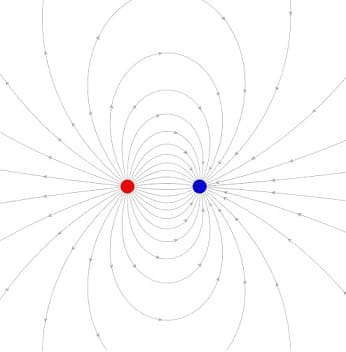
Als Dipol wird eine Anordnung zweier gleich großer, ungleichnamiger Punktladungen (Pole) bezeichnet, die sich in einem Abstand d zueinander befinden. Es kann sich hierbei um magnetische Pole oder elektrische Ladungen handeln. Ein elektrischer Dipol verursacht ein elektrisches Feld in seiner Umgebung und kann elektromagnetische Wellen abgeben.
Das elektrische Dipolmoment ist ein Maß für die Stärke eines Dipolmoleküls und somit für die Polarität eines Moleküls. Das magnetische Dipolmoment beschreibt die auf eine bestimmte Art und Weise die gesamte Feldmenge, die durch einen magnetischen Dipol bedingt wird.
Als elektrisches Dipolmoment p wird das Produkt bezeichnet, welches sich wie folgt ergibt:
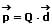
±Q: Ladungen des Dipols [C]
d: Abstandsvektor [m]
p: Elektrisches Dipolmoment [Cm]
Die elektrische Feldstärke in der Umgebung eines elektrischen Dipols kann wie folgt beschrieben werden:
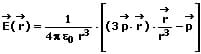
E: Elektrische Feldstärke
e0: Elektrische Feldkonstante
r: Ortsvektor des Ladungspunkts
p·r: Skalarprodukt der beiden Vektoren p und r
Feldenergie - Energiedichte
Feldenergie:
Die in einem elektrischen Feld gespeicherte Energie wird als elektrische Feldenergie bezeichnet. Sie ist die zur Zusammenführung oder Trennung der Ladungen aufzubringende Arbeit. Für einen Kondensator gilt allgemein:
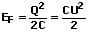
Bei einem aus zwei Platten bestehenden Kondensator gilt für die Feldenergie:
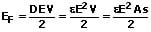
Energiedichte:
Die Energiedichte eines elektrischen Feldes bezeichnet die Verteilung von Energie auf eine Größe. Für sie gilt:
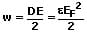
w: Energiedichte [J/m²]
EF: Feldenergie (Energie eines geladenen Kondensators) [J]
E: Elektrische Feldstärke [V/m]
C: Kapazität des Kondensators [F]
D: Verschiebungsdichte [C/m²]
Q: Elektrische Ladung [C]
U: Spannung zwischen zwei Platten [V]
s: Abstand zweier Platten [m]
ε: Permittivität = ε0·εR [F/m]
Elektrostatik - Elektrisches Potential - Potentialdifferenz - Elektrische Energie - Äquipotentialflächen - Äquipotentiallinien - Elektrodynamik - Statische Elektrizität - Statische Aufladung - Elektrostatische Aufladung - Elektrostatisches Feld
Die Elektrostatik befasst sich mit ruhenden elektrischen Ladungen, elektrischen Feldern geladener Körper sowie mit Ladungsverteilungen. Die Erscheinungen der Elektrostatik beruhen auf den Kräften die von elektrischen Ladungen aufeinander ausgeübt werden.
Als Elektrodynamik wird das Teilgebiet der Physik bezeichnet, das sich mit bewegten elektrischen Ladungen beschäftigt. Die Elektrodynamik behandelt insbesondere sich zeitlich verändernde elektrische Felder sowie Magnetfelder.
Statische Elektrizität oder statische Aufladung bzw. elektrostatische Aufladung:
Bei statischer Elektrizität (statischer Aufladung) handelt es sich um eine Erscheinung, die infolge mechanischer Vorgänge wie Reiben, Zersplittern oder Zerreißen oder beim Strömen von Flüssigkeiten oder Gasen auftritt. Hierunter wird eine Anhäufung elektrischer Ladungen verstanden, die durch unterschiedliche Stoffe auf voneinander getrennt positionierten Teilen oder auf leitfähigen Gegenständen infolge von Influenz auftreten. Bei einer Aufladung dieser Art handelt sich somit um eine Häufung elektrischer Ladungen an Gegenständen, die oftrmals durch Reibung verursacht wird. Die statische Elektrizität wird auch statische Aufladung oder elektrostatische Aufladung genannt. Körper oder Gegenstände, die ein Potential dieser Art besitzen werden als statisch aufgeladen, elektrostatisch aufgeladen oder statisch geladen bezeichnet.
Elektrostatisches Feld:
Ein elektrostatisches Feld besteht aus ruhenden Ladungen und innerhalb dessen fließt kein elektrischer Strom.
Elektrostatische Felder und Kräfte entstehen, wenn elektrische Ladungen räumlich voneinander getrennt werden. Das kann durch Reibung zwischen zwei isolierenden Materialien (Reibungselektrizität) geschehen. Ein Beispiel für das Entstehen eines elektrostatischen Feldes ist das Reiben einer Hose auf dem Schonbezug eines Autositzes. Der Körper des Fahrers oder Beifahrers wird hierbei elektrostatisch aufgeladen. Wird von ihm beim Verlassen des Fahrzeugs des Metall des Fahrzeugs berührt, so entsteht durch die Entladung des Körpers ein leichter elektrischer Schock.
Elektrisches Potential:
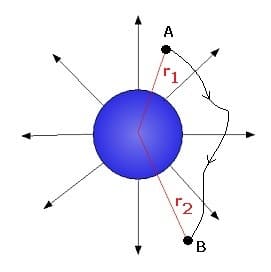
Als elektrisches Potential wird eine physikalische Größe bezeichnet, die die Fähigkeit des inhomogenen elektrischen Feldes beschreibt, Arbeit an einer elektrischen Ladung verrichten. Wird eine Ladung Q in einem derartigen Feld verschoben, so wird Arbeit geleistet, da die Coulombkraft wirksam ist. Durch diese Ladungsverschiebung erhält diese Ladung potentielle Energie.
Je größer die zu verschiebende Ladung ist, desto größer ist die wirkende Coulombkraft und somit auch die hierbei zu verrichtende Arbeit. Das elektrische Potential eines Punktes ist der Quotient aus der potentiellen Energie in diesem Punkt sowie der Ladung des elektrischen Feldes. Für eine Bewegung von Punkt Q zu Punkt A gilt für die zu verrichtende Arbeit:
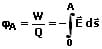
φA: Elektrisches Potential an Stelle A [V]
E: Elektrische Feldstärke [V/m]
s: Weg [m]
W: Arbeit [J]
Als Kontourlinien des elektrischen Potentials werden Linien oder Flächen gleichen Potenzials bezeichnet. Man nennt sie Äquipotenziallinien oder Äquipotenzialflächen. Die potentielle Energie einer Ladung ist auf einer Äquipotentiallinie (Äquipotenzialfläche) stets konstant und sie bewegt sich ohne Kraft- bzw. Arbeitsaufwand.
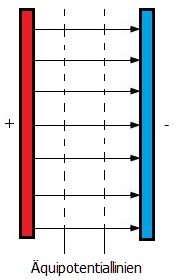
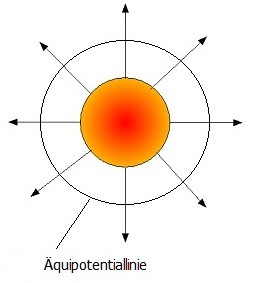
Die Potentialdifferenz (der Potentialunterschied) zwischen zwei beliebigen Punkten eines elektrischen Feldes entspricht der Spannung, die zwischen diesen beiden Punkten anliegt. Zwischen einem Punkt A auf der positiv geladenen Platte und einem Punkt B auf der negativ geladenen Platte eines Kondensators ergibt sich eine Potentialdifferenz und es gilt:
Die Potentialdifferenz zwischen zwei beliebigen Punkten eines elektrischen Feldes entspricht der Spannung, die zwischen diesen beiden Punkten anliegt. Die Ladungsmenge gibt an wie viel elektrische Energie durch die Potentialdifferenz zweier Punkte gebunden ist.
φA: Elektrisches Potential an Stelle A der Probeladung [V]
φB: Elektrisches Potential an Stelle B der Probeladung [V]
Δ Epot: Änderung der potentiellen Energie [J]
q: Ladungsmenge (Probeladung) [V]
U: Potentialdifferenz zwischen den Platten [V]
Für die elektrische potentielle Energie im Abstand d von der Platte B gilt:
Epot = q·φ = q·E·d
Epot: Elektrische potentielle Energie [J]
q: Ladungsmenge [V]
φ: Elektrisches Potential an Stelle der Probeladung [V]
d: Abstand der Energie von Platte [m]
Die elektrische Energie in einem Plattenkondensator beträgt:
EEl = 1/2·C·U²
EEl: Elektrische Energie [J]
C: Kapazität [F]
U: Spannung [V]
Elektrische Flussdichte - Verschiebungsdichte - Flächenladungsdichte
Die dielektrische Verschiebung oder elektrische Flussdichte (auch Verschiebungsdichte, Verschiebungsflussdichte) beschreibt die Dichte der elektrischen Feldlinien in Bezug auf eine Fläche. Sie ist eine vektorielle Größe und das Produkt elektrischen Feldstärke E und der elektrischen Feldstärke ε0. Es gilt:
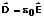
D: Verschiebungsdichte [C/m²]
E: Elektrische Feldstärke [V/m]
ε0: Elektrische Feldkonstante = 8,854·10-12 F/m
Die elektrische Ladungsdichte beschreibt die Ladungsverteilung durch folgende Größen:
- Raumladungsdichte: Ladung pro Volumen
- Oberflächenladungsdichte: Ladung pro Fläche
- Linienladungsdichte: Ladung pro Länge
Die Ladungsverteilung kann in homogener sowie in inhomogener Form vorliegen und kann positive als auch negative Werte besitzen.
Als Flächenladungsdichte (Ladungsdichte je Fläche oder Oberflächenladungsdichte) wird das Verhältnis der auf einer geladenen Fläche im elektrischen Feld existenten Ladung und der geladenen Fläche bezeichnet. Für sie gilt:
σ = Q/A
σ: Flächenladungsdichte [C/m²]
Q: Elektrische Ladung des Leiters an seiner Oberfläche [C]
A: Fläche des Leiters [m²]
Befindet sich das elektrische Feld im Vakuum oder in der Luft, so gilt:
σ = ε0E
σ: Flächenladungsdichte [C/m²]
E: Elektrische Feldstärke [V/m]
ε0: Elektrische Feldkonstante = 8,854·10-12 F/m
Als Ladungsträgerdichte (Ladungsträgerkonzentration) wird die Anzahl der innerhalb eines Körpervolumens vorhandenen Ladungsträger bezeichnet. Sie ist eine ortsabhängige Teilchendichte, die sehr temperaturabhängig ist und wird zur Beschreibung der elektrischen Leitfähigkeit eines Stoffes eingesetzt.
Dielektrische Relaxation: Die dielektrische Relaxation wird der zeitverzögerte Aufbau als Ergebnis der Bewegung der Dipole und Ladungsträger eines dielektrischen Mediums bezeichnet, der durch ein äußerlich angelegtes elektrisches Feld hervorgerufen wird.
Dielektrischer Verlustfaktor - Dielektrischer Verlust: Der dielektrische Verlustfaktor tan δ wird als Maß dafür eingesetzt, zu bestimmen welche Energiemenge ein isoilerender Stoff im Wechselfeld aufnimmt und in Verlustwärme umwandelt. Stoffe mit einem hohen Verlustfaktor eignen sich nicht zum Einsatz als Isolierstoffe bei Hochfrequenzanwendungen.
Elektrische Polarisation: Als elektrische Polarisation (dielektrische Polarisation) wird eine physikalische Größe bezeichnet, die die Stärke des elektrischen Dipolmoments in einem dielektrischen Material charakterisiert und somit beschreibt mit welcher Internsität ein Dielektrikum polarisiert ist.
Elektrische Influenz - Elektrostatische Induktion - Elektronenüberschuss - Elektronenmangel - Statische Elektrizität - Bewegte Ladung
Es existieren zwei unterschiedliche Arten von Ladungen. Dies sind die positive Ladung und die negative Ladung.
Gewöhnlich besitzen Atome in ihrem Kern dieselbe Anzahl positiver Ladungsträger (Protonen) wie auch negative Ladungsträger (Elektronen) die sich in der Hülle dessen befinden. Atome sind somit von außen betrachtet elektrisch neutral.
Liegt bei einem Atom einen Elektronenüberschuss vor, so besitzt es mehr negative als positive Ladungsträger und ist somit nach außen negativ geladen. Herrscht ein Elektronenmangel in der Hülle des Atoms, so ist das Atom nach außen positiv geladen. Atome mit diesen Eigenschaften werden als Ionen bezeichnet. Bezogen auf einen Körper (der aus Atomen besteht) gelten die gleichen Gesetzmäßigkeiten. Somit kann ein Körper als Ganzes sowohl über ein positives, wie auch ein negatives Ladungspotential verfügen (positiv oder negativ geladen sein).
Da geladene Körper Kräfte aufeinander auswirken, stoßen sich gleichartig geladene Körper ab, ungleichartig geladene Körper hingegen ziehen sich gegenseitig an.
Als Influenz (elektrische Influenz, elektrostatische Induktion) wird die räumliche Verschiebung elektrischer Ladungen bezeichnet, welche durch den Einfluss eines elektrischen Feldes verursacht wird. Bei elektrischen Leitern werden frei bewegliche Elektronen an deren Oberfläche transportiert und verändern hierbei ihre Position. Hierdurch bilden sich im entsprechenden Material Zonen unterschiedlicher Ladungsdichte. Die gesamte Ladungsdichte des Leiters bleibt jedoch erhalten.
Ein neutrales Medium besitzt an jeder Position eine einheitliche Anzahl positiver wie auch negativer Ladungsträger. Atomkerne besitzen positive Ladungen, die Elektronen der Atomhülle hingegen negative. Unmittelbar dann, wenn ein elektrisch geladener Körper im Umfeld eines neutralen Leiters positioniert wird, erfolgt eine hierdurch verursachte Trennung der Ladung (Ladungsträger) im Leiter. Die Art der Verteilung dieser internen Ladung wird davon beeinflusst, welche Art der Ladung das äußere Medium besitzt. Sie kann positiv oder negativ sein. Bedingt wird dieser Sachverhalt durch die Gesetzmäßigkeiten des Coulombschen Gesetzes.
Als statische Elektrizität wird eine bewegungslose elektrische Ladung bezeichnet. Hierbei handelt es sich um eine Erscheinung, die an der Oberfläche zweier oder mehrerer unterschiedlicher Stoffe entsteht, wenn diese sich berühren und hierauf mechanisch voneinander getrennt werden. Es erfolgt eine Übertragung negativ geladener Elektronen zwischen den Atomen der entsprechenden Materialien.
Durch bewegte Ladungen werden durch elektromagnetische Magnetfelder gebildet, die hierdurch einen elektrischen Strom erzeugen. Derartige Ladungen üben Kräfte aufeinander aus, deren Ursache nicht dem Coulombschen Gesetz zugrunde liegt. Sie werden durch bewegte Ladungsträger wie Elektronen erzeugt und erfahren in einem Magnetfeld eine ablenkende Kraft, die als Lorentzkraft bezeichnet wird. Diese bewegen sich quer zu den Feldlinien eines elektrischen Feldes und besitzen einen parabelförmigen Verlauf.
Elektroskop - Elektrometer - Aufbau - Funktion - Beschreibung
Das Elektroskop (Elektrometer) ist ein Gerät, welches sich zum Nachweisen und Messen elektrischer Ladungen und Spannungen von Körpern eignet. Die Funktionsweise dessen basiert auf dem Prinzip der kontaktlosen Anziehung und Abstoßung elektrischer Ladungen (Influenz). In der nachfolgenden Beschreibung wird auf den Aufbau und die Funktion des Elektroskops eingegangen.
Das Elektroskop besteht im Wesentlichen aus einem beweglichen elektrisch leitenden Metallstab sowie einem starren Metallzeiger, der drehbar gelagert und mit dem Metallstab vebunden ist. Der Zeiger ist an seinem Drehpunkt mit dem Gehäuse leitend verbunden. Ein derartiges Instrument besitzt keine elektrische Ladung und ist somit elektrisch neutral.
Wird ein geladener Körper in die Nähe des Metalltellers des Elektroskops gehalten, so verschieben sich die Ladungen in ihm.
Zwei unterschiedliche elektrische Ladungen ziehen sich gegenseitig an. Zwei Ladungsträger mit gleichnamiger Ladung stoßen sich ab. Erfolgt dies ohne eine Berührung (ohne elektrischen Kontakt) der Ladungsträger, so wird ein derartiger Vorgang als Influenz bezeichnet.
Wenn ein geladener Stab an ein Elektroskop gehalten wird, dann schlägt der Metallzeiger aus. Wird dieser wieder entfernt, so bleibt der Zeigerausschlag erhalten.
Dieser Stab kann positiv oder negativ geladen sein. Wird er mit dem Elektroskop verbunden, so kommt es zum Ladungsausgleich zwischen dem Stab und dem ladungsfreien Elektroskop.
Ist der Stab positv geladen, so besteht ein Elektronenmangel. Die Elektronen des Elektroskops bewegen sich auf den Stab zu. Das Elektroskop ist somit positiv geladen. Da Metallzeiger und Gehäuse leitend miteinander verbunden sind, ist auch der Zeiger positiv geladen und Metallzeiger und Gehäuse stoßen sich somit gegenseitig ab.
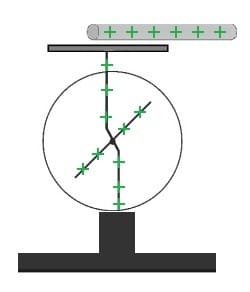
Ist der Stab negativ geladen, so besteht auf ihm ein Elektronenüberschuss. Elektronen des Stabs bewegen sich auf das Gehäuse zu. Hierdurch ist das Elektroskop negativ geladen. Da Metallzeiger und Gehäuse eine leitende Verbindung besitzen, ist auch der Zeiger negativ geladen. Metallzeiger und Gehäuse stoßen sich somit gegenseitig ab.
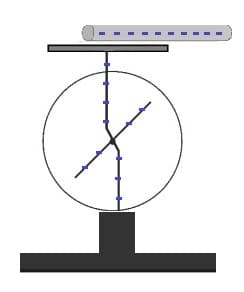
Die Dimension des Zeigerausschlags hängt von der Ladungsmenge ab, die sich auf dem Elektroskop befindet. Je größer die Ladung ist, desto größer ist der Ausschlag des Zeigers.
Mit Hilfe eines Elektroskops kann elektrische Ladung sowie ihre Stärke nachgewiesen werden, jedoch besteht keine Möglichkeit festzustellen, ob diese positiv oder negativ ist.
Ein Elektroskop, welches eine kalibrierte Skala besitzt, wird als Elektrometer bezeichnet.
Ladungstrennung - Reibungselektrizität - Elektronenaffinität
Als Ladungstrennung werden Vorgänge bezeichnet, bei denen die Trennung positiver und negativer Ladungen erfolgt und die absolute Ladung einen von Null verschiedenen Wert aufweist. Dies kann unter anderem durch elektrochemische Vorgänge, durch Influenz oder durch Reibung erfolgen. Hierbei erfolgt die Übertragung der Elektronen eines Körpers auf einen anderen.
Reibungselektrizität: Als Reibungselektrizität wird die beim gegenseitigen Reiben zweier Isolatoren erscheinende entgegengesetzte elektrische Aufladung bezeichnet (Ladungstrennung). Werden zwei Materialien unterschiedlicher Elektronenaffinität miteinander in Kontakt gebracht, so wandern die Elektronen von einem zum anderen Isolator über. Die Reibungselektrizität ist auf den Übergang von Elektronen zwischen zwei sich berührenden Stoffen infolge der Verschiedenheit derer Austrittsarbeit zurückzuführen.
Elektronenaffinität: Als Elektronenaffinität wird die Energie bezeichnet, die freigesetzt wird, wenn ein Atom ein weiteres Elektron aufnimmt.
Ladungserhaltung
Das Gesetz der Ladungserhaltung besagt, dass die Summe aller elektrischen Ladungen in einem isolierten System konstant ist und sich somit niemals ändert. Es besagt auch, dass sich die Erhaltungsgrößen des Systems niemals ändern. Werden in diesem geladene Teilchen erzeugt oder vernichtet, so geschieht dies immer in gleichen Mengen und mit entgegengesetztem Vorzeichen.
Dielektrikum - Nichtleiter - Elektrische Leiter
Nichtleiter (Isolatoren, Dielektrika):
Ein Dielektrikum ist ein elektrisch isolierendes Material, innerhalb dessen sich Ladungsträger nicht frei bewegen können. Es kann sich hierbei um einen Feststoff, eine Flüssigkeit oder ein Gas handeln. Als Isolatoren kommen beim Bau eines Kondensators Nichtleiter zum Einsatz. Als Nichtleiter werden Stoffe bezeichnet, deren elektrische Leitfähigkeit weniger als 10-8 S/cm beträgt. Hierzu zählen insbesondere Kunststoffe, Glas, Glimmer, Gummi, Porzellan, Kerafar, Keramik, Papier, Quarz, Schiefer, Tantaloxid undTeflon. Als Spannungsfestigkeit eines isolierenden Materials wird der Maximalwert eines elektrischen Feldes bezeichnet, dem das isolierende Medium standhalten kann.
Elektrische Leiter (metallische Leiter):
Elektrische Leiter sind Medien, die eine gute elektrische Leitfähigkeit und einen geringen elektrischen Widerstand besitzen und sich somit zum Transport geladener Teilchen (dem Strom) eignen. Hierzu zählen insbesondere Metalle wie Kupfer, Gold, Silber, Platin, Eisen usw.
Durchschlagsfestigkeit - Durchschlagspannung
Bei einer bestimmten Spannung (Durchschlagspannung) bzw. nach Ablauf einer bestimmten Zeit nach dem Anlegen einer hohen Spannung verliert ein Isoliermaterial seine isolierenden Eigenschaften unwiderruflich. Es entsteht eine irreversible Schädigung des Isolierstoffes.
Die Durchschlagfestigkeit (oder Durchschlagsfeldstärke) ist diejenige elektrische Feldstärke derer ein Isolierstoff höchstens ausgesetzt sein darf, ohne dass es zu einem Spannungsdurchschlag kommt.
Die Ermittlung der Durchschlagkraft eines Isolationswerkstoffs erfolgt, indem ein Isolierstoff zwischen zwei Elektroden geklemmt wird, an denen eine elektrische Spannung angelegt wird. Diese wird solange kontinuierlich erhöht bis die Durchschlagfestigkeit überschritten wird und es zu einer strukturellen Schädigung des Werkstoffs kommt.
Die elektrische Durchschlagsfestigkeit ist wie folgt definiert:
Ed = Ud / d
Ed: elektrische Durchschlagfestigkeit [V]
Ud: Durchschlagspannung [V]
d: Dicke der Isolation [m]
Die Angabe der Durchschlagsfestigkeit erfolgt häufig in der Form [kV/mm].
Durchschlagsfestigkeit - Tabelle
Nachfolgend aufgeführt sind die Werte für die Durchschlagsfestigkeit einiger Isolierstoffe.
| Material | Dicke d [mm] | Durchschlagsfestigkeit [kV/mm] |
| Aluminiumoxid | 1 | 17 |
| Diamant | 1 | 2000 |
| Glimmer | 1 | ≤ 60 |
| Hochvakuum | 1 | 20 ... 40 |
| PVC | 1 | 30 |
| PTFE | 1 | 18 ... 100 |
| Polystyrol | 1 | 20 ... 60 |
| Polypropylen | 1 | 52 |
| Plexiglas | 1 | 30 |
| PET | 1 | 20 ... 25 |
| Wasser (destilliert) | 1 | 65 ... 70 |
| Quarzglas | 1 | 25 ... 40 |
| Emaille | 1 | 20 ... 30 |
| Glas | 1 | > 8 |
| Porzellan | 1 | 20 |
| Helium | 1 | 0,15 |
| Luft (trocken) | 1 | 3 |
Plattenkondensator - Konstante Ladung - Abbildung 3
Plattenkondensator - Konstante Ladung - Abbildung 4
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Elektrische Kapazität, unter Wikipedia - Permittivität sowie unter Wikipedia - Kondensator zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
Lissajousche Figuren - Reihen- und Parallelschaltung - Widerstände im Wechselstromkreis - Messbrücke - Widerstandsgesetz - Kondensator Ladung - Entladung - Kondensator - Kapazitäten - Transformator - Schwingungsüberlagerung - RC-Kreis - RL-Kreis - RLC-Kreis - Resonanz - Wechselstromkreis
Unterprogramm Plattenkondensator
PhysProf 1.1 - Unterprogramm RLC-Kreis
MathProf 5.0 - Unterprogramm Kurven in Parameterform
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Physik interaktiv
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
Eine Übersicht aller in MathProf 5.0 zur Verfügung stehender Programmteile finden Sie im MathProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
