PhysProf - Moleküle - Oberflächenspannung - Oberflächenenergie
Fachthemen: Moleküle - Zwischenmolekulare Kräfte - Adhäsion - Kohäsion - Oberflächenspannung - Oberflächenenergie
PhysProf - Mechanik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.
Online-Hilfe für das Modul
zur Veranschaulichung der prinzipiellen Zusammenhänge, die bei Molekularbewegungen vorherrschen.
Weitere relevante Seiten zu diesem Programm
Themen und Stichworte zu diesem Modul:Moleküle - Kollision - Molekülbewegung - Molekulare Bewegung - Zusammenstoß - Animation - Darstellung - Teilchen - Bewegung - Zwischenmolekulare Kräfte - Molekularkräfte - Anziehung - Adhäsion - Adhäsionskräfte - Adhäsionskraft - Kohäsion - Kohäsionskräfte - Kohäsionskraft - Adsorption - Intermolekulare Kräfte - Anziehungskräfte - Tabelle - Berechnen - Formel - Bestimmen - Einführung - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Aufgaben - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Arten - Bedeutung - Was bedeutet - Erklärung - Einfach erklärt - Herleitung - Beweis - Eigenschaften - Formeln - Messen - Physik - Begriff - Begriffe - Diffusion - Diffusionsvorgänge - Diffusionsvorgang - Grundlagen - Wasser - Definition - Zusammenhangskraft - Oberflächenspannung - Oberflächenenergie - Bügelmethode - Abreißmethode - Graph - Bild |
 |  |
Molekularbewegung (Molekülbewegung)
Modul Molekularbewegung
Das Unterprogramm [Mechanik I] - [Molekularbewegung] veranschaulicht die prinzipiellen Zusammenhänge, welche bei der Bewegung von Molekülen vorherrschen.
Molekularbewegung - Abbildung 1
Molekularbewegung - Abbildung 2
Moleküle befinden sich aufgrund ihrer kinetischen Energie andauernd in Bewegung. Ihre Bewegungsgeschwindigkeit hängt von deren Aggregatzustand ab. Bei Gasen ist diese am höchsten, bei Flüssigkeiten wesentlich geringer und bei Festkörpern aufgund ihrer Kristallstruktur sehr gering. Sie bewegen sich untereinander auf geradlinigen Bahnen. Dieser Vorgang wird als Molekularbewegung bzw. Molekülbewegung (molekulare Bewegung) bezeichnet.
Moleküle sind durch eine Masse und eine Geschwindigkeit definiert, welche ihre kinetische Energie wiederspiegeln.
In diesem Modul wird deren Masse symbolisch durch die Größe der Moleküle dargestellt (großer Durchmesser - große Masse, kleiner Durchmesser - kleine Masse). Dargestellte Linien sind symbolisch als Richtungsvektoren für die momentane Geschwindigkeit, welche das Molekül (Teilchen) besitzt, anzusehen. Nach jeder Kollision (jedem Zusammenstoß) von Molekülen (bzw. mit dem Rand des Darstellungsbereichs) werden Richtung und Geschwindigkeit der an- bzw. zusammengestoßenen Moleküle erneut ermittelt und in Form von Richtungsvektoren dargestellt.
Programmbedienung
Durch die Aktivierung bzw. Deaktivierung der zur Verfügung stehenden Kontrollkästchen Richtungsvektoren rote Moleküle bzw. Richtungsvektoren blaue Moleküle kann die Darstellung der enstprechenden Richtungsvektoren an- bzw. abgeschaltet werden. Angehalten werden kann die Simulation durch eine Bedienung der Schaltfläche Stop. Eine erneute Bedienung dieses Schalters setzt die Darstellung der Animation fort.
Zwischenmolekulare Kräfte - Adhäsion - Kohäsion
1. Zwischenmolekulare Kräfte:
Die zwischen den Atomen (Ionen, Molekülen) von Stoffen wirkenden Kräfte werden als zwischenmolekulare Kräfte oder Molekularkräfte bzw. intermolekulare Kräfte bezeichnet. Deren Größe entscheidet über den Aggregatzustand des entsprechenden Stoffes. Bei festen Körpern und Flüssigkeiten bestimmen diese Kräfte das Volumen dessen.
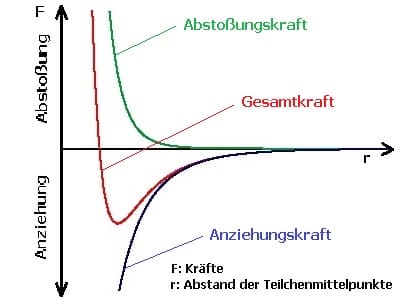
Um das Gleichgewicht zur Beibehaltung dieses Aggregatzustands aufrecht zu erhalten müssen die einzelnen Moleküle dieses Stoffes einen bestimmten Abstand (Normalabstand) zueinander besitzen. Ist der Abstand dieser Moleküle größer als der Normalabstand, so wirken diese zwischenmolekularen Kräfte gegenseitig anziehend, ist er hingegen größer, so wirken sie gegenseitig abstoßend. Kräfte dieser Art besitzen lediglich eine geringe Reichweite (Wirkungssphäre).
2. Köhäsion und Adhäsion:
Kräfte dieser Art, die zwischen den einzelnen Molekülen eines Körpers wirken, werden als Kohäsionskräfte bezeichnet. Als Adhäsionskräfte werden derartige Kräfte bezeichnet, die zwischen den Molekülen zweier verschiedener Körper wirken.
Mit Kohäsion wird der zwischen den Molekülen eines einzelnen Körpers herrschende Zusammenhang bezeichnet, der sich durch deren gegenseitige Anziehung ergibt.
Mit Adhäsion wird der zwischen den Molekülen zweier verschiedener Körper herrschende Zusammenhang bezeichnet, der sich bei Festkörpern oder Flüssigkeiten durch deren gegenseitige Anziehung ergibt.
Mit Adsorption wird der zwischen den Molekülen zweier verschiedener Körper herrschende Zusammenhang bezeichnet, der sich bei Gasen durch deren gegenseitige Anziehung ergibt.
Diffusion
Als Diffusion wird der stetige Ortswechsel von Molekülen bezeichnet, der aufgrund derer thermisch verursachten Bewegungen zustande kommt. Sie ist ein stark temperaturabhängiger Prozess, der bei Gasen aufgrund derer Beweglichkeit am stärksten auftritt. Bei Festkörpern verlaufen Diffusionsvorgänge sehr langsam, bei Gasen am schnellsten.
Oberflächenspannung - Oberflächenenergie
Die Oberflächenspannung ist eine aufrund von zwischenmolekularen Kräften auftretende Erscheinung, die sich dahingehend auswirkt, die Oberfläche von Flüssigkeiten gering zu halten. Sie ist Folge der Kohäsion. Die Oberfläche einer Flüssigkeit befindet sich stets unter Spannung. Sie ist die Ursache dafür, dass Flüssigkeiten spärische Gestalt annehmen, sofern keine anderen Kräfte auf sie einwirken.
Da sich die Abstände zwischen einzelnen Flüssigkeitsmolekülen aufgrund der Wärmebewegung stetig verändern, können auf Flüssigkeitsteilchen sowohl abstoßende wie auch anziehende Kräfte wirken. Flüssigkeiten versuchen ihre Oberfläche an der Grenze zu einem Gas so gering wie möglich zu halten. Da eine Kugel diesbezüglich die kleinste Oberfläche besitzt, bilden sich kugelförmige Flüssigkeitsoberflächen, bei welchen in Bezug zur Umgebung ein höherer Druck herrscht.
Ein sich an der Oberfläche befindendes Flüssigkeitsmolekül besitzt im Verhältnis zu anderen Flüssigkeitsmolekülen, die sich im Inneren der Flüssigkeit befinden, eine höhere Energie, da es auf weniger Moleküle trifft, mit denen es in Wechselwirkung treten kann. Es erfordert daher die Verrichtung einer Arbeit, um ein Molekül an die Oberfläche zu bringen. Die Energie die ein Teilchen an der Oberfläche einer Flüssigkeit besitzt, wird als Oberflächenenergie bezeichnet.
Das Verhältnis der verrichteten Arbeit und der daraus resultierenden Vergößerung der Oberfläche wird als Oberflächenspannung bezeichnet. Für sie gilt:
σ = ΔW / ΔA
σ: Oberflächenspannung [J/m² = N/m = kg/s²]
ΔW: Verrichtete Arbeit [J]
ΔA: Oberfläche [m²]
Messung der Oberflächenspannung:
Die Oberflächenspannung kann mit Hilfe der Bügelmethode (Abreißmethode) durchgeführt werden. Bei diesem Verfahren wird ein Bügel, in welchem sich ein dünner Draht befindet soweit in eine Flüssigkeit getaucht, bis dieser der Flüssigkeit benetzt wird. Die nach oben gerichtete Zugkraft des Bügels wird kontinuierlich erhöht. Hierauf wird der Bügel aus der Flüssigkeit gezogen.
Dieser zieht einen Flüssigkeitsfilm mit sich. Bei einer bestimmten Position dessen reißt der Flüssigkeitsfilm ab. Bevor dieser reißt kann aus den Abmessungen des Bügels sowie der Dichte der Flüssigkeit die Oberflächenspannung berechnet werden.
Hierbei gilt für die Oberflächenspannung:
Aus
σ = ΔW / ΔA = FΔs/(2lΔs)
folgt:
σ = F/(2l)
σ: Oberflächenspannung [J/m² = N/m = kg/s²]
F: Die zur Dehnung erforderliche Kraft [N]
l: Länge der Randlinie [m]
Δs: Weg bis zum Reißen des Flüssigkeitsfilms [m]
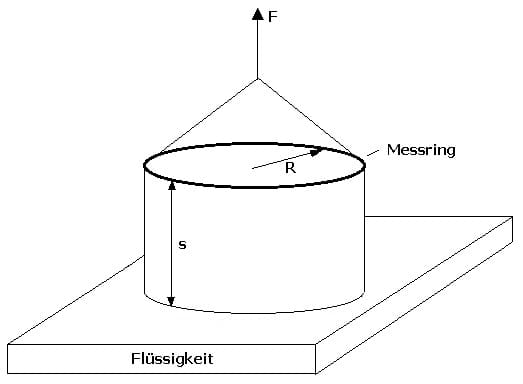
Da es sich bei dem im obigen Bild gezeigten um eine kreisförmige Randlinie handelt, gilt in diesem Fall:
σ = F/(4πR)
σ: Oberflächenspannung [J/m² = N/m = kg/s²]
F: Die zur Dehnung erforderliche Kraft [N]
R: Radius der kreisförmigen Randlinie [m]
In der folgenden Tabelle ist die Oberflächenspannung einiger Flüssigkeiten aufgeführt (wenn nicht anders angegeben, bei 20°C):
| Flüssigkeit | Oberflächenspannung in [mN/m] |
| Aceton | 23,3 |
| Benzol | 28,9 |
| Chloroform | 27,3 |
| Ethanol | 22,55 |
| Ethylenglycol | 48,4 |
| Ethanol | 22,3 |
| Essigsäure | 26,4 |
| Galinstan | 718 |
| Glycerin | 63,4 |
| Methanol | 22,6 |
| Nitrobenzol | 43,3 |
| Oktan | 21,8 |
| Petroleum (0°C) | 28,9 |
| Quecksilber | 476 |
| Schwefelsäure | 55,1 |
| Toluol | 28,5 |
| Wasser (20° C) | 72,75 |
| Wasser (50° C) | 67,9 |
| Wasser (80° C) | 62,6 |
| Wasser (100° C) | 58,8 |
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
4-Takt-Ottomotor - Impulssatz - Gleichförmige und gleichförmig beschleunigte Bewegung - Bewegung und Geschwindigkeit - Geschwindigkeit und Beschleunigung - Wellen - Druck in Flüssigkeiten - Ideale Strömung - Kinetische und potentielle Energie - Brownsche Bewegung - Harmonische Schwingungen - Kreisbahnbewegung - Auftrieb - Geneigte Ebene - Freier Fall - Waagerechter und schiefer Wurf - Pendel - Chaos-Doppelpendel - Gedämpfte mechanische Schwingung - Rolle und Flaschenzug - Balkenwaage - Hebelgesetz - Zweites Newtonsches Gesetz - Drittes Newtonsches Gesetz - Mechanische Arbeit - Hookesches Gesetz
Unterprogramm Molekularbewegung
PhysProf 1.1 - Unterprogramm RLC-Kreis
MathProf 5.0 - Unterprogramm Kurven in Parameterform
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Physik interaktiv
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
Eine Übersicht aller in MathProf 5.0 zur Verfügung stehender Programmteile finden Sie im MathProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
