PhysProf - Gase - Luftdruck - Höhenformel - Barometer

Fachthemen: Molekülgeschwindigkeit in Gasen - Luftdruck - Höhenformel
PhysProf - Thermodynamik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.

Online-Hilfe für das Modul
zur Auswertung des Verhaltens von Molekülgeschwindigkeiten in Abhängigkeit von der Temperatur.
Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden physikalischen Sachverhalte.
Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.

Weitere relevante Seiten zu diesem Programm

Themen und Stichworte zu diesem Modul:Moleküle - Geschwindigkeit - Gaskonstante - Boltzmann-Konstante - Mittlere quadratische Geschwindigkeit - Mittlere Geschwindigkeit - Verteilungsgesetz - Maxwell - Mittelwert - Molekülgeschwindigkeit - Wahrscheinlichste Geschwindigkeit - Mittlere kinetische Energie - Temperatur - Maxwellsche Geschwindigkeitsverteilung - Gasmoleküle - Geschwindigkeitsverteilung - Geschwindigkeitsbetrag - Mol - Avogadro-Konstante - Avogadro Konstante - Teilchenzahl - Teilchenanzahl - Avogadro Gesetz - Avogadrosches Gesetz - Satz von Avogadro - Molekülmasse - Molekulare Masse - Masse - Molare Masse - Molekül - Teilchen - Stoffmenge - Grundlagen - Luftdruck - Atmosphärischer Druck - Luft - Gas - Gase - Gasvolumen - Gasdruck - Druck in Gasen - Partialdruck - Partialdrücke - Teildruck - Teildrücke - Gesamtdruck - Überdruck - Innendruck - Außendruck - Unterdruck - Höhenformel - Barometrische Höhenformel - Internationale Höhenformel - Herleitung - Beweis - Formel - Formeln - Atmosphäre - Abhängigkeit - Meereshöhe - Normtemperatur - Normdruck - Normvolumen - Normdichte - Normbedingungen - Luftdruckmessung - Barometer - Messen - Quecksilberbarometer - Messung - Luftdruckanzeige - Begriff - Begriffe - Pascal - Bar - Torr - Definition - Einführung - Grundlagen - Dichte - Luftdichte - Dichte der Luft - Dichte von Luft - Druck - Luftdruckmesser - Luftdrucktabelle - Tabelle - Einheit - Einheiten - Pro - Höhe - Meter - Pa - kPa - km - m - Umrechnen - Umrechnung - Berechnen - Rechner - Verändern - Veränderung - Ändern - Änderung - Was - Wie - Weshalb - Was ist - Warum - Bedeutung - Was bedeutet - Erklärung - Einfach erklärt - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Aufgaben - Lösungen - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Beschreibung - Bild - Einheit - Physikalische Einheit - Grafik - Berechnung - Diagramm - Darstellen - Grafische Darstellung |
 |  |
Molekülgeschwindigkeit - Luftdruck - Höhenformel
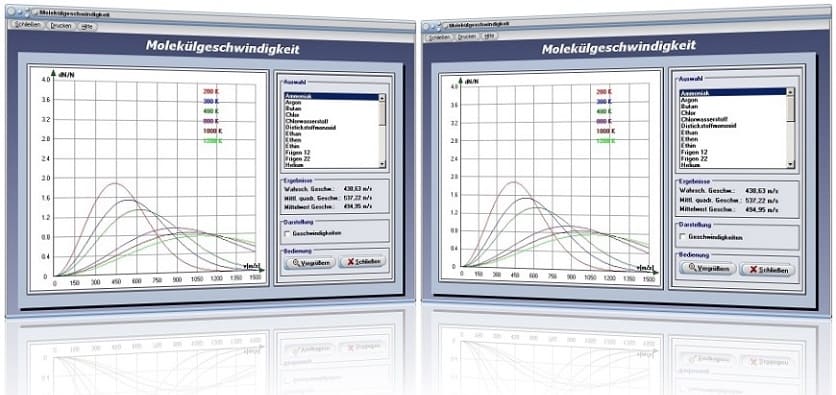
Modul Molekülgeschwindigkeit
Mit Hilfe des Unterprogramms [Thermodynamik] - [Molekülgeschwindigkeit] können die wahrscheinlichste und die mittlere Geschwindigkeit, sowie der Mittelwert der Geschwindigkeit sich bewegender Gasteilchen ermittelt werden.

Molekülgeschwindigkeit - Abbildung 1

Molekülgeschwindigkeit - Abbildung 2

Molekülgeschwindigkeit - Abbildung 3
Die Bewegung von Gasmolekülen erfolgt nach statistischen Gesetzen. Im zeitlichen Mittel besitzen alle Moleküle gleiche Energie und Geschwindigkeit. Zu bestimmten Zeitpunkten können Energie und Geschwindigkeit (Geschwindigkeitsbetrag) eines einzelnen Moleküls erheblich vom Mittelwert abweichen. Maxwell hat ein Verteilungsgesetz für Molekülgeschwindigkeiten entwickelt, mit welchen die relative Häufigkeit ermittelt werden kann, mit der sich Gasteilchen in Abhängigkeit von der Temperatur bewegen. Das Verteilungsgesetz nach Maxwell, welches auch als Maxwellsche Geschwindigkeitsverteilung bezeichnet wird, lautet:

Die wahrscheinlichste Geschwindigkeit kann hierbei ermittelt werden durch:

Der Verlauf der Verteilungsfunktion ist asymmetrisch. Die wahrscheinlichste Geschwindigkeit kann an der Lage des Maximums der Kurve erkannt werden. Mit zunehmender Temperatur nimmt die durchschnittliche Geschwindigkeit zu und die Verteilung wird breiter. Da bei Berechnungen dieser Art nicht von der Momentangeschwindigkeit eines einzelnen Moleküls ausgegangen werden kann, wird ein quadratischer Mittelwert für die Bewegungsgeschwindigkeit aller Moleküle ermittelt. Dieser wird bezeichnet als mittlere quadratische Geschwindigkeit:

Ein weiterer Mittelwert ergibt sich aus:

Hierbei sind:
N: Anzahl der Moleküle in einem Gas
dN: Anzahl der Moleküle mit einer Geschw. innerhalb eines best. Bereichs
v: Untere Grenze dieses Geschwindigkeitsbereichs [m/s]
dv: Größe des Geschwindigkeitsbereichs [m/s]
R: Gaskonstante [J/(kgK)]
T: Gastemperatur [K]
e: Eulersche Zahl
k: Boltzmann-Konstante = 1,381·10-23 J/K
mM: Masse eines Moleküls [kg]
Programmbedienung
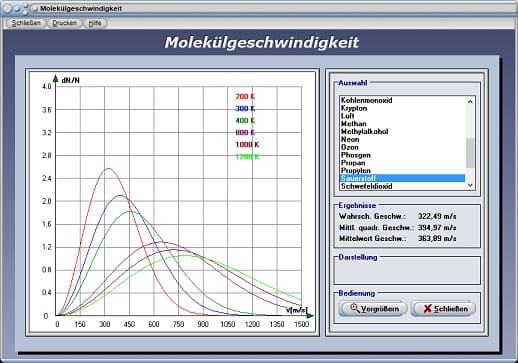
Das oben beschriebene Verhalten von Molekülgeschwindigkeiten in Abhängigkeit von der Temperatur können Sie untersuchen, indem Sie einen entsprechenden Eintrag in der zur Verfügung stehenden Liste fokussieren. Das Programm stellt daraufhin die Verteilungsfunktion für verschiedene Temperaturen dar.
Möchten Sie die Maxima der Funktion für eine Temperatur von 200 K (rote Kurve) eingezeichnet bekommen, so aktivieren Sie hierfür das Kontrollkästchen Geschwindigkeiten. Die angezeigten Bezeichnungskürzel haben folgende Bedeutung:
vw: Wahrscheinlichste Geschwindigkeit sich bewegender Gasteilchen
vm: Mittlere quadratische Geschwindigkeit sich bewegender Gasteilchen
vmw: Mittelwert der Geschwindigkeit sich bewegender Gasteilchen
Die im Fensterbereich Ergebnisse ausgegebenen Werte beziehen sich ausschliesslich auf die rot markierte Kurve für eine Temperatur bei 200 K.
Da der Darstellungsbereich bezüglich den Abszissenwerten erheblich variieren kann, steht der Schalter Vergrößern zur Verfügung, durch welchen Sie den Darstellungsbereich vergrößern bzw. verkleinern können.
Die mittlere kinetische Energie des Moleküls eines Gases beträgt:
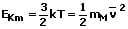
Die wahrscheinlichste kinetische Energie des Moleküls eines Gases beträgt:
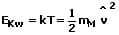
Die Temperatur eines Gases und die mittlere kinetische Energie eines Moleküls dessen sind proportional. Es gilt:
T ~ Ekm
Die zuvor aufgeführten Sachverhalte zur kinetischen Energie eines Moleküls gelten auch bei festen Stoffen und Flüssigkeiten.
Da die Dichte fester, flüssiger und gasförmiger Stoffe temperatur- und druckabhängig ist, wird diese unter Normbedingungen definiert. Diese sind wie folgt festgelegt:
Normtemperatur: Tn = 273,15 K (0 °C)
Normdruck: pn = 101325 Pa
Das Normvolumen ist eine Volumenmaßeinheit für das Gasvolumen die verwendet wird, um insbesondere Gasmengen bei unterschiedlichen Drücken und Temperaturen vergleichbar zu machen. Die Normdichte eines Gases (Stoffes) ist wie folgt definiert:
ρn = m/Vn
ρn: Normdichte des Gases (Stoffes) [kg/m³]
Vn: Normvolumen des Gases (Stoffes) [m³]
m: Masse des Gases (Stoffes) [kg]
In einem abgeschlossenen System mit einem sich darin befindenden Gas herrscht allerorts näherungsweise der gleiche Druck. Die von Gasmolekülen verursachten Stöße gegen die Wände des Systems erzeugen diesen. In einem mit einem Gas gefüllten abgeschlossenen System verhält sich der Druck proportional zur Temperatur des Gases. Ebensolches trifft auf das mittlere Quadrat der Geschwindigkeit der Gasmoleküle zu.
Es gilt:
p = nkT
bzw:
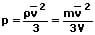
p: Druck des Gases [Pa]
m: Masse des Gases [kg]
V: Volumen des Gases [m³]
ρ: Dichte des Gases [kg/m³]
v: mittlere Geschwindigkeit des Gases [m/s]
n: Molekülzahldichte [1/m³]
T: Temperatur des Gases [K]
k: Boltzmann-Konstante = 1,381·10-23 J/K
Als Partialdruck (Teildruck) wird der Druck bezeichnet, der einem Gas (idealen Gasgemisch) zugerechnet werden kann. Der Gesamtdruck resultiert aus der Summe aller im System vorhandenen Teildrücke (Partialdrücke).
Nachfolgend sind einige Konstanten aufgeführt, welche sich auf die Masse und die Anzahl der Moleküle von Stoffen beziehen. 1 mol beinhaltet bei jedem beliebigen Stoff die gleiche Anzahl an Molekülen.
1. Avogadro:
Das Avogadrosche Gesetz (Avogadro Gesetz) besagt, dass alle Gase die die gleiche Temperatur und den gleichen Druck besitzen und sich in gleichen Volumna befinden, die gleiche Teilchenzahl (Teilchenanzahl) besitzen.
Die Avogadro-Konstante NA gibt die Anzahl der Moleküle (Teilchen) an, die sich in einem mol Stoffmenge eines Stoffes befinden. Sie entspricht der Anzahl der Moleküle N dividiert durch die Stoffmenge n in mol.
NA = N/n
oder
NA = 6,022137·1023/mol
2. Boltzmann-Konstante:
Die Boltzmann-Konstante k bildet sich aus dem Quotienten der molaren Gaskonstante Rm und der Avogadro-Konstante NA. Sie besitzt den Wert
k = Rm/NA = 8,31451 (J·mol) / 6,0221367·10-23 (mol·K) = 1,380649·10-23 J/K
3. Molekülmasse:
Die Molekülmasse oder molekulare Masse (Masse eines Moleküls) mM bildet sich aus dem Quotienten des Werts für die molare Masse M und der Avogadro-Konstante NA und berechnet sich somit wie folgt:
mM = M/NA = (M mol) / 6,0221367·1023
mit:
M in g/mol
mM in g
Luftdruck - Höhenformel
Unter einem Überdruck pü wird die Differenz zwischen einem Innendruck pabs und einem Außendruck (einem äußeren Luftdruck) pL verstanden. Ein Unterdruck pu entsteht, wenn der absolute Druck eines Gases pabs geringer ist als der äußere Druck (der äußere Luftdruck) pL. Die Messung des Luftdrucks (Gasdrucks) erfolgt mit Hilfe eines Manometers. Als Normdruck wird der Luftdruck bezeichnet, welcher in Meereshöhe bei einer Temperatur von 0°C herrscht. Der Normdruck trägt auch die Bezeichnung atmosphärischer Druck und beträgt 101 325 Pa = 1013,25 mbar = 760 Torr. Es gilt:
pü = pabs - pL
pabs: Absoluter Druck eines Gases [Pa]
pü: Überdruck
pL: äußerer Luftdruck
Luftdruck entsteht durch das Eigengewicht der Luft in seiner Umgebung (Hülle). Je größer der Abstand von der Erdoberfläche ist, desto geringer geringer wird der Luftdruck. Er reduziert sich mit zunehmender Höhe zunächst relativ stark, nimmt hierauf jedoch weniger ab. Ein Höhenunterschied von ca. 8 m verändert den Luftdruck um je 100 Pa.
Für den Luftdruck in Höhen bis zu ca. 100 km gilt bei konstanter Temperatur die barometrische Höhenformel:
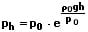
ph: Luftdruck in einer Höhe h [Pa]
p0: Luftdruck an der Erdoberfläche [Pa]
h: Höhe (Abstand von der Erdoberfläche) [m]
ρ0: Dichte der Luft (Luftdichte) an der Erdoberfläche [kg/m³]
e: Eulersche Zahl = 2,71828
g: Fallbeschleunigung = 9,81 m/s²
Wird für den Luftdruck am Boden für p0 der Wert 101,325 kPa verwendet und eine Atmosphärentemperatur von 0°C vorausgesetzt, so ergibt sich:
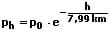
und hieraus:

Das nachfolgend dargestellte Diagramm bildet den Verlauf der Kurve der umgestellte barometrischen Höhenformel (siehe zuvor aufgeführte Formel) gemäß der Luftdrucktabelle ab.
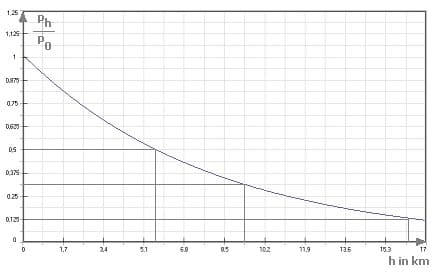
Da die Temperatur nicht konstant ist, sondern mit Zunahme der Höhe abnimmt wird für exaktere Bestimmungen die nachfolgend gezeigte internationale Höhenformel verwendet:
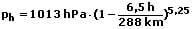
Diese berücksichtigt für pn einen Wert von 101,325 kPa sowie eine mittlere Jahrestemperatur von 15 °C und kann für Höhen bis zu 11 km Anwendung finden.
Luftdichte - Temperatur - Druck
Die Luftdichte ρ (Dichte der Luft bzw. Dichte von Luft) gibt an, welche Masse Luft in einem bestimmten Volumen enthalten ist.
Bei einer Temperatur von 20 °C beträgt die Dichte der Luft auf Höhe des Meeresspiegels ca. 1,2041 kg/m³. Ihre sich oberhalb dessen befindende Dichte ist geringer, da die darüber lastende Luftmasse mit zunehmender Höhe stets geringer wird. Flüssige Luft besitzt eine Dichte von 875 kg/m³.
Nachfolgend aufgeführte Tabelle zeigt die Luftdichte ρ in kg/m³ in Abhängigkeit von Temperatur t in °C und Druck p in hPa .
| t [°C] | p in [hPa] 960 | p in [hPa] 970 | p in [hPa] 980 | p in [hPa] 990 | p in [hPa] 1000 | p in [hPa] 1010 | p in [hPa] 1013 | p in [hPa] 1020 | p in [hPa] 1030 |
| 0 | 1,224 | 1,237 | 1,250 | 1,263 | 1,275 | 1,288 | 1,293 | 1,301 | 1,314 |
| 2 | 1,216 | 1,228 | 1,240 | 1,253 | 1,266 | 1,279 | 1,283 | 1,291 | 1,304 |
| 4 | 1,207 | 1,219 | 1,232 | 1,244 | 1,257 | 1,270 | 1,274 | 1,282 | 1,295 |
| 6 | 1,198 | 1,211 | 1,223 | 1,236 | 1,248 | 1,260 | 1,265 | 1,273 | 1,285 |
| 8 | 1,190 | 1,202 | 1,214 | 1,227 | 1,239 | 1,252 | 1,256 | 1,264 | 1,276 |
| 10 | 1,181 | 1,193 | 1,206 | 1,218 | 1,230 | 1,243 | 1,247 | 1,255 | 1,267 |
| 12 | 1,173 | 1,185 | 1,197 | 1,210 | 1,222 | 1,234 | 1,238 | 1,246 | 1,258 |
| 14 | 1,165 | 1,177 | 1,189 | 1,201 | 1,213 | 1,225 | 1,229 | 1,238 | 1,250 |
| 16 | 1,157 | 1,169 | 1,181 | 1,193 | 1,205 | 1,217 | 1,221 | 1,229 | 1,241 |
| 18 | 1,149 | 1,161 | 1,173 | 1,185 | 1,200 | 1,209 | 1,212 | 1,221 | 1,232 |
| 20 | 1,141 | 1,153 | 1,165 | 1,177 | 1,188 | 1,200 | 1,204 | 1,212 | 1,224 |
| 22 | 1,133 | 1,145 | 1,157 | 1,169 | 1,180 | 1,192 | 1,196 | 1,204 | 1,216 |
| 24 | 1,126 | 1,137 | 1,149 | 1,161 | 1,172 | 1,184 | 1,188 | 1,196 | 1,208 |
| 26 | 1,118 | 1,130 | 1,141 | 1,153 | 1,165 | 1,176 | 1,180 | 1,188 | 1,200 |
| 28 | 1,111 | 1,122 | 1,1134 | 1,145 | 1,157 | 1,168 | 1,172 | 1,180 | 1,192 |
| 30 | 1,103 | 1,115 | 1,1126 | 1,138 | 1,149 | 1,161 | 1,164 | 1,172 | 1,184 |
| 32 | 1,096 | 1,107 | 1,1119 | 1,130 | 1,142 | 1,153 | 1,157 | 1,165 | 1,176 |
| 34 | 1,085 | 1,098 | 1,110 | 1,122 | 1,135 | 1,147 | 1,151 | 1,159 | 1,172 |
Luftdruckmessung - Barometer
Der Luftdruck kann mittels einem Barometer (Luftdruckmesser) gemessen werden. Dieses beinhaltet das flüssige Metall Quecksilber, welches sich abhängig von der umgebenden Temperatur ausdehnt und zur Luftdruckmessung verwendet wird.
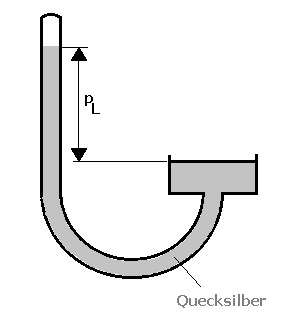
Es gilt:
p0 = pt(1- 0,000181·t/°C)
p0: Die auf 0°C reduzierte Luftdruckanzeige [Pa]
pt: abgelesener Luftdruck bei der Temperatur t [Pa]
t: Temperatur des Quecksilbers in °C
Molekülgeschwindigkeit - Abbildung 4

Molekülgeschwindigkeit - Abbildung 5
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Boltzmann-Verteilung sowie unter Wikipedia - Boltzmann-Konstante zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
Isochore Zustandsänderung - Isobare Zustandsänderung - Isotherme Zustandsänderung - Adiabatische Zustandsänderung - Carnotscher Kreisprozess - Aggregatzustände - Mischungsregel - Reales Gas
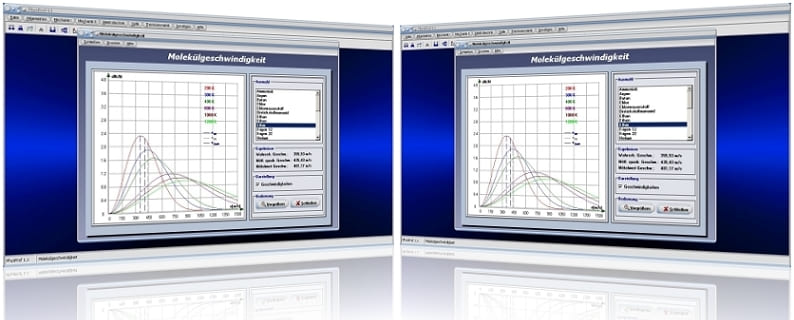
Unterprogramm Molekülgeschwindigkeit

PhysProf 1.1 - Unterprogramm RLC-Kreis

MathProf 5.0 - Unterprogramm Kurven in Parameterform

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
















