PhysProf - Kreisbahn - Zentripetalkraft - Rotation - Radialbeschleunigung
Fachthemen: Kreisbahn - Kreis - Rotation - Bewegung - Zentripetalkraft - Zentrifugalkraft
PhysProf - Mechanik - Kinematik - Eine Simulationssoftware zur Visualisierung physikalischer Sachverhalte mittels Computeranimationen zur Unterstützung des Unterrichts naturwissenschaftlicher Fächer und den Einsatz in MINT-Fächern als Ergänzung zum verwendeten Unterrichtsmaterial.
Online-Hilfe für das Modul
zur Analyse der Zusammenhänge, welche bei der Ausführung gleichförmiger Bewegungen und gleichförmig beschleunigter Bewegungen auf einer Kreisbahn vorherrschen.
Dieses Unterprogramm ermöglicht die Durchführung der Steuerung entsprechender Abläufe in Echtzeit, bietet die Möglichkeit, die Einflüsse relevanter Größen interaktiv zu untersuchen und eignet sich zudem als ergänzendes Unterrichtsmaterial zum Physikunterricht und Abitur.
Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.
Dieses Programm eignet sich unter anderem beim Abitur als Begleiter im Fach Physik und kann zur Erweiterung bereits erlangten Fachwissens in entsprechenden Themengebieten benutzt werden.
Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.
Themen und Stichworte zu diesem Modul: |
 |  |
Kreisbahnbewegung
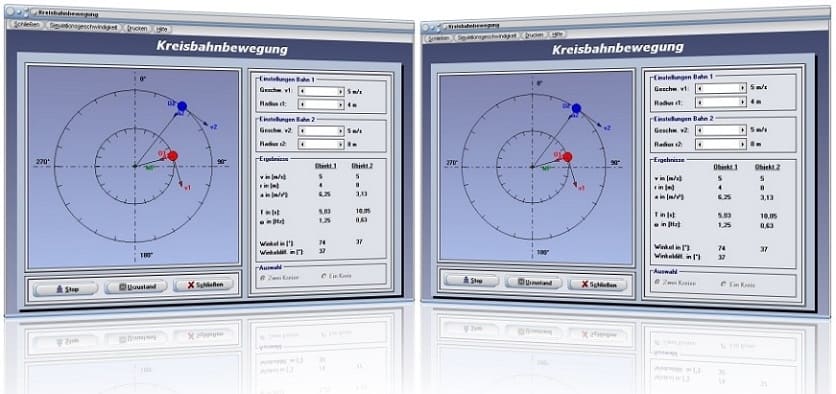
Modul Kreisbahnbewegung
Das Unterprogramm [Mechanik I] - [Kreisbahnbewegung] ermöglicht es, sich Zusammenhänge, welche bei gleichförmigen Bewegungen auf Kreisbahnen vorherrschen, zu verdeutlichen.
Kreisbahnbewegung - Abbildung 1
Kreisbahnbewegung - Abbildung 2
Kreisbahnbewegung - Abbildung 3
Kreisbahnbewegung - Abbildung 4
Kreisbewegungen: Eine Kreisbewegung (kreisförmige Bewegung) ist eine Bewegung, bei der die Bahnkurve auf einem Kreis verläuft. Der Betrag des Geschwindigkeitsvektors bleibt in diesem Fall konstant, nicht jedoch seine Richtung.
Als gleichförmige Rotationsbewegung (gleichförmige Kreisbewegung) wird eine Bewegung bezeichnet, bei welcher sich ein Körper mit einer konstanten Geschwindigkeit auf einer Kreisbahn bewegt (hierbei ändert sich die Richtung der Geschwindigkeit). Der Körper wird durch das Einwirken der Radialkraft kontinuierlich auf der Kreisbahn gehalten. Eine derartige Bewegung wird auch als Drehbewegung oder krummlinige Bewegung bezeichnet.
Hierbei führen alle im Drehmittelpunkt liegenden Massenelemente eines starren Körpers eine Bewegung auf einer Kreisbahn aus. Dies ist eine Umfangsbewegung. Ebensolches gilt für die Bewegung einer Punktmasse im Abstand r > 0 um eine Drehachse.
Bei einer fortlaufenden Bewegung auf einer Kreisbahn bewegt sich der Körper auf einer geschlossenen Kreisbahn und kehrt stets wieder an einen sich auf dieser Bahn befindenden Ort zurück. Er durchläuft jeden Punkt seiner ihm zugewiesenen Bahn jeweils einmalig in gleicher Richtung.
Die für einen Umlauf benötigte Zeit wird als Umlaufzeit (Umlaufdauer) T bezeichnet. Mit der Drehzahl (Umdrehungsfrequenz oder Umlauffrequenz bzw. Drehfrequenz) wird die Anzahl der Umdrehungen beschrieben, die innerhalb eines bestimmten Zeitraums ausgeführt werden. Sie ist der Kehrwert der Umlaufdauer.
Es gilt:
T = 1/n
bzw.
n = 1/T
n: Drehzahl [1/s]
T: Umlaufdauer [s]
Die Anzahl der Umdrehungen die innerhalb eines Zeitabschnitts auf einer Kreisbahn ausgeführt werden, wird als Umlaufzeit T bezeichnet. Hierbei gilt:
T = t/N = (N/t)·n
T: Umlaufzeit [s]
N: Anzahl der Umdrehungen je Zeitabschnitt
t: Zeit [s]
Der Drehwinkel beschreibt den Winkel auf der Kreisbahn, um welchen die Drehung ausgeführt wird. Eine vollständige Umdrehung entspricht dem Winkel von 360° (Gradmaß) bzw. 2π (Bogenmaß).
1 rad =180°/π = 57,295°
Als Winkelgeschwindigkeit (Rotationsgeschwindigkeit oder Drehgeschwindigkeit bzw. Kreisgeschwindigkeit) wird eine vektorielle Größe bezeichnet, die Auskunft darüber gibt, innerhalb welchen Zeitraums sich ein Kreiswinkel mit der Zeit um eine Achse ändert. Sie berechnet sich aus der Drehzahl n sowie der Umlaufzeit T. Für sie gilt:
ω = 2π·n = 2π/T
Sie kann ebenfalls bestimmt werden mit:
ω = v/r
ω: Winkelgeschwindigkeit [1/s]
v: Geschwindigkeit auf der Kreisbahn (Tangentialgeschwindigkeit) [m/s]
r: Radius der Kreisbahn [m]
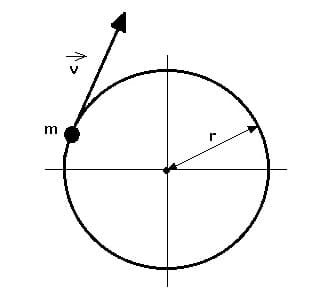
Als Umfangsgeschwindigkeit wird die Geschwindigkeit bezeichnet, die ein Massenpunkt besitzt, wenn dieser sich gleichförmig auf einer Kreisbahn bewegt.
Die Bahngeschwindigkeit beschreibt die Geschwindigkeit eines Objekts entlang eines Weges. In der Himmelsmechanik bezeichnet sie die Geschwindigkeit, mit der sich ein astronomisches Gebilde bewegt. Die Bahngeschwindigkeit eines einzelnen Punktes auf einer Kreisbahn (Kreisbahngeschwindigkeit) ist von dessen Abstand zur Rotationsachse (zum Mittelpunkt des Kreises) abhängig.
Der Geschwindigkeitsvektor beschreibt die Richtung und die Größe mit der sich ein auf einer Kreisbahn befindender Massenpunkt bewegt. Er wird auch als Geschwindigkeitspfeil bezeichnet.
Als Rotationsfrequenz (Kreisfrequenz oder Winkelfrequenz) wird die Anzahl voller Umdrehungen bezeichnet, die binnen einer Zeiteinheit ausgeführt wurden. Sie ist ein Maß dafür, wie schnell eine Drehung abläuft.
Als Periode wird das kleinste örtliche bzw. zeitliche Intervall bezeichnet, gemäß dem sich der Ablauf einer (physikalischen) Begebenheit wiederholt.
Umdrehungen pro Sekunde sind eine Einheit für die Winkelfrequenz. Es gilt: 1 Umdrehung pro Sekunde = 60 Umdrehungen pro Minute.
Durch die Winkelbeschleunigung wird die zeitliche Änderung der Winkelgeschwindigkeit beschrieben.
Programmmodul
In diesem Unterprogramm gelten für die entsprechenden Zusammenhänge bei gleichbleibender Rotationsgeschwindigkeit die nachfolgend aufgeführten Gesetzmäßigkeiten.
Die Bahngeschwindigkeit (Drehgeschwindigkeit) eines Körpers errechnet sich aus:
Dessen konstante Beschleunigung beträgt:
Die für eine Umdrehung benötigte Zeitdauer T (Umlaufdauer bzw. Umlaufzeit) ergibt sich aus:
Programmbedienung
Mit Hilfe dieses Unterprogramms können o.a. Sachverhalte untersucht werden.
Wird der Kontrollschalter Zwei Kreise aktiviert, so bewegen sich bei Ausführung einer Simulation zwei Massenpunkte mit konstanten Geschwindigkeitsbeträgen auf zwei (verschiedenen) Kreisbahnen. Dargestellt werden die Geschwindigkeitsvektoren der beiden Objekte. Das Programm ermittelt hierbei deren Kreisfrequenzen, deren Beschleunigungen, deren Umlaufdauern, sowie die Winkeldifferenzen, die diese Massen auf der zu durchlaufenden Kreisbahn besitzen und gibt diese aus. Legen Sie in diesem Fall zunächst mittels den zur Verfügung stehenden Rollbalken die Bahngeschwindigkeiten v1 und v2, sowie die Radien r1 und r2 der beiden Kreise fest.
Bei einer Aktivierung des Kontrollschalter Ein Kreis können oben aufgeführte Sachverhalte unter der Ausführung einer Simulation mit nur einem Kreis analysiert werden. Verwenden Sie hierbei die zur Verfügung stehenden Rollbalken um die konstante Bahngeschwindigkeit v, welche das Objekt auf der Kreisbahn besitzen soll, sowie dessen Radius r festzulegen. Das Programm gibt die Werte für Beschleunigung a des Massenpunkts, die Kreisfrequenz ω, sowie die für eine Umdrehung benötigte Zeitdauer T aus. Zudem wird die aktuelle Winkelposition des sich auf der Kreisbahn bewegenden Massepunkts angezeigt.
Bedienen Sie die Schaltfläche Start, so wird die entsprechende Bewegung ausgeführt. Durch die Bedienung der Schaltfläche Urzustand wird die Darstellung wieder in deren Anfangszustand versetzt.
Gleichförmige Rotation - Gleichmäßig beschleunigte Rotation
Nachfolgend dargestellt sind das φt-Diagramm sowie das ωt-Diagramm einer gleichförmigen Rotation (Drehbewegung). Die entsprechenden Schaubilder verdeutlichen die relevanten Zusammenhänge zu diesem Fachthema.
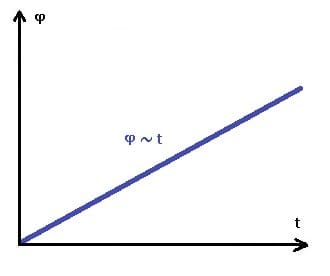
Gleichförmige Rotation - φt-Diagramm
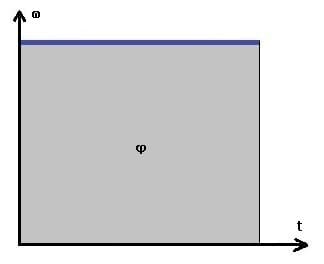
Gleichförmige Rotation - ωt-Diagramm
Gleichmäßig beschleunigte Rotation:
Als gleichmäßig beschleunigt wird eine Rotation bezeichnet, bei welcher die Beschleunigung des Körpers konstant ist. Nimmt die Rotationsgeschwindigkeit gleichmäßig zu, so ist die Beschleunigung positiv; nimmt sie ab, so ist sie negativ. Die Beschleunigung bei einer gleichmäßig beschleunigten Rotation ist konstant. Es gilt:
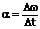
α: Winkelbeschleunigung [1/s²]
Δω: Änderung der Winkelgeschwindigkeit [1/s]
Δt: Zeit [s]
1. Gleichmäßig beschleunigte Rotation ohne Anfangsgeschwindigkeit:
Nimmt die Winkelgeschwindigkeit aus der Ruhelage heraus gleichmäßig zu, so gilt:
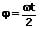
oder
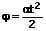
φ: Winkel, um welchen innerhalb der Zeit t gedreht wird [rad]
ω: Winkelgeschwindigkeit zur Zeit t [1/s]
α: Winkelbeschleunigung [1/s²]
t: Zeit [s]
Für die Winkelgeschwindigkeit gilt in diesem Fall:
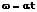
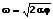
φ: Winkel, um welchen innerhalb der Zeit t gedreht wird [rad]
ω: Winkelgeschwindigkeit zur Zeit t [1/s]
α: Winkelbeschleunigung [1/s²]
t: Zeit [s]
Nachfolgend dargestellt sind das φt-Diagramm, das vt-Diagramm sowie das at-Diagramm einer gleichförmig beschleunigten Rotation ohne Anfangsgeschwindigkeit. Die entsprechenden Schaubilder verdeutlichen die relevanten Zusammenhänge zu diesem Fachthema. Bei den nachfolgend dargestellten Grafiken wird zugrunde gelegt, dass keine Anfangswinkelgeschwindigkeit vorhanden war.
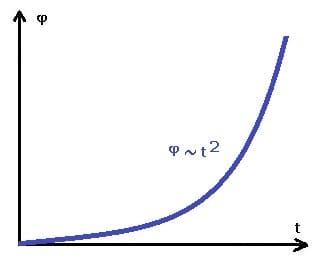
Gleichmäßig beschleunigte Rotation ohne Anfangsgeschwindigkeit - ωt-Diagramm
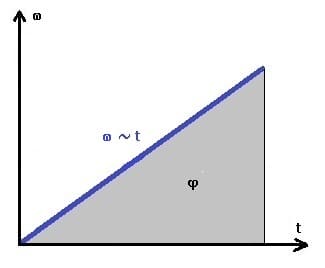
Gleichmäßig beschleunigte Rotation ohne Anfangsgeschwindigkeit - φt-Diagramm
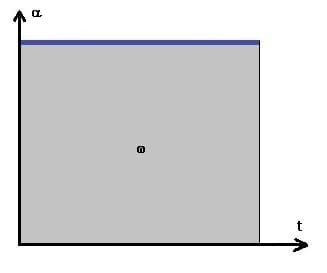
Gleichmäßig beschleunigte Rotation ohne Anfangsgeschwindigkeit - αt-Diagramm
2. Gleichförmig beschleunigte Rotation mit Anfangsgeschwindigkeit:
Ist eine Anfangswinkelgeschwindigkeit ω0 ohne bereits durchlaufenen Drehwinkel vorhanden, so gelten folgende Zusammenhänge:
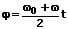
Wird der zur Zeit t0 bereits durchlaufene Drehwinkel ω0 berücksichtigt, so gilt:
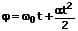
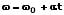
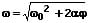
ω0: Anfangswinkelgeschwindigkeit [1/s]
ω: Winkelgeschwindigkeit zur Zeit t [1/s]
φ: Winkel, um welchen innerhalb der Zeit t gedreht wird [rad]
α: Winkelbeschleunigung [1/s²]
t: Zeit [s]
Nachfolgend dargestellt sind das φt-Diagramm, das ωt-Diagramm sowie das αt-Diagramm einer gleichförmig beschleunigten Rotation mit Anfangsgeschwindigkeit. Die entsprechenden Schaubilder verdeutlichen die relevanten Zusammenhänge zu diesem Fachthema. Bei den nachfolgend dargestellten Grafiken wird zugrunde gelegt, dass eine Anfangswinkelgeschwindigkeit vorhanden war.
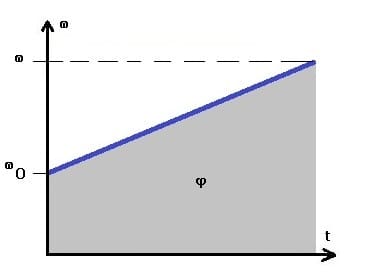
Gleichmäßig beschleunigte Rotation mit Anfangsgeschwindigkeit - ωt-Diagramm
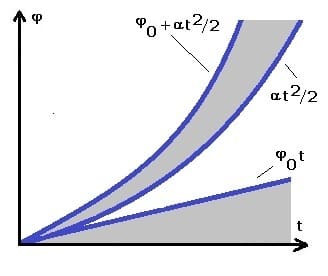
Gleichmäßig beschleunigte Rotation mit Anfangsgeschwindigkeit - φt-Diagramm
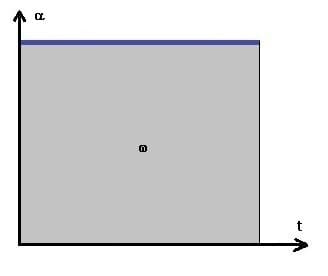
Gleichmäßig beschleunigte Rotation mit Anfangsgeschwindigkeit - αt-Diagramm
Gleichmäßig verzögerte Rotation
Als gleichmäßig verzögert wird eine Rotation bezeichnet, bei welcher die Beschleunigung des Körpers konstant ist und diese negativ ist. Eine Verzögerung unterscheidet sich von der Beschleunigung durch ihr negatives Vorzeichen.
Nachfolgend dargestellt sind das φt-Diagramm sowie das ωt-Diagramm einer gleichförmig verzögerten Drehbewegung.
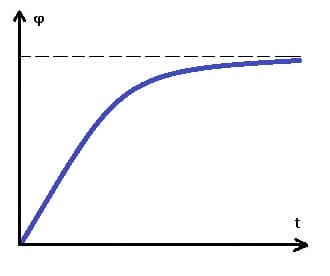
Gleichmäßig verzögerte Rotation - φt-Diagramm
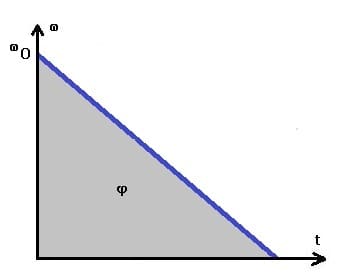
Gleichmäßig verzögerte Rotation - ωt-Diagramm
Mittlere Winkelgeschwindigkeit
Die mittlere Winkelgeschwindigkeit (durchschnittliiche Winkelgeschwindigkeit) beschreibt die Geschwindigkeit, die ein Objekt besessen hätte, wenn dieses über einen bestimmten Zeitraum hinweg mit gleichmäßiger Winkelgeschwindigkeit auf einer Kreisbahn bewegt worden wäre.
1. Ohne Anfangswinkelgeschwindigkeit:
Die mittlere Winkelgeschwindigkeit (Durchschnittswinkelgeschwindigkeit) einer gleichmäßig beschleunigten Drehbewegung ohne Anfangswinkelgeschwindigkeit kann wie folgt berechnet werden:
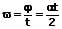
ϖ: Mittlere Winkelgeschwindigkeit [1/s]
φ: Winkel, um welchen innerhalb der Zeit t gedreht wird [rad]
α: Winkelbeschleunigung [1/s²]
t: Zeit [s]
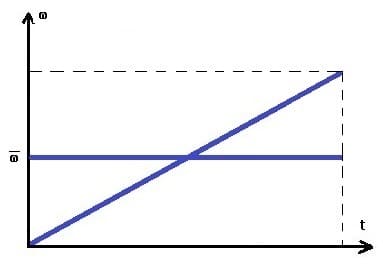
Mittlere Winkelgeschwindigkeit ohne Anfangswinkelgeschwindigkeit: ωt-Diagramm
2. Mit Anfangswinkelgeschwindigkeit:
Bei einer beschleunigten Rotationsbewegung mit Anfangswinkelgeschwindigkeit gilt:
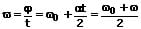
ϖ: Mittlere Winkelgeschwindigkeit [1/s]
ω0: Anfangswinkelgeschwindigkeit [1/s]
ω: Winkelgeschwindigkeit zur Zeit t [1/s]
φ: Winkel, um welchen innerhalb der Zeit t gedreht wird [rad]
α: Winkelbeschleunigung [1/s²]
t: Zeit [s]
Gilt es, ein zeitliches Intervall einer derartigen Bewegung unter der Berücksichtigung eines bereits vorhandenen Drehwinkels ω0 zu berechnen, so kann dies wie nachfolgend gezeigt erfolgen:
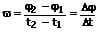
ϖ: Mittlere Winkelgeschwindigkeit [1/s]
t1,t2: Zeit [s]
φ1: Winkel, um welchen gedreht wird zur Zeit t1 [rad]
φ2: Winkel, um welchen gedreht wird zur Zeit t2 [rad]
Δt: Zeitdauer [s]
Δφ: Gesamtdrehwinkel, um welchen innerhalb des Zeitraums Δt gedreht wird [rad]
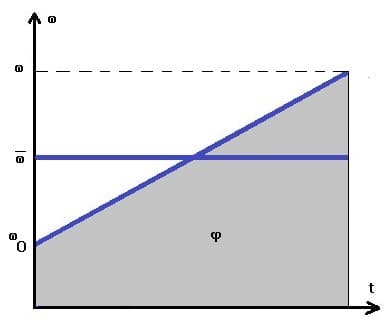
Mittlere Rotationsgeschwindigkeit mit Anfangsgeschwindigkeit: ωt-Diagramm
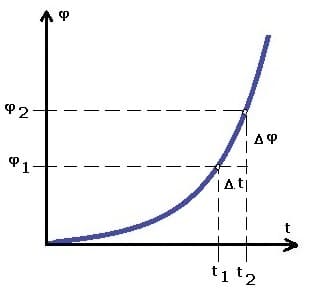
Mittlere Rotationsgeschwindigkeit mit Anfangsgeschwindigkeit: φt-Diagramm
Ungleichmäßig beschleunigte Rotation
Unter einer ungleichmäßig beschleunigten Rotation wird eine Bewegung verstanden, bei welcher die Änderung der Winkelgeschwindigkeit nicht proportional zur Zeit und die Beschleunigung nicht konstant ist. Die Winkelgeschwindigkeit, wie auch die Winkelbeschleunigung sind Funktionen der Zeit.
1. Für die momentane Winkelgeschwindigkeit gilt:
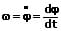
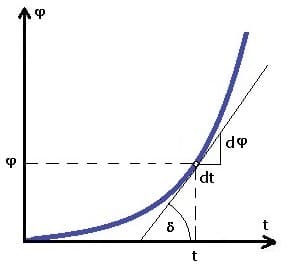
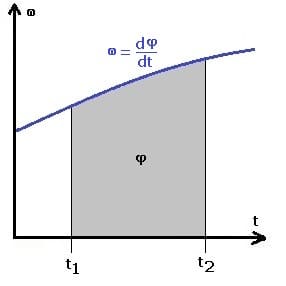
Sie ist die erste Ableitung der φt-Funktion nach der Zeit.
2. Für den zurückgelegten Weg bei einer ungleichmäßig beschleunigten Rotation gilt:
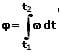
Der innerhalb eines Zeitraums zurückgelegte Weg wird als das Zeitintegral der Geschwindigkeit bezeichnet.
3. Für die momentane Winkelbeschleunigung gilt:
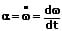
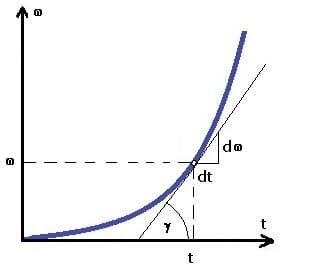
4. Die Winkelgeschwindigkeit wird als das Zeitintegral der Winkelbeschleunigung bezeichnet. Für sie gilt:
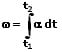
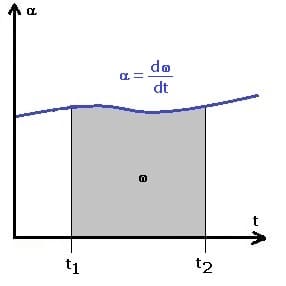
Arbeit und Leistung bei einer Drehbewegung
Arbeit bei einer Drehbewegung:
Für die bei einer Rotation eines Körpers verrichtete Arbeit bei konstantem Drehmoment gilt:
W = M·φ
W: Bei einer Rotation verrichtete Arbeit [J]
M: konstantes Drehmoment, welches die Rotation verursacht [Nm]
φ: Drehwinkel des Körpers [rad]
Ist das Drehmoment des rotierenden Körpers nicht konstant, so gilt:
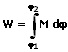
W: Bei einer Rotation verrichtete Arbeit [J]
M: Drehmoment, welches die Rotation verursacht [Nm]
Leistung bei einer Drehbewegung:
Die bei einer Drehbewegung erbrachte Leistung errechnet sich wie folgt:
P = M·ω
W: Bei einer Rotation erbrachte Leistung [W]
M: konstantes Drehmoment, welches die Rotation verursacht [Nm]
ω: Winkelgeschwindigkeit des Körpers [1/s]
Massepunkt - Starrer Körper
Ein Massepunkt (eine Punktmasse) ist als ein Modell zu interpretieren, bei dem die gesamte Masse eines Körpers in einem einzigen Punkt vereinigt ist. In vielen Fällen wird der Schwerpunkt (der Massenmittelpunkt) eines Körpers als Massepunkt festgelegt. Für einen Massenpunkt lassen sich lediglich Translationen ausführen.
Als starrer Körper wird ein idealisierter Körper in der Form eines Modells verstanden, der aus einzelnen Massenpunkten besteht, deren Abstände in jedem seiner Zustände unverändert bleiben. Er stellt ein System starr miteinander verbundener Massepunkte dar und Deformierungen einwirkender Kräfte werden in diesem Fall vernachlässigt. Anwendung findet dieses Modell stets dann, wenn man Form und Volumen des entsprechenden Körpers nicht außer Acht lassen kann. Entgegen dem Modell des Massepunkts können mit dem starren Körper auch Rotationsbewegungen ausgeführt werden.
Zentripetalkraft - Zentrifugalkraft - Trägheitskraft - Scheinkraft - Radialbeschleunigung - Zentripetalbeschleunigung - Starre Körper
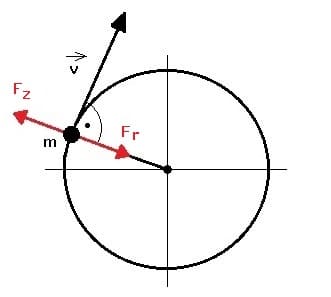
Bei der Bewegung einer Punktmasse oder des Massenpunkts eines starren Körpers auf einer Kreisbahn wirkt stetig eine zum Mittelpunkt des Kreises gerichtete Zentralbeschleunigung (Radialbeschleunigung oder Normalbeschleunigung) az, wenn eine zum Drehzentrum gerichtete Kraft wirkt. Diese Kraft wird als Zentripetalkraft Fr bezeichnet.
Als Zentrifugalkraft (Fliehkraft) Fz wird die Trägheitskraft (Scheinkraft) bezeichnet die vom Drehzentrum weg gerichtet wirksam ist. Beide dieser Kräfte sind entgegengesetzt gleich. Eine Trägheitskraft ist diejenige Kraft, die die Bewegung eines Körpers in einem beschleunigten Bezugssystem beschreibt. Unter einem starren Körper wird in der Mechanik ein idealisierter, nicht verformbarer Körper verstanden. Trägheitskräfte werden auch Scheinkräfte genannt.
Hinsichtlich des zuvor Beschriebenen gilt:
Fz = -Fr
Zentripetalkraft (Radialkraft):
Die Zentripetalkraft (Radialkraft), ist die zum Zentrum gerichtete Kraft, die einen Körper auf eine Kreisbahn zwingt. Es gilt:
Fr = m·v²/r = m·ω²·r
Zentrifugalkraft (Fliehkraft):
Bei der Zentrifugalkraft (Fliehkraft) handelt es sich um eine Trägheitskraft, die bei Rotations- und Kreisbewegungen auftritt und radial von der Rotationsachse ausgehend nach außen gerichtet ist. Sie kann wie folgt berechnet werden:
Fz = m·v²/r = m·ω²·r
Hierbei sind:
v: Geschwindigkeit [m/s]
ω: Kreisfrequenz [1/s]
a: Beschleunigung [m/s²]
r: Radius der Kreisbahn [m]
T: Dauer einer vollen Umdrehung [s]
FR: Zentripetalkraft
Fz: Zentrifugalkraft
Radialbeschleunigung (Zentripetalbeschleunigung):
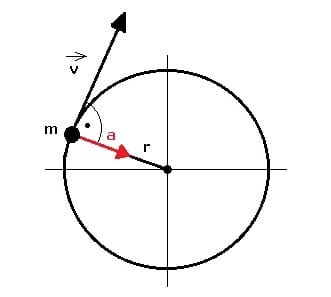
Bei der Radialbeschleunigung (Zentripetalbeschleunigung oder Normalbeschleunigung) handelt es sich um eine vektorielle Größe, welche Auskunft darüber gibt, in welchem Zeitraum sich die Geschwindigkeit bei einer Kreisbahnbewegung verändert. Sie ist stets zum Zentrum der Kreisbahn gerichtet. Es gilt:
ar = v²/r
oder:
ar = 4π2⋅r⋅n2
ar: Radialbeschleunigung [m/s²]
r: Radius der Kreisbahn [m]
n: Drehzahl [1/s]
Winkelbeschleunigung:
Als Winkelbeschleunigung wird die zeitliche Änderung der Winkelgeschwindigkeit eines sich drehenden Körpers bezeichnet. Sie ist eine vektorielle Größe. Für sie gilt:
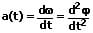
α: Winkelbeschleunigung [rad/s²]
ω: Winkelgeschwindigkeit [1/s]
φ: Winkel [rad]
t: Zeit [s]
Bahnbeschleunigung (Tangentialbeschleunigung):
Als Bahnbeschleunigung oder Tangentialbeschleunigung wird die Beschleunigung eines Punktes auf einer Bahn bezeichnet. Für sie gilt:
a = α·r
a: Bahnbeschleunigung (Tangentialbeschleunigung) [m/s²]
α: Winkelbeschleunigung [rad/s²]
r: Abstand des Punktes von der Rotationsachse [m]
Beschleunigung bei Kreisbahnbewegungen
In der nachfolgend gezeigten Übersicht (Tabelle) ist das Verhalten der Tangentialbeschleunigung at sowie der Radialbeschleunigung ar bei Kreisbahnbewegungen aufgeführt.
| Bewegungsart |
Tangential beschleunigung at | Radial beschleunigung ar |
| Gleichförmig | 0 | |
| Gleichmäßig beschleunigt | Bleibt konstant | Bleibt konstant |
| Ungleichmäßig beschleunigt | Verändert sich |
Corioliskraft - Coriolisbeschleunigung
Wenn sich ein Körper in dem rotierenden Bezugssystem radial nach außen oder innen vertikal zur Drehachse bewegt, so bewirkt diese eine Veränderung seiner Bahngeschwindigkeit. Er erfährt eine Tangentialbeschleunigung und wird aus diesem Grund im Bezugssystem auf einer kreisförmigen Bahn abgelenkt. Die Ursache dieser wird als Coriolis-Kraft bezeichnet. Diese Tangentialbeschleunigung wird Coriolis-Beschleunigung genannt.
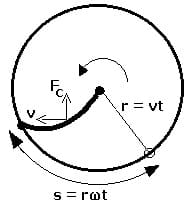
Der Weg des Körpers in Richtung des Radius r beträgt r = ωt. Im selben Zeitraum bewegt sich ein Punkt im Abstand r vom Drehzentrum auf der Strecke (dem Bogensegment) auf der Kreisbahn um die Strecke s = rωt weiter. Durch entsprechende Rechenoperationen kann aus diesen Zusammenhängen abgeleitet werden, dass die Coriolis-Beschleunigung dem nachfolgend gezeigten Sachverhalt genügt:
ac = 2vω
Der Betrag der wirkenden Coriolis-Kraft ergibt sich mit:
Fc = 2mvω
Vektoriell beschrieben lautet die Definition der Coriolis-Kraft:
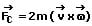
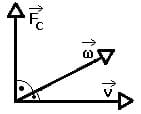
ac: Coriolis-Beschleunigung [m/s²]
v: Radialgeschwindigkeit des Körpers [m/s]
ω: Winkelgeschwindigkeit des rotierenden Bezugssystems [1/s]
m: Masse des rotierenden Körpers [kg]
Sind v und ω nicht konstant, so ergeben sich aus den oben gezeigten Formeln die momentan wirkende Coriolis-Kraft bzw. die momentane Coriolis-Beschleunigung.
Als Radialgeschwindigkeit wird bei einer Kreisbewegung die Komponente der Geschwindigkeit bezeichnet, die vom Zentrum des Kreises nach außen zeigt.
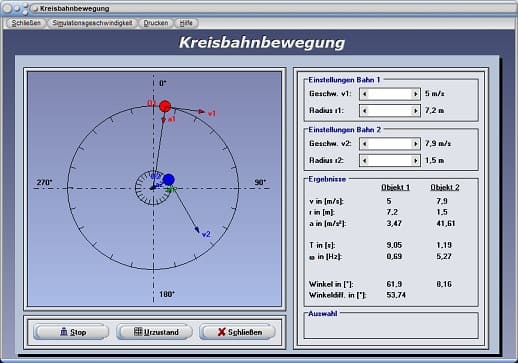
Kreisbahnbewegung - Abbildung 5
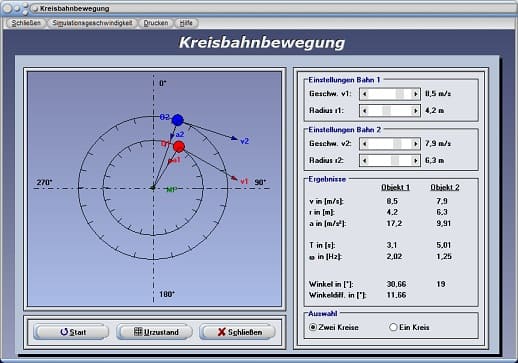
Kreisbahnbewegung - Abbildung 6
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Kreisbahnbewegung zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
4-Takt-Ottomotor - Impulssatz - Gleichförmige und gleichförmig beschleunigte Bewegung - Bewegung und Geschwindigkeit - Geschwindigkeit und Beschleunigung - Wellen - Druck in Flüssigkeiten - Ideale Strömung - Kinetische und potentielle Energie - Brownsche Bewegung - Molekularbewegung - Harmonische Schwingungen - Auftrieb - Geneigte Ebene - Freier Fall - Waagerechter und schiefer Wurf - Pendel - Chaos-Doppelpendel - Gedämpfte mechanische Schwingung- Rolle und Flaschenzug - Balkenwaage - Hebelgesetz - Zweites Newtonsches Gesetz - Drittes Newtonsches Gesetz - Mechanische Arbeit - Hookesches Gesetz
Unterprogramm Kreisbahnbewegung
PhysProf 1.1 - Unterprogramm RLC-Kreis
MathProf 5.0 - Unterprogramm Kurven in Parameterform
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Physik interaktiv
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
Eine Übersicht aller in MathProf 5.0 zur Verfügung stehender Programmteile finden Sie im MathProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
