PhysProf - Kondensatoren - Kapazität - Permittivität

Fachthema: Kondensator und Kapazität

PhysProf - Elektrotechnik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.

Online-Hilfe für das Modul
zur Berechnung von Kondensator-Kapazitäten.

Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.

 

Themen und Stichworte zu diesem Modul: Kondensatoren - Kapazität - Kapazitäten - Elektrische Kapazität - Kondensator - Arten - Relative Permittivität - Dielektrizitätskonstante - Permittivitätszahl - Dielektrizitätszahl - Elektrische Feldkonstante - Zweiplattenkondensator - Kugelkondensator - Zylinderkondensator - Kugel - Farad - Tabelle - Rechner - Doppelleitung - Doppelader - Zweidrahtleitung - Paralleldrahtleitung - Plattenabstand eines Kondensators - Eigenschaften - Berechnen - Berechnung - Dielektrikum - Formel - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Aufgaben - Was - Wie - Weshalb - Bedeutung - Begriff - Begriffe - Was bedeutet - Erklärung - Einfach erklärt - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Einführung - Übersicht - Formelzeichen - Platten - Kondensatorplatten - Permittivität - Konstanten - Geladene Körper - Fläche - Radius - Oberflächenladung

   

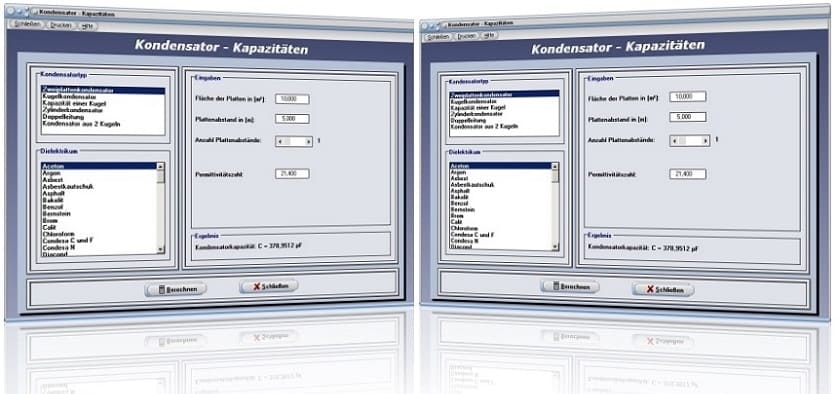
Modul Kondensator - Kapazitäten

---

 
Mit Hilfe des kleinen Unterprogramms [Elektrotechnik] - [Kondensator-Kapazitäten] können die Kondensatorkapazitäten verschiedener Kondensatortypen ermittelt werden
.

Kondensator - Kapazität - Abbildung 1


Kondensator - Kapazität - Abbildung 2
 

Kondensatoren sind zwei ungleichartig geladene Körper, welche einen bestimmten Abstand voneinander besitzen. Ihre Kapazität hängt von der Größe der Platten (Flächen), ihrem Abstand sowie dem Material zwischen den Platten (Dielektrikum) ab.
 
In diesem Modul können die Kapazitäten folgender Arten von Kondensatoren ermittelt werden:
 

• Zweiplattenkondensator
• Kugelkondensator
• Kapazität einer Kugel
• Zylinderkondensator
• Doppelleitung
• Kondensator aus zwei Kugeln

Elektrische Kapazität:

Die elektrische Kapazität (oder Kapazität) zwischen zwei voneinander isolierten elektrisch leitenden Körpern entspricht dem Verhältnis der zugeführten Ladungsmenge Q, die auf diesen Leitern gespeichert ist und der zwischen ihnen herrschenden elektrischen Spannung U. Ihre SI-Einheit ist das Farad [F]. Für sie gilt:

C = Q/U

C: elektrische Kapazität [F]
Q: elektrische Ladung [C]
U: elektrische Spannung [V]
 

Dielektrikum - Dielektrizitätszahl:

Ein Dielektrikum ist ein isolierendes Material. Die Dielektrizitätszahl ist die Konstante eines Materials, ausgedrückt als Verhältnis zur elektrischen Dielektrizitätskonstante des Vakuums.
 
Für die Dielektrizitätszahl gilt: ε_r = ε / ε₀
 
ε_r: Dielektrizitätszahl
ε: Permittivität [F/m]
e₀: Absolute Dielektrizitätskonstante e₀ = 8,85419·10^-12 As/Vm
 

Permittivität:

Die Permittivität (Dielektrizität, Dielektrizitätskonstante) ε gibt die Polarisationsfähigkeit eines Materials durch elektrische Felder an. Der Begriff Dielektrizität steht für die namensgebende Eigenschaft eines Dielektrikums(umgangssprachlich für die Permittivität ε).

Für die Permittivität gilt: ε = ε₀·ε_r
 

e_r: Relative Permittivität (Permittivitätszahl oder Dielektrizitätszahl)

e₀: Absolute Dielektrizitätskonstante (Elektrische Feldkonstante) e₀ = 8,85419·10^-12 As/Vm

 
Die elektrische Feldkonstante ist eine Naturkonstante, die zur Beschreibung elektrischer Felder Verwendung findet. Als relative Permittivität (Permittivitätszahl oder Dielektrizitätszahl) wird das Verhältnis der Permittivität eines Stoffes zur Permittivität eines Vakuums bezeichnet.
  

Arten von Kondensatoren - Kapazität

Nachfolgend aufgeführt sind die Arten der Kondensatoren für welche sich in diesem Unterprogramm entsprechende Berechnungen durchführen lassen. Dies sind der/die:
 

• Zweiplattenkondensator
• Kugelkondensator
• Kugel
• Zylinderkondensator
• Doppelleitung
• Kondensator aus zwei Kugeln

 

1. Zweiplattenkondensator:

Bei einem Zweiplattenkondensator handelt es sich um einen Kondensator, der aus zwei einander gegenüber angeordneten, voneinander isolierten Metallplatten besteht. Für ihn gilt:
 

mit e = e₀e_r
 

A: Fläche der Platten [m²]

d: Plattenabstand [m]

n: Anzahl der Plattenabstände

C: Kapazität [F]

 

2. Kugelkondensator:

Bei einem Kugelkondensator handelt es sich um einen Kondensator der aus zwei konzentrisch angeordneten Kugeloberflächen besteht, die gegenseitig isoliert sind und metallische Oberflächen besitzen. Für ihn gilt:
 

mit e = e₀e_r
 

A: Plattenoberfläche [m²]

r₁: Radius der Innenkugel [m]

r₂: Radius der Außenkugel [m]

C: Kapazität [F]

 

3. Kugel:
 

 

r: Radius der Kugel [m]

C: Kapazität [F]

 

4. Zylinderkondensator:

Ein Zylinderkondensator ist ein Kondensator, der aus zwei elektrisch leitenden Zylindermänteln (Rohren) besteht, zwischen welchen sich ein Dielektrikum befindet.
 

 

l: Länge des Zylinders [m]

r₁: Radius des inneren Zylindermantels [m]

r₂: Radius des äußeren Zylindermantels [m]

C: Kapazität [F]

 

5. Doppelleitung:

Bei einer Doppelleitung handelt es sich um zwei parallel angeordnete Leiter, die hinsichtlich ihrer Länge einen geringen Abstand zueinander besitzen. Sie besteht aus zwei Einzeladern, deren Leiterwerkstoff in der Regel Kupfer ist. Beide Einzeladern werden entweder miteinander oder mit zusätzlichen Adern verdrillt. Deren Abstand ist gegenüber ihrer Länge sehr gering. Zum Einsatz kommen Leitungen (Adern) dieser Art in der Nachrichtentechnik, in der Hochfrequenztechnik oder als Freileitungen. Für sie gilt:
 

 

l: Leitungslänge [m]

d: Abstand der Leitermitten [m]

r: Radius der Leiter [m]

C: Kapazität [F]
 

6. Kondensator aus zwei Kugeln mit gleichem Radius:

Hierbei handelt es sich um die Anordnung zweier metallischer Kugeln, die einen Abstand d zueinander besitzen. Für ihn gilt:
 

mit

und e = e₀e_r
 

C: Kapazität [F]

r: Kugelradien [m]

d: Kugelabstand [m]
 

Programmbedienung

 
Um die Kapazität eines oben aufgeführten Kondensatortyps ermitteln zu lassen, wählen Sie in der zur Verfügung stehenden Liste zunächst den entsprechenden Typ aus und geben daraufhin die für die Berechnung erforderlichen Werte in die dafür vorgesehenen Felder ein.

Die benötigte Permittivitätszahl können Sie entweder selbst in das dafür vorgesehene Feld eintragen, oder durch die Auswahl eines bestimmten Dielektrikums aus der dafür vorgesehen Listbox übernehmen. Das Programm trägt den entsprechenden Wert daraufhin selbst ein. Nach einer Bedienung der Schaltfläche Berechnung erhalten Sie das Ergebnis.
 

 
Nachfolgend aufgeführt sind die Werte für die Permittivität (Permittivitätszahl oder Dielektrizitätszahl) ε_r einiger Stoffe (bei 20°C und 50 Hz).
 

Medium	Permittivität εr   Dielektrizitätszahl
Aceton	21,5
Acrylglas	3
Aluminiumoxid	9
Ammoniak (0 °C)	1,007
Benzol	2,28
Chloroform	4,8
Germanium	16,6
Gips	2,65
Glas	6 ... 8
Glimmer	5 ... 8
Glycerin	42,5
Gummi	2,5 ... 3
Holz (trocken)	2 ... 3,5
Kaliumchlorid	4,94
Kohendioxid	1.000985
Luft	1,00059
Methanol	32,6
Nitrobenzol	35,5
Papier	1... 4
Paraffinöl	2,2
Petroleum	2
Polyethylen	2,4
Polypropylen	2,3
Polystyrol	2,5
Porzellan	5 ... 6,5
Propanol	18,3
Quarzglas	4
Sauerstoff	1,00486
Teflon	2
Toluol	2,38
Vakuum	1
Wasser	81

 
 

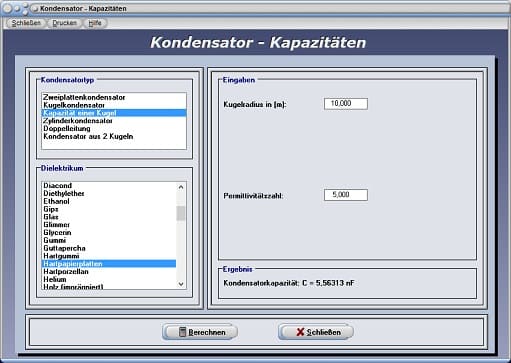
Kondensator - Kapazität - Abbildung 3


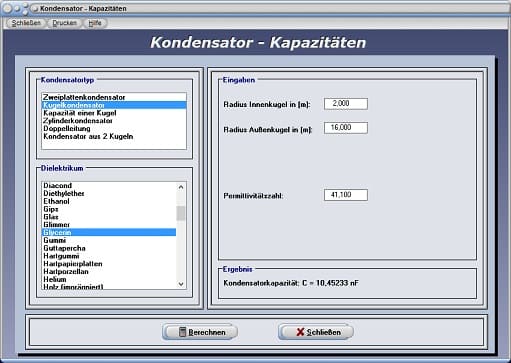
Kondensator - Kapazität - Abbildung 4
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden. Dieses Programm kann auch dabei behilflich sein, einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit. 

 
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.

 

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Elektrische Kapazität und unter Wikipedia - Kondensator zu finden.
 

 

Lissajousche Figuren - Reihen- und Parallelschaltung - Widerstände im Wechselstromkreis - Messbrücke - Widerstandsgesetz - Kondensator Ladung - Entladung - Plattenkondensator - Transformator - Schwingungsüberlagerung - RC-Kreis - RL-Kreis - RLC-Kreis - Resonanz - Wechselstromkreis
 

 

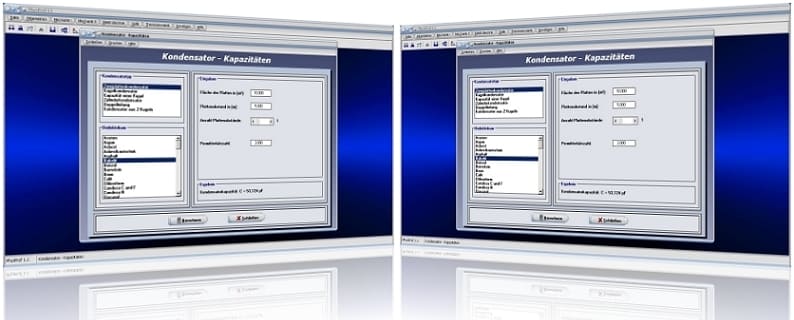
Unterprogramm Kondensator - Kapazitäten
 

 

PhysProf 1.1 - Unterprogramm RLC-Kreis
 

MathProf 5.0 - Unterprogramm Kurven in Parameterform
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

 

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

 
 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---