PhysProf - Keplersche Gesetze - Planetenbahnen - Gravitation

Fachthemen: Keplersche Gesetze - Gravitation

PhysProf - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.

Online-Hilfe für das Modul
zur grafischen Darstellung und Analyse der Zusammenhänge bzgl. der geltenden Keplerschen Gesetze.

Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden physikalischen Sachverhalte.

Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.

     

Themen und Stichworte zu diesem Modul: Keplersche Gesetze - Kepler Gesetze - 1. Keplersches Gesetz - 2. Keplersches Gesetz - 3. Keplersches Gesetz - Johannes Kepler - Planeten - Sonnenssystem - Planetenbewegung - Himmelskörper - Gesetze - Kosmische Geschwindigkeit - Kosmische Geschwindigkeiten - 1. Kosmische Geschwindigkeit - 2. Kosmische Geschwindigkeit - 3. Kosmische Geschwindigkeit - Orbitalgeschwindigkeit - Fluchtgeschwindigkeit - Entweichgeschwindigkeit - Grundlagen - Herleitung - Beweis - Satellit - Satelliten - Satellitenbahn - Anziehung - Körper - Himmelsmechanik - Bahngeschwindigkeit - Was - Wie - Weshalb - Was ist - Warum - Einführung - Bedeutung - Was bedeutet - Erklärung - Einfach erklärt - Beschreibung - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Aufgaben - Lösungen - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Begriff - Begriffe Anwendungsaufgaben - Bahn - Bahnen - Bahnkurven - Bahnformen - Gravitationsfeld - Keplerbahnen - Planetenbahn - Ellipsenbahn - Elliptische Umlaufbahn - Kraft - Gravitationskräfte - Gravitation - Anziehung - Kräfte - Antigravitation - Geschwindigkeit - Elliptische Bahn - Kreisbahn - Kreisbahngeschwindigkeit - Flächensatz - Abstand - Mittlere Entfernung - Entfernungsbestimmung - Planetensystem - Umlaufzeit - Umlaufzeiten - Umlaufdauer - Entfernung - Distanz - Planeten - Bestimmen - Berechnen - Formel - Formeln - Anziehungskraft - Newtonsches Gravitationsgesetz - Schwerkraft - Massenanziehung - Gravitationsgesetz - Gravitationskraft - Gravitationskonstante - Gravitationsbeschleunigung - Satellitengeschwindigkeit - Astronomische Einheit - Astronomische Einheiten - Parsec - Beispiel - Rechnen - Umlauf - Orbit - Massenverhältnis - Numerische Exzentrizität - Abstand - Distanz - Entfernung - Planet - Mittlere Entfernung - Entfernung Erde Mond - Entfernung Mond Erde - Entfernung Erde Mars - Entfernung Mars Erde - Erde - Pluto - Merkur - Neptun - Uranus - Saturn - Jupiter - Mars - Venus - Merkur - Umlaufdauer - Umlaufbahn - Rakete - Rechner - Erdumlaufbahn - Bild - Grafik - Simulation - Berechnung - Darstellen - Grafische Darstellung

   

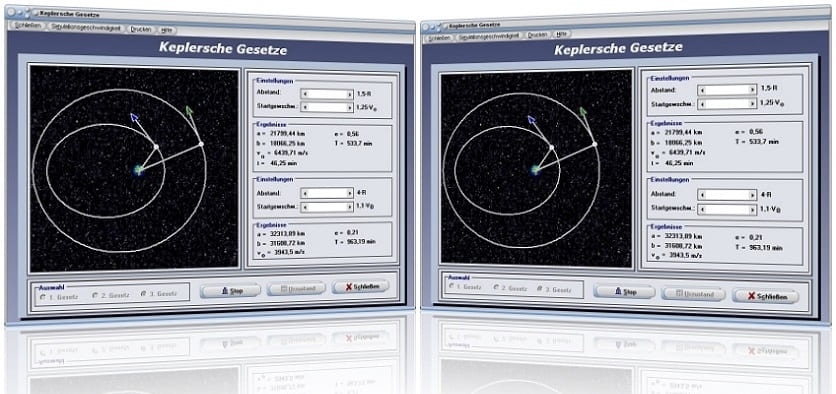
Modul Keplersche Gesetze

---

Mit Hilfe des Unterprogramms [Sonstiges] - [Keplersche Gesetze] wird es ermöglicht, sich Zusammenhänge der drei Gesetze von Kepler über Planetenbewegungen in unserem Sonnensystem verständlich zu machen.
 

1. Keplersches Gesetz
 

2. Keplersches Gesetz
 

3. Keplersches Gesetz
 

Der berühmte deutsche Astronom Johannes Kepler publizierte Anfang des 17. Jh. die nach ihm benannten Gesetze über Planetenbewegungen in unserem Sonnensystem.

1. Keplersches Gesetz:
 

Die Planeten bewegen sich auf Ellipsen in deren einem Brennpunkt die Sonne steht.

 

2. Keplersches Gesetz:
 

Die Verbindungsgerade von der Sonne zum Planeten überstreicht in gleichen Zeiträumen gleiche Flächen.

 

3. Keplersches Gesetz:
 

Das Verhältnis aus dem Quadrat der Umlaufzeit T und der dritten Potenz der großen Halbachse r der Planetenbahn ist für alle Planeten konstant.

Es gilt: r³/T² = const.
 

Die Keplerschen Gesetze sind nicht nur für die Bewegung von Planeten gültig, sondern sie können auch für die Bewegung von Raumfahrzeugen und Satelliten angewandt werden.

Bei der Flugbahn eines Satelliten, welcher sich in der Erdumlaufbahn befindet, kommen sowohl das Gravitationsgesetz als auch das Trägheitsgesetz von Newton zur Anwendung. Beide Kräfte wirken gleichermaßen; die Gravitation, welche ihn zum Erdmittelpunkt zieht, als auch die Trägheit, welche den einmal beschleunigten Satelliten ins All ziehen würde. Die Geschwindigkeit, bei welcher zwischen Gravitation und Zentrifugalkraft ein Gleichgewicht herrscht, beträgt ca. 7900 km/s. Es handelt sich hierbei um die erste kosmische Geschwindigkeit. Mit dieser Geschwindigkeit kann der Satellit die Erde auf einer kreisförmigen Bahn umfliegen. Erreicht die Geschwindigkeit eines Satelliten (die Satellitengeschwindigkeit) einen Wert von ca. 11200 km/s (2. kosmische Geschwindigkeit), so wird aus der Ellipsenbahn eine offene Parabel. Bei noch höheren Geschwindigkeiten nimmt die Flugbahn die Form einer Hyperbel an. In beiden Fällen kehrt das Raumfahrzeug nicht mehr zum Gravitationszentrum zurück. Auf elliptischen Flugbahnen ist die Geschwindigkeit des Flugkörpers abhängig von seinem Abstand zur Erde. Am erdnächsten Punkt (Perigäum) ist seine Geschwindigkeit am höchsten, am erdfernsten Punkt (Apogäum) ist sie am geringsten.
 

Programmbedienung

 
Mit Hilfe dieses Moduls können Sie sich die geltenden Zusammenhänge bezüglich der Keplerschen Gesetze anhand von Beispielen verdeutlichen, bei welchen sich ein Satellit um die Erde bewegt. Hierbei wird es ermöglicht, den Startpunkt des Satelliten bzgl. seines Abstandes zur Erde und seiner Startgeschwindigkeit einzustellen. Bei der Darstellung des ersten Keplerschen Gesetzes wird die Umlaufbahn eines Satelliten auf einer elliptischen Bahn um die Erde dargestellt. Der Erdradius beträgt (per Festlegung) R = 6388,23 km.

Hierbei werden die Werte für die Parameter der Ellipse (Haupt- und Nebenachse, Exzentrizität) und die Umlaufzeit (Umlaufdauer) T ausgegeben. Es ist u.a. auch möglich die Parameter so einzustellen, dass der Satellit die Umlaufbahn verlässt (hyperbolische Umlaufbahn).

Bei der Darstellung des zweiten Keplerschen Gesetzes wird veranschaulicht, dass die in einem gewissen Zeitraum überstrichenen Flächen der Ellipse gleich groß sind.

Das dritte Modell demonstriert zwei Satelliten, welche sich auf verschiedenen Umlaufbahnen befinden und diese gleichzeitig durchlaufen.

Durch die Aktivierung des entsprechenden Kontrollschalters 1. Gesetz, 2. Gesetz bzw. 3. Gesetz stellen Sie ein, zu welchem Keplerschen Gesetz Sie eine Animation dargestellt bekommen möchten.

Mittels der Bedienung des zur Verfügung stehenden Rollbalkens Abstand legen Sie den Faktor fest, welcher beschreibt in welchem Abstand von der Erde sich die Startposition des Satelliten befinden soll. Durch eine Positionierung des Rollbalkens Startgeschw. weisen Sie dem Satelliten die zu verwendende Startgeschwindigkeit zu.

Die vom Programm ausgegebenen Werte für a und b beschreiben die große und die kleine Halbachse der elliptischen Bahn auf welcher sich der Satellit bewegt. Die Zahl e beschreibt die Exzentrizität dieser elliptischen Bahn. Parameter T gibt Auskunft über die Dauer, die der Satellit benötigt um die festgelegte Umlaufbahn einmalig zu durchlaufen.

Eine Bedienung des Schalters Start ermöglicht die Durchführung einer Simulation. Bei Ausführung dieser zeigt das Programm die aktuelle Zeit t an, die seit Beginn des Durchlaufens auf der festgelegten Bahn verstrichen ist.
 

Entfernungsbestimmung - Entfernung - Planeten

 
Das dritte Keplersche Gesetz kann unter anderem zur Entfernungsbestimmung zweier Planeten eingesetzt werden, denn es gilt:



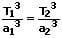
Durch Umformung resultiert hieraus für die Umlaufdauer (Umlaufzeit):



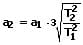
T₁,T₂: Umlaufdauer (Umlaufzeit) eines Planeten [a]
a₁,a₂: große Halbachse einer Planetenbahn [AE]
 
Beispiel:

Befinden sich die beiden Planeten Erde und Venus in sogenannter Konjuktionsstellung bzw. Oppositionsstellung zueinander, so können bei den vorliegenden Sachverhalten die Entfernungen dieser beiden Planeten wie folgt ermittelt werden:

Gegeben sind:

Halbachse Erde: a_Erde = 1 AE
Umlaufzeit: T_Venus = 0,61 a

Hinsichtlich der Umlaufdauer gilt in diesem Fall:



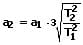
Durch das Einsetzen der entsprechenden relevanten Werte resultiert hieraus:



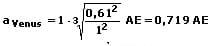
Hieraus kann entnommen werden, dass die Venus in Konjuktorstellung eine Entfernung von 1,719 AE zur Erde besitzt. In der Oppositionsstellung besitzt sie somit eine Distanz von 0,281 AE.
  

 
Isaac Newton (1643 - 1727) erkannte, dass die Kraft die den Mond in seiner Umlaufbahn um die Erde hält, dieselbe Kraft sein muss, die in gleicher Weise auf alle sich auf der Erde befindenden Körper wirkt. Sie wird als Gravitationskraft (Schwerkraft oder Anziehungskraft) bezeichnet und hängt von der Entfernung des Körpers vom Erdmittelpunkt ab. Er stellte fest: Der Betrag der Gravitationskraft nimmt mit dem Quadrat der Entfernung vom Erdmittelpunkt ab und diese Gesetzmäßigkeit lässt sich sinngemäß auf alle Himmelkörper anwenden.

Gravitation:

Mit dem Begriff Gravitation wird die Anziehung von Massen beschrieben. Sie trägt auch die Bezeichnung Massenanziehung oder Schwerkraft. Sie nimmt mit zunehmender Distanz der Massen ab.

Antigravitation:

Der Begriff Antigravitation ist die Bezeichnung einer Erscheinung bzw. einer Kraft, die entgegen der Gravitation wirksam ist. In Science-Fiction-Darstellungen und derartigen Romanen wird sie oftmals als Schutz vor Gravitation bzw. als eine der Gravitation entgegengesetzte Kraft beschrieben.




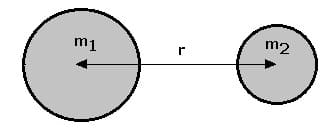
Als Gravitationskraft wird die zwischen zwei Körpern wirkende Anziehungskraft bezeichnet. Sie kann mit Hilfe des Newtonschen Gravitationsgesetzes bestimmt werden. Es gilt:
 

 
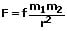
Der Betrag F der Gravitationskraft verhält sich umgekehrt proportional zum Quadrat des Abstandes der beiden Schwerpunkte der beiden Massen m₁ und m₂ sowie proportional zu diesen. Der Proportionalitätsfaktor f wird als Gravitationskonstante bezeichnet und besitzt den Wert f = 6,673·10^-11 m³/(kg²·s²).
 
F: Gravitationskraft [N]
m₁: Masse der Körpers 1 [kg]
m₂: Masse der Körpers 2 [kg]
r: Abstand der Schwerpunkte der beiden Körper [m]
f: Gravitationskonstante = 6,673·10^-11 m³/(kg²·s²)
 
Wird dieses Gesetz auf die Erde angewandt, werden für die beiden Massen m₁ und m₂ die Masse der Erde sowie die Masse des Körpers und für r der Abstand des Körpers vom Erdmittelpunkt eingesetzt, so gilt:


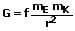
G: Gravitationskraft [N]
m_E: Masse der Erde [kg]
m_K: Masse des fallenden Körpers [kg]
r: Abstand der Schwerpunkte der beiden Körper [m]
f: Gravitationskonstante = 6,673·10^-11 m³/(kg²·s²)

Die Gravitationsbeschleunigung ist die Beschleunigung, die ein Körpers in einem Gravitationsfeld erfährt. Sie ist die Änderungsrate der Geschwindigkeit im Verhältnis zur Zeit aufgrund der Schwerkraft.
 
Astronomische Einheit:

Als Längenmaß wird in der Astronomie die Längeneinheit Astronomische Einheit (AE) verwendet. Sie dient zur Angabe von Entfernungen innerhalb des Sonnensystems und beträgt 149 597 870 700 Meter. Sie entspricht der mittleren Entfernung der Erde von der Sonne auf ihrer ellipsenförmigen Umlaufbahn  (der großen Halbachse).

Umrechnung:
1 AE = 149 597 870 700 Meter = 1,581 250 74·10⁻⁵ Lichtjahre = 4,848 136 81·10⁻⁶ Parsec
 
 

 
Als kosmische Geschwindigkeiten werden Geschwindigkeiten bezeichnet, die auf physikalischen Gegebenheiten beruhen, von besonderer Bedeutung sind und bei der Himmelsmechanik Gültigkeit besitzen.



Bei kosmischen Geschwindigkeiten wird zwischen drei dieser Art unterschieden. Es handelt sich hierbei um die

- 1. kosmische Geschwindigkeit (Keisbahngeschwindigkeit)
- 2. kosmische Geschwindigkeit (Fluchtgeschwindigkeit)
- 3. kosmische Geschwindigkeit (notwendige Geschwindigkeit zum Verlassen unseres Sonnensystems)

Die 1. kosmische Geschwindigkeit (die Keisbahngeschwindigkeit) ermöglicht es, die Geschwindigkeit zu berechnen, die notwendig ist um auf eine Kreisbahn um den entsprechenden Himmelskörper zu gelangen (Mindestgeschwindigkeit). Beispielsweise kann diese zur der Berechnung der Kreisbahngeschwindigkeit eines Erdsatelliten in beliebiger Höhe zum Einsatz kommen.

Bei der 2. kosmischen Geschwindigkeit (der Fluchtgeschwindigkeit) handelt es sich um die Geschwindigkeit, die erforderlich ist um das Gravitationsfeld eines Himmelskörpers (der Erde) zu verlassen (und sich unendlich weit von diesem zu entfernen).
 
Die 3. kosmische Geschwindigkeit ist diejenige Geschwindigkeit, die erforderlich ist um unser Sonnensystem zu verlassen.


Für die erste kosmische Geschwindigkeit (Fluchtgeschwindigkeit aus der Erdumlaufbahn) gilt:


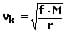
mit:

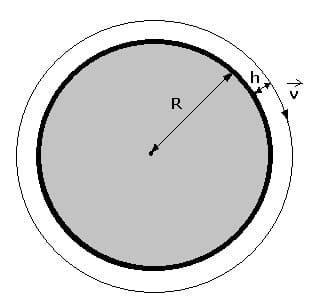
r = R+h

Für eine Kreisbahn an der Erdoberfläche beträgt diese v_k = 7,9 km/s.

v_k: Kreisbahngeschwindigkeit [m/s]
r: Radius der Bahn des Körpers (Satelliten) [m]
h: Abstand (Höhe) des Körpers (Satelliten) von der Erdoberfläche (Planetenoberfläche) [m]
R: Radius der Erde [m]
M: Masse der Erde (des Himmelskörpers) [kg]
f: Gravitationskonstante = 6,673·10^-11 m³/(kg²·s²)

Für die zweite kosmische Geschwindigkeit (Fluchtgeschwindigkeit aus dem Sonnensystem) gilt:


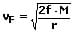
Für einen Punkt der Erdoberfläche (bei r = R) beträgt diese v_f = 11,2 km/s.

v_f: Fluchtgeschwindigkeit [m/s]
r: Abstand des Startorts vom Erdmittelpunkt (Mittelpunkt des Himmelskörpers) [m]
M: Masse der Erde (des Himmelskörpers) [kg]
f: Gravitationskonstante = 6,673·10^-11 m³/(kg²·s²)

Für die dritte kosmische Geschwindigkeit gilt:


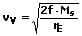
Wird die Sonne als Zentralkörper und die Erdoberfläche als Startpunkt gewählt, so beträgt diese v_v = 16 km/s.

v_v: Fluchtgeschwindigkeit [m/s]
r: Radius der Erdbahn = 149 598 022 960 m
M: Masse der Sonne (1,99·10³⁰ kg)
f: Gravitationskonstante = 6,673·10^-11 m³/(kg²·s²)

 
 

 

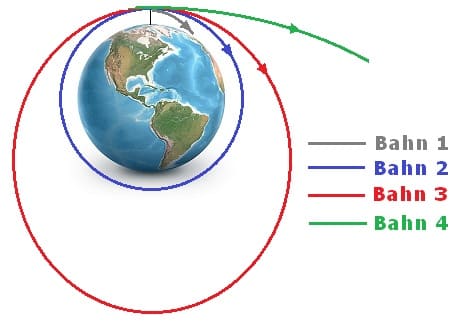
Wird von einem Planeten (außerhalb dessen Atmosphäre) ein Körper parallel zu dessen Oberfläche abgeschossen, so kann dieser abghängig von dessen Geschwindigkeit die folgenden Bahnkurven (Bahnformen) beschreiben:

Bahn 1: Parabel (bei kleinen Geschwindigkeiten)
Bahn 2: Kreisbahn (ausreichende Geschwindigkeit: v_Flucht/√2)
Bahn 3: Ellipsenbahn (ausreichende Geschwindigkeit: v < v_Flucht)
Bahn 4: Hyperbelbahn (ausreichende Geschwindigkeit: v > v_Flucht)

Die Winkelabhängigkeit des Radius r einer Bahnkurve hängt vom Abstand des Bahnpunkts vom Schwerpunkt ab: Es gilt:

r(ν) = p/(1+ε·ν)

r: Abstand des Bahnpunkts vom Schwerpunkt F
p: Halbparameter
ν: wahre Anomalie (Winkel)
ε: numerische Exzentrizität

Die numerische Exzentrizität ε beschreibt die Streckung der Bahn mit:

ε = 0: Kreisbahn
ε < 1: elliptische Bahn
ε = 1: parabolische Bahn
ε > 1: hyperbolische Bahn

 

Planeten unseres Sonnensystems

 
Tabelle einiger Eigenschaften der Planeten unseres Sonnensystems.
 

Planet	Mittlere Entfernung von Sonne [in106m]	Numerische Exzentrizität	Umlaufzeit [Jahre]	Massenverhältnis zu Erde
Merkur	57,92	0,2056	0,241	0,0558
Venus	108,1	0,0068	0,615	0,8148
Erde	149,6	0,0167	1	1
Mars	227,8	0,0934	1,881	0,1078
Jupiter	778,3	0,0485	11,86	317,82
Saturn	1427	0,0556	29,46	95,11
Uranus	2870	0,0472	84,02	14,52
Neptun	4495	0,0086	164,79	17,22
Pluto	5947	0,2534	250,61	0,00258

 

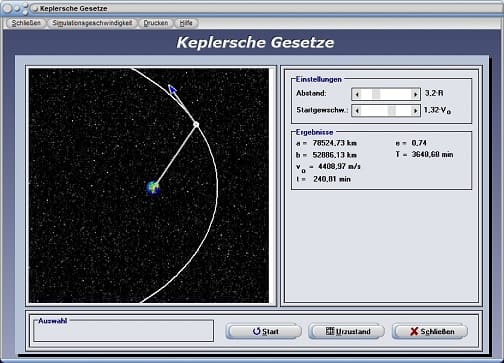
Keplersche Gesetze - Abbildung 1


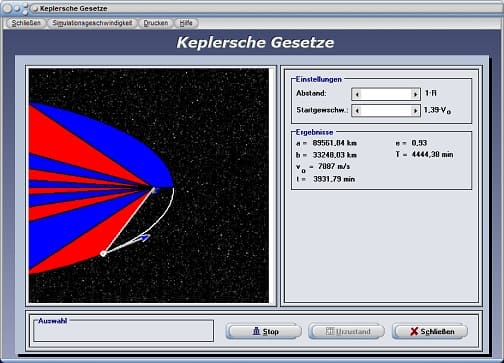
Keplersche Gesetze - Abbildung 2


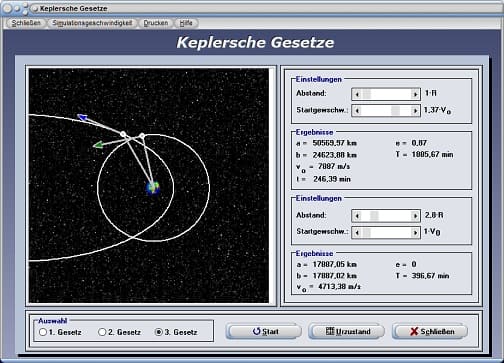
Keplersche Gesetze - Abbildung 3
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
 

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.

 

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Keplersche Gesetze sowie unter Wikipedia - Johannes Kepler zu finden.
 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

Formelbibliothek - Raumgittermodelle - Schalenbelegung-Orbitalbelegung - Bohrsches Atommodell - Kalender
 

 

Unterprogramm Keplersche Gesetze
 

 

PhysProf 1.1 - Unterprogramm RLC-Kreis
 

MathProf 5.0 - Unterprogramm Kurven in Parameterform
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

 

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

 
 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---