PhysProf - Impulssatz - Elastischer Stoß - Unelastischer Stoß

Fachthemen: Impulssatz - Stoß
PhysProf - Dynamik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.

Online-Hilfe für das Modul
zur Simulation des elastischen und unelastischen Stoßes.
Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden physikalischen Sachverhalte.
Es eignet sich zudem als Begleitung zu Versuchen im Physikunterricht, unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul: |
 |  |
Impulssatz
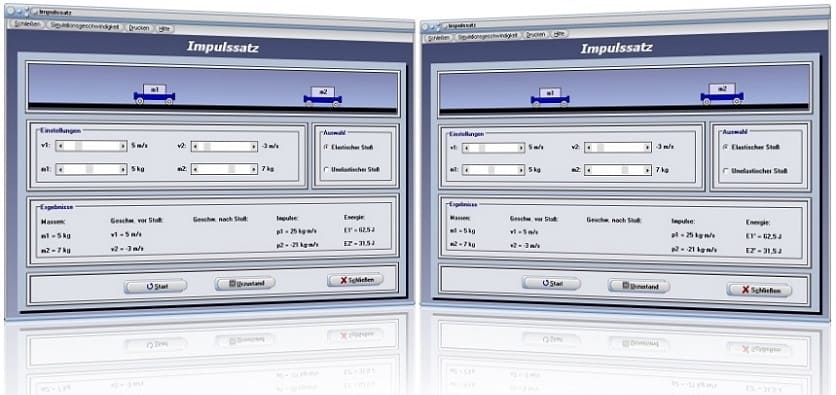
Modul Impulssatz
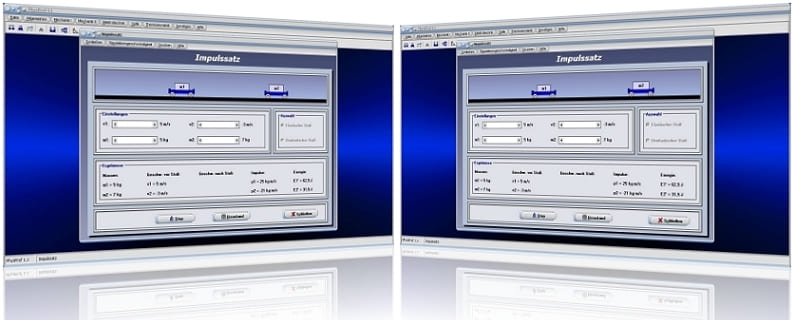
Das Unterprogramm [Mechanik I] - [Impulssatz] ermöglicht die Simulation des elastischen und des unelastischen Stoßes.

Impulssatz - Elastischer Stoß - Abbildung 1

Impulssatz - Unelastischer Stoß - Abbildung 2

Impulssatz - Unelastischer Stoß - Abbildung 3
Definition der Dynamik: In der Physik wird mit Hilfe der Dynamik die Wirkung von Kräften behandelt. Sie ist ein Teilgebiet der Mechanik und beschreibt die Bewegung von Körpern in Abhängigkeit der auf sie einwirkenden Kräfte. Sie gliedert sich in die wesentlichen Themenbereiche Statik (ruhende Körper) und Kinetik (Änderung der Bewegungsgrößen). Hierzu zählt auch das nachfolgend behandelte Thema Impulssatz.
Als Stoß wird der Zusammenprall (der Zusammenstoß bzw. der Aufprall oder die Kollision) zweier Körper beschrieben. Dies geschieht beispielsweise bei der Kollision zweier Kugeln. Während derer Berührung findet ein Energie- und Impulsaustausch statt. Bei einem Stoßprozess berühren sich zwei (oder auch mehrere) Körper kurzzeitig unter Änderung ihres jeweiligen Bewegungszustands.
Beim elastischen wie beim unelastischen Stoß gelten sowohl der Energieerhaltungssatz (Energiesatz), wie auch der Impulserhaltungssatz. Als Erhaltungssatz bezeichnet man in der Physik die Formulierung der beobachteten Tatsache, dass sich der Wert einer Größe, Erhaltungsgröße genannt, in bestimmten physikalischen Prozessen nicht ändert.
Unter dem Impuls eines Körpers wird das Produkt seiner Masse und seiner Geschwindigkeit verstanden. Der Impuls wird umgangssprachlich auch als Wucht bezeichnet. Der Impuls ist wie folgt definiert:

p: Impuls des Körpers [kg·m/s]
m: Masse des Körpers [kg]
v: Geschwindigkeit des Körpers [m/s]
Der Gesamtimpuls eines abgeschlossenen Systems ist konstant. Es gilt der Impulserhaltungssatz, welcher wie folgt definiert ist:

Dieser Satz wird auch als Impulserhaltung oder Impulssatz bezeichnet.
Aufgrund des Prinzips der Impulserhaltung bedeutet dies, dass der Gesamtimpuls mehrerer erfolgter Einzelimpulse kostant ist. Der Gesamtimpuls bildet sich aus der Summe aller erfolgter Impulse, verursacht durch die daran beteiligten Körper.
Bei einem zentralen Stoß verläuft die Verbindungsgerade der Schwerpunkte beteiligter Körper vertikal zu deren Berührfläche. Ist diese Bedingung bei der Ausführung eines Stoßes nicht erfüllt, so handelt es sich um einen nicht zentralen Stoß. Ein derartiger Stoß trägt auch die Bezeichnung dezentraler Stoß oder nicht zentraler Stoß.
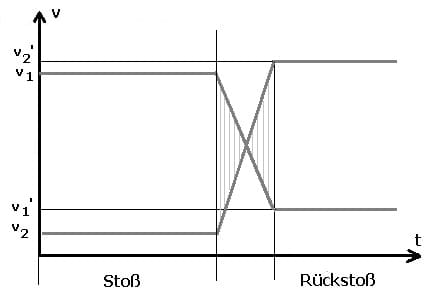
Als Rückstoß wird diejenige Gegenreaktion bezeichnet, die eintritt, wenn die Beschleunigung einer Masse erfolgt. Seine Richtung ist die dieser Beschleunigung entgegengesetzte Richtung. Er stellt diejenige Kraft dar, die auf einen Körper einwirkt, wenn eine Masse von ihm abgestossen wird.
Als Verformungsarbeit wird die Arbeit bezeichnet, die verrichtet wird, wenn auf einen Körper eine Kraft wirkt und dieser sich hierbei verformt.
I - Elastischer Stoß
Elastischer (zentraler elastischer) Stoß:
Beim elastischen Stoß (gerade, zentral) besitzen beide Körper nach dem Zusammenprall, nach Betrag und Richtung, veränderte Geschwindigkeiten. Bei einem geraden zentralen Stoß bewegen sich die Massenmittelpunkte beider Körper auf einer gemeinsamen Geraden. Dieser Stoß wird auch als gerader elastischer Stoß bzw. zentraler gerader elastischer Stoß bezeichnet.
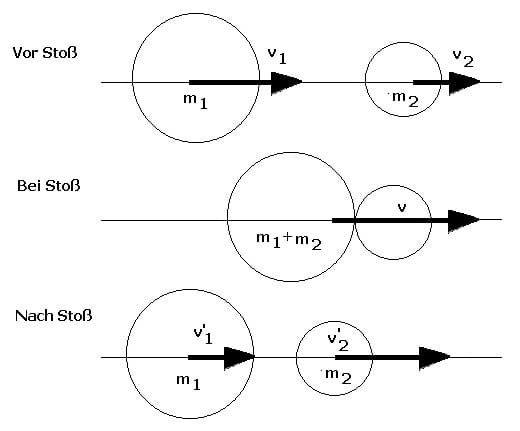
Es gilt nach dem Impulssatz:

und nach dem Energiesatz:

und hieraus:

und aus diesen Zusammenhängen:


Hierbei sind:
m1: Masse des Körpers 1 [kg]
m2: Masse des Körpers 2 [kg]
v1: Geschwindigkeit des Körpers 1 vor dem Stoß [m/s]
v2: Geschwindigkeit des Körpers 2 vor dem Stoß [m/s]
v1': Geschwindigkeit des Körpers 1 nach dem Stoß (Rückstoß) [m/s]
v2': Geschwindigkeit des Körpers 2 nach dem Stoß (Rückstoß) [m/s]
II - Unelastischer Stoß
Unelastischer (zentraler unelastischer) Stoß:
Sind die bei einem Stoßvorgang beteiligten Körper unelastisch, so verformen sie sich an ihren Berührungsstellen und bewegen sich daraufhin mit gemeinsamer Geschwindigkeit weiter. Beim unelastischen Stoß wird ein Teil der Gesamtenergie in innere Energie (Verformungsenergie) umgewandelt.
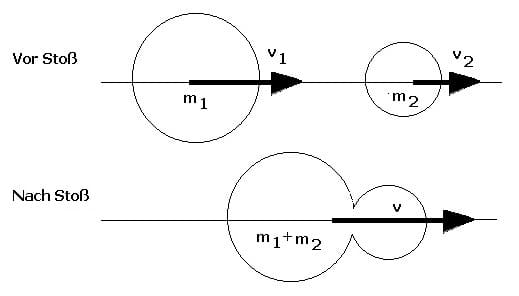
Aus

ergibt sich

Aus den Energien der Körper vor dem Stoß

und nach dem Stoß

kann die Verformungsarbeit errechnet werden:

Hierbei sind:
m1: Masse des Körpers 1 [kg]
m2: Masse des Körpers 2 [kg]
v1: Geschwindigkeit des Körpers 1 vor dem Stoß [m/s]
v2: Geschwindigkeit des Körpers 2 vor dem Stoß [m/s]
v: Gemeinsame Geschwindigkeit beider Körper nach dem Stoß [m/s]
E1: Summe der Bewegungsenergien beider Körper vor dem Stoß [J]
E2: Summe der Bewegungsenergien beider Körper nach dem Stoß [J]
W: Verformungsarbeit [J]
Programmbedienung - Beispiel
Legen Sie zunächst durch die Aktivierung des Kontrollschalters Elastischer Stoß bzw. Unelastischer Stoß fest, welchen dieser Zusammenhänge Sie analysieren möchten.
Durch die Positionierung der Rollbalken m1 und m2 legen Sie die Massen der beiden Wagen fest. Die Zuweisung der Geschwindigkeiten, die die Wagen vor dem Eintreten des Stoßes besitzen, bestimmen Sie durch die Positionierung der Rollbalken v1 und v2. Das Programm gibt hierauf die Werte für die Impulse p1 und p2 aus. Zudem zeigt es die Werte für die Energien E1' und E2' an. Es sind dies die Bewegungsenergien die die Wagen vor dem Stoß besitzen.
Bei Ausführung eines Klicks auf den Schalter Start führt das Programm die Simulation aus. Nach dem Eintreten des Stoßes werden die zudem Werte für die Geschwindigkeiten v1 und v2 ausgegeben, die die beiden Wagen hierauf besitzen.
Wird die Schaltfläche Urzustand bedient, so haben Sie die Möglichkeit, die Darstellung in den Anfangszustand zurückversetzen zu lassen. Beim unelastischen Stoß können Sie durch die Aktivierung des Kontrollkästchens Dauer-Simu festlegen, ob die Animation stetig wiederholt werden soll.
III - Teilelastischer Stoß
Teilelastischer Stoß:
Der elastische sowie der unelastische Stoß sind Idealfälle, welche in der Realität nicht auftreten. Vielmehr wird beim elastischen Stoß ein Teil der Verformungsarbeit wieder in kinetische Energie zurückverwandelt bzw. durch Reibung in andere Energieformen umgewandelt. Es handelt sich hierbei um einen teilelastischen Stoß. Somit tritt ein Energieverlust auf, welcher wie folgt näherungsweise ermittelt werden kann.
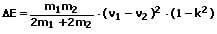
Aufrund des hierbei auftretenden Energieverlusts sind die Geschwindigkeiten der beiden Körper nach erfolgtem teilelastischen Stoß
geringer als nach einem elastischen Stoß. Sie können mit den nachfolgend aufgeführten Formeln berechnet werden.
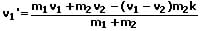
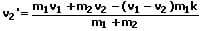
m1: Masse des Körpers 1 [kg]
m2: Masse des Körpers 2 [kg]
v1: Geschwindigkeit des Körpers 1 vor dem Stoß [m/s]
v2: Geschwindigkeit des Körpers 2 vor dem Stoß [m/s]
v1': Geschwindigkeit des Körpers 1 nach dem Stoß [m/s]
v2': Geschwindigkeit des Körpers 2 nach dem Stoß [m/s]
k: StoßzahlIV - Nicht zentraler Stoß - Schiefer Stoß
Nicht zentraler Stoß - Schiefer Stoß:
Beim geraden Stoß befinden sich die Bahnen, auf denen sich die Körper aufeinander zu bewegen, auf einer Linie. Diese Linie verläuft durch den Schwerpunkt der beteiligten Körper. Dies trifft beim schiefen Stoß (nicht zentralen Stoß bzw. dezentralen Stoß) nicht zu. Nachfolgend gezeigt sind die Abbildungen zweier unterschiedlicher schiefer Stöße.
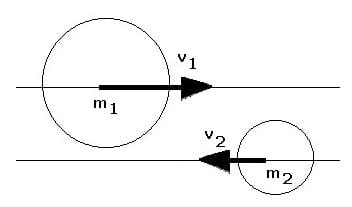
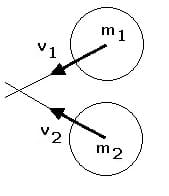
Die Durchführung von Berechnungen und die Ausgabe grafischer Darstellungen zu schiefen Stößen sind in diesem Unterprogramm nicht möglich.
Als Rückstoß wird die Gegenreaktion bezeichnet, die dann eintritt, wenn die Beschleunigung einer Masse erfolgt. Seine Richtung ist der Richtung der Beschleunigung entgegengesetzt. Er entspricht der Kraft, die auf einen Körper wirkt, wenn von diesem ausgehend eine Masse abgestoßen wird. Er ist eine Folge der Impulserhaltung und wird unter anderem zum Antrieb von Raketen genutzt. Es kann sich beispielsweise um einen Vorgang handeln, bei dem aufgrund einer chemischen Reaktion die Umwandlung von innerer Energie in kinetische Energie erfolgt. Für den Rückstoß gilt:
(m1 + m2)·v = m1·v' + m2·v'
m1: Masse des Körpers 1 [kg]
m2: Masse des Körpers 2 [kg]
v: Gemeinsame Geschwindigkeit beider Körper vor dem Rückstoß [m/s]
v1: Geschwindigkeit des Körpers 1 nach dem Rückstoß (Rückstoßgeschwindigkeit) [m/s]
v2: Geschwindigkeit des Körpers 2 nach dem Rückstoß (Rückstoßgeschwindigkeit) [m/s]
Geschwindigkeiten und Impulse, welche von links nach rechts vorliegen bzw. erfolgen, erhalten positive Vorzeichen, entgegengesetzte Richtungen werden negativ gekennzeichnet.
Der Rückstoß wird bei Düsentriebwerken und Raketen zu deren Antrieb ausgenutzt. Sie werden durch den Rückstoß ausströmender Gase vorwärts bewegt. Zur Fortbewegung von Flugapparaten dieser Art werden die Prinzipien des Impulserhaltungssatzes genutzt. Die Anwendung dieser Gesetzmäßigkeit wird das Raketenprinzip bzw. Rückstoßprinzip genannt.
Die Stoßzahl beschreibt das Verhältnis der endgültigen zur anfänglichen Relativgeschwindigkeit zwischen zwei Objekten, nachdem sie kollidiert sind.
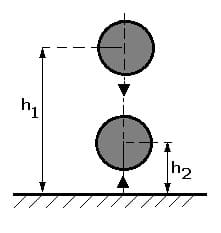
Sie wird wie folgt beschrieben:
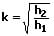
k: Stoßzahl
h1: Fallhöhe
h2: Höhe des Rückpralls
Ein Kraftstoß (eine Impulsänderung) kennzeichnet die Einwirkungsdauer (das Zeitintervall) einer Kraft auf einen Körper der Masse m. Ein Impuls hingegen beschreibt den Bewegungszustand eines Körpers unter Berücksichtigung seiner Masse. Er ist eine vektorielle Größe. Seine Richtung entspricht der der einwirkenden Kraft.
1. Konstante Kraft
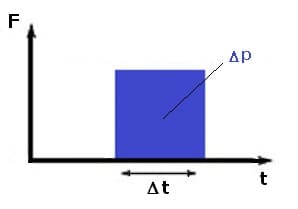
Ist die Kraft F innerhalb des Zeitintervalls Δt = t2-t1 konstant, so kann der Kraftstoß wie folgt berechnet werden:
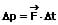
2. Nicht konstante Kraft
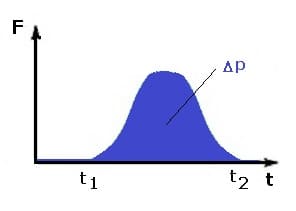
Ist die Kraft F innerhalb des Zeitintervalls Δt = t2-t1 nicht konstant, so gilt:
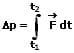

Impulssatz - Zusätzliche Abbildung 1

Impulssatz - Zusätzliche Abbildung 2

Impulssatz - Zusätzliche Abbildung 3
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Impulserhaltungssatz sowie unter Wikipedia - Stoß zu finden.
4-Takt-Ottomotor - Gleichförmige und gleichförmig beschleunigte Bewegung - Bewegung und Geschwindigkeit - Geschwindigkeit und Beschleunigung - Wellen - Druck in Flüssigkeiten - Ideale Strömung - Kinetische und potentielle Energie - Brownsche Bewegung - Molekularbewegung - Harmonische Schwingungen - Kreisbahnbewegung - Auftrieb - Geneigte Ebene - Freier Fall - Waagerechter und schiefer Wurf - Pendel - Chaos-Doppelpendel - Gedämpfte mechanische Schwingung - Rolle und Flaschenzug - Balkenwaage - Hebelgesetz - Zweites Newtonsches Gesetz - Drittes Newtonsches Gesetz - Mechanische Arbeit - Hookesches Gesetz
Unterprogramm Impulssatz

PhysProf 1.1 - Unterprogramm RLC-Kreis

MathProf 5.0 - Unterprogramm Kurven in Parameterform

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
















