PhysProf - Gedämpfte Schwingung - Feder - Dämpfung - Abklingen

Fachthema: Gedämpfte mechanische Schwingung

PhysProf - Mechanik - Physik verstehen - Ein Programm zur Visualisierung physikalischer Sachverhalte aus dieser Naturwissenschaft mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich hierfür interessieren. Es beinhaltet Anwendungen zu Grundlagen der Physik wie auch zu komplexeren Fachthemen.

Online-Hilfe für das Modul
zur Veranschaulichung geltender Gesetzmäßigkeiten und vorliegender Sachverhalte, welche bei der Bewegung eines vertikal angeordneten Federpendels herrschen.

Dieses Unterprogramm ermöglicht die Durchführung der Steuerung entsprechender Abläufe zur Echtzeit und bietet die Möglichkeit, die Einflüsse relevanter Größen interaktiv zu untersuchen.

Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.

 

Themen und Stichworte zu diesem Modul: Federpendel - Feder - Einhüllende - Frequenz - Elongation - Diagramm - Dämpfung - Dämpfen - Hüllkurve - Dämpfungskoeffizient - Dämpfungskonstante - Dämpfungsfaktor - Exponentialfunktion - DGL - Kreisfrequenz - Abklingzeit - Beispiel - Gedämpfte harmonische Schwingung - Freie gedämpfte Schwingung - Gedämpfte Schwingung - Mechanische Schwingung - Mechanische Schwingungen - Mechanik - Mechanisch - Federschwinger - Herleitung - Beweis - Dämpfungsmaß - Dämpfungsgrad - Lehrsches Dämpfungsmaß - Formel - Amplitude - Masse - Geschwindigkeit - Kriechfall - Aperiodischer Grenzfall - Vorgang - Vorgänge - Graph - Simulation - Animation - Aufgaben - Versuch - Zeit - Gedämpfte Schwingung - Gedämpftes Federpendel - Amplitudenverhältnis - Dämpfungsverhältnis - Experiment - Mathematik - Periode - Simulation - Schwingungen - Schwingungsgleichung - Geschwindigkeit - Linear gedämpfte Schwingung - Bewegung - Periodendauer - Differentialgleichung - Schwingfall - Schwingung - Gedämpft - Ungedämpft - Ruhelage - Konstante - Periodendauer - Auslenkung - Berechnen - Formel - Auslenkung einer Feder - Masse - Schwingungsamplitude - Maximale Amplitude - Schwingungsdämpfung - Schwingungsdauer - Schwingungskurve - Schwingende Feder - Freie Schwingung - Freie Schwingungen - Eigenfrequenz - Weg - Zeit - Zeichnen - Physik - Physikalisch - Was - Wie - Weshalb - Was ist - Warum - Bedeutung - Was bedeutet - Erklärung - Grundlagen - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgabeng - Beschreibung - Funktion - Gleichung - Ablauf - Abläufe - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Aufgaben - Lösungen - Begriff - Begriffe - Verändern - Veränderung - Ändern - Änderung - Einführung - Untersuchen -  Schwingungssimulation - Logarithmisches Dekrement - Rechner - Bild - Grafik - Grafische Darstellung

    

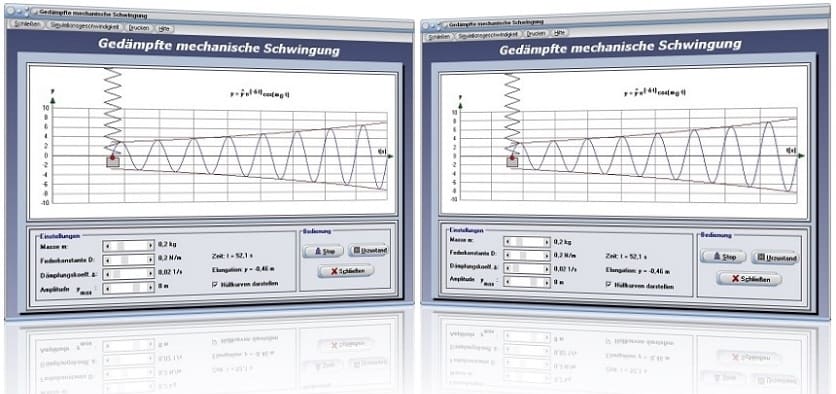
Modul Gedämpfte mechanische Schwingung

---

 
Mit Hilfe des Unterprogamms [Mechanik I] - [Gedämpfte mechanische Schwingung] können Zusammenhänge, welche bei der Bewegung eines vertikal angeordneten Federpendels vorherrschen, untersucht werden.
 

Gedämpfte Schwingung - Abbildung 1
 

Gedämpfte Schwingung - Abbildung 2
 

Gedämpfte Schwingung - Grundlegendes

 
Gedämpfte harmonische Schwingung - Freie gedämpfte Schwingung:

Mit dem Begriff freie gedämpfte Schwingung (oder gedämpfte harmonische Schwingung) wird eine Schwingung beschrieben, bei der sich ein Körper um eine Ruhelage bewegt. Als Dämpfung wird das Abnehmen (Dämpfen) einer Amplitude während des zeitlichen Verlaufs einer Schwingung bezeichnet. Sie resultiert aus der Umwandlung der Schwingungsenergie in andere Energieformen wie beispielsweise Wärmeenergie, welche unter anderem durch wirkende Reibungskräfte und Luftwiderstand verursacht wird. Als Auswirkung dieser Einflüsse zeigt sich die Abnahme der Auslenkung bis zum Erreichen der Ausgangsposition.
 

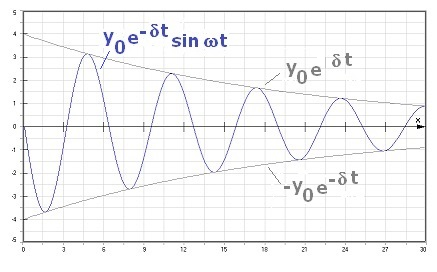
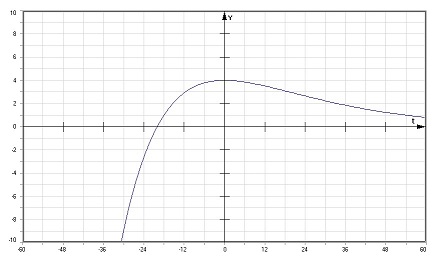
Abb.1: Gedämpfte Schwingung - Sinus - Exponentialfunktion


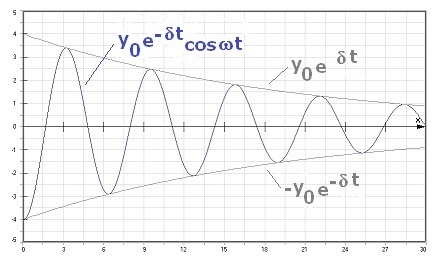
Abb.1: Gedämpfte Schwingung - Cosinus- Exponentialfunktion
 
Hinweis:
Die nachfolgend verwendeten Zeichen d und δ für den Abklingkoeffizienten eines schwingenden Systems besitzen die selbe Bedeutung.

Elongation (Auslenkung):

Die zeitabhängige Elongation (Auslenkung) der Amplitude einer derartigen Schwingung wird mit einer Exponentialfunktion beschrieben. Diese lautet:



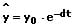
Der Wert einer zu einer bestimmten Zeit vorhandenen Elongation kann wie folgt beschrieben werden:


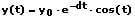
oder



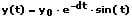
Hierbei wird die Stärke (Intensität) der Dämpfung mit der Dämpfungskonstante (dem Dämpfungskoeffizienten oder Dämpfungsfaktor) D beschrieben und die Abnahme der Elongation in Bezug zur Zeit wird durch den Faktor e^-dt bestimmt.

y(t): Elongation zur Zeit t
ŷ: Amplitude
ŷ₀: Anfangswert der Amplitude (bei t = 0)
d: Abklingkoeffizient
e: Eulersche Zahl = 2,71828 ...
t: Zeit [s]

Dämpfungsmaß (Dämpfungsgrad):

Das Dämpfungsmaß (oder Lehrsches Dämpfungsmaß) ist ein Maß für die Dämpfung eines schwingenden Systems. Für dieses gilt:



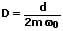
D: Dämpfungsmaß
d: Abklingkoeffizient
m: Masse [kg]
ω₀: Eigenkreisfrequenz der Schwingung ( = 2πf₀ = 2π/T₀) [1/s]

Eine Dämpfung bewirkt die zeitliche Veränderung der Schwingungsdauer und der Frequenz eines derartigen Systems.

Freie Schwingung:

Freie Schwingungen werden von einem schwingungsfähigen System ausgeführt, welches nach dem Auftreten einer Störung selbstständig in seinen Gleichgewichtszustand zurückkehrt.

Eigenfrequenz:

Als Eigenfrequenzen werden die Frequenzen eines derartigen Systems bezeichnet, mit denen dieses ohne den Einfluss externer Kräfte nach dessen einmalig erfolgtem Anstoß schwingen kann. Jede Schwingung eines Systems kann mittels seiner Eigenschwingungen interpretiert werden. Abhängig vom Abklingkoeffizienten δ erfolgt bei einer Dämpfung dessen, die zeitabhängige Änderung der Kreisfrequenz und der Frequenz sowie eine Vergrößerung der Schwingungsdauer des Systems.
 
Die Kreisfrequenz einer gedämpften Schwingung kann ermittelt werden mit:


 
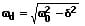
Die Schwingungsdauer einer gedämpften Schwingung ergibt sich mit:



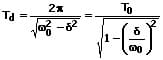
ω₀: Eigenkreisfrequenz der Schwingung [1/s]
ω_d: Kreisfrequenz der gedämpften Schwingung [1/s]
T_d: Schwingungsdauer der gedämpften Schwingung [s]
δ: Abklingkoeffizient 
 
Amplitudenverhältnis (Dämpfungsverhältnis):


 
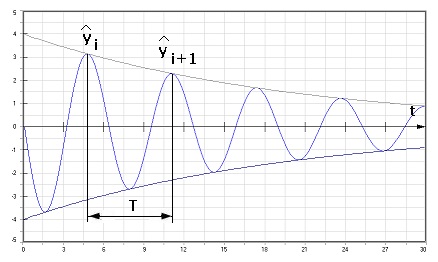
Als Amplitudenverhältnis (Dämpfungsverhältnis) wird der Quotient bezeichnet, der aus den Amplituden zweier aufeinanderfolgender Amplituden gebildet wird. Für die n-te Amplitude gilt:

q_n = ŷ_i / ŷ_i+1

Für den zeitlichen Abstand zweier aufeinanderfolgenden Amplituden mit einer Schwingungsdauer von T_d gilt:



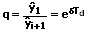
bzw.



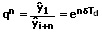
Als logarithmisches Dekrement Δ wird der Koeffizient δT_d bezeichnet. Für ihn gilt:



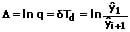
q,q_n: Amplitudenverhältnis
ŷ₀: Anfangswert der Amplitude (bei t = 0)
ŷ_i: Amplitude
e: Eulersche Zahl = 2,71828 ...
δ: Abklingkoeffizient
T_d: Schwingungsdauer der gedämpften Schwingung [s]
Δ: Logarithmisches Dekrement
 
Die Amplituden einer freien gedämpften Schwingung klingen exponentiell ab. Als Abklingzeit τ wird die Zeitspanne bezeichnet, in der ein Rückgang auf den e-ten Teil des Anfangswertes stattfindet.



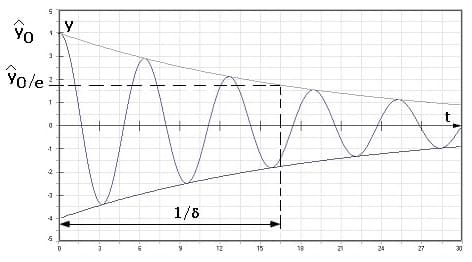
Die Abklingzeit einer mechanischen harmonischen Schwingung kann wie folgt berechnet werden:

τ = 1/δ

τ: Abklingzeit [s]
δ: Abklingkoeffizient [1/s]
   

Als Einhüllende (Hüllkurve oder Enveloppe) wird die Kurve eine mathematischen Funktion bezeichnet, die ene Kurvenschar einhüllt.

Als Kriechfall wird der Zustand eines schwingungsfähigen Systems beschrieben, in dem die Dämpfung so stark ist, dass keine Auslenkungen mehr stattfinden können.

Der aperiodische Grenzfall beschreibt den Dämpfungszustand eines harmonischen Systems, bei dem seine Schwingung schnellstmöglich in seine Ruhelage zurückkehrt.
 

Gedämpftes Federpendel

 
Bei einem (vertikalen) Federpendel (Federschwinger) handelt es sich um einen einfachen mechanischen Oszillator, bei dem sich ein an einer elastischen Feder angebrachter Körper auf- und abbewegt (schwingt). Zur Ausführung von Federschwingungen wird der am Federpendel angebrachte Körper etwas aus seiner Gleichgewichtslage ausgelenkt und hierauf losgelassen.
 
Ein Körper mit der Masse m befindet sich am freien Ende einer Feder mit der Federkonstante D. Der Körper und die Feder können sich ausschließlich in vertikaler Richtung bewegen. Das gesamte System befindet sich in einem viskosen Medium z.B. Wasser. Auf den Körper (und die Feder) wirken Reibungskräfte. Eine solche Anordnung wird als gedämpftes Federpendel bezeichnet.

Lenkt man den Körper in vertikaler Richtung aus der Ruhelage aus, hält ihn dort fest und lässt ihn daraufhin wieder los, so führt er eine periodische Bewegung aus.

Aufgrund dieser Annahmen wirken auf den Körper zu jedem Zeitpunkt der Bewegung zwei Kräfte. Es sind dies:

- die rücktreibende Kraft der Feder
- die Reibungskraft zwischen dem Medium und dem Körper

 

Aus diesen Zusammenhängen kann die nachfolgend gezeigte homogene Differentialgleichung 2. Ordnung (Schwingungsgleichung) zur Beschreibung der Elongation hergeleitet werden. Diese lautet:
 

 

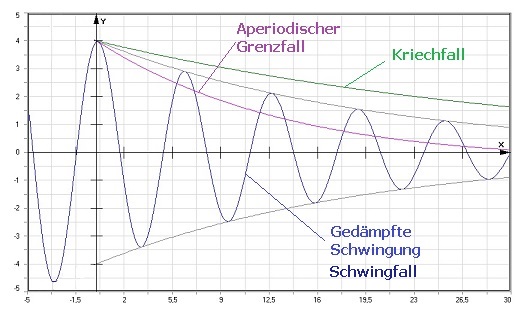
Die Lösung dieser Differentialgleichung führt zu folgenden Fällen:

1. Fall (schwache Dämpfung, Schwingfall): D/m > δ²

2. Fall (starke Dämpfung, aperiodischer Grenzfall): D/m > δ²

3. Fall (starke Dämpfung, Kriechfall): D/m < δ²
 
mit
 

 

und
 

 

Lösung der DGL im 1. Fall (schwache Dämpfung, Schwingfall) D/m > δ²:
 

 

Lösung der DGL im 2. Fall (starke Dämpfung, aperiodischer Grenzfall) D/m > δ²:
 

 

Lösung der DGL im 3. Fall (starke Dämpfung, Kriechfall) D/m < δ²:
 

 

mit

 

ŷ: Anfangswert der Amplitudenhüllkurve [m]

y: Elongation (Auslenkung zur Zeit t) [m]

t: Zeit [s]

ω₀: Kreisfrequenz der ungedämpften Schwingung [1/s]

δ: Dämpfungskoeffizient [1/s]

k: Reibungskonstante [kg/s]
e: Eulersche Zahl = 2,71828 ...

D: Federkonstante [N/m]

m: Masse des Körpers [kg]


Kriechfall - Aperiodischer Grenzfall:

Allgemein gelten für den Kriechfall sowie den aperiodischen Grenzfall die nachfolgend aufgeführten Zusammenhänge.

1. Kriechfall:

Liegt ein Kriechfall vor, so gilt für die Elongation zur Zeit t bei den Anfangswerten y₀ = 0 und v₀ = v_max:




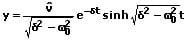
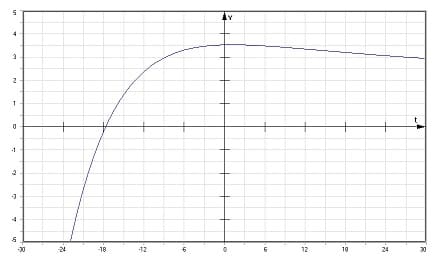
Bei den Anfangswerten y₀ = y_max und v₀ = 0 ergibt sich für den Kriechfall:





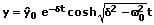
2. Aperiodischer Grenzfall:

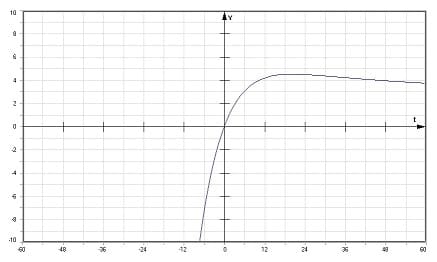
Liegt ein aperiodischer Grenzfall vor, so gilt für die Elongation zur Zeit t bei den Anfangswerten y₀ = 0 und _v0 = v_max:





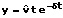
Bei den Anfangswerten y₀ = y_max und v₀ = 0 ergibt sich für den aperiodischen Grenzfall:





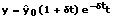
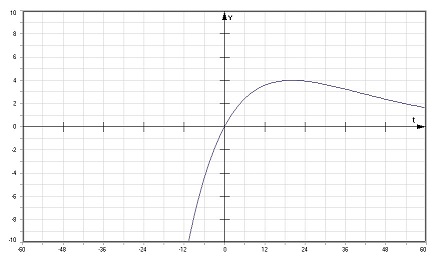
y: Elongation zur Zeit t
v_max: Maximalgeschwindigkeit bei y = 0
ŷ: Maximale Auslenkung bei v = 0
δ: Abklingkoeffizient
ω₀: Eigenkreisfrequenz der Schwingung [1/s]
e: Eulersche Zahl = 2,71828 ...
t: Zeit [s]

 

Programmbedienung

 
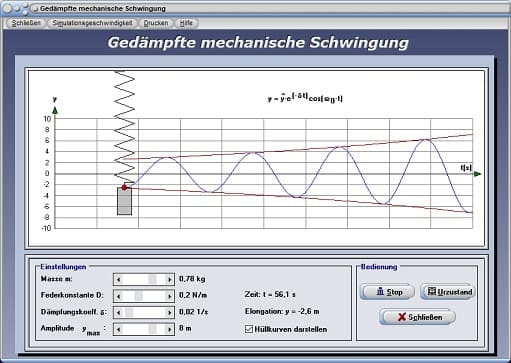
Dieses Unterprogramm simuliert eine gedämpfte mechanische Schwingung anhand des Beispiels einer an eine Feder angehängten Masse. Wird die Feder nach zuvor beschriebener Methode gedehnt und losgelassen, so entsteht eine Schwingung, deren Elongation im Laufe der Zeit t durch oben aufgeführte Einflüsse abnimmt.

Um eine derartig ablaufende Animation ausführen zu lassen, legen Sie durch die Benutzung der Rollbalken die Werte für die Parameter Masse m, Federkonstante D, Dämpfungskoeffizient δ und den Amplitudenwert y_max fest. Eine Aktivierung des Kontrollkästchens Hüllkurven veranlasst das Programm dazu, die Hüllkurven der Amplituden darzustellen.

Starten können Sie den Vorgang, indem Sie den Schalter Start bedienen. Durch die Ausführung eines erneuten Klicks auf diese Schaltfläche, welche hierauf die Bezeichnung Stop besitzt, beenden Sie die ablaufende Simulation wieder. Ein Klick auf die Schaltfläche Urzustand versetzt die Darstellung wieder in ihren Anfangszustand.

Während der Simulation werden die momentane Elongation (Y-Wert), sowie die seit dem Start verstrichene Zeit t in s angezeigt. Besitzen die Amplitudenwerte der Schwingung einen Wert nahe 0, so wird die Animation automatisch beendet.
 

Gedämpfte Schwingung - Abbildung 3


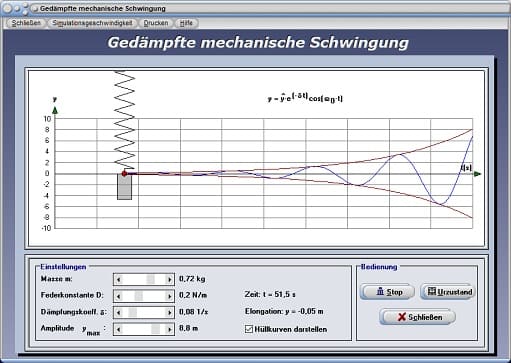
Gedämpfte Schwingung - Abbildung 4


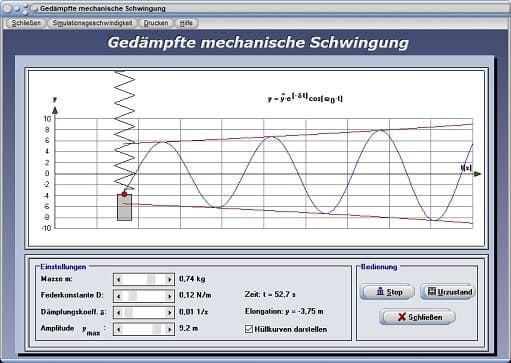
Gedämpfte Schwingung - Abbildung 5
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit. 
 

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.

 

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Linear gedämpfte Schwingung zu finden.
  

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

4-Takt-Ottomotor - Impulssatz - Gleichförmige und gleichförmig beschleunigte Bewegung - Bewegung und Geschwindigkeit - Geschwindigkeit und Beschleunigung - Wellen - Druck in Flüssigkeiten - Ideale Strömung - Kinetische und potentielle Energie - Brownsche Bewegung - Molekularbewegung - Harmonische Schwingungen - Kreisbahnbewegung - Auftrieb - Geneigte Ebene - Freier Fall - Waagerechter und schiefer Wurf - Pendel - Chaos-Doppelpendel - Rolle und Flaschenzug - Balkenwaage - Hebelgesetz - Zweites Newtonsches Gesetz - Drittes Newtonsches Gesetz - Mechanische Arbeit - Hookesches Gesetz
 

 

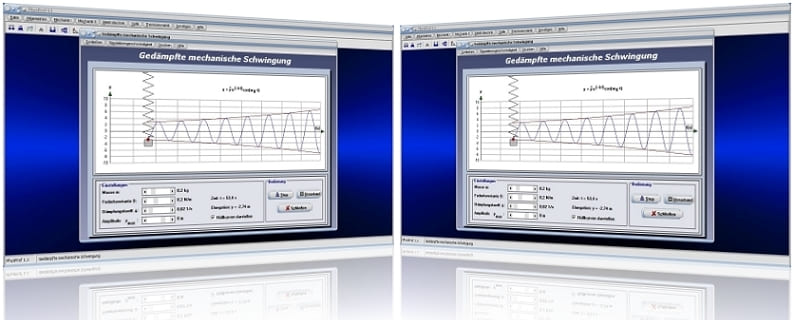
Unterprogramm Gedämpfte mechanische Schwingung
 

 

PhysProf 1.1 - Unterprogramm RLC-Kreis
 

MathProf 5.0 - Unterprogramm Kurven in Parameterform
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

 

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

 
 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---