PhysProf - Druck in Flüssigkeiten - Kraft - Fläche - Flüssigkeit
Fachthemen: Druck - Flüssigkeiten
PhysProf - Mechanik - Ein Programm zur Visualisierung physikalischer Sachverhalte und naturwissenschaftlicher Grundlagen mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.
Online-Hilfe für das Modul
zur Untersuchung des Verhaltens des statischen Drucks in Flüssigkeiten.
Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden physikalischen Sachverhalte.
Es eignet sich auch als Begleitung zu Versuchen im Physikunterricht, unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.
Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.
Themen und Stichworte zu diesem Modul: |
 |  |
Druck in Flüssigkeiten
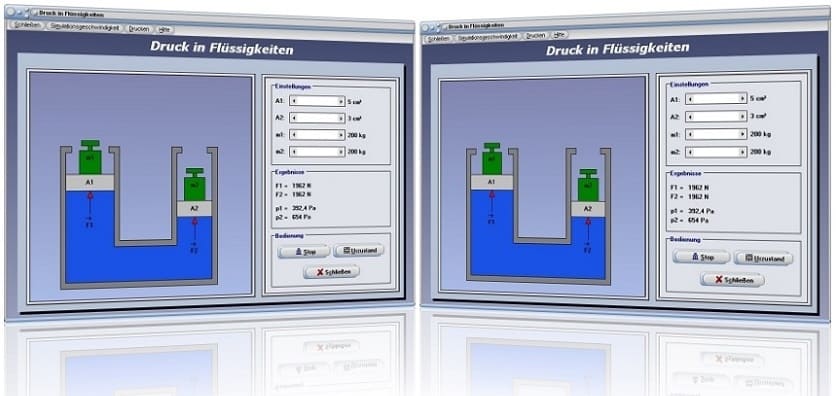
Modul Druck in Flüssigkeiten
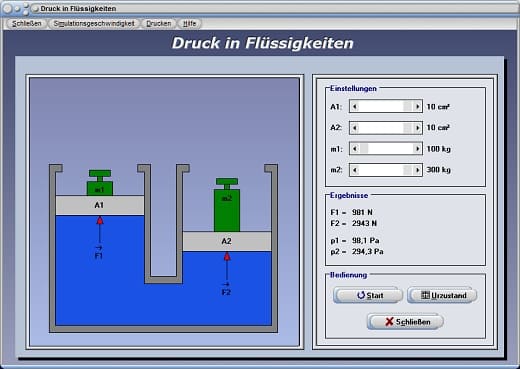
Mit Hilfe des Programmteils [Mechanik I] - [Druck in Flüssigkeiten] kann das Verhalten des statischen Drucks in Flüssigkeiten untersucht werden.
Druck in Flüssigkeiten - Abbildung 1
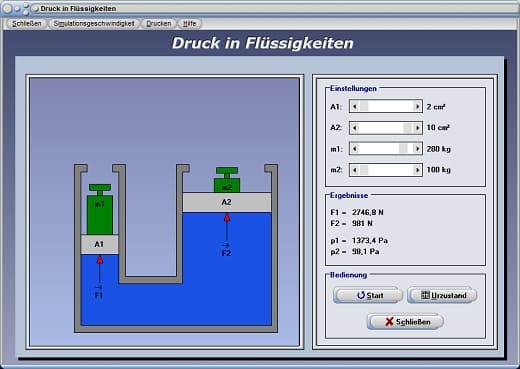
Druck in Flüssigkeiten - Abbildung 2
Physikalische Gesetze beschreiben Zustände sowie die Änderungen physikalischer Systeme mit Hilfe erfassbarer Daten in Form definierter physikalischer Größen. Der Auflagedruck erteilt Auskunft darüber, mit welcher Kraft ein Körper senkrecht auf ein Flächenareal von 1 Quadratmeter wirkt. Als hydraulischer Druck wird die physikalische Größe bezeichnet, die mittels eines Fluids auf die inneren Begrenzungsflächen eines geschlossenen hydraulischen Systems übertragen wird.
Pascalsches Gesetz:
Das Pascalsche Gesetz besagt unter anderem, dass der Druck einer Flüssigkeit konstant ist. Der Druck in ruhenden Flüssigkeiten (z.B. Wasser) breitet sich in allen Richtungen gleichmäßig aus. Die vom Druck erzeugte Kraft (oder die druckerzeugende Kraft bzw. Druckkraft) steht stets senkrecht auf den Grenzflächen der Flüssigkeit.
Die Kräfte verhalten sich wie die Flächen auf die sie wirken:
bzw.
Hieraus kann gefolgert werden:
Hierbei sind:
p,p1,p2: Drücke [Pa]
F1,F2: Kräfte [N]
A1,A2: Flächen [m²]
d1,d2: Durchmesser [m]
Hinweis:
1 bar entspricht 100 000 Pascal.
Das Verhältnis A1/A2 der beiden Flächen A1 und A2 wird als Flächenverhältnis bezeichnet.
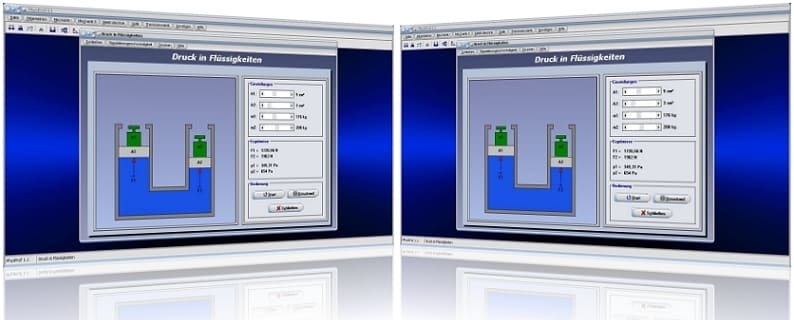
Die oben beschriebenen Sachverhalte liegen ebenfalls vor, wenn das System, wie nachfolgend gezeigt, angeordnet ist. Auch hier gilt: Die beiden Kräfte F1 und F2 verhalten sich wie die Quadrate der Kolbendurchmesser (bzw. wie die zugehörigen Flächen).
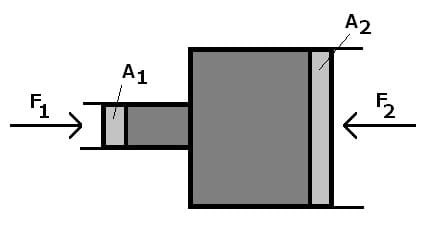
Als hydraulische Systeme oder Hydraulik werden Vorrichtungen (kraftumformende Einrichtungen) bezeichnet, die zur Übertragung von Kräften mittels Flüssigkeiten eingesetzt werden. In einem hydraulischen System (Hydrauliksystem) breitet sich der Druck p in alle Richtungen in gleicher Form aus.
Die Volumenverdrängung (das verdrängte Volumen) ergibt sich wie folgt:
Vv = A1 ⋅ s1 = A2 ⋅ s2
Gemäß der wirkenden Kräfte kann die hierbei verrichtete Arbeit berechnet werden. Es gilt:
W = F1 ⋅ s1 = F2 ⋅ s2
Vv: verdrängtes Volumen [m³]
A1,A2: Flächen [m²]
F1,F2: Kräfte [N]
s1,s2: Verschiebeweg [m]
W: verrichtete Arbeit [Nm]
Anwendung findet die oben beschriebene Gesetzmäßigkeit (diese Druckübersetzung und Kraftübersetzung) bei hydraulischen Hebeeinrichtungen wie z.B. Wagenheber, Hebebühnen oder anderen Druckübersetzern. Hydraulische Pressen setzen sich aus zwei Zylindern zusammen, die über unterschiedliche Durchmesser verfügen. Sie besitzen einen Kolben über den diese miteinander verbunden sind (siehe obige Abb.). Bei einer hydraulischen Presse wirkt auf die beiden Kolben derselbe Druck auf die verschieden großen Flächen des Kolbens (Kolbendruck), jedoch übt er auf diese unterschiedliche Kräfte aus.
Programmbedienung - Beispiel
Durch die Vorgabe verschiedener Ausgangswerte für Flächen und Massen, welche Sie durch die Positionierung der dafür vorgesehenen Rollbalken A1, A2, m1 und m2 festlegen, können Sie sich das Verhalten dieses Prinzips verdeutlichen.
Eine Simulation zur Analyse der Sachverhalte können Sie durchführen lassen, indem Sie die Schaltfläche Start bedienen. In den Anfangszustand zurückversetzen können Sie die Darstellung wieder durch die Bedienung der Schaltfläche Urzustand.
Aufgrund ihrer eigenen Gewichtskraft erfährt eine Flüssigkeit (z.B. Wasser) einen Schweredruck. Dieser beträgt je Meter Wasserhöhe ca. 104 Pa. Bei Schweredruck handelt sich um den Druck (Gewichtsdruck), den ein Körper nur auf Grund der Gewichtskraft der sich über ihm befindenden Flüssigkeit, oder des sich über ihm befindenen Gases erfährt. Als Wasserdruck wird der hydrostatische Druck des Wassers bezeichnet, der mit zunehmender Wassertiefe zunimmt.
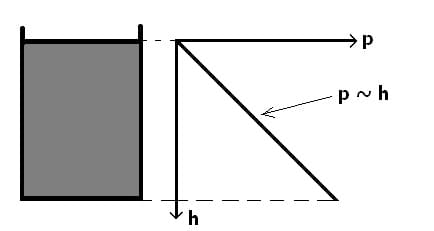
Es gilt:
p = G/A
G: Gewichtskraft der Flüssigkeit [N]
A: Fläche [m²]
oder:
p = ρgh
p: Schweredruck bei h [Pa]
h: Höhe der Flüssigkeitssäule [m]
ρ: Dichte der Flüssigkeit [kg/m³]
g: Fallbeschleunigung = 9,81 m/s²
Hydrostatisches Paradoxon:
Das hydrostatische Paradoxon besagt, dass der Bodendruck in einem mit ruhender Flüssigkeit befüllten Gefäß lediglich von der Flüssigkeitshöhe h, jedoch nicht von der Form des Gefäßes abhängt. Durch das Gewicht der Flüssigkeit wird an einem Punkt innerhalb dessen ein hydrostatischer Druck p gemäß
p(h) = ρ⋅g⋅h
erzeugt.
p: Schweredruck (hydrostatischer Druck) bei h [Pa]
h: Höhe des Flüssigkeitsspiegels [m]
ρ: Dichte der Flüssigkeit [kg/m³]
g: Fallbeschleunigung = 9,81 m/s²
Der hydrostatische Druck ist lediglich von der Tiefe unterhalb der Flüssigkeitsoberfläche (der Höhe des Flüssigkeitsspiegels) abhängig. Die in einem Gefäß enthaltene Flüssigkeitsmenge (und somit deren Masse) ist hierbei nicht von Bedeutung und somit besteht gemäß des oben gezeigten Sachverhalts in diesem Fall keine Abhängigkeit des Drucks von der Füllmenge des Gefäßes.
Umrechnung:
Die nachfolgend dargestellte Tabelle zeigt die Umrechnung einiger relevanter Einheiten des Drucks.
| 1 at = 735,6 Torr | = 98,0665 kPa |
| 1 mWS = 0,1 at | = 9,80665 kPa |
| 1 bar = 750 Torr | = 105 Pa |
| 1 atm = 760 Torr | = 1,01325⋅105 Pa |
| 1 Torr | = 133,3224 Pa |
| 1 mm HG | = 133,3224 Pa |
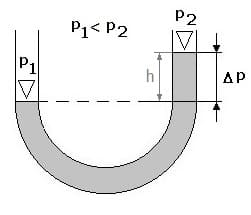
U-Rohr - Druckmessung - Druckdifferenz
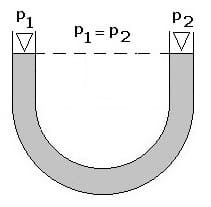
U-Rohr - Druckmessung - Gleicher Druck
Druckmessung - Druckmessgerät:
Zur Messung von Druckdifferenzen kann ein U-Rohr eingesetzt werden. Es handelt sich hierbei um ein Druckmessgerät, welches eine Flüssigkeit enthält. Die Verschiebung der Höhe ihrer Flüssigkeitssäule erteilt Auskunft über eine zwischen zwei Punkten existente Druckdifferenz. Herrscht auf einer Seite ein höherer Druck, so erhöht sich der Flüssigkeitsspiegel dieses Rohrs auf der Seite, auf welcher ein geringerer Druck vorhanden ist. Die entsprechende Druckdifferenz wird mit einem U-Rohr-Manometer gemessen. Es gilt:
Δp = p2 - p1 = ρf ⋅ g ⋅ h
Δp: Druckdifferenz [Pa]
ρf: Dichte der Flüssigkeit [kg/m³]
g: Fallbeschleunigung = 9,81 m/s
h: Höhe der Auslenkung des Manometers [m]
p1, p2: Drücke an den Enden des Manometers [Pa]
Druck in Flüssigkeiten - Abbildung 3
Druck in Flüssigkeiten - Abbildung 4
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Druck zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
4-Takt-Ottomotor - Impulssatz - Gleichförmige und gleichförmig beschleunigte Bewegung - Bewegung und Geschwindigkeit - Geschwindigkeit und Beschleunigung - Wellen - Ideale Strömung - Kinetische und potentielle Energie - Brownsche Bewegung - Molekularbewegung - Harmonische Schwingungen - Kreisbahnbewegung - Auftrieb - Geneigte Ebene - Freier Fall - Waagerechter und schiefer Wurf - Pendel - Chaos-Doppelpendel - Gedämpfte mechanische Schwingung - Rolle und Flaschenzug - Balkenwaage - Hebelgesetz - Zweites Newtonsches Gesetz - Drittes Newtonsches Gesetz - Mechanische Arbeit - Hookesches Gesetz
Unterprogramm Druck in Flüssigkeiten
PhysProf 1.1 - Unterprogramm RLC-Kreis
MathProf 5.0 - Unterprogramm Kurven in Parameterform
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Physik interaktiv
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
Eine Übersicht aller in MathProf 5.0 zur Verfügung stehender Programmteile finden Sie im MathProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
