PhysProf - Carnotscher Kreisprozess - Entropie - Wärmekraft

Fachthemen: Carnotscher Kreisprozess - Entropie - Wärmekraft

PhysProf - Thermodynamische Prozesse - Eine Anwendung zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren.

Zur effektiven Nutzung dessen wird ein bereits erlangtes Grundwissen zum entsprechenden Themengebiet vorausgesetzt.

Online-Hilfe für das Modul
zur grafischen Darstellung und Simulation der Vorgänge und Zusammenhänge beim Carnotschen Kreisprozesses.

Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden physikalischen Sachverhalte.

Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.

     

Themen und Stichworte zu diesem Modul: Carnot-Prozess - Carnot-Maschine - Kreisprozess - Thermodynamische Prozesse - Zustandsänderungen - Entropie - Entropieänderung - Entropiedifferenz - System - Temperatur - Volumen - Druck - Gas - Expansion - Kompression - Isotherme Expansion - Adiabatische Expansion - Isotherme Kompression - Adiabatische Kompression - Gase - Idealer Kreisprozess - Thermodynamischer Kreisprozess - Arbeit - Nutzarbeit - Zustandsgrößen - Thermischer Wirkungsgrad - Carnot - Carnot Prozess - Kreisprozesse - Carnot-Wirkungsgrad - Zustände - Wirkungsgrad - Herleitung - Beweis - Wärme - Wärmeenergie - Wärmeaustausch - Wärmeübertragung - Wärmemenge - Reversibel - Irreversibel - Reversibler Prozess - Irreversibler Prozess - Reversible Prozesse - Irreversible Prozesse - Spezifische Entropie - Temperatur-Entropie-Diagramm - Ts-Diagramm - Begriff - Begriffe - Gesetzmäßigkeiten - Wärmekraftmaschine - Wärmekraftmaschinen - Verändern - Veränderung - Ändern - Änderung - Innere Energie - Präsentation - Berechnen - Einführung - Grundlagen - Formeln - Vorgang - Vorgänge - Was - Wie - Weshalb - Was ist - Warum - Bedeutung - Was bedeutet - Erklärung - Einfach erklärt - Beschreibung - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Aufgaben - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Animation - Rechner - Diagramm - Bild - Grafik - Simulation - Berechnung - Darstellen - pV-Diagramm - Grafische Darstellung

   

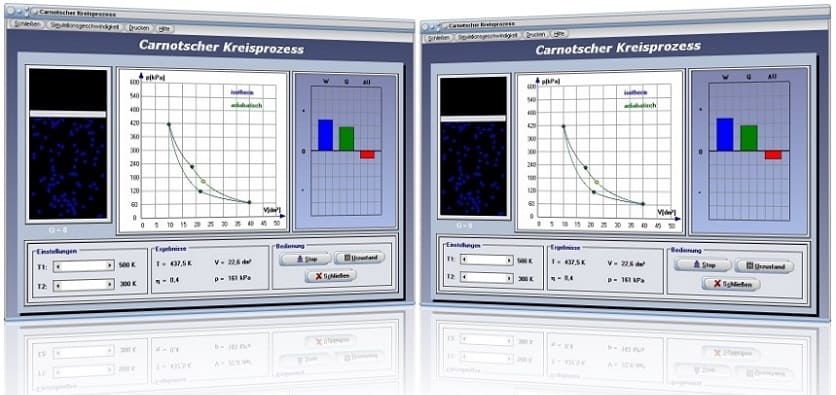
Modul Carnotscher Kreisprozess

---

Das Unterprogramm [Thermodynamik] - [Carnotscher Kreisprozess] ist dienlich, um sich die Zustände welche beim Durchlauf eines Carnotschen Kreisprozesses vorherrschen, verdeutlichen zu können.
 

Carnotscher Kreisprozess - Abbildung 1


Carnotscher Kreisprozess - Abbildung 2
 

Als Kreisprozess (thermodynamischer Kreisprozess) wird eine Ablauffolge bezeichnet, bei der nach dem Ablauf einer Reihe von Zustandsänderungen der urspüglich zugrundeliegende Ausgangszustand wieder erreicht wird.
 
Zustandsgrößen: Bei einer Zustandsgröße handelt es sich um eine makroskopische physikalische Größe (den Parameter einer Zustandsgleichung), die den momentanen Zustand eines physikalischen Systems beschreibt. Sie ist lediglich vom momentanen Zustand des Systems abhängig, nicht jedoch vom Weg, über welchen dieser erreicht wurde.
 
Als Carnotscher Kreisprozess wird ein wichtiger Grundprozess der Thermodynamik bezeichnet. Er wird als idealer theoretischer Vergleichsprozess verwendet, um viele reale Prozesse zu untersuchen. Es ist ein Wärmekraftprozess, welcher auch als idealer Kreisprozess bezeichnet wird. Bei allen Wärmekraftmaschinen ist eine möglichst vollständige Verwandlung von Wärmeenergie in mechanische Energie erwünscht. Carnot fand heraus, dass es am günstigsten ist, wenn das Gas einen bestimmten Kreisprozess durchläuft.

Der Carnot-Wirkungsgrad ist der höchste, theoretisch mögliche Wirkungsgrad der bei einer Umwandlung von Wärmeenergie in mechanische oder elektrische Energie erreicht werden kann. Bei einem Carnot-Prozess handelt es sich um einen idealen Kreisprozess, der exakt diesen Wirkungsgrad besitzt.

Beim Carnotschen Kreisprozess finden vier aufeinander folgende Zustandsänderungen (thermodynamische Prozesse) statt. Dies sind:
 

1. Isotherme Expansion
2. Adiabatische Expansion
3. Isotherme Kompression
4. Adiabatische Kompression

 

Beschreibung der o.a. Zustandsänderungen:
 

1. Ein Gas wird mit einem Wärmereservoir in Kontakt gebracht, beide haben dieselbe Temperatur T₁. Das Gas expandiert und entzieht dem Wasserreservoir Wärme, in dem dieses das Gas auf konstanter Temperatur hält. Bei der Expansion leistet das Gas Arbeit.
    

2. Das Gas wird vom Wärmereservoir getrennt und expandiert weiter. Die Energie für die dabei geleistete Arbeit stammt aus dem Gas, welches sich daher abkühlt und danach die niedrigere Temperatur T₂ besitzt.
    

3. Das Gas wird mit einem zweiten (kälteren) Wärmereservoir der Temperatur T₂ in Kontakt gebracht und isotherm komprimiert. Dazu wird mechanische Arbeit benötigt und in Wärme umgesetzt, welche an das Reservoir abgegeben wird.
    

4. Das Gas wird vom zweiten Wärmereservoir getrennt und adiabatisch weiter komprimiert. Die hierbei am Gas verrichtete Arbeit erwärmt dieses wieder auf die Temperatur T₁. Nach dem vierten Schritt muss sich das Gas wieder im Ausgangszustand befinden, da nur dadurch ein Kreisprozess möglich ist, welcher periodisch fortgesetzt werden kann.

 
 
Die bei den ersten beiden Schritten gewonnene Arbeit ist größer als die bei den letzten beiden Schritten eingebrachte Arbeit, so dass sich insgesamt ein Arbeitsgewinn ergibt. Die Tatsache, dass man stets zwei Energiereservoirs benötigt, um eine Wärmekraftmaschine zu betreiben, ist eine wichtige Erkenntnis von Carnot.

Wird der Carnot-Prozess in umgekehrter Richtung durchlaufen, so entzieht er dem kälteren Reservoir Wärme und führt sie dem wärmeren Reservoir (zusammen mit der in Wärme umgesetzten Arbeitsenergie) zu. Eine solche Vorrichtung wird Wärmepumpe genannt. Wärmepumpen werden z.B. als Kühlaggregate oder zur energiesparenden Beheizung von Gebäuden verwendet.
 

Thermischer Wirkungsgrad: Der thermische Wirkungsgrad des Carnot-Prozesses (der Carnot-Wirkungsgrad) errechnet sich wie folgt:
 

T₁: Anfangstemperatur [K]
T₂: Endtemperatur [K]
η: thermischer Wirkungsgrad

 
Die bei einem Carnot-Prozess verrichtete Arbeit bildet sich aus der Summe der einzelnen bei den oben aufgeführten Zustandsänderungen verrichteten Arbeiten. Es gilt:

W_C = W_iso12 + W_ad23 + W_iso34 + W_ad41

Die Nutzarbeit des Carnot-Prozesses errechnet sich aus der Summe der zugeführten Arbeit bei Zustand 12 und der abgeführten Arbeit bei Zustand 34. Für sie gilt:

W_N = W_iso12 + W_iso34
 
 

Reversible Prozesse - Irreversible Prozesse:

Als reversibler Prozess wird ein thermodynamischer Prozess bezeichnet, der ohne erneute Energiezufuhr wieder umgekehrt ablaufen könnte. Alle anderen thermischen Vorgänge werden als irreversibel bezeichnet.

Jeder reversible Kreisprozess besitzt genau denselben Wirkungsgrad wie der Carnot-Prozess, wenn die mittleren thermodynamischen Temperaturen bei der Wärmezufuhr und bei der Wärmeabfuhr mit denen der Isothermen im Carnot-Prozess übereinstimmen.
 

Programmbedienung

 
Mit Hilfe des zur Verfügung stehenden Modells ist es möglich sich diesen reversiblen Kreisprozess in einem idealen Gas zu veranschaulichen. Hierbei werden zwei adiabatische sowie zwei isotherme Prozesse durchlaufen. Durch Bedienung der Schieberegler T1 und T2 können die Temperaturen der Reservoirs eingestellt werden. Am dargestellten Energiediagramm werden die Änderung der inneren Energie ΔU, die dem System zugeführte Wärmeenergie Q und die am System verrichtete Arbeit W ermittelt. Auch wird der Wirkungsgrad des Kreisprozesses ausgegeben. Starten können Sie die Simulation, indem Sie die Schaltfläche Start bedienen. Mit Hilfe des Schalters Urzustand versetzen Sie die Darstellung wieder in den Anfangszustand.
 

Entropie - Entropieänderung - Entropiedifferenz

Bei einem Carnotschen Kreisprozess sind die reversibel ausgetauschte Wärmemenge Q sowie die Temperatur T während des Austausches proportional. Der Quotient Q/T wird als reduzierte Wärmemenge bezeichnet. Bei jedem vonstatten gehenden Kreisprozess ist die Summe der reduzierten Wärmemengen gleich Null und bei jedem Zyklus eines reversiblen Kreisprozesses erreichen alle Zustandsgrößen ihren Anfangszustand. Ihre Änderung ist null, da diese Summe der reduzierten Wärmemengen gleich Null ist.

Die Zustandsgröße welche diese Zusammenhänge beschreibt, wird als Entropie S bezeichnet. Sie ist das Maß, welches die Umkehrbarkeit thermodynamischer Vorgänge widergibt, sowie ein Maß für die Verteilung von Energie und Materie.
 
Die Entropieänderung dS beschreibt die Entropie während eines umkehrbaren Prozesses. Sie ist bei einer Wärmezufuhr positiv, bei einer Wärmeabfuhr negativ. Ihre Definition lautet:


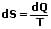
SI-Einheit der Entropie: [S] in J/K

Die in einem abgeschlossenen System vorhandene Entropie eines Gases kann durch darin ablaufende Vorgänge niemals abnehmen. Für dieses gilt

ΔS ≥ 0

Die Entropieänderung eines idealen Gases kann wie folgt berechnet werden:


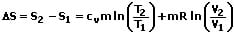
Für die Entropieänderung bei entsprechenden Zustandsänderungen gilt folgendes:

Isochore Zustandsänderung: ΔS = c_vm ln(T₂/T₁)
Isotherme Zustandsänderung: ΔS = mR ln(V₂/V₁)
Adiabatische Zustandsänderung: ΔS = 0

ΔS: Entropieänderung
m: Gasmasse [kg]
c_v: spez. Wärmekapazität des Gases [J/(kg·K)]
T₁: Anfangstemperatur des Gases [K]
T₂: Endtemperatur des Gases [K]
V₁: Anfangsvolumen des Gases [m³]
V₂: Endvolumen des Gases [m³]
R: Gaskonstante [J/(kg·K)]
 
Der Nullpunkt der Entropie wird in den meisten Fällen der Technik auf den Wert 273,15 K bzw 0°C gelegt. Jeder Stoff und jedes System verfügt über eine Entropie. Durch verschiedene Prozesse und somit der Verrichtung von Arbeit, verändert sich dessen Entropie. Diese Veränderung findet jedoch ausschließlich in eine Richtung statt. Die Entropie eines Stoffes kann stets nur gleich bleiben oder zunehmen. Sie kann jedoch niemals abnehmen!
 
Für zwei verschiedene Zustände folgt die Entropiedifferenz:


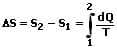
Diese ist bei einem reversiblen Kreisprozess gleich Null (ΔS = 0). Bei einem irreversiblen Prozess ist sie größer Null (ΔS > 0).

Der Entropiebegriff lässt sich außer auf den Carnotschen Kreisprozess auf alle thermodynamischen Prozesse anwenden.

Als spezifische Entropie wird die Entropie je Maßeinheit bezeichnet. Es gilt:

s = S/m

s: spezifische Entropie [J/kg]
S: Entropie [J/K]
m: Masse [kg]
 

Temperatur-Entropie-Diagramm

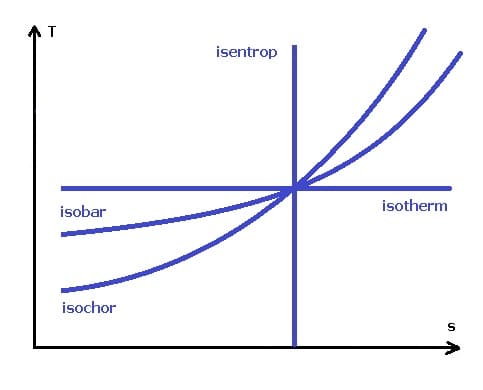
Abb. 1 - TS-Diagramm - Thermische Prozesse

Das Temperatur-Entropie-Diagramm (Ts-Diagramm) findet Anwendung, um Veränderungen der Temperatur und der spezifischen Entropie, die während eines thermodynamischen Prozesses oder Zyklus stattfinden, zu visualisieren. Bei reversiblen Kreisprozessen entspricht die Fläche unter der Ts-Kurve eines Wärmeprozesses der Wärmemenge, die während dessen auf das System übertragen wird.


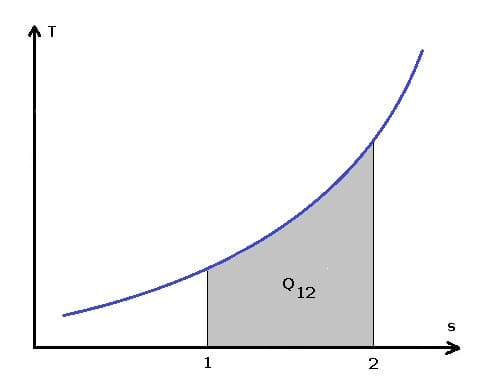
Abb. 2 - TS-Diagramm - Wärmemenge

Die zwischen zwei Zuständen 1 und 2 übertragene Wärmemenge kann wie folgt berechnet werden:


 

Wärmekraftmaschinen

 
Wärmekraftmaschinen sind Maschinen, die Wärme in mechanische Energie (Arbeit) umwandeln. Ihrem Medium wird bei hoher Temperatur Wärmeenergie zugeführt, welche teilweise in mechanische Energie umgewandelt wird. Der restliche Anteil wird wieder in Form von Wärmeenergie abgegeben. Beispiele für Maschinen dieser Art sind Dampfturbinen, Dampfmaschine sowie Verbrennungsmotoren.


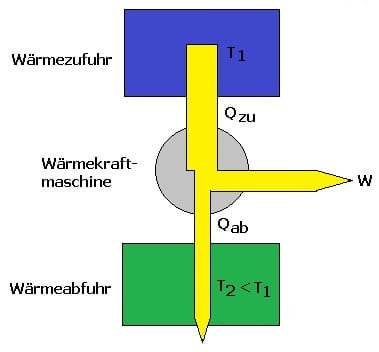
Wärmekraftmaschinen nutzen Kreisprozesse, bei denen Zustandsänderungen die Umwandlung von Wärme in mechanische Energie vollführen.

Maschinen dieser Art verwenden rechtslaufende Kreisprozesse. Dies bedeutet, dass bei solch einem Prozess die Kurve in einem p-V-Diagramm im Uhrzeigersinn durchlaufen (von oben nach rechts, von unten nach links) wird. Für deren thermischen Wirkungsgrad gilt oben gezeigte Formel (thermischer Wirkungsgrad eines Carnot-Prozesses).
  

 

Carnotscher Kreisprozess - Abbildung 3
 

Carnotscher Kreisprozess - Abbildung 4
 

Carnotscher Kreisprozess - Abbildung 5
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
 
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit. 
  

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.

 

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Carnot-Prozess zu finden.
 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

Isochore Zustandsänderung - Isobare Zustandsänderung - Isotherme Zustandsänderung - Adiabatische Zustandsänderung - Aggregatzustände - Mischungsregel - Reales Gas - Molekülgeschwindigkeit
 

 

Unterprogramm Carnotscher Kreisprozess
 

 

PhysProf 1.1 - Unterprogramm RLC-Kreis
 

MathProf 5.0 - Unterprogramm Kurven in Parameterform
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

    

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

 
 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---