PhysProf - Balkenwaage - Waage - Drehmoment - Gewicht
Fachthemen: Balkenwaage - Waage - Drehmoment
PhysProf - Mechanik - Ein Programm zur Visualisierung physikalischer Sachverhalte mittels Simulationen und 2D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure und alle die sich für Physik interessieren. Neben dem Einsatz zur Durchführung wissenschaftlicher Untersuchungen kann es als Lernsoftware für Schüler der Oberstufe eingesetzt werden.
Online-Hilfe für das Modul
zur Veranschaulichung des Wirkungsprinzips der Balkenwaage.
Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Untersuchung der entsprechenden physikalischen Sachverhalte und eignet sich zudem als ergänzendes Unterrichtsmaterial zum Physikunterricht.
Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.
Weitere relevante Seiten zu diesem Programm
Themen und Stichworte zu diesem Modul: |
 |  |
Balkenwaage - Waage
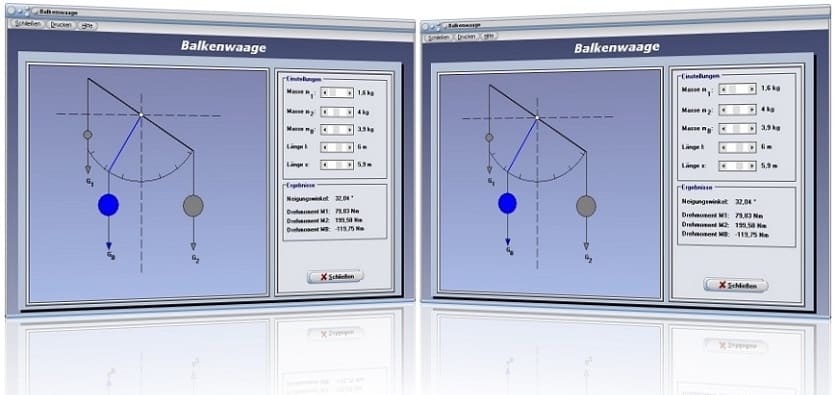
Modul Balkenwaage
Das Unterprogramm [Mechanik II] - [Balkenwaage] ermöglicht es, das Wirkungsprinzip der Balkenwaage zu analysieren.
Balkenwaage - Abbildung 1
Balkenwaage - Abbildung 2
Waagen sind Messgeräte die zur Bestimmung der Masse bzw. zur Feststellung des Gewichts (zur Gewichtsbestimmung) von Körpern eingesetzt werden. Eine Balkenwaage (Hebelwaage) ist eine Wiegevorrichtung, welche aus einem horizontal angeordneten Balken besteht, der beweglich an einer waagrechten Achse gelagert ist. Der Schwerpunkt des Gestänges der Balkenwaage liegt unterhalb des Drehpunkts.
Drehmoment
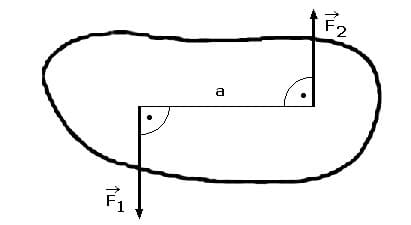
Unter einem Drehmoment (Kraftmoment) wird das Produkt aus einer Kraft und dem senkrechten Abstand ihrer Wirkungslinie vom Drehpunkt verstanden. Wirken die Drehmomente in einer Ebene, so werden linksdrehende Momente als positiv bezeichnet, wirken sie hingegen rechtsdrehend, so werden sie als negativ angegeben. Die Einheit eines Drehmoments ist das Newtonmeter [Nm].
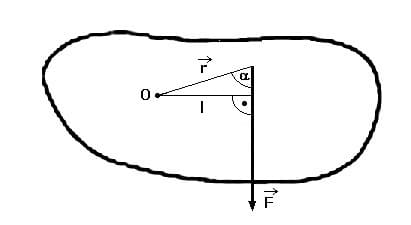
Es gilt:
M = F·l = F·r·sin(α)
M: Drehmoment [Nm]
F: Wirkende Kraft [N]
l: Vertikale Distanz zwischen Drehpunkt und Angriffspunkt [m]
r: Distanz zwischen Drehpunkt und Angriffspunkt [m]
α: Winkel zwischen F und r
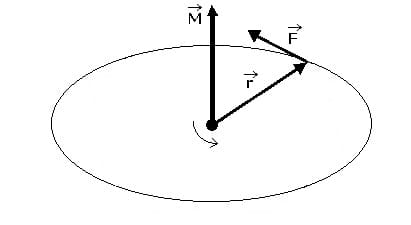
Räumlich betrachtet ist das Drehmoment M das Vektorprodukt der Vektors r und der Kraft F. Es gilt:
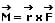
Gleichgewicht
Als Gewicht (Gewichtskraft) wird die durch die Wirkung einer Gravitation ausgeübte Kraft auf einen Körper bezeichnet. Sie berechnet sich aus der Masse m der Körpers sowie der Fallbeschleunigung mit F = m⋅g.
Gleichgewichtslage:
Hinsichtlich der Gleichgewichtslage von Körpern wird unterschieden zwischen:
- Stabile Lage (stabiles Gleichgewicht)
- Labile Lage (labiles Gleichgewicht)
- Indifferente Lage (indifferentes Gleichgewicht)
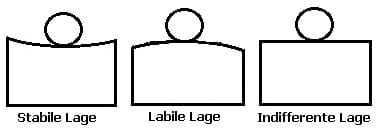
Bei einer stabilen Lage (stabiles Gleichgewicht) hebt sich der Schwerpunkt des Körpers. In einer labilen Lage (labiles Gleichgewicht) senkt er sich und bei einer indifferenten Lage (indifferentes Gleichgewicht) verharrt er in gleicher Höhe.
Statisches Gleichgewicht - Dynamisches Gleichgewicht (Fließgleichgewicht):
Gleichgewichte werden grundsätzlich in zwei Klassen unterteilt. Es sind dies:
- statisches Gleichgewicht
- dynamisches Gleichgewicht
Als statisches Gleichgewicht wird ein Gleichgewichtszustand bezeichnet, bei dem sich nichts ändert. Ein Körper (oder ein gekoppeltes System von Körpern) befindet sich im statischen Gleichgewicht, wenn sich alle von außen wirkenden Kräfte beziehungsweise Drehmomente gegenseitig aufheben.
Ein dynamisches Gleichgewicht (Fließgleichgewicht) befindet sich stets in Bewegung. Es tritt ein, wenn zwei oder mehrere Prozesse sich in ihrer Wirkung gegenseitig aufheben.
Kräftegleichgewicht - Momentengleichgewicht - Gleichgewichtsbedingungen:
Die auf einen starren Körper wirkenden Kräfte (Gewichtskräfte) können sowohl eine Translation wie auch eine Drehbewegung zur Folge haben. Um einen Körper im Gleichgewicht zu behalten, müssen die nachfolgend aufgeführten Bedingungen erfüllt sein:
Momentengleichgewicht: Die Summe aller wirkenden Drehmomente um jeden (einen) beliebigen Punkt muss gleich Null sein
Kräftegleichgewicht: Die Resultierende aller wirkenden Kräfte muss gleich null sein
Gegengewicht: Als Gegengewicht wird ein Körper mit einer bestimmten Masse bezeichnet, der zum Ausgleich einseitig wirkender Kräfte (Drehmomente) oder zum Ausgleich von Gewichtsverteilungen dient.
Balkenwaage
Nachfolgend aufgeführt erfolgt die Berechnung der bei einer Balkenwaage wirkenden Drehmomente.
Im vorliegenden Fall gelten, wie oben gezeigt, folgende Bedingungen:
Bedingung für das Momentengleichgewicht (Summe aller Drehmomente - vektoriell):
m,Δm,mB: Masse [kg]
l: Lastarm [m]
M1 (links), M2 (rechts), MB (Gestänge): Drehmomente [Nm]
xs: Horizontaler Abstand des Schwerpunkts vom Drehpunkt [m]
g: Fallbeschleunigung [m/s²]
s: Länge des Gestänges der Waage [m]
α: Neigungswinkel des Lastarms in °
Wird die Waage ungleich belastet, so verlagert sich der Schwerpunkt so lange bis das Drehmoment der Last und das Drehmoment des Schwerpunkts ausgeglichen wird. Die Bilanz der Drehmomente zeigt, von welchen Parametern die Empfindlichkeit der Waage abhängt.
Als Neigungswinkel wird derjenige Winkel angegeben, durch welchen die Neigung einer Gerade o. ä. bestimmt wird.
Programmbedienung
Durch die Bedienung der zur Verfügung stehenden Rollbalken Masse m1, Masse m2, Masse mB, Länge l und Länge s können Sie die beiden außen angehängten Massen m1 und m2, die in der Mitte angehängte Masse mB, die Länge des Waagebalkens l sowie die Länge s des grün markierten Balkens verändern.
Das Programm ermittelt bei jeder Zustandsänderung die aktuellen Werte für die wirksamen Drehmomente M1, M2 und MB und gibt den Neigungswinkel des horizontal angeordneten Balkens aus.
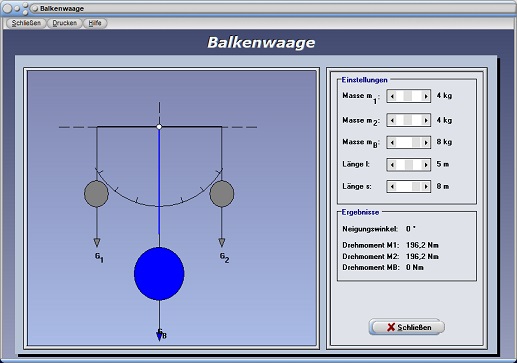
Balkenwaage - Abbildung 3
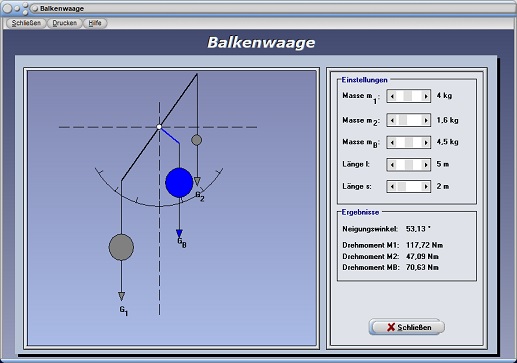
Balkenwaage - Abbildung 4
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Balkenwaage zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
4-Takt-Ottomotor - Impulssatz - Gleichförmige und gleichförmig beschleunigte Bewegung - Bewegung und Geschwindigkeit - Geschwindigkeit und Beschleunigung - Wellen - Druck in Flüssigkeiten - Ideale Strömung - Kinetische und potentielle Energie - Brownsche Bewegung - Molekularbewegung - Harmonische Schwingungen - Kreisbahnbewegung - Auftrieb - Geneigte Ebene - Freier Fall - Waagerechter und schiefer Wurf - Pendel - Chaos-Doppelpendel - Gedämpfte mechanische Schwingung - Rolle und Flaschenzug - Hebelgesetz - Zweites Newtonsches Gesetz - Drittes Newtonsches Gesetz - Mechanische Arbeit - Hookesches Gesetz
Unterprogramm Balkenwaage
PhysProf 1.1 - Unterprogramm RLC-Kreis
MathProf 5.0 - Unterprogramm Kurven in Parameterform
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Physik interaktiv
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
Eine Übersicht aller in MathProf 5.0 zur Verfügung stehender Programmteile finden Sie im MathProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
