PhysProf - Auftrieb - Auftriebskraft - Flüssigkeit - Dichte - Umrechnung
Fachthemen: Auftrieb - Dichte
PhysProf - Mechanik - Ein Programm zur Visualisierung physikalischer Sachverhalte und zur Ergründung physikalischer Gesetze mittels Simulationen und 2D-Animationen für das Berufskolleg, für die Oberstufe, für Abiturienten, für Studenten sowie für technische Berufe, Ingenieure und alle die sich für Physik interessieren. Zur effektiven Benutzung dessen wird ein bereits erlangtes Grundwissen zum entsprechenden Themengebiet vorausgesetzt.
Online-Hilfe für das Modul
zur Untersuchung der Gesetzmäßigkeiten und Kräfte, die beim Auftrieb in Flüssigkeiten vorherrschen.
Dieses Teilprogramm ermöglicht die Durchführung interaktiver Analysen zu diesem Fachthema sowie eine Veranschaulichung der entsprechenden physikalischen Sachverhalte und eignet sich auch als Begleitung zu Versuchen im Physikunterricht.
Es unterstützt dabei ein tiefergehendes Verständnis zu diesem Themengebiet zu erlangen und kann zum Lösen vieler diesbezüglich relevanter Aufgaben eingesetzt werden.
Weitere relevante Seiten zu diesem Programm
Themen und Stichworte zu diesem Modul:Auftrieb - Auftriebskraft - Auftrieb berechnen - Auftriebskraft berechnen - Hydrostatik - Gewichtskraft - Schwimmstabilität - Schwimmende Körper - Schwimmender Körper - Schwebender Körper - Volumen - Dichte - Wichte - Dichtetabelle - Schwerkraft - Bild - Definition - Fallbeschleunigung - Eintauchtiefe - Tiefgang - Experiment - Rechner - Auftrieb in Flüssigkeiten - Wasser - Auftrieb im Wasser - Tiefe - Druck - Steigen - Schwimmen - Schweben - Sinken - Schwimmkörper - Auftriebskörper - Tauchen - Simulation - Wirkung - Grundlagen - Kraft - Archimedes - Archimedisches Prinzip - Archimedisches Gesetz - Schwebezustand - Statischer Auftrieb - Hydrostatischer Auftrieb - Eis - Verdrängtes Volumen - Wasservolumen - Verändern - Veränderung - Ändern - Änderung - Berechnung - Berechnungsformel - Darstellung - Darstellen - Experiment - Physik - Physikalisch - Versuch - Herleitung - Beweis - Unterricht - Auftriebsberechnung - Masse - Flüssigkeit - Verdrängung - Verdrängungsvolumen - Bedeutung - Was bedeutet - Wie viel - Wieviel - Was - Wie - Weshalb - Was ist - Warum - Erklärung - Einfach erklärt - Beschreibung - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Aufgaben - Lösungen - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Einführung - Bodendruckkraft - Berechnen - Körper - Grafik - Gleichung - Abtrieb - Newton - Gewicht - Gas - Flüssigkeit - Physikalische Formel - Formel - Formelzeichen - Einheit - Physikalische Einheit - Erdbeschleunigung - Feste Stoffe - Dichte umrechnen - Dichteeinheiten - Dichteberechnung - Gase - Gasförmige Stoffe - Mittlere Dichte - Durchschnittliche Dichte - Normdichte - Dichte von Stoffen - Stoffdichte - Bestimmen - Bestimmung - Dichte bestimmen - Dichte messen - Dichtebestimmung - Dichtemessung - Hydrostatische Waage - Tabelle - Dichtemessgerät - Begriff - Begriffe - Einheit - Einheiten - Maßeinheit - Rho - g/cm3 - kg/m3 - g/m3 - g/dm3 - g/l - Liter - kg/l - Umrechnen - Umrechnung - Umrechnungstabelle - Umrechnungsfaktor |
Auftrieb - Archimedisches Prinzip - Dichte
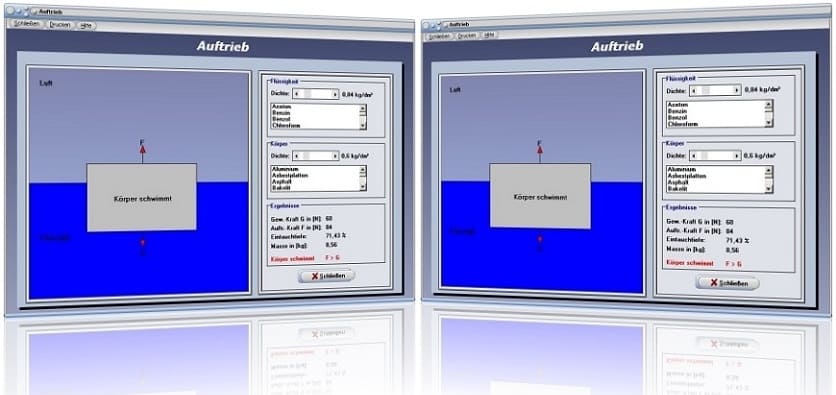
Modul Auftrieb
Das Unterprogramm [Mechanik I] - [Auftrieb] ermöglicht die Untersuchung der Gesetzmäßigkeiten, welche beim Auftrieb in Flüssigkeiten herrschen.
Auftrieb - Abbildung 1
Auftrieb - Abbildung 2
Als Hydrostatik wird die Lehre vom Gleichgewicht ruhender Flüssigkeiten bei der Einwirkung externer Kräfte bezeichnet.
Auftrieb: Als statischer Auftrieb (in Flüssigkeiten auch als hydrostatischer Auftrieb bezeichnet) wird eine der Gravitation entgegengerichtet wirksame Kraft auf einen Körper bezeichnet, der sich in einer Flüssigkeit oder einem Gas befindet. Er bewirkt das Schwimmen eines Körpers in einer Flüssigkeit oder das Schweben in einem Gas. Durch ihn hervorgerufen, erfolgt eine Verringerung der Gewichtskraft eines Körpers in einem Fluid. Der Abtrieb definiert denselben physikalischen Effekt, welcher sich jedoch in die entgegengesetze Richtung auswirkt.
Unter der Gewichtskraft eines Körpers wird die auf ihn im Schwerefeld eines Gestirns wirkende Schwerkraft verstanden. Diese Gewichtskraft bewirkt eine Beschleunigung, welche als Fallbeschleunigung bezeichnet wird.
Es gilt:
G = m·g
G: Gewichtskraft des Körpers [N]
m: Masse des Körpers [kg]
g: Fallbeschleunigung [m/s²]
Durch das Eintauchen eines Körpers in eine Flüssigkeit verliert dieser scheinbar an Gewicht. Die dem Körper entgegengerichtete Kraft wird als Gewichtskraft bezeichnet. Sie entspricht der Gewichtskraft der vom Körper verdrängten Flüssigkeit und entsteht als Differenz von Auftriebskraft und Bodendruckkraft. Diese Gesetzmäßigkeit wird als Archimedisches Prinzip oder als Archimedisches Gesetz bezeichnet. Es ist nach dem griechischen Mathematiker und Physiker Archimedes von Syrakus (um 287 v. Chr. - 212 v. Chr.) benannt, der diesen Zusammenhang als erster formulierte.
Das Archimedisches Gesetz lautet: Beim Eintauchen in eine Flüssigkeit erfährt jeder Körper eine nach oben gerichtete, der Schwerkraft entgegen wirkende Auftriebskraft.
Als Auftriebskraft wird diejenige Kraft bezeichnet, die wirkt, wenn eine Flüssigkeit oder ein Gas von einem Körper verdrängt wird. Die auf einen, sich in einer Flüssigkeit oder einem Gas befindenden, Körper wirkende Auftriebskraft entspricht der Gewichtskraft der von ihm verdrängten Flüssigkeitsmenge bzw. Gasmenge.
Verdrängung: Das Volumen der hierbei verdrängten Flüssigkeit bzw. des hierbei verdrängten Gases (verdrängtes Volumen oder Verdrängungsvolumen) kommt dem Volumen des eingetauchten Körpers gleich. Es gilt die Formel:
FA = Fg
bzw.
FA = V·ρ·g
Hierbei sind:
FA: Auftriebskraft [N]
Fg,Gk: Gewichtskraft des Körpers [N]
V: Volumen der vom Körper verdrängten Flüssigkeit (Verdrängungsvolumen) [m³]
ρ: Dichte der Flüssigkeit [kg/dm³]
g: Fallbeschleunigung [m/s²]
Unter dem Wasservolumen V wird ein nach Raummaß bestimmter Körper bezeichnet, der aus Wasser besteht. Es wird in Kubikmetern (Litern) angegeben.
Auswirkungen des Auftriebs
Hinsichtlich seiner Auswirkungen bestehen je nach der Größe der Auftriebskraft FA bei einem Körper mit der Gewichtskraft Gk folgende Möglichkeiten:
FA < Gk: Sinken (tauchen): Der Körper sinkt zu Boden.
FA = Gk: Schweben (Schwebezustand): Der Körper bleibt vollständig eingetaucht und schwebt.
FA > Gk: Steigen und schwimmen: Der Körper steigt nach oben, taucht nur zum Teil ein
und schwimmt.
FA: Auftriebskraft [N]
Gk: Gewichtskraft des Körpers [N]
Als Schwimmkörper (Auftriebskörper oder schwimmender Körper) wird ein Gebilde bezeichnet, der aufgrund seines Auftriebs durch Verdrängung gemäß dem archimedischen Prinzip selbständig schwimmfähig ist. Schwimmt ein Körper in einer Flüssigkeit, so befinden sich die in der Flüssigekit wirkende Auftriebskraft sowie seine Gewichtskraft im Gleichgewicht.
Schwebender Körper: Ein Körper schwebt in einer Flüssigkeit, wenn die Gewichtskraft die gleiche Größe wie die Auftriebskraft besitzt.
Mit dem Begriff Schwimmstabilität wird das Verhalten eines in einer Flüssigkeit schwimmenden Körpers hinsichtlich seiner Lage zur Oberfläche dieser Flüssigkeit bezeichnet.
Eintauchtiefe
Die Eintauchtiefe (Tiefe oder Tiefgang) beschreibt den Abstand zwischen der Unterkante eines eintauchenden Körpers und dem Flüssigkeitsstand.
Beispiel:
Es gilt, die Eintauchtiefe (den Tiefgang) eines quaderförmigen Körpers mit einer Dichte von 0,28 g/cm3 zu ermitteln, der mit seiner Grundseite in Wasser gelegt wird. Er besitze die Abmaße a = 50 cm, b = 45 cm und h = 12 cm. Die Dichte des Wassers beträgt 1 g/cm3.
Das Archimedische Prinzip besagt, dass der Auftrieb, den ein Körper erfährt der in Wasser gelegt wird, dem Gewicht entspricht, welches das von ihm verdrängte Wasser besitzt. Somit kann Zur Ermittlung der Eintauchtiefe folgende Vorgehensweise angewandt werden.
1. Berechnung des Volumens des eingetauchten Körpers (Volumenverdrängung):
Das Volumen des Körpers beträgt: V = a·b·h = 50 cm·45 cm·12 cm = 27000 cm3.
2. Berechnung der Masse des eingetauchten Körpers:
Die Masse des Körpers beträgt: m = V·ρ = 27000 cm3 ·0,28 g/cm3 = 7560 g
3. Berechnung der Eintauchtiefe t des Körpers:
Da die Masse des eingetauchten Körpers der Masse des von ihm verdrängten Wassers entspricht, gilt für die Eintauchtiefe t des Körpers:
MasseKörper = VolumenKörper · DichteWasser
und somit:
mKörper = a·b·t·ρWasser
Durch Umstellung der obigen Gleichung kann die Eintauchtiefe t des Körpers wie folgt berechnet werden:
t = mKörper/(a·b·ρWasser)
Somit beträgt die Eintauchtiefe dieses Körpers in Wasser im vorliegenden Fall:
t = 7560 g / (50 cm·45 cm·1 g/cm3) = 3,36 cm
Programmbedienung
Um oben aufgeführte Sachverhalte zu untersuchen, stellen Sie mit den dafür vorgesehenen Rollbalken die Dichte der Flüssigkeit, sowie die Dichte des Körpers ein. Das Programm ermittelt daraufhin ob der Körper sinkt, schwimmt oder schwebt. Alternativ zur Einstellung der Dichte per Rollbalkenpositionierung können Sie auch durch einen Klick auf einen Eintrag in den dafür vorgesehenen Auswahllisten einen Stoff selektieren.
Die entsprechende Rollbalkenposition wird der Dichte des ausgewählten Stoffs angepasst.
Dichte - Dichte von Stoffen - Berechnung
Als Dichte wird das Verhältnis der Masse eines Körpers zu seinem Volumen bezeichnet. Die Dichte gasförmiger Stoffe ist druck- und temperaturabhängig. Die Dichte flüssiger und fester Stoffe ist temperaturabhängig.
Die Masse m eines Körpers ist proportional zu seinem Volumen V. Es gilt:
m ~ V
Die Dichte eines Stoffes ist der Quotient aus dessen Masse und seinem Volumen. Es gilt:
ρ = m/V
ρ: Dichte [kg/dm³]
m: Masse [kg]
V: Volumen [dm³]
Wichte ist ein nicht mehr verwendeter Begriff. Er beschreibt das Verhältnis der Gewichtskraft eines Körpers zu seinem Volumen. Da die Dichte gasförmiger Stoffe sowohl druck- wie auch temperaturabhängig ist, beziehen sich derartige Angaben auf die festgelegte Normdichte ρ0 bei 0°C und einem Druck von 1013,25 hPa.
Die mittlere Dichte (durchschnittliche Dichte) mehrerer Stoffe errechnet sich unter Berücksichtigung der einzelnen Volumenanteile und Dichten der entsprechenden Stoffe wie folgt:
ρm: Mittlere Dichte mehrerer Stoffe [kg/dm³]
ρ1,ρ2: Dichte einzelner Stoffe [kg/dm³]
V1,V2: Volumen einzelner Stoffe [dm³]
Dichte - Bestimmung - Dichtebestimmung - Dichtemessung - Dichteberechnung
Dichtebestimmung und Dichteberechnung:
Nachfolgend wird auf das Messen der Dichte (Dichtemessung bzw. das Bestimmen der Dichte) fester Körper und Flüssigkeiten eingegangen.
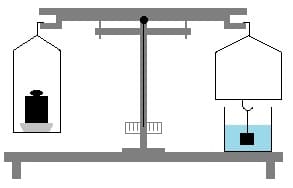
Zur Bestimmung der Dichte fester Körper wird eine hydrostatische Waage (siehe obige Abb.) verwendet. Voraussetzung zur Anwendung dieses Verfahrens ist, dass der Körper vollständig in der Flüssigkeit versinkt. Es gilt:
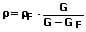
ρ: Zu ermittelnde Dichte des Körpers
ρF: Dichte der Flüssigkeit in welcher sich der Körper befindet
G: Gewichtskraft des Körpers außerhalb der Flüssigkeit
GF: (Scheinbare) Gewichtskraft des Körpers bei vollständigem Eintauchen in Flüssigkeit
Zur Bestimmung der Dichte von Flüssigkeiten kann als Dichtemessgerät ebenfalls eine hydrostatische Waage verwendet werden. Es wird auch in diesem Fall ein fester Körper benutzt, der in keiner der beiden Flüssigkeiten schwimmt oder schwebt. Hierbei gilt:
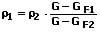
ρ1: Zu ermittelnde Dichte der Flüssigkeit 1
ρ2: Bekannte Dichte einer Flüssigkeit 2
ρF: Dichte der Flüssigkeit in welcher sich der Körper befindet
G: Gewichtskraft des Körpers außerhalb der Flüssigkeit
GF1: (Scheinbare) Gewichtskraft des Körpers bei vollständigem Eintauchen in Flüssigkeit 1
GF2: (Scheinbare) Gewichtskraft des Körpers bei vollständigem Eintauchen in Flüssigkeit 2
Dichte - Einheiten - Umrechnung - Umrechnen
Nachfolgend aufgeführt finden Sie eine Tabelle (Umrechnungstabelle) verwendeter Dichteeinheiten. Diese enthält den entsprechenden Umrechnungsfaktor zur Wandlung derer in die SI-Einheit kg/m³. Die Umrechnung derer kann gemäß den entsprechenden Einträgen unter einer Verwendung des relevanten Faktors erfolgen.
| Bezeichnung der Einheit | Einheit | In die SI-Einheit gewandelt |
| Kilogramm pro Kubikmeter | kg/m3 | 1 kg/m3 |
| Kilogramm pro Kubikdezimeter | kg/dm3 | 1000 kg/m3 |
| Kilogramm pro Liter | kg/l | 1000 kg/m3 |
| Gramm pro Kubikmeter | g/m3 | 0,001 kg/m3 |
| Gramm pro Kubikdezimeter | g/dm3 | 1 kg/m3 |
| Ounce (av.) per cubic foot | oz/ft3 | 1,00115 kg/m3 |
| Ounce (av.) per cubic inch | oz/in3 | 1729,99 kg/m3 |
| Pound mass per cubic foot | lbm/ft3 | 16,0185 kg/m3 |
| Pound mass per cubic inch | lbm/in3 | 2,76799·104 kg/m3 |
| Pound mass per cubic yard | lbm/yd3 | 0,593276 kg/m3 |
| Pound mass per gallon (UK) | lbm/gal | 99,7763 kg/m3 |
| Pound mass per gallon (US) | lbm/gal | 119,826 kg/m3 |
| Slug per cubic foot | slug/ft3 | 515,379 kg/m3 |
| Slug per cubic inch | slug/in3 | 8,90575·105 kg/m3 |
| Slug per cubic yard | slug/yd3 | 19,0881 kg/m3 |
Dichte einiger Flüssigkeiten
In der folgenden Tabelle (Dichtetabelle) ist die Dichte einiger flüssiger Stoffe (Flüssigkeiten) aufgeführt (bei 20°C):
| Flüssigkeit | Dichte in g/cm³ |
| Aceton | 0,791 |
| Benzin (Flugzeug) | 0,72 |
| Benzin (Fahrzeug) | 0,78 |
| Benzol | 0,879 |
| Chloroform | 1,489 |
| Diesel (Kraftstoff) | 0,86 |
| Erdöl | 0,73 ... 0,94 |
| Glycerin | 1,261 |
| Heizöl | 0,95 ... 1,09 |
| Milch | 1,032 |
| Natronlauge (40%,16°C) | 1,434 |
| Oktan | 0,702 |
| Petroleum | 0,81 |
| Quecksilber | 13,546 |
| Salzsäure (40%) | 1,195 |
| Schwefelsäure (50%) | 1,31 |
| Spiritus | 0,83 |
| Wasser | 0,9982 |
Dichte einiger fester Stoffe
In der folgenden Tabelle (Dichtetabelle) ist die Dichte einiger fester Stoffe aufgeführt:
| Fester Stoff | Dichte in g/cm³ |
| Aluminium | 2,702 |
| Asphalt | 1,1 ... 2,9 |
| Bauxit | 2,4 ... 2,6 |
| Bernstein | 1,0 ... 1,1 |
| Bimsstein | 0,37 ... 0,9 |
| Blei | 11,35 |
| Braunkohle | 1,2 ... 1,4 |
| Bronze | 8,7 ... 8,9 |
| Diamant | 3,51 |
| Eis (0°C) | 0,917 |
| Eisen (Roheisen grau) | 6,6 ... 7,4 |
| Eisen (Roheisen weiß) | 7,6 ... 7,8 |
| Germanium | 5,35 |
| Glas (Fenster) | 2,48 |
| Glas (Flasche) | 2,6 |
| Gold | 19,29 |
| Granit | 2,6 ... 3,0 |
| Graphit | 2,0 ... 2,5 |
| Grauguss | 7,2 |
| Gummi | 0,92 |
| Hartgummi | 1,1 ... 1,3 |
| Iridium | 22,42 |
| Kalkspat | 2,6 ... 2,8 |
| Konstantan | 8,8 |
| Keramik | 2,1 ... 2,3 |
| Kupfer (rein) | 8,933 |
| Leder (trocken) | 0,9 ... 1,0 |
| Leim | 1,27 |
| Lehm | 1,5 ... 1,8 |
| Magnesium | 1,74 |
| Marmor | 2,6 ... 2,8 |
| Messing | 8,1 ... 8,6 |
| Molybdän | 10,21 |
| Natriumchlorid (Salz) | 2,17 |
| Neusilber | 8,3 ... 8,7 |
| Nickel | 8,8 |
| Papier | 0,7 ... 1,2 |
| Plexiglas | 1,2 |
| Platin | 21,4 |
| Polyamid | 1,08 ... 1,14 |
| Polystyrol | 1,05 ... 1,2 |
| PVC | 1,38 |
| Porzellan | 2,3 ... 2,5 |
| Sand (erdfeucht) | 2,0 |
| Schaumstoff | 0,02 ... 0,05 |
| Schiefer | 2,7 ... 2,8 |
| Silber | 10,5 |
| Stahl | 7,7 ... 8,1 |
| Steinkohle | 1,2 ... 1,4 |
| Wofram | 19,3 |
| Ziegelstein | 1,3 ... 1,6 |
| Zinn | 7,2 |
Dichte einiger Gase (gasförmiger Stoffe)
In der folgenden Tabelle (Dichtetabelle) ist die Dichte (Normdichte) einiger gasförmiger Stoffe (Gase) aufgeführt (bei 0°C und 101,3 Pa):
| Gas | Dichte in kg/m³ |
| Ammoniak | 0,7714 |
| Argon | 1,786 |
| Butan | 2,709 |
| Chlor | 3,214 |
| Chlorwasserstoff | 1,489 |
| Helium | 0,1785 |
| Kohlendioxid | 1,9769 |
| Kohlenmonoxid | 1,25 |
| Krypton | 3,744 |
| Luft | 1,2929 |
| Methan | 0,7168 |
| Neon | 0,9002 |
| Propan | 2,0096 |
| Sauerstoff | 1,42895 |
| Stickstoff | 1,2505 |
| Wasserstoff | 0,08988 |
| Xenon | 5,897 |
Auftrieb - Abbildung 3
Auftrieb - Abbildung 4
Auftrieb - Abbildung 5
Auftrieb - Abbildung 6
Auftrieb - Abbildung 7
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu nützlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Kurzbeschreibungen von Modulen zum Themengebiet Mechanik - Kurzbeschreibungen von Modulen zum Themengebiet Elektrotechnik - Kurzbeschreibungen von Modulen zum Themengebiet Optik - Kurzinfos zum Themengebiet Thermodynamik sowie unter Kurzbeschreibungen von Modulen zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Statischer Auftrieb und Wikipedia - Archimedisches Prinzip zu finden.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Schräger Wurf - Schiefer Wurf, Waagerechter Wurf - Horizontaler Wurf, Hookesches Gesetz, Mechanische Arbeit, Zweites Newtonsches Gesetz, Drittes Newtonsches Gesetz, Gedämpfte mechanische Schwingung, Bewegungen auf einer Kreisbahn, Hebelgesetz, Chaotisches Doppelpendel, Mathematisches Pendel, Freier Fall und Luftwiderstand, Harmonische Schwingungen, Molekularbewegungen, Brownsche Bewegungen, Potentielle und kinetische Energie, Ideale Strömung - Volumenstrom, Druck in Flüssigkeiten, Wellen - Simulationen, Zusammengesetzte Bewegung, Bewegungen in der Ebene, Carnotscher Kreisprozess, Adiabatische Zustandsänderung, Isotherme Zustandsänderung, Isobare Zustandsänderung, Isochore Zustandsänderung, Beugung am Spalt, Hohlspiegel, Sammellinse, Zerstreuungslinse, Wechselstromkreise, RLC-Kreis - RLC-Schaltung, RL-Kreis - RL-Schaltung, RC-Kreis - RC-Schaltung, Resonanz - Resonanzkurve, Widerstände im Wechselstromkreis, Schwingungen und deren Überlagerung, Plattenkondensator, Ladung und Entladung von Kondensatoren, Reihenschaltung und Parallelschaltung, Lissajou-Figuren, 1. Keplersches Gesetz, 2. Keplersches Gesetz, 3. Keplersches Gesetz
4-Takt-Ottomotor - Impulssatz - Gleichförmige und gleichförmig beschleunigte Bewegung - Bewegung und Geschwindigkeit - Geschwindigkeit und Beschleunigung - Wellen - Druck in Flüssigkeiten - Ideale Strömung - Kinetische und potentielle Energie - Brownsche Bewegung - Molekularbewegung - Harmonische Schwingungen - Kreisbahnbewegung - Geneigte Ebene - Freier Fall - Waagerechter und schiefer Wurf - Pendel - Chaos-Doppelpendel - Gedämpfte mechanische Schwingung - Rolle und Flaschenzug - Balkenwaage - Hebelgesetz - Zweites Newtonsches Gesetz - Drittes Newtonsches Gesetz - Mechanische Arbeit - Hookesches Gesetz
Unterprogramm Auftrieb
PhysProf 1.1 - Unterprogramm RLC-Kreis
MathProf 5.0 - Unterprogramm Kurven in Parameterform
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Physik interaktiv
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm,welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
Eine Übersicht aller in MathProf 5.0 zur Verfügung stehender Programmteile finden Sie im MathProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
