Startseite » MathProf - Module zum Fachthemengebiet Vektoralgebra

Kurzinfos zum
Themengebiet Vektoralgebra

Nachfolgend aufgeführt finden Sie Bilder und Kurzbeschreibungen zu
einigen Modulen, die im Programm MathProf 5.0 unter dem
dem Hauptmenüpunkt Vektoralgebra implementiert sind.

• Gerade und Vektoren

Durchführung von Untersuchungen mit einer Geraden und Vektoren, die zur Definition einer Geradengleichung in Vektorform in der Ebene führen.

Gerade und Vektoren - Bild 2 - Vektoren - Stützvektor - Ortsvektor - Richtungsvektor - Vektorgleichung - Vektordarstellung - Vektorielle Darstellung - Grafisch - Vektorgleichung einer Geraden - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

• Vektorielle Linearkombination

Analyse der Zusammenhänge bei der Bildung einer Linearkombination zweier Vektoren in der Ebene.

Vektorielle Linearkombination - Bild 2 - Linear abhängige Vektoren - Grafik - Vektoren - Ortsvektor - Graph - Skalar - Parameter - Zeichnen - Rechner - Berechnen - Grafisch - Bilder - Darstellung - Berechnung - Darstellen - Lineare Abhängigkeit

• Vektoraddition in der Ebene

Interaktive Verdeutlichung der Zusammenhänge bei der Addition von Vektoren in der Ebene.

Vektoraddition in der Ebene - Bild 2 - Vektoren - Zeichnerische Darstellung - Zeichnerisch addieren - Winkel zwischen Vektoren - Länge von Vektoren - Länge eines Vektors - Vektoren im R2 - Vektoren 2D - Betrag eines Vektors - Winkelberechnung - Winkelbestimmung - Abstand zwischen zwei Punkten - Basisvektoren - Vektorielle Addition - Resultierende - Gegenvektor - Verbindungsvektor - Kräfteaddition - Rechenoperationen - Vektorsumme - Summe von Vektoren - Darstellung von Kräften - Vektoren und Koordinaten - Vektoren grafisch addieren - Geometrische Addition - Geometrische Darstellung - Geometrisch addieren - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

• Resultierende

Interaktive, geometrische Ermittlung der Resultierenden zweier Vektoren in der Ebene.

Resultierende - Bild 2 - Vektorzerlegung - Vektorbetrag - Zeichnen - Graph - Grafisch - Bilder - Darstellung - Richtung - Berechnen - Darstellen - Rechner - Plotten - Zerlegung von Vektoren - Resultierende berechnen - Summenvektor

• Vektorprodukt, Skalarprodukt, Spatprodukt, Vektorprojektion, Tripelprodukt

Numerische Ermittlung von Berechnungsergebnissen und grafische Darstellung der Zusammenhänge zu den Themenbereichen Vektorprodukt, Skalarprodukt, Spatprodukt, Vektorprojektion und Tripelprodukt.

Vektorprodukt - Vektorielles Produkt - Kreuzprodukt - Äußeres Produkt - Vektoren - Betrag - Formel - Eigenschaften - Gleichung - Grafisch - Bilder - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

Spatprodukt - Spat - Volumen - Spatvolumen - Vektorrechnung - Parallelepiped - Gemischtes Produkt - Vektoren - Betrag - Formel - Eigenschaften - Gleichung - Grafisch - Bilder - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

• Vektoraddition im Raum

Analyse der Zusammenhänge bei Durchführung einer Vektoraddition im Raum. Komponentenweise Aufsummierung, der durch Punkte definierten Vektoren und Ermittlung der Resultierenden des Systems.

Vektoraddition im Raum - Bild 2 - 3D-Vektoren zeichnen - Darstellung kollinearer Vektoren - Darstellung komplanarer Vektoren - Resultierende - Räumlicher Vektor - Raum - Räumlich - Rechner - Grafik - R3 - Graph - Grafisch - Plotten - Plotter - Bilder - Darstellung - Winkelberechnung - Berechnung - Darstellen - Zeichnen - Dreidimensionaler Vektor - Grafische Addition von Vektoren

• Geraden im Raum (Punkt-Richtungs-Form und 2-Punkte-Form)

Darstellung und numerische Analysen von Geraden (sowie Punkten) im Raum sowie die Durchführung der:

Eigenschaftsanalyse einer Gerade (Richtungswinkel der Gerade, Spurpunkte der Gerade, Abstand der Gerade vom Koordinatenursprung, Gleichung der Geraden in versch. Darstellungsformen)
Berechnung des Abstands eines Punktes von einer Geraden
Ermittlung des Schnittpunkts und des Schnittwinkels zweier Geraden bzw. des Abstands zweier Geraden

Geraden im Raum - Bild 1 - Geraden im Raum - 3D - Windschiefe Geraden - Schnittwinkel - Parameterdarstellung - Parameterform - Geradengleichung - Punkt-Richtungsform - Windschiefe Geraden - Schnittpunkt zweier Geraden - Normalabstand - Bild - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

Geraden im Raum - Bild 2 - Gerade - Vektoren - 3D - Vektordarstellung - Zweipunktegleichung - Geradengleichung - Spurpunkte - Richtungsvektor - Ortsvektor - Abstand zweier Geraden - Abstand zweier Punkte - Schnittpunkt zweier Geraden - Raum - Schnittwinkel - Verbindungsvektor - Schnittpunkt Gerade-Gerade - Winkel - Abstand - Lot - Gleichung - Grafik - Raum - Räumlich - Plotter - Rechner - Berechnen - Graph - Beispiel - Zeichnen - Plotten - Darstellen

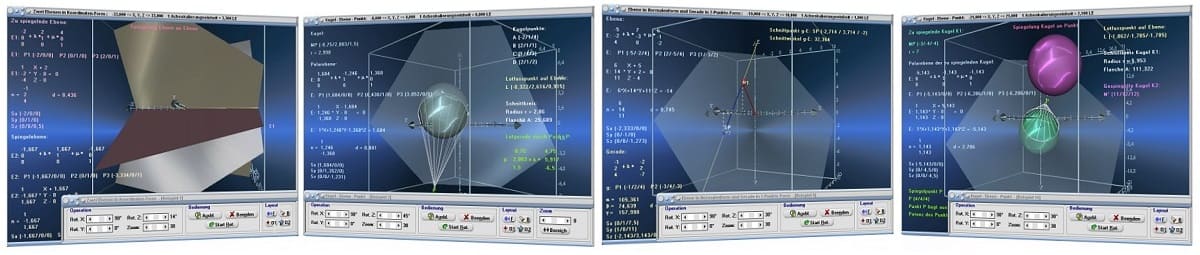
• Ebenen im Raum (Punkt-Richtungs-Form, 3-Punkte-Form, Normalenform und Koordinatenform)

Darstellung und numerische Analysen von Ebenen im Raum sowie die Durchführung der:

Analyse der Eigenschaften einer Ebene (Gleichung der Ebene in versch. Darstellungsformen, Spurpunkte der Ebene, Abstand einer Ebene vom Koordinatenursprung)
Berechnung des Abstands eines Punktes von einer Ebene
Ermittlung des Schnittpunkts und des Schnittwinkels einer Ebene und einer Geraden
Ermittlung des Abstands einer Geraden zu einer Ebene

Ebenen - Bild 1 - Vektorielle Darstellung - Ebenengleichungen - Parameterform - Ebenengleichung - Parametergleichung - Winkel - Spurpunkte - Schnittpunkte - Abstand - Stützvektor - Spannvektoren - Abstandsberechnung - Parameter - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

Ebenen - Bild 2 - Ebene - Gerade - Raum - 3D - Schnitt - Parallel - N-Vektor - Normalenvektor - Durchstoßpunkt - Spurpunkte - Schnittpunkt - Parameterform - Normalenform - Vektoren - Abstandsberechnung - Abstand - Bild - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

Ebenen - Bild 3 - Punkt - Abstand - Lotgerade - Gleichung - Koordinatengleichung - Lotvektor - Normalenvektor - Ebene im Raum - Formel - Winkel - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Plotter

Ebenen - Bild 4 - Lagebeziehung - Ebenengleichungen - Schnitt - Schnittgerade - 3D - Schnittwinkel - Gleichung - Spiegeln - Spiegelung - Ebenenspiegelung - Lagebeziehung - Schneiden - Winkel - Windschiefe Ebenen - Abstand - Spurpunkte - Spurgerade - Spiegelebene - Spiegelung - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

• Kugel - Gerade

Durchführung von Untersuchungen mit Geraden im Raum (Punkt-Richtungs-Form und 2-Punkte-Form) und Kugeln (vektorielle Form, 4-Punkte-Form). Hierzu gehören u.a.:

Ermittlung der Schnittpunkte einer Geraden und einer Kugel
Ermittlung der Sehnenlänge (Bereich einer Geraden, der innerhalb einer Kugel liegt)
Durchführung der Spiegelung einer Kugel an einer Geraden

Kugel und Gerade - Bild 1 - Schnittpunkt - Abstand - Lagebeziehung - Lage - Kugelgleichung - Schnittpunkte - Kugel durch 4 Punkte - Abstand Kugel-Gerade - Richtungswinkel - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

Kugel und Gerade - Bild 2 - Punktrichtungsform - Eigenschaften - Kugelgleichung - Raum - Mittelpunkt - Zweipunkteform - Berührpunkt - Durchstoßpunkt - Spiegeln - R3 - Spiegelung - Schnittpunkte - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

Kugel und Gerade - Bild 3 - Schnittpunkt - Abstand - Lagebeziehung - Lage - Kugelgleichung - Schnittpunkte - Kugel durch 4 Punkte - Abstand Kugel-Gerade - Richtungswinkel - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

Kugel und Gerade - Bild 4 - Punktrichtungsform - Eigenschaften - Kugelgleichung - Raum - Mittelpunkt - Zweipunkteform - Berührpunkt - Durchstoßpunkt - Spiegeln - R3 - Spiegelung - Schnittpunkte - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

• Kugel - Kugel

Durchführung von Untersuchungen mit zwei Kugeln (vektorielle Form, 4-Punkte-Form). Hierzu gehören u.a.:

Ermittlung der Eigenschaften des Schnittkreises zweier Kugeln
Ermittlung der Eigenschaften der Schnittebene/Potenzebene zweier Kugeln

Kugeln - Bild 1 - Berührpunkt - Kugel berechnen - Potenzebene einer Kugel - Lage zweier Kugeln - Formel - Schnitt zweier Kugeln - Gegenseitige Lage von Kugeln - Kugelgleichungen - Kugelberechnung - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

Kugeln - Bild 2 - Kugelschnitt - Kugelgleichung im Raum - Dreidimensional - 3D - Bild - Grafik - Darstellung - Berechnung - Berechnen - Rechner - Formeln - Plotten - Graph - Gleichung - Darstellen - Lage Kugel Kugel - Plotten

• Kugel - Ebene- Punkt

Durchführung von Untersuchungen mit Ebenen (Punkt-Richtungs-Form, 3-Punkte-Form, Normalen-Form und Koordinatenform) und Kugeln in vektorieller Form oder 4-Punkte-Form) sowie Punkten. Hierzu zählen u.a.:

Ermittlung der Eigenschaften des Schnittkreises einer Kugel und einer Ebene
Ermittlung der Eigenschaften der Polarebene eines Punktes und einer Kugel
Ermittlung der Eigenschaften der Tangentialebenen einer in 4-Punkte-Form definierten Kugel in den Kugelpunkten
Eigenschaftsanalyse von Polarebenen, Tangentialebenen und Schnittebenen
Spiegelung einer Kugel an einer Ebene

Kugel - Ebene - Punkt - Bild 1 - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

Kugel - Ebene - Punkt - Bild 2 - Abstand - Distanz - Tangentialebene - Tangentialkegel - Schnittkreis - Gleichung - Schnittkreis Kugel Ebene - Schnittebene - Polarebene - Kugelgleichungen - Spiegelung - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

Kugel - Ebene - Punkt - Bild 3 - Spiegelung - Spiegeln - Tangentialkegel - Schnittkreis - Darstellen - Plotten - Graph - Rechner - Berechnen - Grafik - Zeichnen - Plotter

Kugel - Schnitt - Schneiden - Grafik - Plotter

Implementierte Module zum Themenbereich Vektoralgebra

Gerade und Vektoren - Vektorielle Linearkombination - Vektorielles Teilverhältnis - Vektoraddition in der Ebene - Resultierende - Komponentendarstellung (3D) - Vektorprodukt (3D) - Skalarprodukt (3D) - Spatprodukt (3D) - Vektorprojektion (3D) - Tripelprodukt (3D) - Numerische Vektoraddition im Raum - Grafische Vektoraddition im Raum (3D) - Gerade in Punkt-Richtungs-Form (3D) - Gerade in 2-Punkte-Form (3D) - Ebene in Punkt-Richtungs-Form (3D) - Ebene in 3-Punkte-Form (3D) - Ebene in Normalen-Form (3D) - Ebene in Koordinaten-Form (3D) - Zwei Ebenen (3D) - Kugel - Gerade (3D) - Kugel - Ebene - Punkt (3D) - Kugel - Kugel (3D)

Weitere relevante Seiten zu diesem Programm

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Videoauswahl zu MathProf 5.0.

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche können Sie eine kostenlose Demoversion des Programms MathProf 5.0 herunterladen.

Zum Download der Demoversion von MathProf 5.0

Durch die Ausführung eines Klicks auf die entsprechende nachfolgend gezeigte Schaltfläche gelangen Sie zum Inhaltsverzeichnis der in MathProf 5.0 implementierten Module bzw. zur Bestellseite für das Programm.

MathProf 5.0 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich mathematische Sachverhalte auf einfache Weise zu verdeutlichen. Zudem spricht es diejenigen an, die sich für Mathematik interessieren, oder mathematische Probleme verschiedenster Art zu lösen haben und von grafischen 2D- und 3D-Echtzeitdarstellungen sowie Animationen beeindruckt sind.

Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.

Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.

Kurzinfos zu Inhalten einiger Unterprogramme erhalten Sie unter:

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Analysis eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Vektoralgebra eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

II - PhysProf 1.1
Physik interaktiv

PhysProf 1.1 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich physikalische Gesetzmäßigkeiten und Gegebenheiten zu verdeutlichen. Es spricht alle an, die sich für die Ergründung physikalischer Prozessabläufe und derartige Zusammenhänge interessieren. In zahlreichen Unterprogrammen besteht die Möglichkeit, Veränderungen von Einflussgrößen manuell, oder durch die Ausgabe automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren. Inhaltlich umfasst es ca. 70 verschiedene Unterprogramme zu den Fachthemenbereichen Mechanik, Elektrotechnik, Thermodynamik und Optik.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

III - SimPlot 1.0
Visualisierung und Simulation interaktiv

SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.

Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.

SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.

Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.

Eine Inhaltsübersicht dessen finden Sie unter SimPlot - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

Beispiele einiger mit Simplot 1.0 erzeugter Grafiken finden Sie unter Beispiele, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen mit SimPlot erzeugten Animationen finden Sie unter SimPlot-Videos, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.