MathProf - Zinsrechner - Tageszinsen - Jahreszins - Zahlung - Rechner

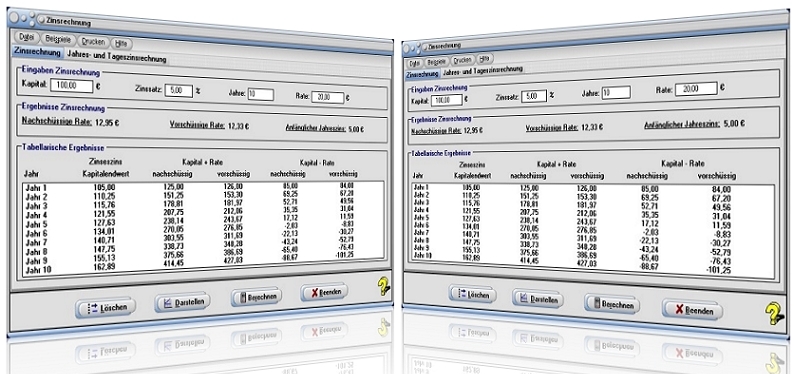
Modul Zinsrechnung

---

 
Mit Hilfe des Programmteils [Sonstiges] - Zinsrechnung können Zinsrechnungen, Jahreszinsrechnungen und Tageszinsrechnungen durchgeführt werden.
 

1. Zinsrechnung (Verzinsung)

 
Nach einer Wahl des Registerblatts Zinsrechnung wird die Ausführung von Zinsrechnungen ermöglicht.
 

  

Folgende Werte werden bei der Berechnung von Zinsen in diesem Modul ermittelt:

• Nachschüssige Rate
• Vorschüssige Rate
• Anfänglicher Jahreszins

Zudem werden tabellarisch (jahresbezogen) ausgegeben:

• Zinseszins (Kapitalendwert) pro Jahr
• Endbetrag bei nachschüssiger Ratenzahlung (Kapital + Rate)
• Endbetrag bei vorschüssiger Ratenzahlung (Kapital + Rate)
• Endbetrag bei nachschüssiger Ratenzahlung (Kapital - Rate)
• Endbetrag bei vorschüssiger Ratenzahlung (Kapital - Rate)

 

Vorschüssig (praenumerando): Erfolgt eine Kapitalmehrung / Kapitalminderung in Form der Zahlung / Abhebung einer Rate (fester Betrag) zu Anfang eines Jahres, so wird diese als vorschüssig oder als vorschüssige Verzinsung bezeichnet.

 

Nachschüssig (postnumerando): Erfolgt eine Kapitalvermehrung / Kapitalminderung in Form der Zahlung /  Abhebung einer Rate (fester Betrag) zu Ende eines Jahres, so wird diese als nachschüssig oder als nachschüssige Verzinsung bezeichnet.
 

  
Als Kapital wird derjenige Geldbetrag bezeichnet, den ein Geldgeber einem Kreditnehmer gegen die Entrichtung zuvor festgelegter Zinsen zu Beginn einer Verzinsungsperiode überlässt.

Nachfolgend aufgeführt sind die Zinsformel (Jahreszinsformel) sowie Formeln zur Berechnung der Zinsen, des Kapitals, des Zinssatzes sowie der Zeit. Diese bilden die Grundlagen der einfachen Zinsrechnung.

Die Zinsformel lautet:


bzw.



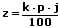
Formeln zur Berechnung der Zinsen, des Kapitals, des Zinssatzes sowie der Zeit:
 

Berechnung	für j Jahre	für m Monate	für t Tage
der Zinsen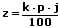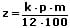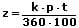
des Kapitals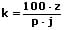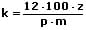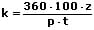
des Zinssatzes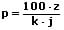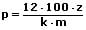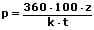
der Zeit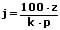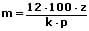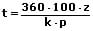

mit:
k: Kapital
z: Zinsen
j: Anzahl der Jahre
p: Zinssatz

Zinsen werden unter anderm mit Prozentangaben angegeben. Als Zinsfuß (auch Prozentzahl) wird die Zahl bezeichnet, welche sich vor dem Prozentzeichen einer Prozentangabe befindet.

Zinssätze: Der Zinssatz ist die Angabe einer Zahl gemeinsam mit dem Prozentzeichen. Eine Zinsangabe in Form einer Prozentzahl lautet beispielweise: 5%.

Einfache Verzinsung: Bei der einfachen Zinsrechnung bleibt der Zinsbetrag über die gesamte Laufzeit konstant. Das Kapital, auf welches sich der zugrundegelegte Zinssatz bezieht, verändert sich innerhalb dieses Zeitraums nicht.
 

Zinsrechnungen: Als Zinsrechnung (Zinsberechnung) wird eine Methode zur Berechnung von Zinsen in Abhängigkeit von eingesetztem Kapital bezeichnet. Dies wird für einen festgelegten Zinssatz sowie eine bestimmte Laufzeit durchgeführt.

Die Zinsrechnung unterscheidet zwischen der einfachen Zinsrechnung und der Zinseszinsrechnung. Zudem wird zwischen einer Zinsrechnung mit Durchführung einer einmaligen Zinsberechnung sowie einer Zinsrechnung mit mehrmaliger Zinsberechnung unterschieden.
 
Zins (Zinsen): Als Zins (Zinsen) wird das Entgelt bezeichnet, das ein Schuldner einem Gläubiger als Gegenleistung für vorübergehend überlassenes Kapital zahlt.

Zinssatz: Der Zinssatz ist der in Prozent angegebene Preis für Geld oder Kapital der bei einer Bank angelegt wird und verzinst wird.

Zinseszins: Als Zinseszinsen werden im Finanzwesen Zinsen bezeichnet, die Anleger auf ihre Zinsen erhalten. Es sind dem Kapital hinzugefügte Zinsen, die zum geltenden Zinssatz zusammen mit dem Kapital erneut verzinst werden.

Kapitalverzinsung: Mit dem Begriff Kapitalverzinsung wird die Verzinsung des für eine unternehmerische Tätigkeit eingesetzten Kapitals bezeichnet.

Verzinsung: Die Verzinsung einer Geldanlage bezeichnet die Bedingungen unter denen Zinsen als Vergütung für geliehenes Geld berechnet werden. Der Kunde eines Geldinstituts stellt hierbei einen Geldbetrag bereit, der von der Bank gewinnbringend angelegt werden kann.

Lineare Verzinsung: Bei einer linearen Verzinsung wird angelegtes Kapital über einen bestimmten Zeitraum mit einem festgelegten Zinssatz verzinst. Als Grundlage für die jährliche Verzinsung wird das zu Beginn angelegte Startkapital verwendet. Hierdurch bleiben die Zinsen über den festgelegten Zeitraum hinweg, konstant.

Zinserträge: Im Rechnungswesen stellt der Zinsertrag einen periodenbezogenen betrieblichen Ertrag dar, der aus vereinnahmten Zinsen stammt und der in der Kosten- und Leistungsrechnung übernommen wird.

Zinsraten: Als Zinsrate wird die Rate bezeichnet, die für eine Leihgabe in Form von regelmäßigen Zahlungen oder jährlich zu entrichten ist. Sie wird in einem prozentualen Anteil der geliehenen Summe ausgedrückt.

Einfache Zinsrechnung: Bei Durchführung der einfachen Zinsrechnung werden fällige Zinsen am Ende der Laufzeit beispielsweise ausgezahlt und nicht zur Erhöhung des zinsbringenden Kapitals verwendet. Das aus einer einfachen Verzinsung resultierende Endkapital entspricht nach Ablauf des ersten Jahres dem Endkapital nach Durchführung einer Zinseszinsrechnung.

Tageszins: Tageszinsen beziehen sich auf die Verzinsung einer Geldanlage über den Zeitraum eines Tages. Es sind die Zinsen, die binnen eines Tages auf ein eingesetztes Kapital anfallen.

Jahreszins: Jahreszinsen beziehen sich auf die Verzinsung einer Geldanlage über den Zeitraum eines Jahres. Es sind die Zinsen, die binnen eines Jahres auf ein eingesetztes Kapital anfallen.

Jährliche Verzinsung: Bei einer jährlichen Verzinsung wird das angelegte Kapital einmal jährlich, üblicherweise am Ende eines Jahres, verzinst.

Monatliche Verzinsung: Bei einer monatlichen Verzinsung wird das angelegte Kapital einmal monatlich verzinst. Sie wird bei den meisten Anlagen nicht angewandt.

Monatszins: Monatszinsen beziehen sich auf die Verzinsung einer Geldanlage über den Zeitraum eines Monats. Es sind die Zinsen, die binnen eines Monats auf ein eingesetztes Kapital anfallen.

Endsaldo: Als Endsaldo wird die Summe aller Soll- und Habenbeträge für ein Konto bezeichnet. Hierbei ist das Anfangssaldo für den letzten Tag jeder Buchungsperiode mit einzubeziehen.

Tägliche Verzinsung: Bei einer täglichen Verzinsung wird das angelegte Kapital wird einmal täglich verzinst.

Ratenzahlung: Mit einer Ratenzahlung wird die Zahlung eines Geldbetrags in Teilbeträgen (Raten) über einen festgelegten Zeitraum bezeichnet.

Raten: Eine Rate bezeichnet eine für eine Zeitspanne geltende Größe.

Zinsperioden: Mit dem Begriff Zinsperiode wird der Zeitabstand, der zwischen zwei Zinsgutschriften liegt, bezeichnet.

Stetige Verzinsung: Bei einer stetigen Verzinsung strebt die Anzahl der Zinsperioden gegen Unendlich. Die Dauer einer einzelnen Verzinsungsperiode mit anschließender Wiederveranlagung hingegen konvergiert gegen 0. Bei einem Zinssatz i gilt für das Endkapital nach n Jahren in diesem Fall:

K = K₀·e^n-1

K: Endkapital
K₀: Anfangskapital
e: Eulersche Zahl = 2, 718 281 828
i: Zinssatz
n: Jahre

Anfangskapital (Startkapital): Als Anfangskapital oder Startkapital wird der Geldbetrag bezeichnet, den ein Anleger zu Beginn einer Kapitalanlage einbezahlt.

Kapitalertrag: Als Kapitalertrag wird der Ertrag bezeichnet, den eine Kapitalanlage einem Anleger erbringt. Bei diesem kann es sich, anhängig von der Anlageform, um einen Zinsertrag, einen Investmentertrag, einen Gewinn aus Eigenkapital, einen Dividendenertrag, eine Immobilienmiete, ein Pachtzins oder einen Kursgewiinn handeln.

Endkapital: Als Endkapital wird das Vermögen bezeichnet, das am Ende der Laufzeit einer Geldanlage als gewisser Kapitalertrag zur Verfügung steht.

Nominaler Zinssatz (Nominalzinssatz): Unter dem nominalen Zinssatz (Nominalzinssatz) wird derjenige Zinssatz verstanden, welcher zwischen dem Geldgeber und Geldnehmer vereinbart wurde und der gezahlt wird. Hierzu zählt beispielsweise der Zinsertrag, den ein Sparer für seine Einlagen erhält, oder ein Kreditnehmer für seinen erhaltenen Kredit zu zahlen hat. Ein Sparer erhält diesen, ein Kreditnehmer zahlt ihn. Er trägt auch die Bezeichnung nominaler Zins oder Nominalzins.

Stetige Verzinsung: Eine stetige Verzinsung erfolgt nicht innerhalb festgelegter Zeitabstände, sondern vielmehr fortlaufend. Das zu verzinsende Kapital wird kontinuierlich (innerhalb kleinster Zeitperioden) erhöht.
 
Finanzrechner: Bei einem Finanzrechner handelt es sich um einen elektronischen Rechner, mit Hilfe dessen es erleichtert wird, Kreditentscheidungen zu treffen sowie Zusammenhänge und Auswirkungen von Geldgeschäften zu kalkulieren und besser im Voraus zu planen.
 
Finanzierung: Als Finanzierung wird das Bereistellen von Kapital für ein wirtschaftliches Subjekt bezeichnet. Sie kann für Anschaffungen jeglicher Art Verwendung finden. Beispiele hierfür sind unter anderem eine Kreditfinanzierung, eine Baufinanzierung, ein Autokredit oder die Ablösung eines Dispositionskredits. Eine Finanzierung funktioniert in gleicher Weise wie ein Kredit. Es wird ein bestimmter Betrag an Kapital von einem Kreditvermittller geliehen, der über einen vereinbarten Zeitraum hinweg zurückzuzahlen ist.
 
Unterjährige Verzinsung:
Bei einer unterjährigen Verzinsung wird der Zins bereits mehrmals während des laufenden Jahres zum Kapital geschlagen (z.B. monatlich). In diesem Fall ist die effektive Verzinsung höher als bei der Durchführung einer jährlichen Verzinsung. Es gilt:

K_n = K₀·(1 + p_u/100)
p_u = p/m

Gemischte Verzinsung:
Bei einer gemischten Verzinsung beträgt die Dauer der Vezinsungszeit kein ganzzahliges Vielfaches eines Jahres. Dauert die Verzinsung länger als ein Zeitraum von n Jahren, so gilt es den entsprechenden Teil des angebrochenen Jahres einzuberechnen. Für diesen Zeitraum erfolgt die Berechnung einfacher Zinsen. Aufgrun dieser Tatsache, dass zwei verschiedene Arten der Verzinsung angewandt werden, wird diese Kombination als gemischte Verzinsung bezeichnet. In diesem Fall gilt:

K_n = K₀·(1 + _pu/100)^n_v · (1 + p_u/100·n_r)
p_u = p/m

K₀: Anfangskapital in €
K_n: Endkapital in €
p: Zinssatz in %
p_u: Unterjähriger Zinssatz in %
m: Anzahl der Zinsperioden je Jahr
n: Anzahl der Jahre der Verzinsung (Laufzeit)
n_v: Anzahl voller Verzinsungsperioden
n_r: Restzeit (in Jahren), bei der mit einfachem Zins gerechnet wird
 
 

 

 

Gehen Sie folgendermaßen vor, um in diesem Modul Zinsberechnungen auszuführen:
 

1. Legen Sie zunächst die Werte für Kapital, Zinssatz (in Prozent) und den zu berechnenden Zeitraum (Jahre) durch die Eingabe entsprechender Werte in die dafür vorgesehenen Felder fest.
    

2. Möchten Sie unter anderem prüfen, wie sich der Betrag einer Restschuld mit dem Verlauf von Jahren ändert, so erreichen Sie dies durch die zusätzliche Festlegung eines entsprechenden Werts für Raten im Eingabefeld Rate. Andernfalls belassen Sie diesen Wert auf 0.
    

3. Nach einer Bedienung der Schaltfläche Berechnen werden oben aufgeführte Werte ermittelt und in den Formularbereichen Ergebnisse Zinsrechnung sowie Tabellarische Ergebnisse ausgegeben.
    

4. Um sich die Zusammenhänge grafisch zu veranschaulichen, bedienen Sie die Schaltfläche Darstellen.
    

2. Tageszinsrechnung - Jahreszinsrechnung

 
Die Wahl des Registerblatts Jahres- und Tagesszinsrechnung ermöglicht das Durchführen von Jahres- und Tageszinsrechnungen.
 

 
Folgende Werte werden bei der Ausführung von Jahreszinsrechnungen ermittelt:

• Zins pro Jahr
• Kapitalendwert

Werden Berechnungen mit Tageszinsen praktiziert, so wird ausgegeben:

• Zins für Zeitraum
• Zins pro Tag

 

 

 
Bei der Praktizierung einer Jahreszinsrechnung geben Sie die Werte für Kapital und Zinssatz (in Prozent) in die dafür vorgesehenen Felder im Formularbereich Jahreszinsrechnung ein und bedienen hierauf die Schaltfläche Berechnen. Die ermittelten Ergebnisse werden im Formularbereich Ergebnisse Jahreszinsrechnung ausgegeben.

Um eine Tageszinsrechnung zu veranlassen, belegen Sie die Eingabefelder Kapital (zu verzinsendes Kapital), Zinssatz (in Prozent) sowie Zeitraum (Anzahl Tage) im Formularbereich Tageszinsrechnung mit den entsprechenden Werten und führen hierauf einen Klick auf die Schaltfläche Berechnen aus. Die ermittelten Ergebnisse werden im Formularbereich Ergebnisse Tageszinsrechnung ausgegeben.

Wurde eine Tageszinsrechnung durchgeführt, so bedienen Sie die Schaltfläche Darstellen um sich die Zusammenhänge grafisch zu veranschaulichen.
 

Allgemeines

 
Durch die Bedienung der Schaltfläche Löschen können alle Eingaben gelöscht werden.

Nach einer Bedienung der Schaltfläche Schließen kehren Sie wieder zum Hauptformular des Unterprogramms zurück.
 

Diagramme

 
Ausgegebene Diagramme können per Mausbedienung gezoomt werden.

Zoomen (Koordinatenwertebereich verkleinern)

Klicken Sie mit der linken Maustaste in den Darstellungsbereich des Diagramms und ziehen Sie unter Festhalten der Taste ein Rechteck auf (von links nach rechts und von oben nach unten). Nach dem Loslassen der Maustaste wird der umrandete Bereich auf den Gesamtdarstellungsbereich vergrößert.

Urzustand

Möchten Sie den Koordinatenwertebereich wieder in den Urzustand versetzen, so klicken Sie mit der linken Maustaste in den Darstellungsbereich des Diagramms und ziehen unter Festhalten der Taste ein Rechteck auf (von rechts nach links und von unten nach oben). Nach dem Loslassen der Maustaste wird der ursprüngliche Gesamtdarstellungsbereich wiederhergestellt.
 

 

Über den Menübefehl Datei - Ergebnisse exportieren besteht die Möglichkeit, die Ergebnisse in Tabellenform zu exportieren. Es stehen zur Verfügung:

 

Export in eine Excel-Tabelle im *.xls-Format (vertikale Anordnung)

Export in eine Excel-Tabelle im *.xls-Format (horizontale Anordnung)

Export in eine Text-Datei im *.txt-Format

Export in ein Word-Dokument im *.doc-Format in Tabellenform

Export in eine HTML-Seite im *.html-Format in Tabellenform

 

Achten Sie darauf, dass das entsprechende Programm (Word oder Excel) nicht geöffnet ist, während Sie diese Art von Datenexport durchführen, ansonsten erhalten Sie eine entsprechende Fehlermeldung.

 

Über den Menüpunkt Datei - Ergebnisse in Zwischenablage kopieren können die Ergebnisse in Tabellenform in die Zwischenablage kopiert werden. Nach dem Öffnen der entsprechenden Anwendung und einer Wahl des dortigen Befehls Einfügen bzw. der Bedienung der Tastenkombination Strg-V werden die Daten in der Anwendung abgelegt.
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema.

Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet der Mathematik, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe - Leistungskurs (LK).
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.

  

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

Weitere Themenbereiche

Jahreszinsrechnung

Annuitätentilgung

Zinseszinsrechnung grafisch
 

Beispiele

 
Beispiel 1 - Zinsrechnung:

Ein Kredit von 10000 EUR soll binnen eines Zeitraumes von 10 Jahren, bei einem festen Jahreszinssatz von 10% nachschüssig abbezahlt werden. Nach Eingabe der entsprechenden Werte in die Felder Kapital (10000), Zinssatz (10) und Jahre (10) sowie Rate (0) im Registerblatt Zinsrechnung, ermittelt das Programm nach einer Bedienung der Schaltfläche Berechnen:

Die nachschüssige Tilgungsrate beträgt 1627,45 €. Würde der Kredit vorschüssig abbezahlt werden, so beträge die Rate 1479,50 €. Für den anfänglichen Jahreszins wird ein Betrag von 1000 € ausgegeben.

Beispiel 2 - (Einfache) Zinsrechnung:

Ein eingezahlter Betrag von 1000 EUR wird jährlich um 100 EUR durch Zuzahlung vorschüssig erhöht. Ein stetiger Zinssatz von 6% wird gewährleistet. Nach 10 Jahren wurde daher ein Gesamtbetrag von 2000 EUR eingezahlt.

Werden die entsprechenden Werte in die Felder Kapital (1000), Zinssatz (6), Jahre (10) sowie Rate (100) im Registerblatt Zinsrechnung eingegeben, so gibt das Programm nach einer Bedienung der Schaltfläche Berechnen die jahresbezogenen Tabellenwerte aus.

Wie aus Spalte Kapital + Rate unter Eintrag Jahr 10 zu entnehmen ist, beträgt die verzinste Kapitalsumme nach 10 Jahren 3188,01 €.

Beispiel 3 - Jahreszinsrechnung:

Ein Guthaben von 2500 € wird über ein Jahr zu einem Zinssatz von 4 % angelegt. Wie viel Zinsen fallen für diesen Zeitraum an?

Nach einer Wahl des Registerblatts Jahres- und Tageszinsrechnung, der Eingabe der Werte in die Felder Kapital (2500) und Zinssatz (4) im Formularbereich Jahreszinsrechnung sowie einer Bedienung der Schaltfläche Berechnen ermittelt das Programm:

Der Zins für den Zeitraum eines Jahres beträgt 100 €. Der Kapitalendwert beträgt somit 2600 €.

Beispiel 4 - Tageszinsrechnung:

Ein Guthaben von 5000 Euro wird für 200 Tage zu einem Zinssatz von 7 Prozent festgelegt. Wie viel Zinsen fallen für diesen Zeitraum an?

Nach einer Wahl des Registerblatts Jahres- und Tageszinsrechnung, der Eingabe der Werte in die Felder Kapital (5000), Zinssatz (7), Zeitraum (200) im Formularbereich Tageszinsrechnung und einer Bedienung der Schaltfläche Berechnen gibt das Programm folgende Ergebnisse aus:

Der Zins für den Zeitraum von 200 Tagen beträgt 194,44 €. Der Zins pro Tag (über diesen Zeitraum) beträgt 0,972 €.
 

 

Beispiel 1


Beispiel 2


Beispiel 3
    

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
    

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Zinsrechnung sowie unter Wikipedia - Effektiver Jahreszins zu finden.
 

 

Zahlenstrahl - Römische Zahlen - Schriftliche Addition - Schriftliche Subtraktion - Schriftliche Multiplikation - Schriftliche Division - Schriftliche Potenzierung - Aussagenlogik - Zahltypumwandlung - Zinseszinsrechnung grafisch - Annuitätentilgung - Jahreszinsrechnung - Physikalische Größen - Materialkonstanten - Fachbegriffe Deutsch - Englisch - Mandelbrot- und Juliamengen - Zusammenhänge Mandelbrot-Juliamengen - Sierpinski-Dreieck - Koch-Kurve - Pythagoras-Baum - Feigenbaum-Diagramm - Lindenmayer-System - Lindenmayer-System II - Logistische Gleichung I - Logistische Gleichung II - Diagramme - Tortendiagramm - Kryptografie - Raumgittermodelle (3D) - Paare geordnet - Kalender - Rechnen mit selbstdefinierten Formeln - Zeichenprogramm - Tangram - Tetris - Spiel 15 - Türme von Hanoi - Dame - Schach

 

MathProf 5.0 - Unterprogramm Jahreszinsrechnung

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

  

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---