MathProf - Zinseszinsrechnung - Zinseszins - Rentenrechnung - Rente

Fachthema: Zinseszins - Rente
MathProf - Software für interaktive Mathematik für die Realschule, das Berufskolleg, das Gymnasium und das Studium zum Lösen verschiedenster Aufgaben sowie zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen.

Online-Hilfe
für das Modul zur grafischen Analyse der Zusammenhänge bei
der Durchführung von Zinseszinsrechnungen unter dem Einfluss vom Zinsfaktor.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Zinseszins - Zins und Zinseszins - Zinseszinsformel - Zinseszinsrechnung - Zinseszinsen - Zinsfaktor - Zinseszinsrechner - Jahre - Jährlich - Zinseszinsrechnungen - Kapital - Geld - Dollar - Euro - Formel - Erklärung - Einfach erklärt - Bedeutung - Was bedeutet - Was - Wie - Weshalb - Warum - Welche - Welcher - Welches - Wodurch - Beschreibung - Herleitung - Beweis - Definition - Zinsabschnitt - Zinsformel - Summenformel - Geometrische Summenformel - Grafik - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Einführung - Abituraufgaben - Abiturvorbereitung - Ergebnis - Abitur - Abi - Leistungskurs - LK - Begriff - Begriffe - Mathe - Mathematik - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Darstellen - Darstellung - Finanzrechner - Finanzen - Berechnung - Endkapital - Grundkapital - Zeitrente - Rente - Rentenrechnung - Raten - Zahlung - Grundlagen - Zahlungsperiode - Barwert - Endwert - Rentenzahlung - Rentenberechnung - Rentenhöhe - Rentenendwert - Rentenendwertfaktor - Aufzinsung - Abzinsung - Aufzinsungsfaktor - Abzinsungsfaktor - Aufzinsen - Abzinsen - Ratenhöhe - Berechnen - Darstellen - Rechner - Grafisch - Plotter - Graph - Zinsguthaben - Kapitalendwert |
Zinseszinsrechnung grafisch - Zinseszins - Rentenrechnung
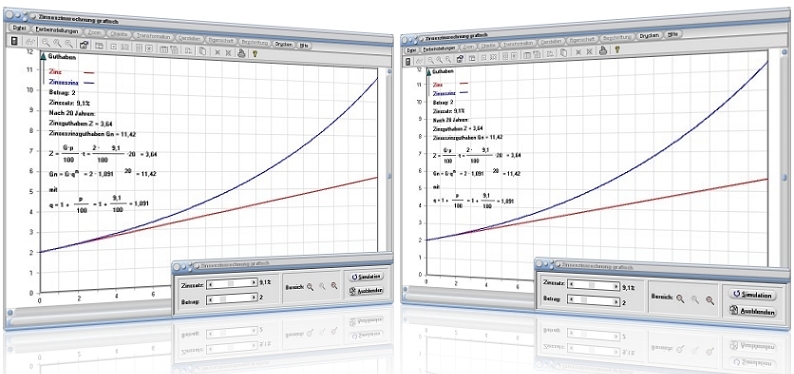
Modul Zinseszinsrechnung grafisch
Das kleine Programmmodul [Sonstiges] - Zinseszinsrechnung grafisch stellt den Zuwachs eines Guthabens in Abhängigkeit von einem Zinssatz grafisch dar.

Zinseszins entsteht, wenn ein Betrag auf ein Konto eingezahlt wird, eine Verzinsung des Guthabens am Ende eines Jahres erfolgt, der Betrag samt Zins auf diesem Konto belassen wird und im darauffolgenden Jahr (den darauffolgenden Jahren) eine weitere Verzinsung des Guthabens erfolgt. (Es wird der ursprünglich einbezahlte Betrag zzgl. dem bislang enthaltenen Zins verzinst)
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Grafische Darstellung
In diesem Unterprogramm können Sie einfache Untersuchungen zum Fachthema Zinseszinsrechnung durchführen.
Mathematische Zusammenhänge seien nachfolgend kurz aufgeführt:
Z = G·P/100·t
Gn = G·qn
mit
q = 1 + p/100
Z: Zinsen
Gn: Guthaben nach n Jahren
p: Jahreszinssatz in %
G : Guthaben (Anfangskapitalwert)
t: Zeit in Jahren
q: Zinsfaktor
Um sich diese Sachverhalte grafisch zu verdeutlichen, legen Sie mit den auf dem Bedienformular vorhandenen Schiebereglern Zinssatz und Betrag zunächst den Zinssatz in % und den zu verzinsenden Betrag fest.
Den Darstellungs- (und Berechnungsbereich) legen Sie durch die Ausführung von Mausklicks auf die entsprechenden Symbolschaltflächen im Formularbereich Bereich fest. Bei jeder Änderung eines Parameters oder des Darstellungsbereichs werden die Berechnungsergebnisse und die grafische Darstellung aktualisiert.
Um Zusammenhänge mit Hilfe von Simulationen zu analysieren, bedienen Sie die Schaltfläche Simulation. Vor dem Start einer Simulation wird Ihnen ein Formular zur Verfügung gestellt, auf welchem Sie die zu simulierende Größe durch eine Aktivierung des entsprechenden Kontrollschalters festlegen. Hierauf können Sie ggf. den Wert für die zu verwendende Verzögerung einstellen. Bestätigen Sie mit Ok. Beendet werden kann die Ausführung einer derartigen Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.
Zinseszinsrechnung - Formeln - Zinseszinsformel
Hinsichtlich der Berechnung von Zinseszinsen gilt allgemein:
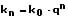
mit
q = 1 + p/100
Die folgende Formel wird als Zinseszinsformel bezeichnet.
kn = k0·(1 + p/100)n
Beispiel zur Berechnung des Zinseszins mit der Zinseszinsformel:
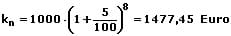
Nachfolgend sind Formeln zu weiteren Berechnungen zu diesem Fachthema aufgeführt.
Berechnung des Zinsfaktors:
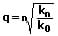
Berechnung des Zinssatzes:
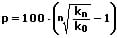
Berechnung von Zinsabschnitten:
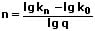
mit:
k0: Grundkapital
kn: Endkapital
p: Zinssatz
q: Zinsfaktor
Rentenrechnung: Bei der Rentenrechnung handelt es sich um ein klassisches Verfahren der Finanzmathematik. Hierbei erfolgt die Berechnung der Raten, mit denen ein zuvor angespartes Kapital in regelmäßigen Zeitabständen sowie in konstanter Höhe ausbezahlt wird.
Zeitrente: Eine Zeitrente ist eine Folge von Zahlungen, welche an festgelegten Zeitpunkten über eine bestimmte Anzahl von Jahren erfolgt. Als Raten der Zeitrente werden die einzelnen in gleichen Zeitabständen zu verrichtenden Zahlungen bezeichnet.
Barwert: Der Barwert einer Rente ist der Betrag aller Raten, der zu Beginn der Laufzeit zu zahlen ist, wenn der Endwert der Rente durch eine einmalige Zahlung abzulösen ist. Er ist ein Maß für den Wert, dem eine zukünftige Zahlung gegenwärtig entspricht. Der Barwert errechnet sich wie folgt:

mit Abzinsungsfaktor:

Aufzinsungsfaktor: q = 1+i
Der Abzinsungsfaktor dient dazu, einen Geldbetrag anhand eines Zinssatzes auf einen in der Vergangenheit liegenden Zeitpunkt zurückzurechnen. Dieser kann ebenfalls für einen zukünftig anfallenden Geldbetrag auf den heutigen Zeitpunkt zurückgerechnet werden.
Endwert - Rentenendwert: Der Endwert einer Rente (der Rentenendwert) ist der Wert aller bis zur Auszahlung der Rente entrichteter Raten, zu Ende der Laufzeit. Er ist ein Maß für den Wert, dem eine jetzige Zahlung zukünftig entspricht. Für den Endwert gilt:

Vorschüssig: Als vorschüssig werden Zahlungen von Raten bezeichnet, welche zu Anfang einer Zahlungsperiode geleistet werden (z.B. zu Anfang eines Monats).
Nachschüssig: Als nachschüssig werden Zahlungen von Raten bezeichnet, welche zu Ende einer Zahlungsperiode geleistet werden (z.B. zu Ende eines Monats).
Barwert und Endwert bei einer Rentenzahlung: Der Teil der Gleichung (nachfolgend rechts ausgegeben, z.B. ((1+n)n -1)/i ) der die Ratenhöhe sowie den jährlichen Zinssatz beinhaltet, wird als Rentenendwertfaktor bezeichnet.
Barwert einer Rente bei vorschüssiger Ratenzahlung:

Endwert einer Rente bei vorschüssiger Ratenzahlung:

Barwert einer Rente bei nachschüssiger Ratenzahlung:

Endwert einer Rente bei nachschüssiger Ratenzahlung:

mit:
R: Ratenhöhe
n: Ratenanzahl
i: Jährlicher Zinssatz
K0: Heutiger Barwert
Kn: Endwert in n Jahren
Als Aufzinsung wird die Berechnung bezeichnet, mit der ermittelt wird, welche Höhe ein Geldbetrag in Zukunft im Vergleich zum aktuellen Zeitpunkt besitzen könnte. Als Abzinsung wird die Berechnung bezeichnet, mit der ermittelt wird, was eine Zahlung zu einem früheren Zeitpunkt wert gewesen wäre.
Die geometrische Summenformel kann bei der Berechnung von Zinserträgen eingesetzt werden. Sie ist wie folgt definiert:

Beispiel:
Werden über einen Zeitraum von 5 Jahren jährlich 1000 Euro gespart und über diesen hinweg mit 5% verzinst, so ergibt sich für den Betrag des Ersparten über diesen Zeitraum:

Bedienformular

Durch die Ausführung eines Mausklicks auf das entsprechende Lupensymbol verkleinern oder vergrößern Sie den Darstellungsbereich.
Allgemein
Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben.
Weitere Themenbereiche
Beispiel
Legen Sie mit den zur Verfügung stehenden Schiebereglern einen Zinssatz von 5%, sowie einen Anfangskapitalwert von 6 EUR fest (mittlere Symbolschaltfläche im Formularbereich Bereich deaktiviert), so werden folgende Berechnungsschritte ausgeführt:
Zinsguthaben Z:
Z = G·P/100·t = 6·5/100·20 = 6 EUR
Guthaben Gn nach n = 20 Jahren:
Gn = G·qn = 6·1,0520 = 15,92 EUR
mit
q = 1+p/100 = 1 + 5/100 = 1,05
Hieraus kann entnommen werden:
Wird ein Kapital von 6 EUR über 20 Jahre hinweg mit einem stetigen Zinssatz von 5% verzinst, so beträgt der Kapitalendwert hiernach 15,92 EUR.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet der Mathematik, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.

Grafische Darstellung - Beispiel 1

Grafische Darstellung - Beispiel 2
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Zinseszins zu finden.
Zahlenstrahl - Römische Zahlen - Schriftliche Addition - Schriftliche Subtraktion - Schriftliche Multiplikation - Schriftliche Division - Schriftliche Potenzierung - Aussagenlogik - Zahltypumwandlung - Zinsrechnung - Annuitätentilgung - Jahreszinsrechnung - Physikalische Größen - Materialkonstanten - Fachbegriffe Deutsch - Englisch - Mandelbrot- und Juliamengen - Zusammenhänge Mandelbrot-Juliamengen - Sierpinski-Dreieck - Koch-Kurve - Pythagoras-Baum - Feigenbaum-Diagramm - Lindenmayer-System - Lindenmayer-System II - Logistische Gleichung I - Logistische Gleichung II - Diagramme - Tortendiagramm - Kryptografie - Raumgittermodelle (3D) - Paare geordnet - Kalender - Rechnen mit selbstdefinierten Formeln - Zeichenprogramm - Tangram - Tetris - Spiel 15 - Türme von Hanoi - Dame - Schach
MathProf 5.0 - Unterprogramm Annuitätentilgung

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















