MathProf - Stellenwerttafel - Hundertertafel - Magische Quadrate - Rechenbaum

Fachthemen: Zahlenstrahl - Zahlen - Rechnen
MathProf - Arithmetik - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für Schüler, Abiturienten, Studenten, Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Darstellung der prinzipiellen
Anordnung natürlicher Zahlen am Zahlenstrahl.
Auf dieser Seite sind zudem Informationen zu weiteren relevanten Fachthemen zu finden.
Hierzu zählen unter anderem die Themengebiete Nachbarzahlen, Stellenwerttafel, Zahlenreihen, Zahlenpyramiden, Zahlendreiecke, Zahlenmauern, Rechendreieck, Rechenbaum, Zahlenhaus, Rechenhaus, Hundertertafel und Rechentabelle sowie viele andere Informationen zu verschiedenen Bereichen der in der Grundschule behandelten Mathematik.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Zahlenstrahl - Zahlen - Strahl - Zahlengerade - Zahlen ordnen - Zahlen vergleichen - Dezimalzahlen vergleichen - Rechnen - Rechnen bis 1000 - Rechnen bis 100 - Rechnen bis 10 - Bis - 0 - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 11 - 12 - 13 - 14 - 15 - 16 - 17 - 18 - 19 - 20 - 30 - 40 - 50 - 60 - 70 - 80 - 90 - 100 - 1000 - 10000 - 100000 - 1000000 - Wie viele Nullen hat - Nullen - Mit Nullen - Ganze Zahlen ordnen - Mathe - Mathematik - Mathematische Grundlagen - Übersicht - Bestimmen - Ordnen - Anordnen - Ziffer - Zahl - Ziffern - Gültige Ziffern - Geltende Ziffern - Signifikante Stellen - Stellen - Stelle - Stellenwert - Stellenwerte - Zählen - Zahlbeziehungen - Stellenwerttafeln - Stellentafel - Minuszahlen - Fehlende Zahl - Fehlende Zahlen - Stellenwerttafel - Stellenwertschreibweise - Stellenwerttabelle - Rechenweg - Zahlworte - Zehnerzahlen - Hunderterzahlen - Tausenderzahlen - Mehrstellige Zahl - Mehrstellige Zahlen - Negative Zahlen - Dekadische Einheiten - Dezimale Einheiten - Dekadisch - Dezimal - Vielfachenmenge - Dekadisches Zahlensystem - Zahldarstellung - Grundlagen - Darstellen - Darstellung - Zahlendarstellung - Aufgabe - Aufgaben - Begriff - Begriffe - Vorgänger - Nachfolger - Mitte von zwei Zahlen - Mitte zweier Zahlen - Zahlenlehre - Mathe - Mathematik - Klasse 1 - Klasse 2 - Klasse 3 - Klasse 4 - 1. Klasse - 2. Klasse - 3. Klasse - 4. Klasse - Erste Klasse - Zweite Klasse - Dritte Klasse - Vierte Klasse - Grundschule - Kopfgeometrie - Bedeutung - Was bedeutet - Erklärung - Einfach erklärt - Einführung - Beschreibung - Definition - Was - Wie - Weshalb - Was ist - Wie viel - Was sind - Wie viele - Wieviel - Wieviele - Wie viele Nullen - Wie berechnet man - Welche - Welcher - Welches - Wodurch - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Matheaufgaben - Herleitung - Beweis - Üben - Übungen - Übungsaufgaben - Bestimmen - Berechnen - Eins - Einer - Zehner - Hunderter - Tausender - Zehntausender - Hunderttausender - Nachbarzehner - Nachbarhunderter - Nachbartausender - Zehn - Hundert - Tausend - Einhundert - Eintausend - Zehntausend - Einhunderttausend - Eine Million - Milliarde - Billion - Zehntel - Hundertstel - Tausendstel - Zehntausendstel - Hunderttausendstel - Millionstel - Milliardstel - Tausenderstelle - Hunderterstelle - Einerstelle - Zehnerstelle - Zehnerübergang - Einstellige Zahlen - Zweistellige Zahlen - Dreistellige Zahlen - Vierstellige Zahlen - Fünfstellige Zahlen - Sechsstellige Zahlen - Einstellige Zahl - Zweistellige Zahl - Dreistellige Zahl - Vierstellige Zahl - Fünfstellige Zahl - Sechsstellige Zahl - 1 stellige Zahl - 2 stellige Zahl - 3 stellige Zahl - 4 stellige Zahl - 5 stellige Zahl - 6 stellige Zahl - Einstellig - Zweistellig - Dreistellig - Vierstellig - Fünfstellig - Sechsstellig - ZR 10 - ZR 100 - ZR 1000 - ZR 10000 - Zahlenpyramide - Zahlenmauer - Zahlenpyramiden - Zahlenmauern - Rechenmauer - Rechenmauern - Rechenpyramide - Rechenpyramiden - Zahlendreieck - Zahlendreiecke - Rechendreieck - Rechendreiecke - Mauer - Mauern - Reihen - Malreihe - Malreihen - Zahlentürme - Zahlenturm - Zahlenreihe - Zahlenreihen - Zweierreihe - Dreierreihe - Viererreihe - Fünferreihe - Sechserreihe - Siebenerreihe - Achterreihe - Neunerreihe - Zehnerreihe - Verliebte Zahlen - Partnerzahlen - Rechenbaum - Rechenbäume - Termbaum - Gliederungsbaum - Zahlenhaus - Rechenhaus - Zahlenhäuser - Rechenhäuser - Hundertertafel - Hundertertafeln - Hunderterfeld - Dreieckszahl - Dreieckszahlen - Spiegelzahl - Spiegelzahlen - Umkehrzahl - Umkehrzahlen - Zahlenquadrat - Zahlenquadrate - Magisches Quadrat - Magische Quadrate - Zauberquadrate - Zauberquadrat - 3x3 - 4x4 - 5x5 - Rechentabelle - Rechentafel - Rechentabellen - Rechentafeln - Zahlenraum - Zahlenräume - Ergänzung - Ergänzen - Einheitsstrecke - Zahlenwort - Zahlworte - Zahlwörter - Numeralien - Numerale - Kardinalzahlen - Grundzahlen - Bruchzahlen - Ordinalzahlen - Fermi-Fragen - Fermi-Aufgaben - Fermi-Problem - Fermi - Frage - Aufgabe - Problem - Rechenaufgabe - Kettenaufgabe - Rechenaufgaben - Kettenaufgaben - Rechenschlange - Rechenschlangen - Rechenkette - Rechenketten - Tauschaufgaben - Umkehraufgaben - Tauschaufgabe - Umkehraufgabe - Platzhalteraufgaben - Ergänzungsaufgaben - Lückenaufgaben - Kapitänsaufgaben - Zahlenfeld - Punktebild - Punktefeld - Punktebilder - Punktefelder - Rechenoperationen - Rechenstrategien - Wie viele Nullen hat eine Million - Wie viele Nullen hat eine Milliarde - Wie viele Nullen hat eine Billion - Wie viele Nullen hat eine Billiarde - Wie viele Nullen hat eine Trillion - Wie viele Nullen hat eine Trilliarde - Trillion - Trilliarde - Quadrillion - Quadrilliarde - Quintillion - Quintilliarde - Sextillion - Sextilliarde - Septillion - Septilliarde - Oktillion - Oktilliarde - Nonillion - Nonilliarde - Dezillion - Dezilliarde - Zentillion - Zahlennamen - Namen - Ziffernfolge |
Zahlenstrahl - Stellenwerttafel - Zahlenreihe - Zahlenpyramide - Zahlendreieck - Rechendreieck - Stellenwerte - Rechenbaum - Zahlenhaus - Rechenhaus - Hundertertafel - Zauberquadrate - Magische Quadrate - Zahlenquadrate

Modul Zahlenstrahl
Das kleine Unterprogramm [Sonstiges] - [Arithmetik] - Zahlenstrahl ermöglicht durch das Tauschen die prinzipielle Anordnung natürlicher Zahlen, gemäß derer Position auf dem Zahlenstrahl.

Ein Zahlenstrahl (eine Zahlengerade) besteht aus einer horizontal angeordneten Linie, auf welcher ganze Zahlen entsprechend ihrer Größe positioniert werden. Ein Zahlenstrahl ist eine Halbgerade und weist lediglich positive Zahlen auf. Sie dient der Veranschaulichung der natürlichen Zahlen.
Eine Zahlengerade hingegen ist eine Gerade und kann auch negative Zahlen beinhalten. Die Abstände zwischen je zwei angeordneten Zahlen sind stets gleich groß. Je weiter rechts sich eine Zahl auf dem Strahl befindet, desto größer ist sie.
Der Abstand zwischen den Strichen des Zahlenstrahls oder der Zahlengerade wird als Einheitsstrecke bezeichnet.
Ganze Zahlen ordnen: Beim Ordnen von Zahlen von klein nach groß werden (von links nach rechts) zuerst die kleinen Zahlen und hierauf die größeren Zahlen ihrer Größe entsprechend aufsteigend positioniert (aufsteigend sortiert). Bei der Durchführung des absteigenden Sortierens erfolgt diese Vorgehensweise in umgekehrter Richtung. Es erfolgt das Ordnen von groß nach klein.
Als Zahlenraum wird eine auf eine bestimmte Weise begrenzte oder definierte Menge von Zahlen bezeichnet. Häufig zur Durchführung von Rechenaufgaben verwendete Zahlenräume sind die Zahlenräume ZR 10, ZR 100, ZR 1000, ZR 10000 und ZR 100000. Als Zahldarstellung oder Zahlendarstellung wird das Format der Darstellung einer Zahl bezeichnet. Sie erfolgt häufig in Form einer Zahlschrift oder mit Hilfe von Zahlwörten oder Zahlennamen.
In diesem kleinen Modul besteht die Möglichkeit die Position dreier Zahlen auf dem Zahlenstrahl verändern und diese korrekt anzuordnen.
Klicken Sie mit der linken Maustaste auf eines der drei obig angeordneten Zahlensymbole und ziehen Sie dieses an deren korrekte Position im Zahlenstrahl. Befindet sich die Zahl innerhalb des gewählten Rechtecks, so muss die Maustaste losgelassen werden. Wiederholen Sie dies für die beiden anderen Zahlen. Das Programm zeigt daraufhin an, ob die Anordnung bzgl. derer Position auf dem Zahlenstrahl in richtiger Reihenfolge erfolgte, oder nicht.
Wiederholen können Sie dies mit den gleichen Zahlenwerten, indem Sie die Schaltfläche Wiederholen drücken. Soll vom Programm eine neue Zahlenkombination erzeugt werden, so ist die Schaltfläche Neue Aufgabe zu bedienen. Durch einen Klick auf die Schaltfläche Beenden schließen Sie dieses Unterprogramm.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle

Beispiel 1

Beispiel 2

Beispiel 3
Zahlen werden unter der Verwendung von Ziffern geschrieben. Um sämtliche (unendliche viele) Zahlen zu bilden genügen die zehn Ziffern 0, 1, 2, 3, 4, 5, 6, 7, 8 und 9. Außer dem Wert der Ziffer selbst ist ihre Position im Stellenwertwertsystem ausschlaggebend. Der Wert einer Ziffer erhöht sich bei jeder Position von rechts nach links um das Zehnfache. Zahlen werden als Summen von Stellenwerten gebildet.
Das häufig verwendete Zehnersystem wird auch als dekadisches Zahlensystem oder Dezimalsystem bezeichnet, denn die Worte dekadisch oder dezimal besitzen die Bedeutung: zehnteilig bzw. auf die Zahl 10 bezogen. Dezimale Einheiten werden in diesem Stellenwertsystem dekadische Einheiten genannt. Zur Darstellung der Zahlen in diesem System mittels einer Stellenwerttafel werden Bezeichnungskürzel für dekadische und dezimale Einheiten verwendet. Diese sind nachfolgend aufgeführt.
Als Kopfgeometrie wird das Lösen geometrischer Aufgaben im Kopf und somit ohne Hilfsmittel bezeichnet. Aufgaben der Kopfgeometrie umfassen meist ein visuelles Handeln in der Vorstellung auf der Basis geometrischer Grundbegriffe.
Dekadische Einheiten und ihre Kürzel (Zahlworte):
Diese Tabelle zeigt dekadische Einheiten und deren Kürzel sowie deren Anzahl an Nullen:
| Dekadische Einheit | Zahlwort | Kürzel | Nullen |
| 1 | Eins | E | 0 |
| 10 | Zehn | Z | 1 |
| 100 | Hundert | H | 2 |
| 1 000 | Tausend | Z | 3 |
| 10 000 | Zehntausend | ZT | 4 |
| 100 000 | Hunderttausend | HT | 5 |
| 1 000 000 | Million | M | 6 |
| 10 000 000 | Zehn Millionen | ZM | 7 |
| 100 000 000 | Hundert Millionen | HM | 8 |
| 1 000 000 000 | Milliarde | Md | 9 |
| 10 000 000 000 | Zehn Milliarden | ZMd | 10 |
| 100 000 000 000 | Hundert Milliarden | HMd | 11 |
| 1 000 000 000 000 | Billion | B | 12 |
Zehnerzahlen: Eine Zahl wird als Zehnerzahl bezeichnet, wenn ihre letzte Ziffer eine 0 ist.
Hunderterzahlen: Eine Zahl wird als Hunderterzahl bezeichnet, wenn ihre letzten beiden Ziffern 0 sind.
Tausenderzahlen: Eine Zahl wird als Tausenderzahl bezeichnet, wenn ihre letzten drei Ziffern 0 sind.
Wie viele Nullen hat eine Million?
Eine Million besitzt 6 Nullen
Wie viele Nullen hat eine Millarde?
Eine Milliarde besitzt 9 Nullen
Wie viele Nullen hat eine Billion?
Eine Billion besitzt 12 Nullen
Wie viele Nullen hat eine Billiarde?
Eine Billiarde besitzt 15 Nullen
Wie viele Nullen hat eine Trillion?
Eine Trillion besitzt 18 Nullen
Dezimale Einheiten und ihre Kürzel (Zahlworte):
Diese Tabelle zeigt dezimale Einheiten und deren Kürzel:
| 0,1 | Zehntel | z |
| 0,01 | Hundertstel | h |
| 0,001 | Tausendstel | t |
| 0,0 001 | Zehntausendstel | zt |
| 0,00 001 | Hunderttausendstel | ht |
| 0,000 001 | Millionstel | m |
| 0,0 000 001 | Zehnmillionstel | zm |
| 0,00 000 001 | Hundertmillionstel | hm |
| 0,000 000 001 | Milliardstel | md |
Die nachfolgend gezeigte Tabelle beinhaltet Ziffernfolgen sowie deren Zahlenname:
| Ziffernfolge | Zahlenname |
| 1 | Eins |
| 10 | Zehn |
| 100 | Hundert |
| 1.000 | Tausend |
| 1.000.000 | Million |
| 1.000.000.000 | Milliarde |
| 1.000.000.000.000 | Billion |
| 1.000.000.000.000.000 | Billiarde |
| 1.000.000.000.000.000.000 | Trillion |
| 1.000.000.000.000.000.000.000 | Trilliarde |
| 1.000.000.000.000.000.000.000.000 | Quadrillion |
| 1.000.000.000.000.000.000.000.000.000 | Quadrilliarde |
| Ziffer 1 gefolgt von 30 Nullen | Quintillion |
| Ziffer 1 gefolgt von 33 Nullen | Quintilliarde |
| Ziffer 1 gefolgt von 36 Nullen | Sextillion |
| Ziffer 1 gefolgt von 39 Nullen | Sextilliarde |
| Ziffer 1 gefolgt von 42 Nullen | Septillion |
| Ziffer 1 gefolgt von 45 Nullen | Septilliarde |
| Ziffer 1 gefolgt von 48 Nullen | Oktillion |
| Ziffer 1 gefolgt von 51 Nullen | Oktilliarde |
| Ziffer 1 gefolgt von 54 Nullen | Nonillion |
| Ziffer 1 gefolgt von 57 Nullen | Nonilliarde |
| Ziffer 1 gefolgt von 60 Nullen | Dezillion |
| Ziffer 1 gefolgt von 63 Nullen | Dezilliarde |
| Ziffer 1 gefolgt von 66 Nullen | Undezillion |
| Ziffer 1 gefolgt von 69 Nullen | Undezilliarde |
| Ziffer 1 gefolgt von 72 Nullen | Duodezillion |
| Ziffer 1 gefolgt von 75 Nullen | Duodezilliarde |
| Ziffer 1 gefolgt von 78 Nullen | Tredezillion |
| Ziffer 1 gefolgt von 81 Nullen | Tredezilliarde |
| Ziffer 1 gefolgt von 84 Nullen | Quattuordezillion |
| Ziffer 1 gefolgt von 37 Nullen | Quattuordezilliarde |
| Ziffer 1 gefolgt von 90 Nullen | Quindezillion |
| Ziffer 1 gefolgt von 600 Nullen | Zentillion |
Nachbarzehner - Nachbarhunderter - Nachbartausender:
Zehner sind alle Zahlen, die ohne Rest durch 10 teilbar sind. Hunderter sind alle Zahlen, die ohne Rest durch 100 teilbar sind. Tausender sind alle Zahlen, die ohne Rest durch 1000 teilbar sind. Zehner sind Zahlen die mindestens eine 0 am Ende besitzen.
Zweistellige Zahlen besitzen Nachbarzehner. Dreistellige Zahlen besitzen Nachbarhunderter und vierstellige Zahlen besitzen Nachbartausender. Jede Zahl besitzt stets zwei Nachbarzehner. Als Nachbarzehner werden die Zahlen bezeichnet, welche ohne Rest durch 10 teilbar sind.
Der kleine Nachbarzehner ist kleiner als die entsprechende Zahl. Der größere Nachbarzehner ist größer als die entsprechende Zahl.
Beispiele zu ganzen Zahlen:
Die Nachbarzehner von 5 sind die Zahlen 0 und 10.
Die Nachbarzehner von 13 sind die Zahlen 10 und 20.
Die Nachbarzehner von 74 sind die Zahlen 70 und 80.
Beispiele zu Kommazahlen:
Die Nachbarzehner von 0,17 sind die Zahlen 0 und 10.
Die Nachbarzehner von 3,9 sind die Zahlen 10 und 20.
Die Nachbarzehner von 63,14 sind die Zahlen 70 und 80.
Beispiele zu negativen Zahlen:
Die Nachbarzehner von -4 sind die Zahlen -10 und 0.
Die Nachbarzehner von -38 sind die Zahlen -40 und -30.
Die Nachbarzehner von -83 sind die Zahlen -90 und -80.
Zehnerübergang:
Als Zehnerübergang wird beim Durchführen von Rechenaufgaben die bezeichnet, wenn das Berechnungsergebnis einer Aufgabe im nächsten (oder einem anderen) Zehner liegt. Beim Lösen der Aufgaben 9 + 2 = 11 oder 7 + 5 = 12 liegt beispielsweise in beiden Fällen ein Zehnerübergang vor.
Minuszahlen:
Als Minuszahlen werden negative Zahlen bezeichnet, die kleiner als Null sind.
Zahlworte (Numeralien):
Als Zahlwort (Numerale) wird eine Wortart bezeichnet, mit Hilfe derer die Menge, die Anzahl oder der Rang eines Dinges oder einer Sache beschreiben wird. Sie werden untergliedert in bestinmmte und unbestimmte Numeralien (Zahladjektive). Bestimmte Numeralien gliedern sich wie folgt in:
- Kardinalzahlen oder Grundzahlen (z.B: eins, zwei, drei)
- Bruchzahlen (z.B.: ein Drittel, ein Viertel, ein Sechstel)
- Ordinalzahlen (z.B.: erster, zweiter, dritter)
- Zahlwörter der Vervielfältigung (z.B.: doppelt, dreifach, zweimalig)
- Zahlworte einer Gattung (z.B.: einerlei, dreierlei, viererlei)
Zahlworte dieser Art geben Auskunft über eine genaue Anzahl.
Stelle und Stellenwert: Der Wert einer Zahl resultiert aus der Anordnung der Ziffern in einer Ziffernfolge. Als Stellen werden die Positionen einer Ziffer in dieser Anordnung bezeichnet. Jeder dieser Stellen wird ein Stellenwert zugewiesen, der einer Potenz der Basis entspricht. Die Stelle mit dem höchsten Stellenwert befindet sich hierbei ganz links, die Stelle mit dem niedrigsten Stellenwert hingegen ganz rechts. Im Dezimalsystem gilt für die Darstellung natürlicher Zahlen hinsichtlich derer Stellenwerte zum Beispiel:
Der Stellenwert der von rechts aus gesehenen ersten Stelle ist 100 = 1 (Einerstelle).
Der Stellenwert der von rechts aus gesehenen zweiten Stelle ist 101 = 10 (Zehnerstelle).
Der Stellenwert der von rechts aus gesehenen dritten Stelle ist 102 = 100 (Hunderterstelle).
Der Stellenwert der von rechts aus gesehenen vierten Stelle ist 103 = 1000 (Tausenderstelle).
usw.
Stellenwerttafeln: Eine Stellenwerttafel (Stellenwerttabelle oder Stellentafel) wird in der Grundschule eingesetzt um Zahlen in übersichtlicher Weise darzustellen. Hierbei erfolgt die Aufteilung einer Zahl in Einer, Zehner, Hunderter, Tausender usw. Sie ist dienlich zur Einordnung von Zahlen. Es wird zwischen folgenden Stellenwerten unterschieden: Einer, Zehner, Hunderter, Tausender, Zehntausender, Hunderttausender, Millionen, Zehnmillionen, Hundertmillionen, Milliarden, Zehnmilliarden, Hundertmilliarden, Billionen, usw.
Darstellung von Zahlen in Form von Stellenwerten:
Stellenwertschreibweise: Nachfolgend sind einige Beispiele zur Darstellung dekadischer Zahlen in der Stellenwerttafel für Einer, Zehner, Hunderter und Tausender aufgeführt.
Beispiel 1 - Zahl 7:
Die Zahl 7 besitzt lediglich eine Einerstelle, jedoch keine Zehnerstelle, keine Hunderterstelle, keine Tausenderstelle usw.
Ihre Darstellung in der Stellenwerttafel erfolgt daher wie folgt:
| T | H | Z | E |
| 7 |
Als Stellenwert geschrieben: 7E
Beispiel 2 - Zahl 59:
Die Zahl 59 besitzt eine Einerstelle, eine Zehnerstelle, jedoch keine Hunderterstelle, keine Tausenderstelle usw. Ihre Darstellung in der Stellenwerttafel erfolgt daher wie folgt:
| T | H | Z | E |
| 5 | 9 |
Als Stellenwert geschrieben: 5Z 9E
Beispiel 3 - Zahl 148:
Die Zahl 148 besitzt eine Einerstelle, eine Zehnerstelle, eine Hunderterstelle, jedoch keine Tausenderstelle usw. Ihre Darstellung in der Stellenwerttafel erfolgt daher wie folgt:
| T | H | Z | E |
| 1 | 4 | 8 |
Als Stellenwert geschrieben: 1H 4Z 8E
Beispiel 3 - Zahl 3169:
Die Zahl 3169 besitzt eine Einerstelle, eine Zehnerstelle, eine Hunderterstelle, eine Tausenderstelle, jedoch keine Zehntausenderstelle usw. Ihre Darstellung in der Stellenwerttafel erfolgt daher wie folgt:
| T | H | Z | E |
| 3 | 1 | 6 | 9 |
Als Stellenwert geschrieben: 3T 1H 6Z 9E
Beispiel 4 - Zahlen 1, 10, 100, 1 000, 10 000, 100 000, 1 000 000:
Die nachfolgend aufgeführte Tabelle zeigt die Darstellung der Zahlen 1, 10, 100, 1 000, 10 000, 100 000 sowie 1 000 000 in der Stellenwerttafel.
| M | HT | ZT | T | H | Z | E |
| 1 | ||||||
| 1 | 0 | |||||
| 1 | 0 | 0 | ||||
| 1 | 0 | 0 | 0 | |||
| 1 | 0 | 0 | 0 | 0 | ||
| 1 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Darstellung von Stellenwerten als Dezimalzahl:
Bei Anwendung der Summenschreibweise können Nullen weggelassen werden.
Ist die Zahl 7T 6H 4Z als Dezimalzahl auszugeben, so ergibt sich: 7640
Wird die Zahl 3HT 6T 4Z 3E als Dezimalzahl auszugeben, so ergibt sich: 306 043
Vorgänger - Nachfolger:
Die ganze Zahl, die sich vor einer betrachten Zahl befindet, wird als Vorgänger bezeichnet. Mit Nachfolger wird diejenige ganze Zahl benannt, welche sich nach einer betrachteten Zahl befindet.
Beispiele:
Der Vorgänger der Zahl 5 ist die Zahl 4. Der Nachgänger der Zahl 6 ist die Zahl 7.
Mitte zweier Zahlen:
Die Mitte zweier Zahlen (Mitte zwischen zwei Zahlen) ist diejenige Zahl, die den gleichen Abstand zu den beiden anderen Zahlen besitzt.
Beispiel:
Die Mitte der beiden Zahlen 3 und 9 ist die Zahl 6, da gilt:
3 + 9 = 12
und durch die anschliessende Division der Summe dieser beiden Zahlen ergibt sich, wie nachfolgend gezeigt die Zahl 6.
(3 + 9) / 2 = 12/ 2 = 6
Gültige Ziffern - Geltende Ziffern - Signifikante Stellen:
Als geltende Ziffern oder gültige Ziffern (signifikante Stellen) werden alle von der Zahl Null verschiedenen Ziffern bezeichnet. Alle Nullen, die sich als Endnullen oder Zwischennullen in einer Ziffer befinden gehören dazu. Eine Beachtung des Dezimalseparators (Kommas) ist hierbei nicht von Relevanz. Bei der Bestimmung gültiger (geltender) Ziffern werden die sich vor einer Ziffer befindenden Nullen nicht berücksichtigt. Es gilt:
- Die Erfassung erfolgt ab der ersten von Null verschiedenen Ziffer
- Die Erfassung erfolgt bis zur letzten Ziffer
- Die einer Ziffer vorangehenden Nullen werden nicht gezählt
Beispiele zu geltenden Ziffern:
1,3 besitzt 2 geltende Ziffern
0,13 besitzt 2 geltende Ziffern
0,013 besitzt 2 geltende Ziffern
0,0013 besitzt 2 geltende Ziffern
0,130 besitzt 3 geltende Ziffern
1300 besitzt 4 geltende Ziffern
1,000 besitzt 4 geltende Ziffern
Zahlen vergleichen: Um zwei (ganze) Zahlen miteinander zu vergleichen, werden sie gemäß ihrer Stellen (stellengerecht geordnet nach Zehnerstelle, Hunderterstelle, Tausenderstelle etc.) untereinander geschrieben. Hierauf können die entsprechenden Stellen dieser Zahlen miteinander verglichen werden.
Dezimalzahlen vergleichen: Zwei Dezimalzahlen kann man vergleichen, indem die natürlichen Zahlen betrachtet werden, die sich vor dem Komma befinden. Sind beide dieser Zahlen gleich groß, so werden deren Nachkommastellen von links ausgehend nach rechts betrachtet verglichen. Befindet sich nun an einer bestimmten Stelle dieser beiden Zahlen eine größere Ziffer, so stellt diese Zahl die auch die größerer Dezimalzahl dar.
Eine einstellige Zahl besteht aus lediglich einer Ziffer. Eine mehrstellige Zahl besitzt hingegen mehrere Ziffern.
Einstellige Zahlen (1-stellige Zahlen): Eine einstellige Zahl besteht aus einer Ziffer. Alle ganzen Zahlen zwischen 0 und 9 sind somit einstellig. Beispiel: 5
Zweistellige Zahlen (2-stellige Zahlen): Eine zweistellige Zahl setzt sich aus zwei Ziffern zusammen. Deren Einer befinden sich an zweiter und ihre Zehner sind an erster Stelle. Alle ganzen Zahlen zwischen 10 und 99 sind somit zweistellig. Beispiel: 28
Dreistellige Zahlen (3-stellige Zahlen): Eine dreistellige Zahl setzt sich aus drei Ziffern zusammen. Deren Einer befinden sich an dritter, ihre Zehner sind an zweiter und ihre Hunderter befinden sich an erster Stelle. Alle ganzen Zahlen zwischen 100 und 999 sind somit dreistellig. Beispiel: 759
Vierstellige Zahlen (4-stellige Zahlen): Eine vierstellige Zahl setzt sich aus vier Ziffern zusammen. Deren Tausender befinden sich an erster, ihre Hunderter an zweiter, ihre Zehner an dritter und ihre Einer an vierter Stelle. Alle ganzen Zahlen zwischen 1000 und 9999 sind somit vierstellig. Beispiel: 4098
Fünfstellige Zahlen (5-stellige Zahlen): Eine fünfstellige Zahl setzt sich aus fünf Ziffern zusammen. Deren Einer befinden sich an fünfter, ihre Zehner an vierter, ihre Hunderter an dritter, ihre Tausender an zweiter und ihre Zehntausender an erster Stelle. Alle ganzen Zahlen zwischen 10000 und 99999 sind somit fünfstellig. Beispiel: 30975
Sechsstellige Zahlen (6-stellige Zahlen): Eine sechsstellige Zahl setzt sich aus sechs Ziffern zusammen. Deren Einer befinden sich an sechster, ihre Zehner an fünfter, ihre Hunderter an vierter, ihre Tausender an dritter, ihre Zehntausender an zweiter und ihre Huderttausender erster Stelle. Alle ganzen Zahlen zwischen 100000 und 999999 sind somit sechsstellig. Beispiel: 780994
Weitere Besipiele für ein- und mehrstellige Zahlen sind nachfolgend aufgeführt.

Mit den Begriffen Zahlenpyramiden, Zahlendreiecke, Rechenmauern, Rechenpyramiden oder Zahlentürme werden didaktische Mittel benannt, bei denen Zahlen in pyramidenförmig angeordneten Feldern auf derartige Weise einzutragen sind, damit diese jeweils der Summe der beiden sich schräg darunter befindenden Zahlen entsprechen.
Zahlenmauern besitzen eine pyramidenförmige Struktur und sind dienlich die Grundlagen der Addition zu erlernen. Jede ihrer Zellen ist gleich der Summe der beiden darunter liegenden. In jedem ihrer Felder steht die Summe der beiden darunter stehenden Zahlen. Eine Zahlenmauer wird auch als Zahlendreieck, Zahlenpyramide, Rechenmauer, Rechenpyramide oder Zahlenturm bezeichnet.
Zur Lösung der Aufgaben mit Zahlenpyramiden sind Zahlen in die pyramidenförmig angeordneten Felder derart einzusetzen, damit diese stets der Summe der Zahlen der schräg darunter angeordneten Felder entsprechen. Vorgegeben wird die hierbei eine bestimmte Anzahl von Grundsteinen (Felder mit Zahlen) und die noch fehlenden Zahlen sind mit Hilfe einfacher Additionen zu ermitteln und in leere Felder einzutragen.
Nachfolgend gezeigt sind an den Beispielen 3- bis 6-reihiger Zahlenmauern (Rechenmauern) der Aufbau sowie die Prinzipien, welche zum Lösen entsprechender Aufgaben anzuwenden sind.
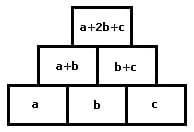
3-reihige Zahlenmauer
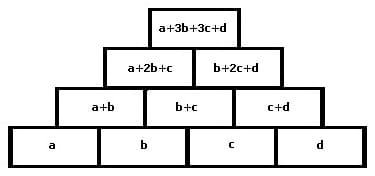
4-reihige Zahlenmauer
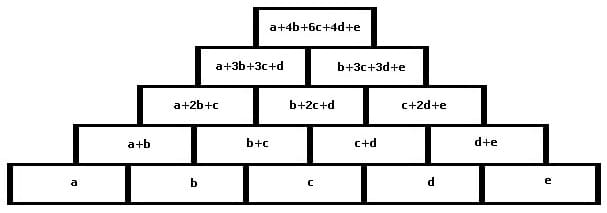
5-reihige Zahlenmauer
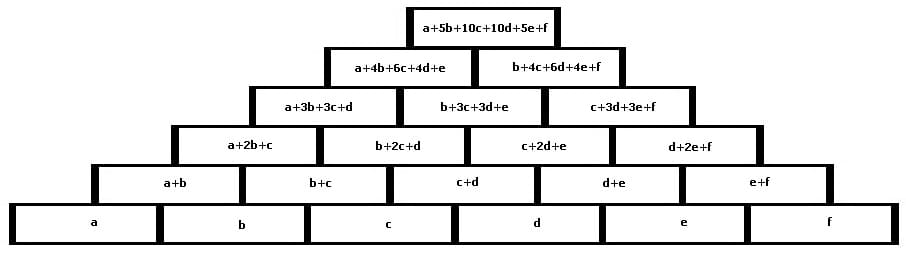
6-reihige Zahlenmauer
Beispiele:
Im Weiteren sind am Beispiel einiger 3-reihiger Zahlenmauern (Rechenmauern) mögliche Aufgabenstellungen sowie deren Lösungen gezeigt. Hierbei sind die fehlenden Zahlen zu ergänzen.
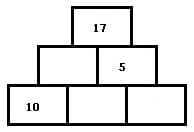
Aufgabenstellung - 1
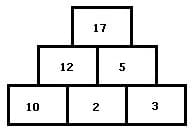
Lösung - 1
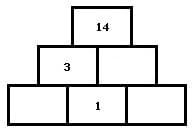
Aufgabenstellung - 2
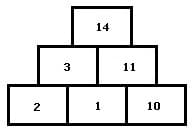
Lösung - 2
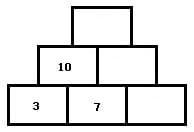
Aufgabenstellung - 3
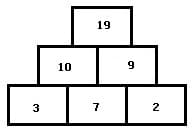
Lösung - 3
Zahlenreihen (Malreihen) sind Anreihungen von Zahlen, die nach einer vorgegebenen Regel bzw. einem Muster aufgelistet werden. Eine Zahlenreihe wird auch als Malreihe bezeichnet. Nachfolgend aufgeführt sind einige häufig benötigte Zahlenreihen.
Zweierreihe:
Unter einer Zweierreihe (Malreihe 2) wird die Menge aller Zahlen verstanden, deren Elemente ohne Rest durch die Zahl 2 teilbar sind. Die Zweierreihe beinhaltet alle ganzzahligen Vielfachen der Zahl 2. Nachfolgend aufgeführt ist die Liste der Zahlen der Zweierreihe bis zur Zahl 600.
0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48 50 52 54 56 58 60 62 64 66 68 70 72 74 76 78 80 82 84 86 88 90 92 94 96 98 100 102 104 106 108 110 112 114 116 118 120 122 124 126 128 130 132 134 136 138 140 142 144 146 148 150 152 154 156 158 160 162 164 166 168 170 172 174 176 178 180 182 184 186 188 190 192 194 196 198 200 202 204 206 208 210 212 214 216 218 220 222 224 226 228 230 232 234 236 238 240 242 244 246 248 250 252 254 256 258 260 262 264 266 268 270 272 274 276 278 280 282 284 286 288 290 292 294 296 298 300 302 304 306 308 310 312 314 316 318 320 322 324 326 328 330 332 334 336 338 340 342 344 346 348 350 352 354 356 358 360 362 364 366 368 370 372 374 376 378 380 382 384 386 388 390 392 394 396 398 400 402 404 406 408 410 412 414 416 418 420 422 424 426 428 430 432 434 436 438 440 442 444 446 448 450 452 454 456 458 460 462 464 466 468 470 472 474 476 478 480 482 484 486 488 490 492 494 496 498 500 502 504 506 508 510 512 514 516 518 520 522 524 526 528 530 532 534 536 538 540 542 544 546 548 550 552 554 556 558 560 562 564 566 568 570 572 574 576 578 580 582 584 586 588 590 592 594 596 598 600
Dreierreihe:
Unter einer Dreierreihe (Malreihe 3) wird die Menge aller Zahlen verstanden, deren Elemente ohne Rest durch die Zahl 3 teilbar sind. Die Dreierreihe beinhaltet alle ganzzahligen Vielfachen der Zahl 3. Nachfolgend aufgeführt ist die Liste der Zahlen der Dreierreihe bis zur Zahl 999.
0 3 6 9 12 15 18 21 24 27 30 33 36 39 42 45 48 51 54 57 60 63 66 69 72 75 78 81 84 87 90 93 96 99 102 105 108 111 114 117 120 123 126 129 132 135 138 141 144 147 150 153 156 159 162 165 168 171 174 177 180 183 186 189 192 195 198 201 204 207 210 213 216 219 222 225 228 231 234 237 240 243 246 249 252 255 258 261 264 267 270 273 276 279 282 285 288 291 294 297 300 303 306 309 312 315 318 321 324 327 330 333 336 339 342 345 348 351 354 357 360 363 366 369 372 375 378 381 384 387 390 393 396 399 402 405 408 411 414 417 420 423 426 429 432 435 438 441 444 447 450 453 456 459 462 465 468 471 474 477 480 483 486 489 492 495 498 501 504 507 510 513 516 519 522 525 528 531 534 537 540 543 546 549 552 555 558 561 564 567 570 573 576 579 582 585 588 591 594 597 600 603 606 609 612 615 618 621 624 627 630 633 636 639 642 645 648 651 654 657 660 663 666 669 672 675 678 681 684 687 690 693 696 699 702 705 708 711 714 717 720 723 726 729 732 735 738 741 744 747 750 753 756 759 762 765 768 771 774 777 780 783 786 789 792 795 798 801 804 807 810 813 816 819 822 825 828 831 834 837 840 843 846 849 852 855 858 861 864 867 870 873 876 879 882 885 888 891 894 897 900 903 906 909 912 915 918 921 924 927 930 933 936 939 942 945 948 951 954 957 960 963 966 969 972 975 978 981 984 987 990 993 996 999
Viererreihe:
Unter einer Vierreihe (Malreihe 4) wird die Menge aller Zahlen verstanden, deren Elemente ohne Rest durch die Zahl 4 teilbar sind. Die Viererreihe beinhaltet alle ganzzahligen Vielfachen der Zahl 4. Nachfolgend aufgeführt ist die Liste der Zahlen der Viererreihe bis zur Zahl 1000.
0 4 8 12 16 20 24 28 32 36 40 44 48 52 56 60 64 68 72 76 80 84 88 92 96 100 104 108 112 116 120 124 128 132 136 140 144 148 152 156 160 164 168 172 176 180 184 188 192 196 200 204 208 212 216 220 224 228 232 236 240 244 248 252 256 260 264 268 272 276 280 284 288 292 296 300 304 308 312 316 320 324 328 332 336 340 344 348 352 356 360 364 368 372 376 380 384 388 392 396 400 404 408 412 416 420 424 428 432 436 440 444 448 452 456 460 464 468 472 476 480 484 488 492 496 500 504 508 512 516 520 524 528 532 536 540 544 548 552 556 560 564 568 572 576 580 584 588 592 596 600 604 608 612 616 620 624 628 632 636 640 644 648 652 656 660 664 668 672 676 680 684 688 692 696 700 704 708 712 716 720 724 728 732 736 740 744 748 752 756 760 764 768 772 776 780 784 788 792 796 800 804 808 812 816 820 824 828 832 836 840 844 848 852 856 860 864 868 872 876 880 884 888 892 896 900 904 908 912 916 920 924 928 932 936 940 944 948 952 956 960 964 968 972 976 980 984 988 992 996 1000
Fünferreihe:
Unter einer Fünferreihe (Malreihe 5) wird die Menge aller Zahlen verstanden, deren Elemente ohne Rest durch die Zahl 5 teilbar sind. Die Fünferreihe beinhaltet alle ganzzahligen Vielfachen der Zahl 5. Nachfolgend aufgeführt ist die Liste der Zahlen der Fünferreihe bis zur Zahl 1000.
0 5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85 90 95 100 105 110 115 120 125 130 135 140 145 150 155 160 165 170 175 180 185 190 195 200 205 210 215 220 225 230 235 240 245 250 255 260 265 270 275 280 285 290 295 300 305 310 315 320 325 330 335 340 345 350 355 360 365 370 375 380 385 390 395 400 405 410 415 420 425 430 435 440 445 450 455 460 465 470 475 480 485 490 495 500 505 510 515 520 525 530 535 540 545 550 555 560 565 570 575 580 585 590 595 600 605 610 615 620 625 630 635 640 645 650 655 660 665 670 675 680 685 690 695 700 705 710 715 720 725 730 735 740 745 750 755 760 765 770 775 780 785 790 795 800 805 810 815 820 825 830 835 840 845 850 855 860 865 870 875 880 885 890 895 900 905 910 915 920 925 930 935 940 945 950 955 960 965 970 975 980 985 990 995 1000
Sechserreihe:
Unter einer Sechserreihe (Malreihe 6) wird die Menge aller Zahlen verstanden, deren Elemente ohne Rest durch die Zahl 6 teilbar sind. Die Sechserreihe beinhaltet alle ganzzahligen Vielfachen der Zahl 6. Nachfolgend aufgeführt ist die Liste der Zahlen der Sechserreihe bis zur Zahl 996.
0 6 12 18 24 30 36 42 48 54 60 66 72 78 84 90 96 102 108 114 120 126 132 138 144 150 156 162 168 174 180 186 192 198 204 210 216 222 228 234 240 246 252 258 264 270 276 282 288 294 300 306 312 318 324 330 336 342 348 354 360 366 372 378 384 390 396 402 408 414 420 426 432 438 444 450 456 462 468 474 480 486 492 498 504 510 516 522 528 534 540 546 552 558 564 570 576 582 588 594 600 606 612 618 624 630 636 642 648 654 660 666 672 678 684 690 696 702 708 714 720 726 732 738 744 750 756 762 768 774 780 786 792 798 804 810 816 822 828 834 840 846 852 858 864 870 876 882 888 894 900 906 912 918 924 930 936 942 948 954 960 966 972 978 984 990 996
Siebenerreihe:
Unter einer Siebenerreihe (Malreihe 7) wird die Menge aller Zahlen verstanden, deren Elemente ohne Rest durch die Zahl 7 teilbar sind. Die Zweierreihe beinhaltet alle ganzzahligen Vielfachen der Zahl 7. Nachfolgend aufgeführt ist die Liste der Zahlen der Siebenerreihe bis zur Zahl 1001.
0 7 14 21 28 35 42 49 56 63 70 77 84 91 98 105 112 119 126 133 140 147 154 161 168 175 182 189 196 203 210 217 224 231 238 245 252 259 266 273 280 287 294 301 308 315 322 329 336 343 350 357 364 371 378 385 392 399 406 413 420 427 434 441 448 455 462 469 476 483 490 497 504 511 518 525 532 539 546 553 560 567 574 581 588 595 602 609 616 623 630 637 644 651 658 665 672 679 686 693 700 707 714 721 728 735 742 749 756 763 770 777 784 791 798 805 812 819 826 833 840 847 854 861 868 875 882 889 896 903 910 917 924 931 938 945 952 959 966 973 980 987 994 1001
Achterreihe:
Unter einer Achterreihe (Malreihe 8) wird die Menge aller Zahlen verstanden, deren Elemente ohne Rest durch die Zahl 8 teilbar sind. Die Achterreihe beinhaltet alle ganzzahligen Vielfachen der Zahl 8. Nachfolgend aufgeführt ist die Liste der Zahlen der Achterreihe bis zur Zahl 1000.
0 8 16 24 32 40 48 56 64 72 80 88 96 104 112 120 128 136 144 152 160 168 176 184 192 200 208 216 224 232 240 248 256 264 272 280 288 296 304 312 320 328 336 344 352 360 368 376 384 392 400 408 416 424 432 440 448 456 464 472 480 488 496 504 512 520 528 536 544 552 560 568 576 584 592 600 608 616 624 632 640 648 656 664 672 680 688 696 704 712 720 728 736 744 752 760 768 776 784 792 800 808 816 824 832 840 848 856 864 872 880 888 896 904 912 920 928 936 944 952 960 968 976 984 992 1000
Neunerreihe:
Unter einer Neunerreihe (Malreihe 9) wird die Menge aller Zahlen verstanden, deren Elemente ohne Rest durch die Zahl 9 teilbar sind. Die Neunerreihe beinhaltet alle ganzzahligen Vielfachen der Zahl 9. Nachfolgend aufgeführt ist die Liste der Zahlen der Neunerreihe bis zur Zahl 1440.
0 9 18 27 36 45 54 63 72 81 90 99 108 117 126 135 144 153 162 171 180 189 198 207 216 225 234 243 252 261 270 279 288 297 306 315 324 333 342 351 360 369 378 387 396 405 414 423 432 441 450 459 468 477 486 495 504 513 522 531 540 549 558 567 576 585 594 603 612 621 630 639 648 657 666 675 684 693 702 711 720 729 738 747 756 765 774 783 792 801 810 819 828 837 846 855 864 873 882 891 900 909 918 927 936 945 954 963 972 981 990 999 1008 1017 1026 1035 1044 1053 1062 1071 1080 1089 1098 1107 1116 1125 1134 1143 1152 1161 1170 1179 1188 1197 1206 1215 1224 1233 1242 1251 1260 1269 1278 1287 1296 1305 1314 1323 1332 1341 1350 1359 1368 1377 1386 1395 1404 1413 1422 1431 1440
Zehnerreihe:
Unter einer Zehnerreihe (Malreihe 10) wird die Menge aller Zahlen verstanden, deren Elemente ohne Rest durch die Zahl 10 teilbar sind. Die Zehnerreihe beinhaltet alle ganzzahligen Vielfachen der Zahl 10. Nachfolgend aufgeführt ist die Liste der Zahlen der Zehnerreihe bis zur Zahl 2000.
0 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250 260 270 280 290 300 310 320 330 340 350 360 370 380 390 400 410 420 430 440 450 460 470 480 490 500 510 520 530 540 550 560 570 580 590 600 610 620 630 640 650 660 670 680 690 700 710 720 730 740 750 760 770 780 790 800 810 820 830 840 850 860 870 880 890 900 910 920 930 940 950 960 970 980 990 1000 1010 1020 1030 1040 1050 1060 1070 1080 1090 1100 1110 1120 1130 1140 1150 1160 1170 1180 1190 1200 1210 1220 1230 1240 1250 1260 1270 1280 1290 1300 1310 1320 1330 1340 1350 1360 1370 1380 1390 1400 1410 1420 1430 1440 1450 1460 1470 1480 1490 1500 1510 1520 1530 1540 1550 1560 1570 1580 1590 1600 1610 1620 1630 1640 1650 1660 1670 1680 1690 1700 1710 1720 1730 1740 1750 1760 1770 1780 1790 1800 1810 1820 1830 1840 1850 1860 1870 1880 1890 1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 2000
Unter der Vielfachenmenge wird die Menge aller Vielfacher einer natürlichen Zahl verstanden. Sie setzt sich aus natürlichen Zahlen zusammen, welche ohne Rest durch die entsprechende Ausgangszahl teilbar sind.
Beispiele:
4·1 = 4
4·2 = 8
4·3 = 12
4·4 = 16
5·4 = 20
.
.
.
usw.
5·1 = 5
5·2 = 10
5·3 = 15
5·4 = 20
5·5 = 25
.
.
.
usw.
Alle ganzen Zahlen (>= 0), die addiert eine bestimmte Zahl ergeben, werden als Partnerzahlen (verliebte Zahlen) bezeichnet. Verliebte Zahlen ergeben addiert stets die entsprechende Zahl. Nachfolgend gezeigte Listen gewähren einen Einblick in einige verliebte Zahlen (Partnerzahlen).
die Zahl 0 liebt die Zahl 1, denn 0 + 1 = 1
die Zahl 1 liebt die Zahl 0, denn 1 + 0 = 1
die Zahl 0 liebt die Zahl 3, denn 0 + 3 = 3
die Zahl 1 liebt die Zahl 2, denn 1 + 2 = 3
die Zahl 2 liebt die Zahl 1, denn 2 + 1 = 3
die Zahl 3 liebt die Zahl 0, denn 3 + 0 = 3
die Zahl 0 liebt die Zahl 5, denn 0 + 5 = 5
die Zahl 1 liebt die Zahl 4, denn 1 + 4 = 5
die Zahl 2 liebt die Zahl 3, denn 2 + 3 = 5
die Zahl 3 liebt die Zahl 2, denn 3 + 2 = 5
die Zahl 4 liebt die Zahl 1, denn 4 + 1 = 5
die Zahl 5 liebt die Zahl 0, denn 5 + 0 = 5
die Zahl 0 liebt die Zahl 10, denn 0 + 10 = 10
die Zahl 1 liebt die Zahl 9, denn 1 + 9 = 10
die Zahl 2 liebt die Zahl 8, denn 2 + 8 = 10
die Zahl 3 liebt die Zahl 7, denn 3 + 7 = 10
die Zahl 4 liebt die Zahl 6, denn 4 + 6 = 10
die Zahl 5 liebt die Zahl 5, denn 5 + 5 = 10
die Zahl 6 liebt die Zahl 4, denn 6 + 4 = 10
die Zahl 7 liebt die Zahl 3, denn 7 + 3 = 10
die Zahl 8 liebt die Zahl 2, denn 8 + 2 = 10
die Zahl 9 liebt die Zahl 1, denn 9 + 1 = 10
die Zahl 10 liebt die Zahl 0, denn 10 + 0 = 10
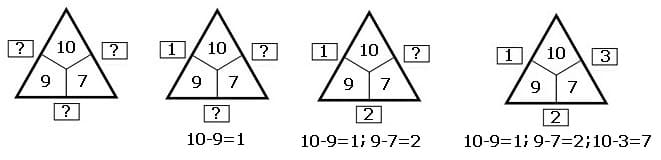
Zahlendreiecke (Rechendreiecke) werden eingesetzt um Schülern der Grundschule das Üben des Addierens und des Subtrahierens zu ermöglichen. Es können mehrere Varianten derartiger Aufgaben ausgeführt werden. Zwei dieser sind nachfolgend aufgeführt. Auch wird der zu durchlaufende Rechenweg aufgezeigt.
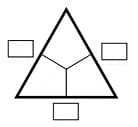
Variante 1:
Das Ergebnis zweier Zahlen die sich im Inneren des Rechendreiecks befinden ist außen an die sich zwischen zwei Feldern befindende Stelle zu schreiben. Bei der Durchführung einer Addition (Plus-Aufgabe) ist die Summe dieser beiden Zahlen in das dafür vorgesehene Feld einzutragen. Beim Ausführen einer Subtraktion (Minus-Aufgabe) ist dies mit der Differenz derer durchzuführen.
Variante 2:
Zu einer sich außerhalb des Dreiecks befindenden Zahl ist im Inneren des Dreiecks das Ergebnis einer Addition oder Subtraktion in das zur äußeren Zahl benachbarte Feld einzutragen.
Die im Folgenden gezeigten Bilder demonstrieren Beispiele zur prinzipiellen Ausführung des Verfahrens mit der Addition. Die mit Fragezeichen versehenen Kästchen sind mit den entsprechenden Zahlen zu versehen.
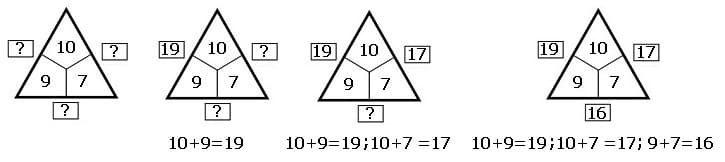
Die nachfolgend dargestellten Bilder demonstrieren Beispiele zur prinzipiellen Ausführung des Verfahrens mit der Subtraktion. Die mit Fragezeichen versehenen Kästchen sind mit den entsprechenden Zahlen zu versehen.
Gliederungsbaum: Ein Term kann mit Hilfe eines Gliederungsbaums oder eines Rechenbaums übersichtlich dargestellt werden.
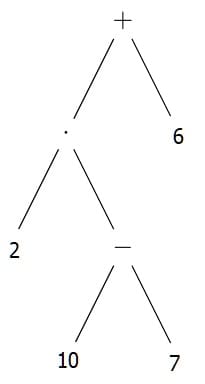
Abb. 1 Beispiel - Gliederungsbaum für den Term 2⋅(10−7)+6
Hierbei wird mit dem Rechenschritt begonnen, die zuerst ausgeführt werden würde. Diese bildet das ganz unten angeordnete Astpaar. Ab dem zweiten erforderlichen Rechenschritt wird das darüber angeordnete Astpaar gezeichnet und beschriftet. Diese Vorgehensweise wird bis zur vollständigen Abbildung des gesamten Terms von unten nach oben durchgeführt.
Rechenbaum: Rechenbäume ermöglichen das Erlernen der Grundrechenarten. Dies sind die Addition, die Subtraktion, die Multiplikation sowie die Division. Anwendung findet er in der Grundschule.
Hierbei gilt es, leere Kästchen des entsprechenden Rechenbaums unter Berücksichtigung der vorgegebenen Rechenart mit korrekten Zahlenwerten zu füllen. Durchlaufen werden die einzelnen Schritte von oben nach unten und / bzw. von links nach rechts.
Nach einer Durchführung der vorgegebenen Grundrechenart mit den gegeben Zahlen werden die Ergebnisse (im Folgenden rot markiert) in die dafür vorgesehenen leeren Felder (Kästchen) eingetragen.
Die anschließend wiedergegebenen Abbildungen zeigen Bäume dieser Art in verschiedenen Ausführungen, mit sowie ohne Berechnungsergebnisse (Ergänzungen):
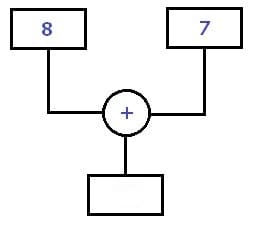
Rechenbaum - Struktur - Bild 1
Rechenbaum - Struktur - Bild 2
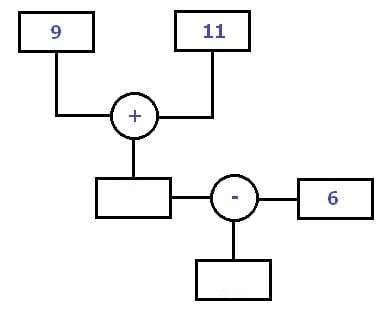
Rechenbaum - Struktur - Bild 3
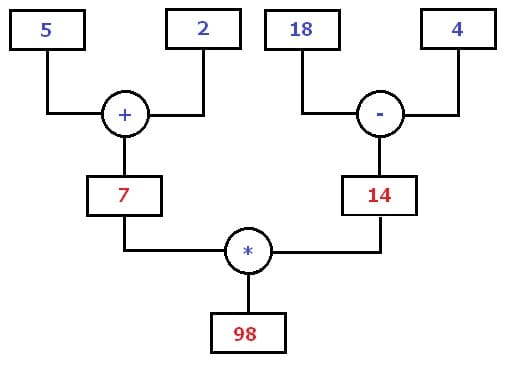
Rechenbaum - Struktur - Bild 4
Beispiele:
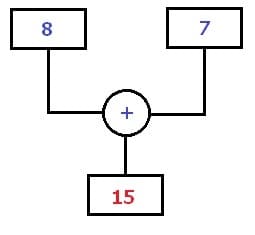
Rechenbaum - Beispiel 1 (Addieren):
Im nachfolgend dargestellten Rechenbaum sind die beiden Zahlen 3 und 8 zu addieren. Dieser auszuführende Rechenschritt führt zum Ergebnis 3 + 8 = 11.
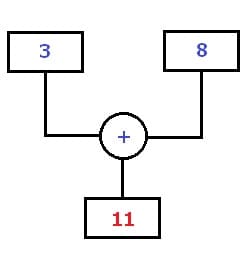
Rechenbaum - Beispiel - Addition
Rechenbaum - Beispiel 2 (Subtrahieren):
Die folgende Aufgabe besteht darin, die Zahl 5 von der Zahl 12 zu subtrahieren (abzuziehen). Nach Durchführung der Rechenoperation 12 - 5 resultiert das Ergebnis 12 - 5 = 7.
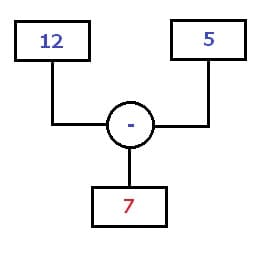
Rechenbaum - Beispiel - Subtraktion
Rechenbaum - Beispiel 3 (Multiplizieren):
Es gilt den unten gezeigten Rechenbaum zu vervollständigen. Hierbei ist eine Multiplikation der beiden Zahlen 4 und 5 durchzuführen. Dies führt zum Ergebnis 4 * 5 = 20.
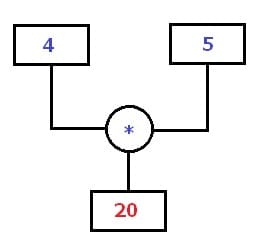
Rechenbaum - Beispiel - Multiplikation
Rechenbaum - Beispiel 4 (Dividieren):
Das nächste Beispiel zeigt die Ausführung einer Division der Zahl 27 durch die Zahl 9. Hierbei ist die Zahl 3 in das entsprechende Feld einzutragen, denn die Division der Zahlen 27 : 9 ergibt das Resultat 27 : 9 = 3.
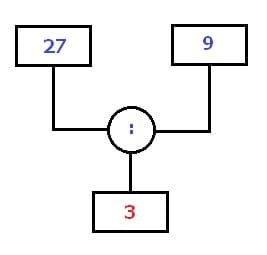
Rechenbaum - Beispiel - Division
Zahlenhäuser (Rechenhäuser) werden dazu verwendet, um die Grundrechenarten zu üben. Im Dach des entsprechenden Hauses befindet sich der Operator sowie die Zahl, mit welcher die festgelegte Rechenart durchgeführt werden soll.
Zahlenhaus - Rechenhaus - Muster
In den nachfolgend gezeigten Beispielen ist stets die Addition durchzuführen. Im jeweiligen leeren Feld (rechtsseitig oder linksseitig angeordnet) ist die gesuchte Zahl (das Ergebnis der durchzuführenden Rechenoperation) einzutragen.
Zahlenhaus - Rechenhaus - Beispiel 1
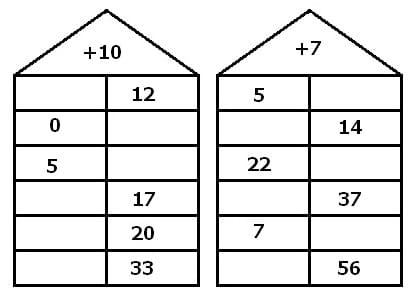
Zahlenhaus - Rechenhaus - Beispiel 2
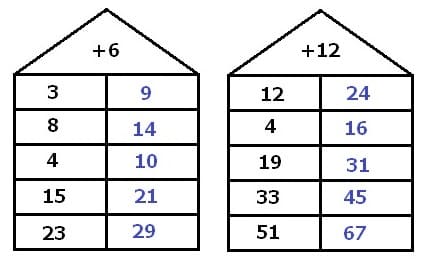
Zahlenhaus - Rechenhaus - Beispiel 3
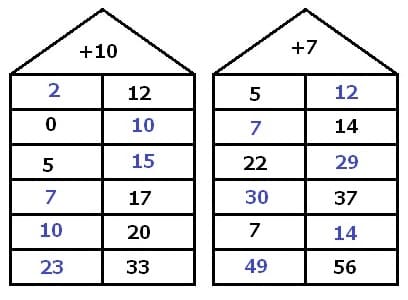
Zahlenhaus - Rechenhaus - Beispiel 4
Das Hunderterfeld (die Hundertertafel) dient im Schulunterricht zum Kennenlernen des Zahlenraums bis 100. Es besteht aus 10 Zeilen und 10 Spalten in Form eines Quadrats. Mit jeder Reihe und jeder Spalte beginnt ein neues Zehnerfeld. Hierbei gilt es, fehlende Zahlen zu ergänzen und somit entsprechende Nachbarzahlen einzutragen und kennzulernen. Die dargestellten Zahlen wachsen stets in Einerschritten an und beginnen oben links mit der Zahl 1.
Nachfolgend dargestellt sind einige Bilder zu Hundertertafeln.

Hundertertafel - Hunderterfeld - Vorlage (leer)
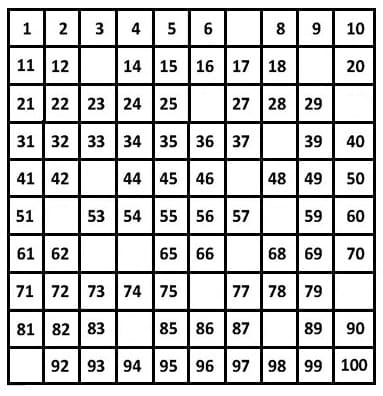
Hundertertafel - Hunderterfeld - Muster
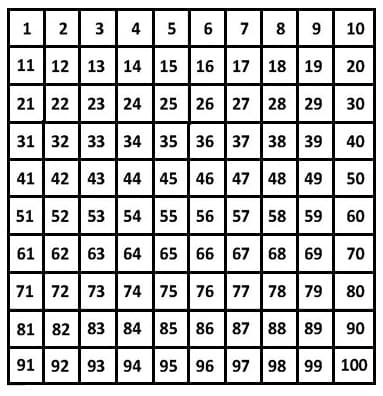
Hundertertafel - Hunderterfeld - Vollständig ausgefüllt
Als Dreieckszahlen werden natürliche Zahlen bezeichnet, die grafisch in Form von Dreiecken darstellbar sind. Ihre Bezeichnung beruht auf ihrer grafischen Darstellbarkeit.
Es wird die Zahl 1 vorgegeben und hierauf die nachfolgende ganze Zahl addiert. Diese wird, wie nachfolgend gezeigt in die nächste darunterliegende Zeile geschrieben.
1
1+2 = 3
(1+2)+3 = 6
(1+2+3)+4 = 10
(1+2+3+4)+5 = 15
(1+2+3+4+5)+6 = 21
Nachfolgend dargestellt sind die ersten 5 Dreieckszahlen:
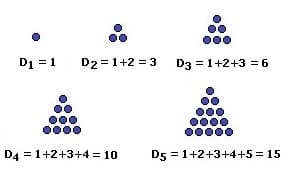
Allgemein lassen sich Dreieckzahlen in der Form dn = 1 + 2 + 3 + 4 + 5 ...+ (n-2) + (n-1) + n darstellen.
Mittels der Formel dn = n · (n + 1) / 2 können Zahlen dieser Art als Folge beschrieben werden.
Die ersten Dreieckszahlen zwischen 1 und 1000 sind:
1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741, 780, 820, 861, 903, 946 und 990.
Die Spiegelzahl oder Umkehrzahl einer mehrstelligen natürlichen Zahl wird gebildet, indem deren Ziffern in umgekehrter Reihenfolge geschrieben werden.
Beispiele zu Spiegelzahlen (Umkehrzahlen):
Die Spiegelzahl (Umkehrzahl) zu 12345 ist die Zahl 54321.
Die Spiegelzahl (Umkehrzahl) zu 6872 ist die Zahl 7286.
Als magisches Quadrat (Zahlenquadrat oder Zauberquadrat) wird ein schachbrettförmiges Quadrat bezeichnet, dessen Felder mit Zahlen (Zeichen oder Symbolen) versehen sind und auf bestimmte Art und Weise miteinander in Verbindung stehen. Hierbei werden auf einem Quadrat der Ordnung n (mit der Seitenlänge n) n2 unterschiedliche natürliche Zahlen derart angeordnet, dass jede Zeile und jede Spalte bei Durchführung einer Addition dieser eingetragenen Zahlen wie auch die beiden Diagonalen die gleiche Summe ergeben.
Zauberquadrate (magische Quadrate, Zahlenquadrate) besitzen die Eigenschaft, dass die Summen einzelner Zeilen, Spalten und Diagonalen stets gleich groß sind.
Beispiele:
Nachfolgend aufgeführt sind zwei ausgefüllte Beispiele zu magischen Quadraten.
Beispiel 1 - Magisches Quadrat 3x3:
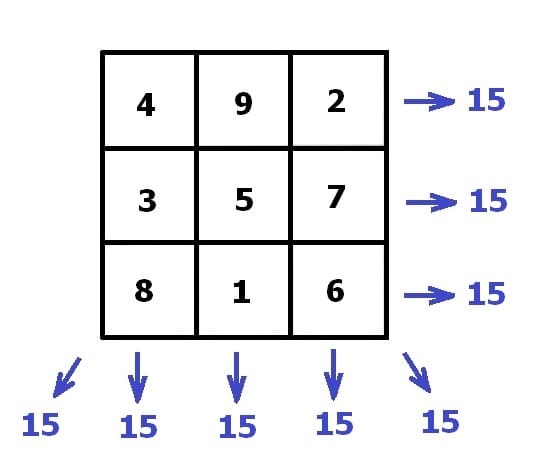
Im vorliegenden Fall ergeben sich bei der Bildung dieser einzelnen Summen folgende Zusammenhänge und Ergebnisse:
Erste Zeile: 4 + 9 + 2 = 15
Zweite Zeile: 3 + 5 + 7 = 15
Dritte Zeile: 8 + 1 + 6 = 15
Erste Spalte: 4 + 3 + 8 = 15
Zweite Spalte: 9 + 5 + 7 = 15
Dritte Spalte: 8 + 1 + 6 = 15
Diagonale 1: 2 + 5 + 8 = 15
Diagonale 2: 4 + 5 + 6 = 15
Hierbei kann festgestellt werden, dass sich bei all diesen derartig durchgeführten Summenbildungen stets ein Wert von 15 ergibt.
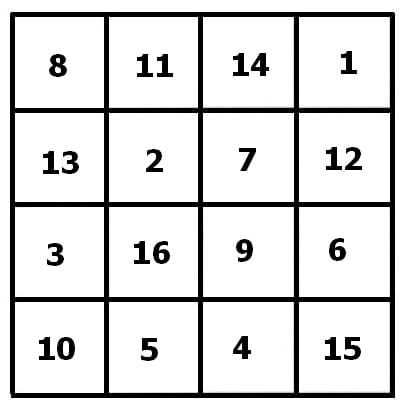
Beispiel 2 - Magisches Quadrat 4x4:
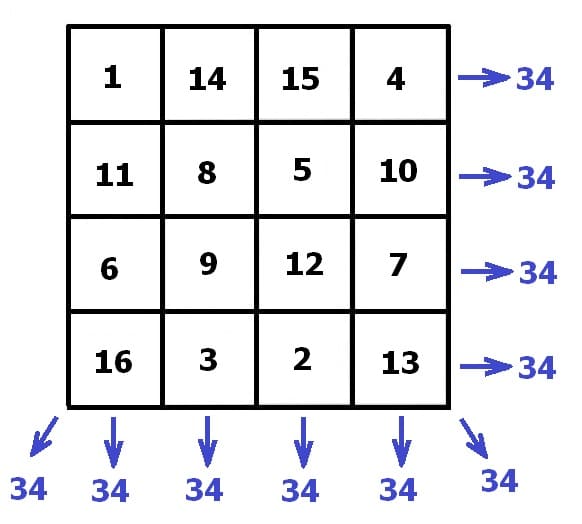
Im vorliegenden Fall ergeben sich bei der Bildung dieser einzelnen Summen folgende Zusammenhänge und Ergebnisse:
Erste Zeile: 1 + 14 + 15 + 4 = 34
Zweite Zeile: 11 + 8 + 5 + 10 = 34
Dritte Zeile: 6 + 9 + 12 + 7 = 34
Vierte Zeile: 16 + 3 + 2 + 13 = 34
Erste Spalte: 1 + 11 + 6 + 16 = 34
Zweite Spalte: 14 + 8 + 9 + 3 = 34
Dritte Spalte: 15 + 5 + 12 + 2 = 34
Vierte Spalte: 4 + 10 + 7 + 13 = 34
Diagonale 1: 4 + 5 + 9 + 16 = 34
Diagonale 2: 1 + 9 + 12 + 13 = 34
Hierbei kann festgestellt werden, dass sich bei all diesen derartig durchgeführten Summenbildungen stets ein Wert von 34 ergibt.
Beispiel der schrittweisen Ergänzung fehlender Zahlen.
Von nachfolgend gezeigtem magischem Quadrat sei bekannt, dass seine Summe 15 sein muss. Durch aufeinanderfolgendes schrittweises Ergänzen (Ausfüllen der entsprechenden Felder mit der fehlenden Zahl) erfolgt die Vervollständigung dessen.
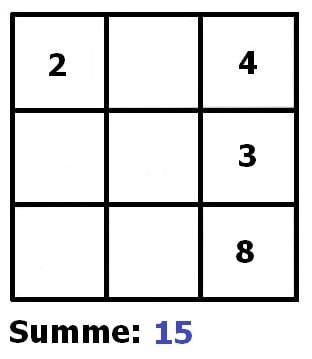
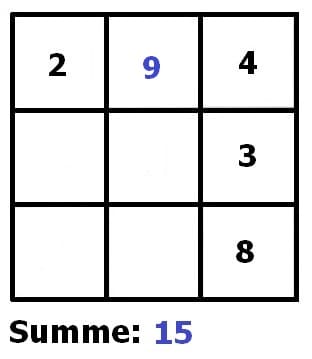
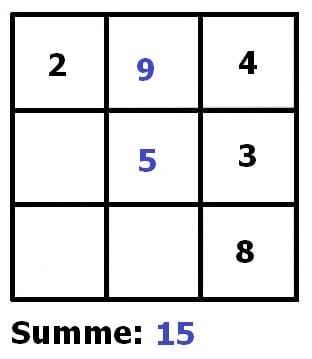
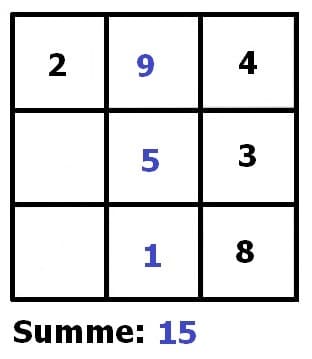
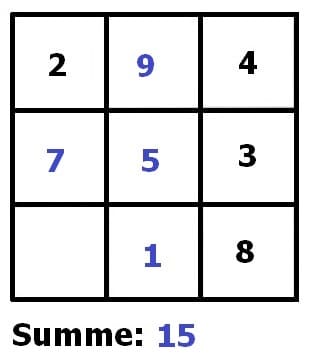
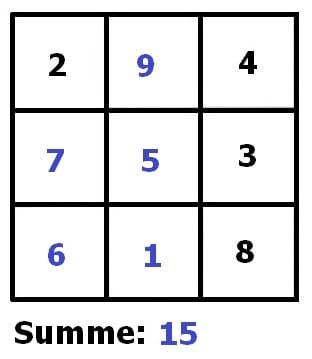
Weitere Beispiele:
Im Folgenden sind die Grafiken einiger weiterer magischer Quadrate abgebildet.
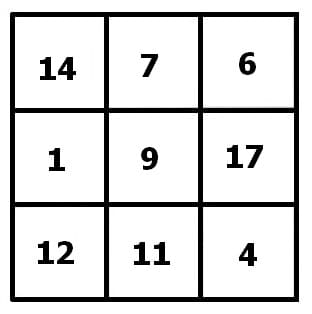
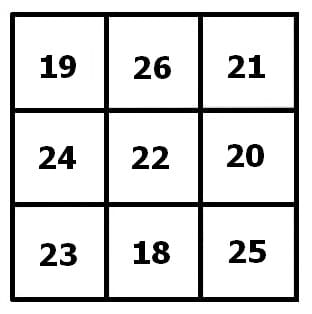
Bei einer Rechentabelle bzw. Rechentafel handelt es sich um eine Tabelle, die nachfolgend gezeigte Gestalt besitzt.
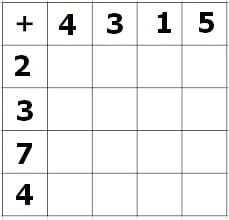
Mit Hilfe von Rechentabellen (Rechentafeln) können die Grundrechenarten geübt werden. Sie bestehen aus m Zeilen und n Spalten und verfügen über die Möglichkeit m x n einzelne Aufgaben berechnen zu lassen. Im links oben positionierten Feld befindet sich das Operationszeichen das die Art der mit der Rechentabelle durchzuführenden Rechenoperationen enthält. Dies kann in der Regel die Addition (Plus +), die Subtraktion (Minus -), die Multiplikation (Mal *) oder die Division (Divisionssymbol /) sein. Beim jeweiligen Schnittpunkt (Kreuzungspunkt) einer Zeile sowie einer Spalte wird das entsprechende Rechenergebnis eingetragen.
Beispiel:
In der nachfolgend dargestellten Abbildung ist eine Rechentafel gezeigt, mit welcher Additionen durchgeführt wurden.
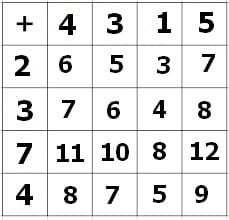
Zum Ausfüllen der zuvor gezeigten Rechentabelle wurden folgende Rechenoperationen ausgeführt.
4 + 2 = 6
4 + 3 = 7
4 + 7 = 11
4 + 4 = 8
3 + 2 = 5
3 + 3 = 6
3 + 7 = 10
3 + 4 = 7
1 + 2 = 3
1 + 3 = 4
1 + 7 = 8
1 + 4 = 5
5 + 2 = 7
5 + 3 = 8
5 + 7 = 12
5 + 4 = 9
Umkehraufgaben:
Als das Bearbeiten einer Umkehraufgabe wird der Vorgang bezeichnet, eine gegenteilige Rechenoperation mit gegebenen Zahlen auszuführen. Wird beispielsweise eine Addition zweier Zahlen durchgeführt, so wird bei der Bearbeitung einer entsprechenden Umkehraufgabe mit diesen Zahlen eine Subtraktion durchgeführt. Die Umkehraufgabe zu einer Divisionsaufgabe ist eine Multiplikationsaufgabe.
Tauschaufgaben:
Als Tauschaufgaben werden Aufgaben bezeichnet, mit denen Grundrechenarten, die auf dem Kommutativgesetz (Vertauschungsgesetz) basieren, bearbeitet werden. Sie können ausschließlich mit den beiden Grundrecharten Addition und Multiplikation durchgeführt werden, da es hierbei nicht von Relevanz ist, in welcher Reihenfolge die entsprechende Rechenoperation mit zwei Zahlen ausgeführt wird. Für die Rechenarten Subtraktion und Division bestehen hingegen keine Möglichkeiten Tauschaufgaben zu berechnen.
Bei Durchführung der nachfolgend gezeigten Rechenoperationen (Additionen) ist es nicht relevant, in welcher Reihenfolge die entsprechende Operation ausgeführt wird. Es resultiert in beiden Fällen das gleiche Ergebnis.
Nachfolgend aufgeführt sind einige Beispiele zu Tauschaufgaben.
Beispiel 1 - Addition:
3 + 5 = 8
5 + 5 = 8
Beispiel 2 - Addition:
4 + 1 = 5
1 + 4 = 5
Beispiel 3 - Multiplikation:
3 · 2 = 6
2 · 3 = 6
Beispiel 4 - Multiplikation:
6 · 7 = 42
7 · 6 = 42
Platzhalteraufgaben - Ergänzungsaufgaben - Lückenaufgaben:
Als Ergänzungsaufgaben (Platzhalteraufgaben oder Lückenaufgaben) werden Aufgaben der Mathematik bezeichnet, bei welchen nicht alle Informationen vorhanden sind, um eine wahre oder falsche Aussage zum vorliegenden Sachverhalt machen zu können. Vielmehr wird dabei verlangt, den entsprechenden Platzhalter mit einer relevanten Zahl zu versehen.
Beispiel 1:
5 + __ = 8
Die Lösung dieser Aufgabe lautet 3, denn 5 + 3 = 8
Beispiel 2:
8 - __ = 4
Die Lösung dieser Aufgabe lautet 4, denn 8 - 4 = 4
I - Kettenaufgabe (Rechenkette):
Als Kettenaufgabe (Rechenaufgabe) wird die Aneinanderreihung mehrerer in einer Aufgabe vorkommender Rechenoperationen bezeichnet, bei der alle Grundrechenarten vorkommen können. Die nachfolgende Beschreibung derartiger Operationen bei Kettenaufgaben bzw. Rechenketten bezieht sich im vorliegenden Fall auf die Addition, die Subtraktion, die Multiplikation und die Division.
Bei der Ausführung der Berechnung der nachfolgend gezeigten Aufgaben sind aufeinanderfolgend mehrere Rechenoperationen der gleichen Art (Additionen) durchzuführen. Etappenweise werden hierbei mehrere Zahlen nacheinander addiert.
Beispiel 1:
Es ist die folgende Kettenaufgabe zu lösen: 4 + 2 + 8.
Lösungsweg:
4 + 2 + 8 =
6 + 8 =
14
oder:
4 + 2 + 8 = 6 + 8 = 14
Beispiel 2:
Es ist die folgende Kettenaufgabe zu lösen: 5 + 3 + 1 + 6.
Lösungsweg:
5 + 3 + 1 + 6 =
8 + 1 + 6 =
9 + 6 =
15
oder:
5 + 3 + 1 + 6 = 15
Bei der Ausführung der Berechnung der nachfolgend gezeigten Aufgaben sind aufeinanderfolgend mehrere Rechenoperationen der gleichen Art (Multiplikationen) durchzuführen. Etappenweise werden hierbei mehrere Zahlen nacheinander miteinander multipliziert.
Beispiel 3:
Es ist die folgende Kettenaufgabe zu lösen: 3 · 5 · 4.
Lösungsweg:
3 · 5 · 4 =
15 · 4 =
60
oder:
3 · 5 · 4 = 15 · 4 = 60
Beispiel 4:
Es ist die folgende Kettenaufgabe zu lösen: 2 · 3 · 4 · 5.
Lösungsweg:
2 · 3 · 4 · 5 =
6 · 4 · 5 =
24 · 5 =
120
oder:
2 · 3 · 4 · 5 = 120
Bei der Ausführung der Berechnung der nachfolgend gezeigten Aufgaben sind aufeinanderfolgend mehrere Rechenoperationen unterschiedlicher Arten (Multiplikationen und Additionen) durchzuführen. Hierbei gilt es, die Punkt-Vor-Strich-Rechnung zu beachten und die Zahlen gemäß dieser Gesetzmäßigkeit zunächst miteinander zu multiplizieren und hierauf zu addieren.
Beispiel 5:
Es ist die folgende Kettenaufgabe zu lösen: 3 + 8 · 2 + 5 · 2.
Lösungsweg:
3 + 8 · 2 + 5 · 2 =
3 + 16 + 5 · 2 =
3 + 16 + 10 =
19 + 10 =
29
oder:
3 + 8 · 2 + 5 · 2 = 3 + 16 + 10 = 29
II - Rechenschlange - Rechenkette:
Rechenschlangen: In ähnlicher Weise wie bei Kettenaufgaben (Rechenketten), erfolgt bei Rechenschlangen das Aneinanderreihen mehrerer Aufgaben, bei denen stets mit dem Resultat der vorhergehenden Aufgabe weitergerechnet wird. Da es der Übung des Kopfrechnens dienen soll, erfolgt in diesem Fall kein Niederschreiben des ermittelten Zwischenergebnisses.
Fermi-Fragen - Fermi-Aufgaben:
Unter einer Fermi-Frage wird die mengenmäßige Abschätzung zur Lösung einer Aufgabe verstanden, für die zunächst nahezu keine Daten vorhanden sind. Eine Aufgabe dieser Art ist nach dem italienischen Physik-Nobelpreisträger Enrico Fermi (1901-1954) benannt und wird als Fermi-Aufgabe bezeichnet. Da sie zur derer Beantwortung lediglich wenige Informationen beinhalten, ist die Durchführung entsprechender Recherechen notwendig, um entsprechende Abschätzungen vernünftig begründen zu können.
Aufgaben dieser Art lassen in der Regel weder eine exakte Antwort, noch einen ausschließlich einzigen Lösungsweg zu. Sie eignen sich zur Freiarbeit sowie für den offenen Unterricht.
Beispiele für Fermi-Fragen:
Wie viel Flüssigkeit nimmt ein Mensch in einem Jahr zu sich?
Wie oft erfolgt ein Blinzeln binnen einesTages?
Wie viele Sandkörner beinhaltet ein Sandkasten?
Wie viele Blätter befinden sich an einem Baum?
Als Kapitänsaufgaben werden Aufgaben bezeichnet, die aufgrund des Fehlens von Angaben nicht lösbar sind, oder deren Fragestellungen nicht zur Aufgabe passen.
Ein Beispiel für eine derartige Aufgabe ist nachfolgend aufgeführt:
Auf einem befinden sich 24 Zeigen und 8 Schafe. Wie alt ist der Kapitän dieses Schiffs?
Zu Beginn der 80er Jahre legte die Arbeitsgruppe des französischen Forschungsinstituts für den Mathematikunterricht einer Gruppe von 97 Kindern der zweiten und dritten Klasse diese Aufgabe vor. Es resultierte folgendes Ergebnis:
76 der 97 befragten Schüler (und somit 80%) lösten diese Aufgabe indem sie unterschiedliche Kombinationen mit diesen beiden Zahlen durchführten.
Mit Hilfe von Punktebildern (Punktefeldern) lassen sich Schülern der Grundschule logische Rechenvorgänge unter Verwendung des Einmaleins veranschaulichen. Deren Verwendung fördert die Wahrnehmung, das logische Denken sowie die Konzentration der Kinder. Mittels der bildhaften Gestaltung von Aufgaben dieser Art können bestimmte Rechenstrategien einfacher umgesetzt werden.
Durch dauerhaftes Üben mit Arbeitsblättern für Punktefelder können Schüler ihr Wissen bezüglich des Einmaleins vertiefen.

Punktebilder - Punktefelder - Abb. 1
Punktebilder - Punktefelder - Abb. 2
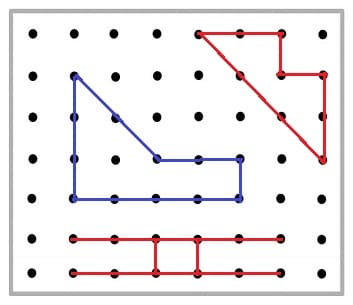
Punktebilder - Punktefelder - Abb. 3
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema in Mathe (Matheaufgaben). Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet der Mathematik, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden.
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Zahlengerade zu finden.
Römische Zahlen - Schriftliche Addition - Schriftliche Subtraktion - Schriftliche Multiplikation - Schriftliche Division - Schriftliche Potenzierung - Aussagenlogik - Zahltypumwandlung - Zinsrechnung - Zinseszinsrechnung grafisch - Annuitätentilgung - Jahreszinsrechnung - Physikalische Größen - Materialkonstanten - Fachbegriffe Deutsch - Englisch - Mandelbrot- und Juliamengen - Zusammenhänge Mandelbrot-Juliamengen - Sierpinski-Dreieck - Koch-Kurve - Pythagoras-Baum - Feigenbaum-Diagramm - Lindenmayer-System - Lindenmayer-System II - Logistische Gleichung I - Logistische Gleichung II - Diagramme - Tortendiagramm - Kryptografie - Raumgittermodelle (3D) - Paare geordnet - Kalender - Rechnen mit selbstdefinierten Formeln - Zeichenprogramm - Tangram - Tetris - Spiel 15 - Türme von Hanoi - Dame - Schach
MathProf 5.0 - Unterprogramm Römische Zahlen

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















