MathProf - Zahlenbereiche - Zahlenmengen - Perrin-Zahlen

Fachthemen: Spezielle Zahlen II - Zahlenmengen - Zahlenbereiche
MathProf - Algebra - Software für numerische und interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Durchführung verschiedener numerischer
Analysen mit ganzen Zahlen.
In diesem Teilprogramm wird unter anderem das Berechnen von Partitionen, Perrin-Zahlen, undulierenden Zahlen, Gray-Code-Zahlen, biquadratischen Tupel sowie von abundanten und defizienten Zahlen ermöglicht. Der Rechner gibt die ermittelten Ergebnisse in einer Liste aus.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben, sind implementiert.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Zahlenbereiche - Zahlenmengen - Zahlbereichserweiterung - Partition - Partitionen - Perrin-Zahlen - Undulierende Zahlen - Multiplikative Beharrlichkeit - k-Permutationen - Quasi befreundete Zahlen - Zeckendorf-Zerlegung - Zerlegungen - Reihenfolge - Summe - Formel - Teiler - Fibonacci-Folge - Natürliche Zahlen - Gray-Code - Biquadratische Tupel - Natürliche Zahl - Zahl - Vollkommene Zahl - Zerlegung - Zahlzerlegung - Summanden - Perrin-Folge - Algebraische Zahlenfolge - Padovan-Folge - Beharrlichkeit - Einführung - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Herleitung - Beweis - Lernen - Erlernen - Begriff - Begriffe - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Übersicht - Paare - Glieder - Neutrales Element - Neutrale Elemente - Ergebnis - Befreundete Zahlen - Zeckendorf-Theorem - Zahlentheorie - Vollkommene Zahlen - Abundante Zahlen - Defiziente Zahl - Berechnen - Untersuchen - Untersuchung - Tabelle - Liste - 0 - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 11 - 12 - 13 - 14 - 15 - 16 - 17 - 18 - 19 - 20 - Berechnung - Werte - Zerlegen - Elemente - Mengendiagramm - Ganze Zahlen - Zahlenart - Zahlenarten - Zahlenmenge - Zahlenmenge N - Zahlenmenge Q - Zahlenmenge R - Zahlenmenge C - Alternierende Quersumme - Quersumme - Quersummen - Quersummenregel - Ziffernsumme - Einstellige Quersumme - Iterierte Quersumme - Gerade Quersumme - Ungerade Quersumme - Zuordnen - Zuordnung - Grundzahlen - Kardinalzahlen - Gebrochene Zahlen - Rationale Zahlen - Reelle Zahlen - Transzendente Zahlen - Erklärung - Einfach erklärt - Beschreibung - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Mathe - Mathematik - Anwendungsaufgaben - Definition - Wie - Weshalb - Was ist - Warum - Was sind - Welche - Welcher - Welches - Wodurch - Bedeutung - Was bedeutet - Übersicht - Zeichen - Grundlagen - Zahlen - Finden - Eineindeutig - Bezeichnung - Bezeichnungen - Bereich - Bereiche - N - G - Q - C - R - Menge - Mengen - Negative Zahlen - Positive Zahlen - Negative Dezimalzahl - Positive Dezimalzahl - Negative Dezimalzahlen - Positive Dezimalzahlen - Negative reelle Zahlen - Positive reelle Zahlen - Negative rationale Zahlen - Positive rationale Zahlen - Multiplizieren rationaler Zahlen - Dividieren rationaler Zahlen - Multiplikation rationaler Zahlen - Division rationaler Zahlen - Menge der natürlichen Zahlen - Menge der ganzen Zahlen - Menge der rationalen Zahlen - Menge der rellen Zahlen - Menge der komplexen Zahlen - Symbole - Rechner - Einerstelle - Zehnerstelle - Hunderterstelle - Tausenderstelle - Einer - Zehner - Hunderter - Tausender - Stellenschreibweise |
Zahlen II
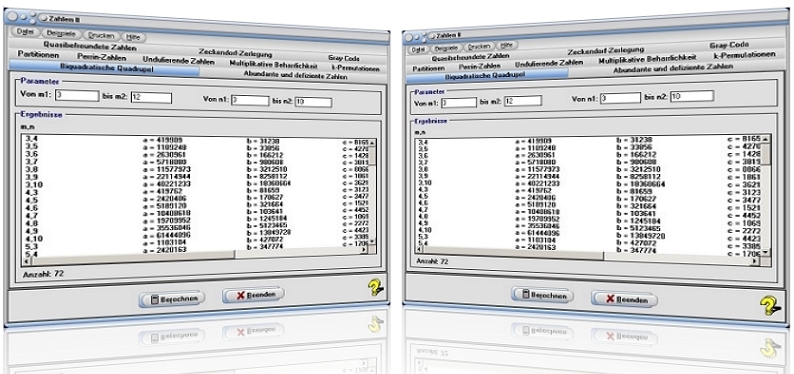
Modul Zahlen II
Das Unterprogramm [Algebra] - [Zahlen] - Zahlen II ermöglicht die Durchführung verschiedener numerischer Berechnungen.

Hierbei stehen Untersuchungen zu folgenden Themengebieten zur Auswahl:
- Partitionen
- Perrin-Zahlen
- Undulierende Zahlen
- Multiplikative Beharrlichkeit
- k-Permutationen
- Quasibefreundete Zahlen
- Zeckendorf-Zerlegung
- Gray-Code
- Biquadratische Quadrupel
- Abundante und defiziente Zahlen
Zahlentheorie - Natürliche Zahlen - Ganze Zahlen - Gebrochene Zahlen - Rationale Zahlen - Reelle Zahlen - Komplexe Zahlen - Zahlenbereiche- Definitionen - Zahlenmengen - Zuordnung - Zahlen zuordnen - Bezeichnungen - Übersicht
Die Zahlentheorie ist ein Themengebiet der Mathematik, welches sich mit den Eigenschaften von Zahlen und Zahlbereichen auseinandersetzt.
Zahlenbereiche werden als Mengen aufgefasst. Diese gliedern sich im Wesentlichen in die folgenden Zahlenarten: natürliche Zahlen, ganze Zahlen, rationale Zahlen, gebrochene Zahlen, reelle Zahlen, komplexe Zahlen und Kardinalzahlen.
Zahlenmengen umfassen eine definierte Menge an Zahlen, mit denen Berechnungen durchgeführt werden können.
Zahlbereichserweiterung: Unter einer Zahlbereichserweiterung wird die Konstruktion einer neuen Zahlenmenge aus einer gegebenen Zahlenmenge verstanden. Zahlbereichserweiterungen sind erforderlich, wenn bestimmte Rechenoperationen innerhalb eines Zahlenbereichs nicht mehr durchführbar sind.
Nachfolgend aufgeführt finden Sie eine Übersicht über die wichtigsten mathematisch definierten Zahlenbereiche bzw. Zahlenmengen.

Abb. 1: Zahlenbereiche
Aus dem zuvor Beschriebenen und dem gezeigten Mengendiagramm lassen sich folgende Zusammenhänge erkennen:
- Alle ganzen Zahlen sind rationale Zahlen
- Alle natürlichen Zahlen sind ganze Zahlen
- Alle rationalen Zahlen sind reelle Zahlen
- Alle irrationalen Zahlen sind reelle Zahlen
- Die Menge der reellen Zahlen bildet sich aus der Menge der rationalen Zahlen und der Menge der irrationalen Zahlen

Abb. 2: Zahlenbereiche
ℕ: Natürliche Zahlen
ℤ: Ganze Zahlen
ℚ: Rationale Zahlen
ℝ: Reelle Zahlen
ℂ: Komplexe Zahlen
Im Folgenden wird auf die wichtigsten Zahlenarten und derern Eigenschaften eingegangen.
Natürliche Zahlen (Menge der natürlichen Zahlen):
Der Bereich der natürlichen Zahlen umfasst die Zahlen die zum Zählen von Gegenständen benötigt werden. Jede natürliche Zahl besitzt einen Nachfolger und somit eine Zahl, welche um eins größer ist als die entsprechende natürliche Zahl. Die natürlichen Zahlen lassen sich mit Hilfe der Ziffern 0, 1, 2, 3 ,4, 5, 6, 7, 8 und 9 darstellen. Sie sind eine Zeilmenge der ganzen Zahlen. Mit Hilfe einer Stellenschreibweise von rechts nach links lassen sich sämtliche Zahlen darstellen. Es existiert keine letzte natürliche Zahl.
Zahlen von 0 bis 9 belegen die Einerstelle. Zahlen von 10 bis 99 belegen die Einerstelle sowie die Zehnerstelle. Zahlen von 100 bis 999 belegen die Einerstelle, die Zehnerstelle sowie die Hunderterstelle usw.

Symbol: ℕ
Beispiele: 1, 2, 3, 4, 12, 1299, 567778, 50883995678676741
Ganze Zahlen (Menge der ganzen Zahlen):
Alle Differenzen (a-b) aus den geordneten Paaren {a,b} natürlicher Zahlen, die dem selben Punkt der Zahlengeraden zugeordnet sind, gehören zur gleichen Klasse und heißen ganze Zahl. Durch die Festlegung der Zahl 0 als Bezugspunkt besteht die Möglichkeit unendlich große sowie unendlich kleine Zahlen zu bilden.
Symbol: G
Beispiele: -6, -5, -1, 0, 2, 4, 7, 13
Rationale Zahlen (Menge der rationalen Zahlen):
Rationale Zahlen sind Klassen von Quotienten, die Punkten auf der reellen Zahlengerade entsprechen. Sie haben weder Vorgänger noch Nachfolger. Zwischen zwei rationalen Zahlen liegen beliebig viele weitere rationale Zahlen.
Symbol: ℚ
Beispiele: -1, -3/4, -1/9, 1, 3/7, 4/19
Positive rationale Zahlen bilden die Menge Q+.
Negative rationale Zahlen bilden die Menge Q−.
Gebrochene Zahlen (Menge der gebrochenen Zahlen):
Gebrochene Zahlen sind eine Erweiterung der natürlichen Zahlen, welche es gestattet die Addition, Multiplikation und die Division uneingeschränkt auszuführen. Die Subtraktion zweier Zahlen dieser Art liefert lediglich dann wieder einen Bruch, wenn der Subtrahend kleiner oder gleich dem Minuend ist.
Symbol: ℚ+
Beispiele: 1, 4/9, 8/23
Reelle Zahlen (Menge der rellen Zahlen - Reeller Zahlenbereich):
Eine reelle Zahl ist ein unendlicher Dezimalbruch. Dieser stellt als Folge von Gliedern ineinander geschachtelte Intervalle jeweils gleicher Teile dar. Die reelle Zahl liegt auf dem Zahlenstrahl in all diesen Intervallen. Zahlen dieser Art werden eineindeutig auf die reelle Zahlengerade abgebildet. Der reelle Zahlenbereich beinhaltet alle Wurzeln nichtnegativer Zahlen. Er enthält alle unendlichen nicht periodischen Dezimalbrüche.
Symbol: R
Beispiele: -√3, √7, Pi
Positive reelle Zahlen bilden die Menge R+.
Negative reelle Zahlen bilden die Menge R−.
Komplexe Zahlen (Menge der komplexen Zahlen):
Eine komplexe Zahl hat die Form z = a + jb mit a,b ∈ R und j2 = -1. Jede komplexe Zahl setzt sich aus einer reellen sowie einer imaginären Einheit zusammen. Die Menge der komplexen Zahlen C bildet sich aus der Menge aller Zahlen a +b·j. Sie kann durch Punkte auf der imaginären Zahlengerade als Vielfaches der imaginären Einheit j dargestellt werden.
Symbol: ℂ
Beispiele: i, -2i, 4 + 6i, 15 - 4i
Grundzahl (Kardinalzahl):
Grundzahlen (Kardinalzahlen oder natürliche Zahlen) sind positive ganze Zahlen, welche die Grundlage zur Zählung von Größen bilden. Sie bezeichnen eine Menge oder eine Anzahl.
Transzendente Zahlen:
Bei transzendenten Zahlen handelt es sich um irrationale Zahlen, die nicht in Form eines Polynoms darstellbar sind. Beispiele für Zahlen dieser Art sind die Eulersche Zahl e = 2,71828, die Kreiszahl π = 3,14159 oder die Werte von sin(35°) = 0,57357 bzw. tan(40°) = 0,83909.
Negative Zahlen - Positive Zahlen:
Im System der reellen Zahlen ist eine negative Zahl eine Zahl, die kleiner als Null ist und eine positive Zahl ist eine Zahl, die größer als Null ist.
Negative Dezimalzahl - Positive Dezimalzahl:
Negative Dezimalzahlen sind Kommazahlen die sich aus ihren Vorkommastellen, dem Komma sowie den Nachkommastellen zusammensetzen und kleiner als Null sind. Positive Dezimalzahlen sind Kommazahlen die sich aus ihren Vorkommastellen, dem Komma sowie den Nachkommastellen zusammensetzen und größer als Null sind.
Vollkommene Zahlen:
Als vollkommene Zahl wird eine Zahl bezeichnet, die gleich der Summe ihrer echten Teiler ist. Die ersten vollkommenen Zahlen sind 6, 28, 496 und 81268.
Rechenregeln zur Durchführung der Multiplikation und der Division von rationalen Zahlen:
- Besitzen beide zu multiplizierenden oder zu dividierenden Zahlen ein positves Vorzeichen, so ist auch das Ergebnis der durchgeführten Rechenoperation positiv. Es gilt: Plus mal plus ist plus
- Besitzen beide zu multiplizierenden oder zu dividierenden Zahlen ein negatives Vorzeichen, so ist das Ergebnis der durchgeführten Rechenoperation positiv. Es gilt: Minus mal minus ist plus
- Besitzt eine der beiden zu multiplizierenden oder zu dividierenden Zahlen ein positves Vorzeichen und die andere ein negatives Vorzeichnen, so ist das Ergebnis der durchgeführten Rechenoperation negativ. Es gilt: Plus mal minus ist minus und minus mal plus ist minus
Quersumme - Alternierende Quersumme - Quersummenregel - Wechselsumme - Ziffernsumme - Definitionen
Als Quersumme oder Ziffernsumme wird die Summe der Ziffernwerte einer natürlichen Zahl bezeichnet. Eine einstellige Quersumme (iterierte Quersumme) wird gebildet, indem die Berechnung der Quersumme der gebildeten Quersumme so lange erfolgt, bis diese lediglich noch einstellig ist.
Eine alternierende Quersumme wird gebildet, indem die Ziffern einer Zahl abwechselnd subtrahiert und addiert werden. Hierbei kann linksseitig oder rechtsseitig begonnen werden.
Beispiele für alternierende Quersummen:
q'(12345) = 4-3+2-1+5 = 7
q'(54321) = 1-2+3-4+5 = 3
q'(4124) = 4-1+2-4 = 1
Als Quersummenregel wird die Teilbarkeitsregel bezeichnet, die mittels der Quersumme einer Zahl über deren Teilbarkeit durch eine andere Zahl entscheidet.
Die Quersummenregel der Zahl 3 erteilt Auskunft darüber, dass eine Zahl durch 3 teilbar ist, wenn deren Quersumme durch die Zahl 3 ohne Rest teilbar ist.
Die Quersummenregel der Zahl 6 erteilt Auskunft darüber, dass eine Zahl durch 6 teilbar ist, wenn deren Quersumme durch die Zahl 6 ohne Rest teilbar ist.
Beispiele zur Quersummenregel:
64 233 ist durch die Zahl 3 teilbar, denn 6 + 4 + 2 + 3 + 3 = 18 und die Zahl 18 ist ohne Rest durch 3 teilbar (18:3 = 6).
76068 ist durch 9 ohne Rest teilbar, da die Quersumme 7 + 6 + 0 + 6 + 8 = 27 und die Zahl 27 ist ohne Rest durch 9 teilbar (27:3 = 9).
1138 ist nicht durch 3 teilbar, denn 1 + 1 + 3 + 8 = 13 und die Zahl 13 ist nicht durch 3 ohne Rest teilbar (13 : 3 = 4 Rest 1).
Neutrales Element
Zu verschiedenen Rechenoperationen existieren sogenannte neutrale Elemente. Ein neutrales Element verändert die ursprüngliche Zahl (die ursprüngliche Sache) hierdurch nicht.
Beispiele zu neutralen Elementen:
Wird zu einer Zahl die Zahl 0 addiert, so ändert sich die Sache (die Zahl) nicht. In diesem Fall ist die Zahl 0 das neutrale Element der Addition.
Wird die Multiplikation einer Zahl mit der Zahl 1 durchgeführt, so ändert sich die Sache (die Zahl) nicht. In diesem Fall ist die Zahl 1 das neutrale Element der Multiplikation.
Wird eine Vektoraddition mit einem Nullvektor durchgeführt, so ist der Nullvektor das neutrale Element.
Programmbedienung
Im Folgenden wird auf die einzelnen in diesem Modul zur Verfügung stehenden Module eingegangen und die erforderliche Bedienung des Programms beschrieben.
1. Partitionen
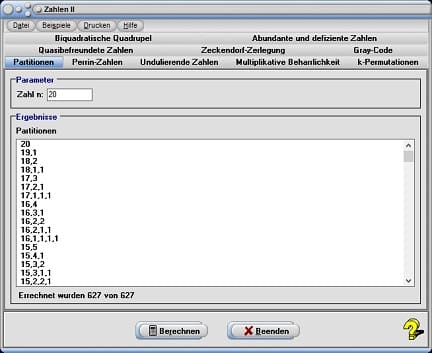
Unter der Partition einer natürlichen Zahl versteht man die Anzahl der Zerlegungen dieser Zahl in eine Anzahl von Summanden ≥ 1, wobei von derer Reihenfolge abgesehen wird.
Nach der Wahl des Registerblatts Partitionen, der Eingabe der zu zerlegenden Zahl in das Feld mit der Bezeichnung Zahl n und der Bedienung der Schaltfläche Berechnen listet das Programm die Kombinationen aller möglichen Zerlegungen in der Tabelle auf.
Bei der Zahl 100 sind bereits 190.569.292 verschiedene Zerlegungen möglich. Die Mathematiker Hardy und Ramanujan bewiesen 1918 mit analytischen Methoden ihre berühmte Partitionen-Formel, wonach sich die Anzahl der Möglichkeiten mit
p(n) ~1/(4n√3)epi√(2n/3) (n → ∞)
abschätzen lässt.
2. Perrin-Zahlen
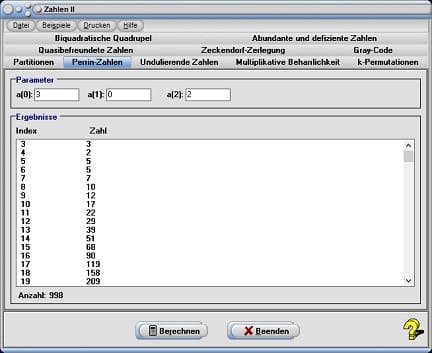
Die Perrin-Folge ist eine algebraische Zahlenfolge. Sie ist ähnlich der Fibonacci-Folge eine rekursive Folge, bei welcher ein Glied dieser Folge die Summe von Vorgängergliedern ist.
Die Glieder der Perrin-Folge werden wie folgt definiert:
a0 = 3
a1 = 0
a2 = 2
an = an-2 + an-3
Hieraus ergeben sich für die ersten Glieder der Folge die Zahlen:
3, 0, 2, 3, 2, 5, 5, 7, 10, 12, 17, 22, 29, 39, 51, 68, 90, ...
Mit Ausnahme von n = 1 sind alle n, welche a(n) restlos teilen, Primzahlen. Diesen Sachverhalt können Sie analysieren, indem Sie nach der Wahl des Registerblatts Perrin-Zahlen die Anfangsglieder für die Folge in den Eingabefeldern a(0), a(1), sowie a(2) mit den o.a. Werten definieren und hiernach die Schaltfläche Berechnen bedienen. Das Programm gibt hierauf die weiteren Glieder der Folge in der Tabelle aus. Durch die Eingabe entsprechender Werte können andere Folgen analysiert werden. Eine Padovan-Folge ergibt sich mit den Anfangsgliedern a(0) = 1, a(1) = 1 und a(2) = 1.
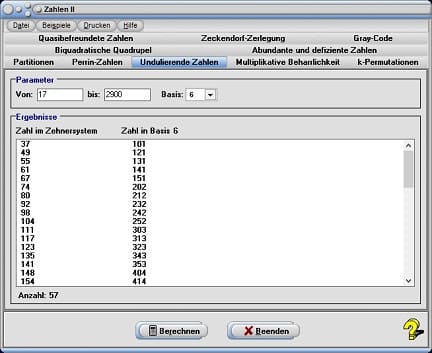
3. Undulierende Zahlen
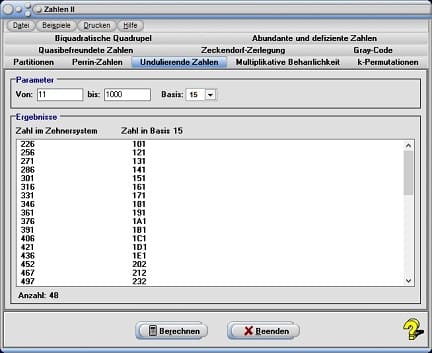
Als undulierende Zahlen werden Zahlen bezeichnet, deren Werte einzelner Ziffern in deren Folge abwechselnd steigen und fallen. Wird das Registerblatt Undulierende Zahlen gewählt, so bietet das Programm die Möglichkeit, derartige Zahlen verschiedener Zahlensysteme ermitteln zu lassen.
Legen Sie den Bereich über den derartige Zahlen ausgegeben werden sollen, durch Eingabe entsprechender ganzzahliger Werte (im Zehnersystem) in die Felder von und bis fest. Selektieren Sie aus der aufklappbaren Auswahlbox Basis die Basis des Zahlensystems für welche die Auswertung durchgeführt werden soll und bedienen Sie hierauf die Schaltfläche Berechnen. Das Programm sucht nach Zahlen die im gewählten Zahlensystem undulierend sind und gibt diese in der rechten Spalte der Tabelle aus. In derer linken Spalte werden die entsprechenden Dezimalzahlen aufgelistet.
Beispiel
Soll eine Suche nach undulierenden Zahlen im Dualsystem durchgeführt werden, so ermittelt das Programm innerhalb des festgelegten Untersuchungsbereichs für Zahlen (im Dezimalsystem) von 11 - 1000 folgende undulierende Zahlen für das System mit der Basis 2:
| Dezimal | Basis 2 |
| 21 | 10101 |
| 42 | 101010 |
| 85 | 1010101 |
| 170 | 10101010 |
| 341 | 101010101 |
| 682 | 1010101010 |
4. Multiplikative Beharrlichkeit
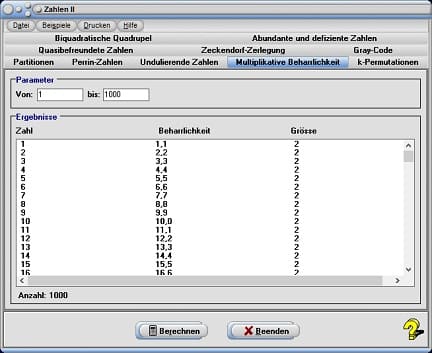
Man nehme eine natürliche Zahl und bilde das Produkt ihrer Ziffern. Dies wird solange (falls möglich) mit der resultierenden Zahl wiederholt, bis man bei einer einstelligen Zahl angelangt ist.
Die Anzahl der Schritte wird multiplikative Beharrlichkeit der Ausgangszahl genannt. Zehn ist die kleinste natürliche Zahl, deren multiplikative Beharrlichkeit gleich 1 ist. Zu den Werten 2-6 gehören folgende Zahlen: 24, 29, 75, 17117, 67671.
Die kleinste Zahl mit der multiplikativen Beharrlichkeit 11 lautet: 277 777 788 888 899. Es gibt keine Zahl kleiner als 1050, deren multiplikative Beharrlichkeit größer als 11 ist. Es wird angenommen, dass es für die multiplikative Beharrlichkeit der natürlichen Zahlen eine Obergrenze gibt.
Wählen Sie das Registerblatt Multiplikative Beharrlichkeit, so werden die Beharrlichkeiten natürlicher Zahlen ermittelt, nachdem Sie die den Bereich zu untersuchender Zahlen durch die Eingabe von Werten in die Felder von und bis definieren und anschließend die Schaltfläche Berechnen bedienen.
Beispiel
Möchten Sie die Beharrlichkeit der Zahl 86 ermitteln lassen, so geben Sie die Werte 86 in beide Felder ein.
Das Programm gibt hierauf die Zeichenfolge 86, 48, 32, 6 aus, denn:
8·6 = 48
4·8 = 32
3·2 = 6
5. k-Permutationen
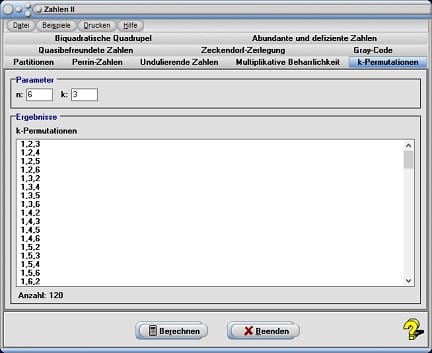
Eine Wahl des Registerblatts k-Permutationen ermöglicht die Ermittlung der Kombinationen bei Durchführung einer k-Permutation.
Teilmengen einer Gesamtmenge n können in n! / (n-k)! verschiedenen Reihenfolgen angeordnet werden. Nach Festlegung der Zahlen für die Gesamtmenge n im Eingabefeld n, der Anzahl der Teilmengen im Eingabefeld k und einer Bedienung der Schaltfläche Berechnen ermittelt das Programm alle möglichen Kombinationen (Anordnungen) dieser und gibt die Ergebnisse in einer Tabelle aus.
Wurde für k ein Wert > n-1 eingegeben, so erhalten Sie eine Fehlermeldung. Ist der Eingabewert für k größer 10, so verwendet das Programm den Wert 10.
6. Quasibefreundete Zahlen
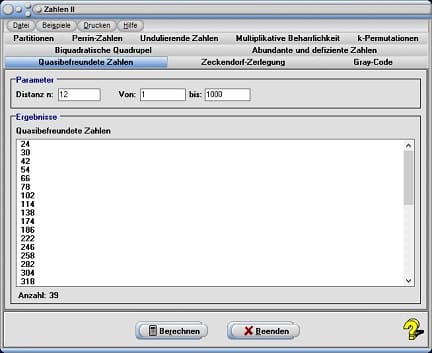
Zwei natürliche Zahlen heißen befreundet, wenn jede dieser Zahlen gleich der Summe der echten Teiler der anderen Zahl ist (unter Einbeziehung der Zahl 1). Das kleinste Paar befreundeter Zahlen ist 220 und 284.
Die Teilersumme von 220 ist:
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
Die Teilersumme von 284 ist:
1 + 2 + 4 + 71 + 142 = 220
Als quasibefreundeten Zahlen werden Zahlen bezeichnet, für welche gilt:
σ(a) = σ(b) = a + b + 1.
wobei
σ(a): Summe der Teiler der Zahl a (ohne die Zahl a)
σ(b): Summe der Teiler der Zahl b
Die Untersuchung der Eigenschaften natürlicher Zahlen kann ausgeweitet werden auf Zahlen, die folgende Bedingung zu sich selbst erfüllen:
σ(a) = σ(b) = a + b + n
σ(a): Summe der Teiler der Zahl a (ohne die Zahl a)
σ(b): Summe der Teiler der Zahl b
n: beliebige ganze Zahl
Hiernach kann in diesem Unterprogramm gesucht werden. Wählen Sie hierfür das Registerblatt Quasibefreundete Zahlen. Geben Sie zunächst die Zahl n in das Feld mit der Beschriftung Distanz n ein. Legen Sie hierauf den zu untersuchenden Wertebereich durch Eingabe der entsprechenden Zahlen in die Felder von und bis fest. Bedienen Sie die Schaltfläche Berechnen, so gibt das Programm, zu sich selbst quasibefreundete Zahlen, in der Tabelle aus.
Beispiel
Die Summe der Teiler der Zahl 102 (ohne sich selbst) beträgt 114. Da die Summe der Zahl 102 und der Zahl 12 ebenso 114 ergibt, ist die gesuchte Zahl die Zahl 102.
7. Zeckendorf-Zerlegung
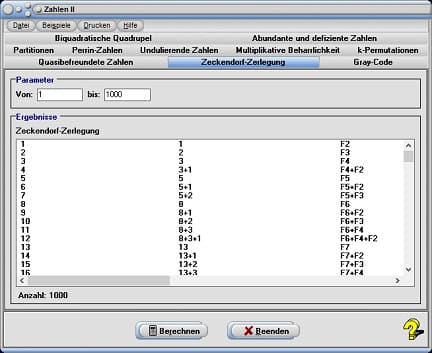
Das Zeckendorf-Theorem besagt, dass jede natürliche Zahl n größer Null eindeutig als Summe voneinander verschiedener, nicht direkt aufeinanderfolgender Fibonacci-Zahlen geschrieben werden kann.
In diesem Unterprogramm können Sie die Zeckendorf-Zerlegung natürlicher Zahlen durchführen lassen. Wählen Sie hierzu das Registerblatt Zeckendorf-Zerlegung und legen Sie den Intervallbereich zu zerlegender Zahlen, durch Eingabe der Werte in die Felder von und bis fest. Bedienen Sie hierauf die Schaltfläche Berechnen, so gibt das Programm die entsprechenden Sequenzen aus.
Diese Zerlegung kann in Form einer Dualzahl geschrieben werden. Enthält die Zerlegung eine Fibonacci-Zahl mit der Indexnummer n, so erhält die Dualzahl an Stelle n eine 1, andernfalls eine 0. Begonnen wird mit der Indexnummer der größten Fibonacci-Zahl.
In den Tabellenspalten wird Folgendes ausgegeben:
| Spalte 1: | Zu zerlegende Zahl z |
| Spalte 2: | Summe der Fibonacci-Zahlen, deren Summe die Zahl z ergibt |
| Spalte 3: | Indexnummern der Fibonacci-Zahlen, deren Summe die Zahl z ergibt |
| Spalte 4: | Dualschreibweise der Zerlegung |
Beispiel
Die Zeckendorf-Zerlegung der Zahl 30 ergibt:
21 + 8 + 1
F8 + F6 + F2
10100010
Dies bedeutet:
Die Zahl 30 lässt sich in die Summe der Fibonacci-Zahlen 21, 8 und 1 zerlegen. Deren Indexnummern sind F2, F6 und F8. In Form einer Folge der Zahlen 0 und 1 ausgedrückt, lautet die Folge der Fibonacci-Indexnummern 10100010. Aufgrund der Tatsache, dass die größte Fibonacci-Indexnummer den Wert 8 besitzt, ist die Folge 8 Zeichen lang. Da die Fibonacci-Zahl 8 (F8) vorkommt, besitzt die duale Darstellung der Zeckendorf-Zerlegung an Stelle 1 den Wert 1. Da Fibonacci-Zahl 7 (F7) nicht vorkommt, ist Stelle 2 mit einer 0 belegt. Stelle 3 erhält den Binärwert 1, da Fibonacci-Zahl 6 (F6) vorhanden ist, usw..
8. Gray-Code
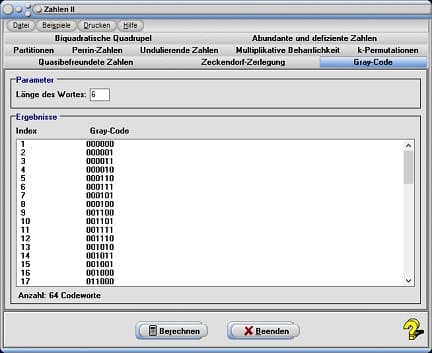
Der Gray-Code (nach dem Physiker Frank Gray) ist ein stetiger binärer Code, bei welchem sich benachbarte Codewörter exakt in einer einzigen dualen Ziffer unterscheiden.
Der Gray-Code ist nicht nur einschrittig, sondern auch zyklisch. Dies bedeutet: Erweitert man ihn auf alle 16 Tetraden, folgen alle Tetraden derart aufeinander, dass sich beim Übergang der letzten Tetrade, 1510 = 1000 auf die erste Tetrade 010 = 0000, wieder nur ein Bit ändert. Daraus folgt, dass der erweiterte Gray-Code zyklisch ist. Beim unerweiterten Gray-Code ändern sich beim Übergang von 1010 auf 010 drei Tetraden. Somit ist der unerweiterte Gray-Code nicht zyklisch.
Codierungstabelle des nicht zyklischen Gray-Codes:
| Dezimal | Gray-Code | |||
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 1 |
| 3 | 0 | 0 | 1 | 0 |
| 4 | 0 | 1 | 1 | 0 |
| 5 | 0 | 1 | 1 | 1 |
| 6 | 0 | 1 | 0 | 1 |
| 7 | 0 | 1 | 0 | 0 |
| 8 | 1 | 1 | 0 | 0 |
| 9 | 1 | 1 | 0 | 1 |
Codierungstabelle des zyklischen Gray-Codes:
| Dezimal | Gray-Code | |||
| 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 1 |
| 3 | 0 | 0 | 1 | 0 |
| 4 | 0 | 1 | 1 | 0 |
| 5 | 0 | 1 | 1 | 1 |
| 6 | 0 | 1 | 0 | 1 |
| 7 | 0 | 1 | 0 | 0 |
| 8 | 1 | 1 | 0 | 0 |
| 9 | 1 | 1 | 0 | 1 |
| 10 | 1 | 1 | 1 | 1 |
| 11 | 1 | 1 | 1 | 0 |
| 12 | 1 | 0 | 1 | 0 |
| 13 | 1 | 0 | 1 | 1 |
| 14 | 1 | 0 | 0 | 1 |
| 15 | 1 | 0 | 0 | 0 |
Näheres siehe Fachliteratur.
Wählen Sie das Registerblatt Gray-Code, geben Sie in das Feld Länge des Wortes die entsprechende Wortlänge ein und bedienen Sie die Schaltfläche Berechnen, so werden die entsprechenden Codes ausgegeben.
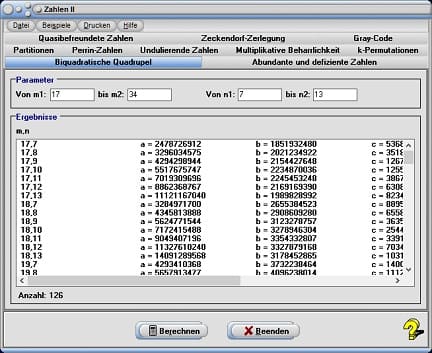
9. Biquadratische Quadrupel

Biquadratische Quadrupel sind die Quadrupel natürlicher Zahlen a, b, c und d, die die Bedingungen a4 + b4 = c4 + d4 erfüllen. Diese können Sie ermitteln lassen, indem Sie das Registerblatt Biquadratische Quadrupel wählen.
Für deren Lösungen ergeben sich:
a = v + w
b = t - u
c = v – w
d = t + u
mit:
t = 2n (4m6+m4n²+10m²n4+n6)
u = m (-m4+18m²n²-n4) (m²+n²)
v = n (-m4+18m²n²-n4) (m²+n²)
w = 2m (m6+10m4n²+m²n4+4n6)
wobei n und m positive, natürliche Zahlen sind.
Geben Sie die Parameterwerte für m und n in die Felder von m1, bis m2, von n1 und bis n2 ein. Bedienen Sie hierauf die Schaltfläche Berechnen, so werden die Lösungen für die Parameter der Gleichungen in der Tabelle ausgegeben.
Beispiel
Bei Festlegung der Wertebereiche von m1 = 1 bis m2 = 2, sowie n1 = 1 bis n2 = 2 erhalten Sie für die Parameter m = 1 und n = 2 die Lösungen:
a = 1203
b = 76
c = 653
d = 1176
Die Gleichung 12034 + 76b4 = 6534 + 11764 erfüllt die Bedingung a4 + b4 = c4 + d4.
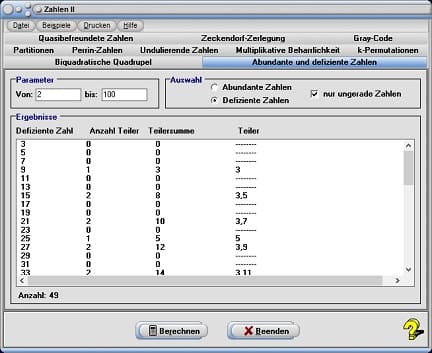
10. Abundante und defiziente Zahlen
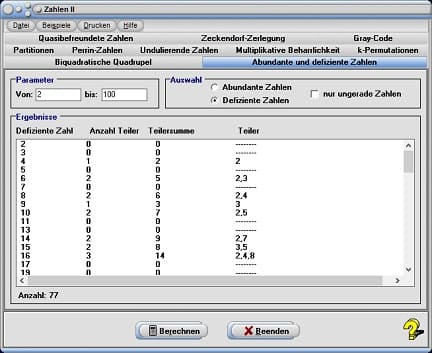
Die Summe der echten Teiler einer natürlichen Zahl n ist die Summe der Teiler von n, ohne die Zahl n selbst und wird bezeichnet mit σ*(n).
Eine natürliche Zahl n > 1 heißt:
vollkommen (vollkommene Zahl), wenn σ*(n) = n
defizient oder teilerarm (defiziente Zahl), wenn σ*(n) < n
abundant oder teilerreich (abundante Zahl), wenn σ*(n) > n
In diesem Unterprogramm, welches durch die Wahl des Registerblatts Abundante und defiziente Zahlen aufgerufen werden kann, können abundante und defiziente Zahlen ermittelt werden.
Wurde der Kontrollschalter Abundante Zahlen aktiviert, so gibt das Programm alle abundanten Zahlen innerhalb eines Wertebereichs aus, der durch die Eingabe von Zahlenwerten in die Felder von sowie bis festgelegt wurde. Nach einer Aktivierung des Kontrollschalters Defiziente Zahlen geschieht dies für defiziente Zahlen. Durchgeführt wird eine Untersuchung nachdem der Kontrollschalter Berechnen bedient wurde. Die Ergebnisse werden in der hierfür zur Verfügung stehenden Tabelle ausgegeben. Eine vorherige Aktivierung des Kontrollkästchens nur ungerade Zahlen veranlasst das Programm die Untersuchungen nur mit ungeraden, natürlichen Zahlen durchzuführen.
Außer den abundanten bzw. defizienten Zahlen gibt das Programm noch deren ganzzahlige Teiler, die Teilersumme dieser, sowie deren Anzahl aus.
Beispiel
Da die Anzahl der Teiler (2, 4, 5 und 10) der Zahl 20 kleiner als deren Teilersumme ist, wird diese als abundante Zahl ausgegeben. Die Zahl 6, deren Teiler die Zahlen 2 und 3 sind und deren Teilersumme 5 beträgt, wird als defiziente Zahl ermittelt.
Allgemeiner Hinweis zu diesem Modul
Hinweis:
Da die Durchführung einiger Berechnungen sehr zeitaufwändig sein kann, können Sie diese jederzeit durch einmaliges Drücken der Taste ESC abbrechen.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Weitere Themenbereiche

Beispiel 1

Beispiel 2
Beispiel 3
Beispiel 4
Beispiel 5
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.
Wikipedia - Perrin-Folge
Wikipedia - Undulierende Zahl
Wikipedia - Permutation
Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte
MathProf 5.0 - Unterprogramm Zahlen I

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















