MathProf - Winkel - Dreieck - Wechselwinkel - Nebenwinkel - Summe

Modul Winkel am Dreieck

---

 
Das Programmmodul [Trigonometrie] - [Dreieckswinkel] - Winkel am Dreieck ist implementiert, um sich die Zusammenhänge bzgl. Winkelverhältnissen am Dreieck verdeutlichen zu können.

 

In diesem Unterprogramm besteht die Möglichkeit, Winkelverhältnisse am Dreieck zu untersuchen. Es ermöglicht die Durchführung der Winkelberechnung der Innenwinkel eines Dreiecks. Als Winkelverhältnis wird bei einer geometrischen Figur das Verhältnis zweier Seiten hinsichtlich der Winkel, die von ihnen gebildet werden, bezeichnet.
 

Grundsätzlich gilt es bezüglich des zuvor Geschilderten folgende Zusammenhänge zu beachten:
 

• Die Summe aller Nebenwinkel und Wechselwinkel am Dreieck muss 180° betragen (Innenwinkelsumme - Winkelsumme des Dreiecks).
• Die Summe der Innenwinkel eines Dreiecks muss 180° betragen (Innenwinkelsumme - Winkelsumme des Dreiecks).
• Stufenwinkel und entgegengesetzte Winkel am Dreieck müssen gleich groß sein.

Eine Winkelberechnung wird zur Bestimmung des Werts eines Winkels ausgeführt. Dieses Modul ermöglicht die statische sowie die interaktive Durchführung von Winkelberechnungen bezüglich Nebenwinkeln, Wechselwinkeln und Stufenwinkeln beim Dreieck.

---

Die Winkel auf der Innenseite eines Dreiecks werden als Innenwinkel bezeichnet. Die Innenwinkel eines Dreiecks sind diejenigen Winkel, deren Scheitelpunkte die Ecken des Dreiecks sind. Die Innenwinkelsumme (Winkelsumme) einer ebenen geometrischen Figur entspricht der Summe aller Innenwinkel dieser.
 
Nebenwinkel liegen auf einer Gerade nebeneinander. Zwei Winkel sind Nebenwinkel, wenn sie an der Kreuzung einer Geraden beisammen liegen.

Wechselwinkel und Stufenwinkel enstehen, wenn zwei Parallelen von einer Geraden geschnitten werden.

Als Außenwinkel eines Dreiecks werden Winkel bezeichnet, die sich an einem Eckpunkt dessen außen ergeben, wenn eine Seite des Dreiecks verlängert wird.

Als Gegenwinkel oder Scheitelwinkel wird das Paar gegenüberliegender Winkel bezeichnet die entstehen, wenn zwei Geraden sich schneiden.

Als Winkelpaar wird ein Paar zweier Winkel bezeichnet, deren Eigenschaften sich durch ihre gegenseitige Lage hervorrufen.

   
Als Winkelsatz wird eine Aussage oder Regel bezeichnet, die über Winkel an den Schnittpunkten von wenigstens zwei Geraden Auskunft erteilt. Nachfolgend sind Winkelsätze aufgeführt. Sie beschreiben Regeln hinsichtlich der Größe von Winkeln, welche bei den Schnittpunkten zweier Geraden auftreten.
 
Nebenwinkelsatz:

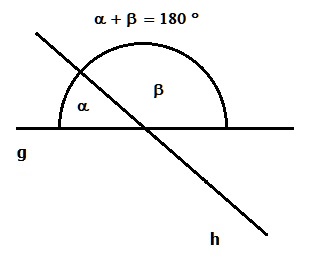
Der Nebenwinkelsatz besagt, dass sich Nebenwinkel zu 180° ergänzen. Es gilt:

α + α′ = 180°
β + β′ = 180°
γ + γ′ = 180°

Innenwinkelsatz:

Der Innenwinkelsatz besagt, dass die Summe aller Innenwinkel in einem Dreieck 180° beträgt.

α + β + γ = 180°

Außenwinkelsatz:

Der Außenwinkelsatz besagt, dass der Außenwinkel an einer Ecke eines Dreiecks stets gleich der Summe der Innenwinkel an den beiden anderen Ecken dessen entspricht.

Wechselwinkelsatz:

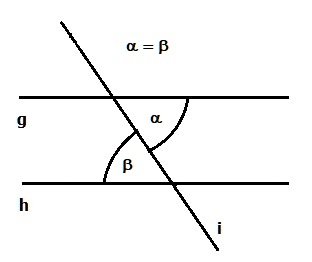
Der Wechselwinkelsatz besagt, dass Wechselwinkel genau dann gleich groß sind, wenn sie an parallelen Geraden liegen.

Stufenwinkelsatz:

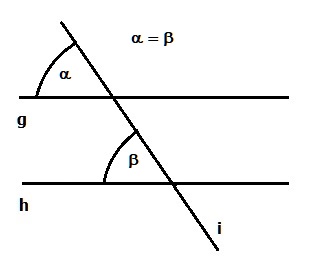
Der Stufenwinkelsatz besagt, dass Stufenwinkel genau dann gleich groß sind, wenn sie an parallelen Geraden liegen.
 
 

 
Grafisch darstellen lassen können Sie sich die Winkelverhältnisse am Dreieck in diesem Modul, wenn Sie Folgendes ausführen:
 

1. Geben Sie die Werte für exakt zwei Winkel in dafür zur Verfügung stehende Felder ein. Bedienen Sie ggf. zuvor die Schaltfläche Löschen.
    
2. Klicken Sie hierauf auf die Schaltfläche Darstellen. Sind mit den Eingabewerten Berechnungen durchführbar, so wird die grafische Darstellung ausgegeben. Nachdem diese beendet wird, werden die ermittelten Ergebnisse zudem in den Eingabefeldern des Hauptfensters des Unterprogramms angezeigt.

 
Bei Ausgabe der grafischen Darstellung stellt das Programm die Zusammenhänge dar, welche durch Eingabewerte ermittelt wurden. Es wird jedoch zusätzlich die Möglichkeit geboten, die Lage des Punktes C mit der Maus zu verändern und somit weitere Untersuchungen durchzuführen. Klicken Sie in diesem Fall mit der linken Maustaste in den rechteckig umrahmten Mausfangbereich dieses Punktes und bewegen Sie den Mauscursor bei gedrückt gehaltener Maustaste. Wird diese Option benutzt, so werden Eingabewerte und ermittelte Winkelwerte, welche nach Beendigung der Ausgabe der grafischen Darstellung vorgabemäßig in den Eingabefeldern dieses Unterprogramms ausgegeben werden, hierauf jedoch gelöscht.

 
Hinweis:

Um sich detaillierte Informationen bzgl. der Eigenschaften des Dreiecks ABC ausgeben zu lassen, wählen Sie den Menüpunkt Datei - Dreieckseigenschaften. Hierauf erscheint ein Ausgabefenster mit den relevanten Daten. Um diese im *.txt-Format zu speichern, verwenden Sie den dort vorhandenden Menüeintrag Datei - Ergebnisse speichern.
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Grafikprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Üben sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Benutzbarbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Übungen hierzu. Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens genutzt werden.
 
Oftmals lassen sich hiermit auch die Lösungen von Übungsaufgaben durch benutzerdefinierte Festlegungen und Eingaben numerisch oder grafisch ermitteln bzw. auswerten. Erlernte Fertigkeiten können somit auf anschauliche Weise untersucht werden. Implementierte Beispiele zu Sachverhalten erlauben die Bezugnahme zum entsprechenden Fachthemengebiet.

Mittels der anschaulichen Gestaltung und leichten Bedienbarbarkeit der einzelnen Module dieser Software werden oftmals häufig gestellte Fragen mit den Anfangsworten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? zum entsprechenden Themengebiet auf verständliche Weise beantwortet und einfach erklärt sich durch dessen Benutzung vieles von alleine. Zudem liefert diese Applikation zu vielen gestellten Fragen eine verständliche Antwort, Beschreibung und Erklärung.

 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

 

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:

• Punkte beschriften: Beschriftung des Mausfangpunktes und der Eckpunkte des Dreiecks ein-/ausschalten
• Koordinaten: Anzeige der Koordinaten des Mausfangpunktes und der Eckpunkte des Dreiecks ein-/ausschalten
• Dreieck füllen: Farbfüllung der Dreiecksfläche ein-/ausschalten

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Innenwinkel des Dreiecks

Winkel am Kreis

Winkel an Parallelen
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3
    

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Innenwinkel zu finden.
 

Rechtwinkliges Dreieck - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck aus Seitenlängen und Winkeln - Allgemeines Dreieck durch 3 Punkte - Allgemeines Dreieck - Interaktiv - Satz des Pythagoras - Verallgemeinerung des Satz des Pythagoras - Satz des Thales - Höhensatz - Kathetensatz - Innenwinkel des Dreiecks - Winkel am Kreis - Winkel an Parallelen - Sinus und Cosinus am Einheitskreis - Tangens und Cotangens am Einheitskreis - Tangentendreieck - Höhenfußpunktdreieck - Lamoen-Kreis - Taylor-Kreis - Euler-Gerade - Simson-Gerade - Satz von Ceva - Isodynamische Punkte des Dreiecks - Isogonal konjugierte Punkte - Spieker-Punkt - Apollonius-Punkt
 

 

Startfenster des Unterprogramms Winkel am Dreieck
 

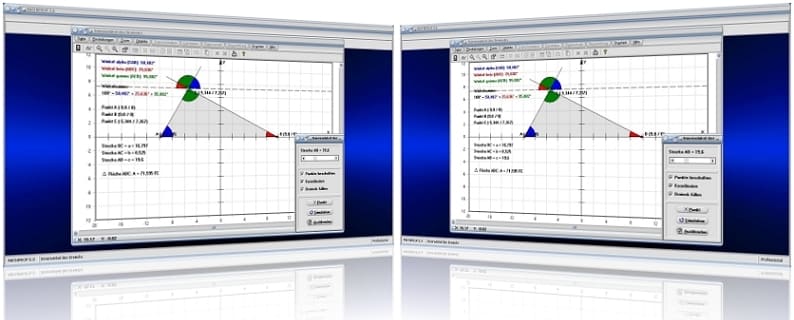
MathProf 5.0 - Unterprogramm Innenwinkel des Dreiecks

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

  

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---