MathProf - Tutorial zur Erweiterung zweidimensionaler Grafiken
Thema: Tutorial zur Erweiterung und Anpassung zweidimensionaler Grafiken
MathProf - Ein Programm zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.
Online-Hilfe
in Form eines Tutorials zur Erweiterung und Anpassung zweidimensionaler Grafiken.
Im Folgenden wird das Verfahren gezeigt, welches die Erweiterung der Darstellung eines Sachverhalts in einem Unterprogramm mit zweidimensionaler Grafikausgabe hinsichtlich deren Gestaltung ermöglicht.
Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.
Themen und Stichworte zu diesem Modul:Tutorial - Grafik erweitern - Anleitung - Gestaltung - Erweiterung - Anpassung - Anpassen - Vorgehen - Verfahren - Methode - Darstellung - 2D - Grafisch - Hintergrund - Bild - Layout - Kurve - Zusätzlich - Zusatz |
Tutorial zur Erweiterung zweidimensionaler Grafiken
Nachfolgend beschrieben finden Sie ein kleines Schnell-Einstiegs-Tutorial, in welchem gezeigt werden soll, welche Möglichkeiten im Programm bei der Ausgabe zweidimensionaler grafischer Darstellungen geboten werden, um mit Hilfe der hierbei zur Verfügung stehenden Methoden, Sachverhalte zu analysieren und grafisch aufzubereiten. Hierbei soll lediglich das Prinzip der erforderlichen Vorgehensweise anhand eines sehr einfachen, schnell und leicht nachvollziehbaren Beispiels aufgezeigt werden.
Schritt 1
Öffnen Sie das Unterprogramm Trigonometrie - Taylor-Kreis.
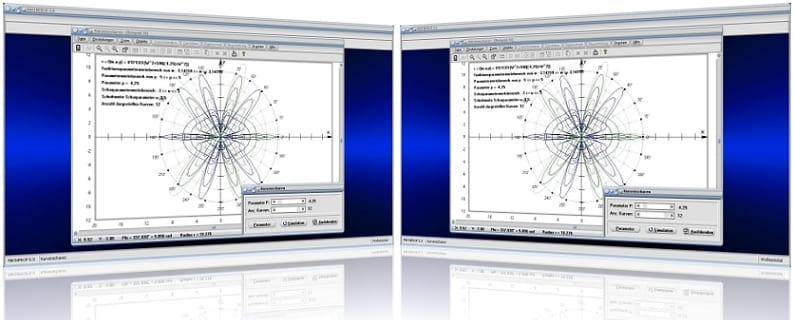
Es wird die oben gezeigte grafische Darstellung ausgegeben.
Schritt 2
Wählen Sie den Menüpunkt Objekte - Vieleck.
Geben Sie in das Feld Anzahl Ecken n die Zahl 8 ein, legen Sie im Feld Umkreisradius r den Wert 11,5 fest, belassen Sie alle anderen Einstellungen auf diesem Fenster auf Vorgaben und bedienen Sie die Schaltfläche Ok.
Das Programm stellt nun das erzeugte Objekt Vieleck V0 gemäß dem oben gezeigten Bild dar.
Schritt 3
Wählen Sie hierauf den Menüpunkt Datei - Kurve darstellen - in Polarform.
Es erscheint ein Fenster, auf welchem Sie den Funktionsterm der darzustellenden Kurve festlegen können. Geben Sie dort in das Feld r = f(w,p) = den Term
19/5*(COS(5*(W+PI/2)^2+P)^2*COS(5*(W+PI/2)^2+P)^2+2)
ein. Belassen Sie alle dort verfügbaren Einstellungen auf Vorgabewerten und bedienen Sie die Schaltfläche Ok, so stellt das Programm daraufhin die durch den festgelegten Term definierte Kurve r = f(φ,p) = 19/5·(cos(5·(φ+π/2)²+p)²·cos(5·(φ+π/2)²+p)²+2) über den Bereich -π ≤ φ ≤ π dar und blendet nachfolgend gezeigtes Bedienformular ein.
Bedienen Sie auf dem rechts unten angeordneten Fenster zur Konfiguration der Kurvendarstellung, die Schaltfläche Farbe und weisen Sie der Kurve die Farbe blau zu. Aktivieren Sie hierbei zudem das Kontrollkästchen Vorne.
Schritt 4
Wählen Sie nun den Menüpunkt Datei - Bild - Hintergrundbild laden (dynamisch) temporär und öffnen Sie die dem Programm beiliegende Datei Hintergrund_Tutorial.jpg. Diese befindet sich im lokalen Installationsorder des Programms im Unterordner Hintergrundbild.
Um die dargestellten Anfasser der erzeugten Vielecks auszublenden, wählen Sie den Menüpunkt Einstellungen - Objektanfasser - Alle Objektanfasser ausblenden. Die Anfasser des dargestellten Dreiecks blenden Sie aus, indem Sie den Menüpunkt Einstellungen - Alle Objektanfasser ausblenden wählen.
Schritt 5
Sind ggf. zusätzlich Freihandzeichnungen oder zusätzliche Texte auf dieser Darstellung aufzubringen, so aktivieren Sie den Menüpunkt Einstellungen - Zeichnen einschalten. Hierauf wird das linksbündig angedockte Tool zur Verfügung gestellt, mit welchem Zeichenoperationen ausgeführt werden können.
Im Bildformat speichern können Sie die erstellte Grafik, indem Sie den Menüpunkt Datei - Bild - Darstellung als Bild speichern wählen. Das implementierte Objekt (Vieleck) inkl. Hintergrundbild können Sie unter Datei - Objektdatei speichern sichern.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Weitere Themenbereiche
Tutorial zur Erweiterung zweidimensionaler Grafiken
Parameter
Lineare Auflösung
Nichtliineare Auflösung
Rahmen und Raster
Scrollen - Zoomen - Mausoperationen
MathProf 5.0 - Unterprogramm Kurvenscharen von Funktionen in Polarform
MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Physik interaktiv
Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
- Kurzinfos zum Themengebiet Mechanik
- Kurzinfos zum Themengebiet Elektrotechnik
- Kurzinfos zum Themengebiet Optik
- Kurzinfos zum Themengebiet Thermodynamik
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
