MathProf - Taschenrechner - Komplexe Zahlen - Imaginäre Zahlen

Fachthema: Taschenrechner für komplexe Zahlen
MathProf - Algebra - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Durchführung von Operationen
mit dem Taschenrechner für komplexe Zahlen.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Taschenrechner - Komplexer Taschenrechner - Real - Imaginär - Rechnen mit komplexen Zahlen - Realteil komplexer Zahlen - Imaginärteil komplexer Zahlen - Wurzel komplexer Zahlen - Komplexe Zahlen berechnen |
Taschenrechner für komplexe Zahlen
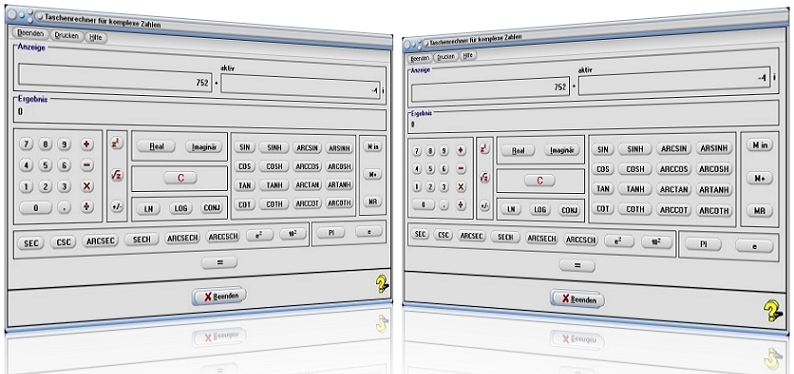
Modul Taschenrechner für komplexe Zahlen
Das kleine Unterprogramm [Algebra] - [Komplexe Zahlen] - Taschenrechner für komplexe Zahlen wurde implementiert, um einen Taschenrechner für komplexe Zahlen bereitzustellen.

In diesem Modul können numerische Berechnungen mit komplexen Zahlen mittels Mausbedienungen durchgeführt werden. Komplexe Zahlen können u.a. in arithmetischer, wie auch in trigonometrischer Form dargestellt werden:
Arithmetische Form: z = x + jy
Trigonometrische Form: z = r·(cos(φ) + j·sin(φ))
Die Definition dieser muss in diesem Modul in arithmetischer Form erfolgen.
Hinweis:
Im gesamten nachfolgend aufgeführten Text ist das Zeichen / als Symbolzeichen für Division zu interpretieren. Auf der Symbolschaltfläche im Unterprogramm wird ein synonymes Divisionssymbol hierfür verwendet.
Durch die Bedienung der Tasten Real und Imaginär legen Sie zunächst fest, für welchen Teil einer komplexen Zahl die Zahleneingaben zu übernehmen sind. Das Programm kennzeichnet den aktiven Bereich durch die Ausgabe des Texteintrags aktiv. Geben Sie hierauf durch die Bedienung der entsprechenden Zahlensymbol-Schaltflächen die Werte für den Real- bzw. den Imaginärteil der komplexen Zahl ein. Besitzt eine Zahl keinen Real- oder Imaginärteil, so belassen Sie diesen auf dem Vorgabewert 0.
Bei Bedarf leiten Sie hierauf durch die Verwendung der Symbolschaltflächen +, -, * oder / Operationen mit definierten Zahlen ein. Das Programm hat sich die zuerst definierte komplexe Zahl Z1 gemerkt. Im Eingabefeld erscheinen für den Real- wie auch den Imaginärteil die Werte 0. Nach einer erneuten Bedienung der Schaltflächen Realteil und Imaginärteil definieren Sie die Werte für die Zahl Z2 mit Hilfe der entsprechenden Zahlensymbol-Schaltflächen. Nach einem Klick auf den Schalter = gibt das Programm das Ergebnis, der mit den beiden komplexen Zahlen durchgeführten Operation, aus. Um eine mathematische Funktion zu benutzen (z.B. sin) definieren Sie zunächst die Werte für den Real- und den Imaginärteil der Zahl Z und bedienen erst hierauf die entsprechende Funktionssymbolschaltfläche.
Grundsätzlich gilt: Das Ergebnis einer Berechnung wird ausgegeben, nachdem die Taste = bedient wurde. Kann aufgrund mathematischer Fehler (z.B. Division durch 0) eine Rechenoperation nicht korrekt, oder nur unvollständig ausgeführt werden, so werden Sie durch das Erscheinen des Eintrages ERROR im Anzeigebereich darauf hingewiesen. Nach einer Bedienung der Taste C können Sie daraufhin in solch einem Fall wieder weiterarbeiten.
Mittels der Benutzung der Taste M in werden die Werte, der sich in den Anzeigefeldern ausgegebenen komplexen Zahl gespeichert. Soll eine bereits gespeicherte Zahl wieder geholt werden, so bedienen Sie die Taste MR. Die Taste M+ kann verwendet werden um einer berechneten Zahl den Wert, einer sich im Speicher befindenden Zahl, hinzu zu addieren.
Hinweis:
Nach der Durchführung einer Operation, bzw. einer Berechnung wird stets der Modus zur Eingabe des Realteils einer komplexen Zahl aktiviert.
Nachfolgend dargestellte Auflistung zeigt die Funktionen / Beschreibungen der zur Verfügung stehenden Bedienschalter:
| Schalter | Funktion / Beschreibung |
| 0...9 | Zifferntasten |
| +, -, *, / | Tasten für Operationen |
| , | Dezimaltrennzeichen |
| Real | Eingabemodus für Realteil der komplexen Zahl aktivieren |
| Imaginär | Eingabemodus für Imaginärteil der komplexen Zahl aktivieren |
| = | Durchführung einer Berechnung |
| C | Löschen der Berechnungsergebnisse |
| +/- | Vorzeichenwechsel |
| z² | Quadrierung einer komplexen Zahl |
| π | Kreiszahl Pi |
| e | Eulersche Zahl |
| ez,10z | Exponentialfunktionen ez und 10z |
| LN | Natürlicher Logarithmus |
| LOG | Dezimaler Logarithmus |
| SIN, COS, TAN, COT | Funktionen Sinus, Cosinus, Tangens, Cotangens |
| ARCSIN, ARCCOS, ARCTAN, ARCCOT | Funktionen Arcussinus, Arcuscosinus, Arcustangens, Arcuscotangens |
| SINH, COSH, TANH, COTH | Funktionen Sinus hyperbolicus, Cosinus hyperbolicus, Tangens hyperbolicus, Cotangens hyperbolicus |
| ARSINH, ARCOSH, ARTANH, ARCOTH | Funktionen Arcussinus hyperbolicus, Arcuscosinus hyperbolicus, Arcustangens hyperbolicus, Arcuscotangens hyperbolicus |
| SEC, CSC | Secans, Cosecans |
| ARCSECH, ARCCSCH | Arcussecans hyperbolicus, Arcuscosecans hyperbolicus |
| ARCSEC, ARCCSC | Arcussecans, Arcuscosecans |
| SECH, CSCH | Secans hyperbolicus, Cosecans hyperbolicus |
 | Wurzel einer komplexen Zahl |
| Min | Angezeigte Werte speichern |
| M+ | Angezeigte Werte zu Speicherinhalt addieren |
| MR | Speicherinhalt holen und ausgeben |
Eine Tastaturbedienung kann für folgende Bedienschalter angewandt werden:
Zifferntasten
Komma
Klammern
Taste C
Grundrechenoperationen
Taste = (Durchführung einer Berechnung)
Weitere Themenbereiche
Einheitskreis komplexer Zahlen
Schreibweisen komplexer Zahlen
Berechnungen mit komplexen Zahlen
Multiplikation komplexer Zahlen
Beispiele
Beispiel 1:
Um die beiden komplexen Zahlen
z1 = 4 - 2i
z2 = 6 + 8i
dividieren zu lassen, bedienen Sie nach einem Klick auf den Schalter C die weiteren zur Durchführung der Berechnung erforderlichen Schaltflächen wie folgt:
Real
4
Imaginär
2
± (zur Negierung der Zahl 2)
/
6
Imaginär
8
=
Als Ergebnis erhalten Sie nach einer Bedienung der Schaltfläche =:
z = z1 / z2 = 0,08 + 0,44i
Um eine neue Berechnung durchführen zu lassen, bedienen Sie zunächst den Schalter C.
Beispiel 2:
Es sind folgende Rechenoperationen auszuführen:
z = sin(3 - 4i)+1
Vorgehensweise:
Bedienen Sie nach einem Klick auf den Schalter C die weiteren zur Durchführung der Berechnung erforderlichen Schaltflächen nach folgendem Schema:
Real
3
Imaginär
4
± (zur Negierung der Zahl 4)
sin
+
Real
1
Als Ergebnis gibt das Programm nach einem Klick auf den Schalter = aus: z = 3.8537 + 27.016813i
Beispiel 3:
Es gilt, das Resultat der folgenden Berechnung ermitteln zu lassen:
z = 9i + 4·ln(3 + i)
Vorgehensweise:
Klicken Sie auf den Schalter C und bedienen Sie die erforderlichen Schaltflächen nach folgendem Schema:
Imaginär
9
+
4
*
ln
Real
3
Imaginär
1
Nach der Ausführung eines Klicks auf den Schalter = ermittelt das Programm: z = 1.70941 + 11.648635i
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle

Beispiel 1

Beispiel 2
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.
Wikipedia - Komplexe Zahl
Wikipedia - Imaginäre Zahl
Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Zahlen I - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte
MathProf 5.0 - Unterprogramm Schreibweisen komplexer Zahlen

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















