MathProf - Sekante - Steigung - Änderungsrate - Sekantengleichung

     

Modul Tangente - Sekante

---

MathProf ermöglicht neben der Anwendung als Berechnungs- und Visualisierungsprogramm die Durchführung von Untersuchungen zu Grundlagen sowie die Aneignung fundamentierten Fachwissens zu vielen Themengebieten der Analysis.

Das Modul [Analysis] - [Tangente - Normale - Sekante] - Tangente - Sekante stellt eine Ergänzung zum Unterprogramm Kurvendiskussion dar, und ermöglicht die Analyse der Herleitung der Differentialrechnung anhand des 'Sekantenproblems' mittels dem grafischen Differenzieren von Funktionen.

 

 
Der Differentialquotient an einer Stelle x₀ lässt sich durch eine Grenzwertbildung des Differenzenquotienten erhalten. Die Steigung (der Anstieg) m_s einer Sekante (Sekantensteigung) ist der Grenzwert einer Tangentensteigung m_t. Sind zwei Punkte P(x₀;y₀) und Q(x₀+Δx,f(x₀+Δx)) die auf der Funktionskurve f(x) liegen gegeben, so errechnet sich die Sekantensteigung aus dem Differentialquotienten
 

 

Wandert der Punkt Q auf der Kurve auf den Punkt P zu, so besitzt die Tangente in Punkt P den Steigungswert
 

 

Dieser Grenzwert wird als 1. Ableitung f'(x) der Funktion f(x) an der Stelle x₀, oder als Differentialquotient bezeichnet. Der Differenzenquotient zwischen den beiden Stellen x_0​ und x_0​+Δx ​erteilt Auskunft über die Steigung, die die Sekante zwischen den Punkten P und Q besitzt. Er berechnet die mittlere Änderungsrate.
 
In diesem Programmteil wird diese Stelle x₀ mit Px bzw. Qx bezeichnet. Die Ermittelbarkeit einer Sekante bzw. Tangente hängt von der Differenzierbarkeit der zu untersuchenden Funktion ab.

Die Tangentensteigung beschreibt im Gegensatz zur Sekantensteigung, die Steigung einer Tangente, die eine Kurve in genau einem Punkt berührt.

Als Sekantengleichung oder Sekantensteigungsfunktion wird die Gleichung bzw. Funktion bezeichnet, die die Steigung einer Sekante beschreibt. Sie besitzt die Gestalt einer linearen Funktion der Form f(x) = mx + b.

Als Tangentenproblem wird die Aufgabe bezeichnet, bei der untersucht wird, ob in einem bestimmten Punkt einer Kurve eine Tangente existiert. Hierbei ist deren Steigung zu ermitteln und es wird sowohl der Differenzenquotient wie auch der Differentialquotient berechnet.
  

 
Mittelwertsatz der Differenzialrechnung (mittlere Änderungsrate):

Ist f:[a,b]→ℝ eine stetige Funktion, welche im Bereich (a,b) differenzierbar ist, so gibt es eine Stelle x0 ∈ (a,b), für welche gilt:



Dieser Wert wird als mittlere Änderungsrate, durchschnittliche Änderungsrate oder durchschnittliche Steigung bezeichnet.
    
Lokale Änderungsrate:

Die lokale Änderungsrate einer Funktion beschreibt deren Steigung in einem bestimmten Punkt. Sie ist wie folgt definiert:



Lokale Änderungsrate unter Anwendung der h-Methode:

Die lokale Änderungsrate einer Funktion kann auch mit Hilfe der sogenannten h-Methode bestimmt werden. Sie ist eine alternative Interpretation der lokalen Änderungsrate. Ihre Definition lautet:



Anstelle des Werts für x → x₀ läuft in diesem Fall die Differenz h = x-x₀ gegen den Wert 0.

Positive Steigung - Negative Steigung:

Steigt eine Funktion in positiver x-Richtung an, so ist ihre Steigung positiv (m > 0). Im umgekehrten Fall ist sie negativ (m < 0).
 
Änderungsmaße:

Absolute Änderung von f in [a;b]:  f(b) - f(a) 
Relative Änderung von f in [a;b]:  (f(b) - f(a))/ f(a)
Prozentuale Änderung von f in [a;b]:  (f(b) - f(a))/ f(a)·100
Mittlere Änderung von f in [a;b]:  (f(b) - f(a))/(b-a)
Änderungsfaktor von f in [a;b]:  f(a)/f(b)

---

Kurzbeschreibung oben aufgeführter Begriffe hinsichtlich Änderungsmaßen:

1. Als relative Änderung wird die absolute Änderung bezeichnet, die diese gegenüber dem Grudwert besitzt. Sie wird gebildet, indem der erste Wert von einem zweiten Wert subtrahiert wird und diese Differenz hierauf durch den Absolutwert des Ausgangswerts dividiert wird. Es gilt:

Relative Änderung = (Neuer Wert -  Anfangswert / Anfangswert

2. Als absolute Änderung wird die Differenz zweier Zahlen bezeichnet. Sie wird berechnet, indem der entsprechende Anfangswert von einem zweiten Wert subtrahiert wird. Es gilt:

Absolute Änderung = Neuer Wert − Anfangswert

3. Als prozentuale Änderung wird das Verhältnis zwischen einem alten Wert und einem neuen Wert bezeichnet. Es gilt:

Prozentuale Änderung = (Endwert -  Anfangswert) / Anfangswert · 100

4. Als mittlere Änderungsrate wird die durchschnittliche Steigung m bezeichnet, die zwischen zwei Punkten a und b (einem Intervall) des Graphen einer Funktion vorhanden ist.

Die mittlere Änderungsrate beträgt: m = (f(b) - f(a))/ (b-a)

5. Als Änderungsfaktor wird die Zahl bezeichnet, mit welcher ein ursprünglicher Wert multipliziert wird um die entsprechende Menge nach der durchgeführten Änderung zu erhalten. Der Änderungsfaktor ist stets um den Wert 1 größer als die relative Änderung.

Die momentane Änderungsrate (Ableitung) entspricht der Steigung der Tangente in einem entsprechenden Punkt.

Alle zuvor aufgeführten Änderungen besitzen keine physikalische Einheiten.

   

 
Linearisierung einer Funktion:

Eine in Punkt P(x₀,y₀) differenzierbare Funktion y = f(x) besitzt dort eine eindeutig bestimmte Tangente. In diesem meist als Arbeitspunkt bezeichneten Ort wird die dortige Kurventangente durch eine lineare Funktion ersetzt. Sie wird als linearisierte Funktion bezeichnet. Ihre Gleichung lautet:

y - y₀ = f'(x₀ - x)·(x - x₀)

bzw.

Δy = f'(x₀)·Δx

Δx und Δy sind die sogenannten Relativkoordinaten bzgl. des Arbeitspunkts P.
 

 

 
Dieses Modul ermöglicht es, Untersuchungen zum Thema Tangente - Sekante durchzuführen. Hierbei werden u.a. die Ergebnisse folgender Berechnungen ausgegeben:
 

• Funktionswerte an den Stellen Px und Qx
• Steigung der durch die Punkte P und Q verlaufenden Sekante (Sekantensteigung bzw. Änderungsrate)
• Steigungswinkel der durch die Punkte P und Q verlaufenden Sekante (Sekantenwinkel)
• Gleichung der durch die Punkte P und Q verlaufenden Sekante (Sekantengleichung)
• Abstand der durch die Punkte P und Q verlaufenden Sekante zum Koordinatenursprung
• Nullstelle der durch die Punkte P und Q verlaufenden Sekante

 
Bei Ausgabe der grafischen Darstellung werden zudem ermittelt:
 

• Steigung der durch Punkt P verlaufenden Tangente (Tangentensteigung)
• Steigungswinkel der durch Punkt P verlaufenden Tangente (Tangentenwinkel)
• Gleichung der durch Punkt P verlaufenden Tangente (Tangentengleichung)

 
Es werden zwei verschiedene Möglichkeiten angeboten, Untersuchungen grafisch durchzuführen.
 

 
Um Sekanten bzw. Tangenten an eine oder zwei verschiedene Stellen einer explizit definierten Funktion legen und untersuchen zu lassen, sollten Sie Folgendes ausführen:
 

1. Definieren Sie den entsprechenden Funktionsterm im dafür vorgesehenen Eingabefeld mit der Bezeichnung f(x) =. Beachten Sie hierbei die geltenden Syntaxregeln.
    

2. Legen Sie die Abszissenwerte der zu untersuchenden Stellen Px sowie Qx in den dafür zur Verfügung stehenden Eingabefeldern fest.
    

3. Nach einer Bedienung der Schaltfläche Berechnen werden die ermittelten Ergebnisse in der Tabelle ausgegeben.
    

4. Um den Sekantenverlauf bei bestimmten Stellen einer Funktion grafisch zu analysieren, sollten Sie folgendermaßen verfahren:
   
   Aktivieren Sie das Kontrollkästchen Zu untersuchende Stellen (Px bzw. Qx) verwenden und bedienen Sie die Schaltfläche Darstellen.
   
   Beim Aufruf der Darstellung benutzt das Programm in diesem Fall stets die beiden in den Eingabefeldern festgelegten Abszissenwerte für Px und Qx. Möchten Sie die Position (Abszissenwerte) von Punkt P oder Punkt Q verändern, so bedienen Sie die Schaltfläche Punkte auf dem Bedienformular und geben die entsprechenden Zahlenwerte im daraufhin erscheinenden Formular ein. Übernommen werden diese, wenn Sie auf die sich dort befindende Schaltfläche Ok klicken.
    
5. Um eine prinzipielle grafische Analyse des Sekantenproblems durchführen zu lassen, gehen Sie wie nachfolgend beschrieben vor:
   
   Deaktivieren Sie das Kontrollkästchen Zu untersuchende Stellen (Px bzw. Qx) verwenden und bedienen Sie die Schaltfläche Darstellen.
   
   Beim Aufruf der Darstellung benutzt das Programm in diesem Fall stets die Startwerte Px = 0 und Qx = 2 (die in Eingabefeldern definierten Koordinatenwerte werden ignoriert). Möchten Sie die Abszissenwerte der Punkte P oder Q innerhalb des vorgegebenen Wertebereichs -10 ≤ x ≤ 10 verändern, so positionieren Sie die zur Verfügung stehenden Rollbalken.
   
   Um Zusammenhänge mit Hilfe von Simulationen zu analysieren und Punkt P horizontal zu bewegen, bedienen Sie die Schaltfläche Simulation. Hierauf können Sie ggf. den Wert für die zu verwendende Schrittweite einstellen. Ändern Sie diesen bei Bedarf und bestätigen Sie mit OK. Beendet werden kann die Ausführung einer derartigen Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.
    
6. Durch die Aktivierung des Kontrollkästchens Tangente können Sie die Einblendung der durch Punkt P an der Stelle Px verlaufenden Kurventangente veranlassen. Eine Aktivierung des Kontrollkästchens 1. Ableitung bewirkt die Darstellung der 1. Ableitung der zu untersuchenden Funktion. Das ermittelte Sekantendreieck kann durch die Benutzung des Kontrollkästchens Sekantendreieck ein- bzw. ausgeblendet werden. Eine Darstellung von Hilfslinien kann durch die Aktivierung des Kontrollkästchens Hilfslinien bewirkt werden.

 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.

  

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

Wurde auf dem Hauptformular des Unterprogramms das Kontrollkästchen Zu untersuchende Stellen (Px bzw. Qx) verwenden aktiviert (voreingestellt), so wird nachfolgend gezeigtes Bedienformular zur Verfügung gestellt.

 

 

Wurde auf dem Hauptformular dieses Moduls das o.a. Kontrollkästchen deaktiviert, so blendet das Programm nachfolgend gezeigtes Bedienformular ein.

 

 

Analytische Ermittlung von Ableitungen

 
Unter dem Menüpunkt Ableitung analytisch können Sie sich die 1. Ableitung der definierten Funktion f(x) symbolisch differenziert ausgeben lassen. Es erscheint ein Formular.
 

1. Definieren Sie die Funktion, gemäß den geltenden Syntaxregeln, im Eingabefeld mit der Bezeichnung Y = f(x) =.
    
2. Nach der korrekten Deklaration der Funktion im Eingabefeld und der Bedienung des Schalters Ermitteln wird die 1. Ableitung der eingegebenen Funktion ermittelt und in den entsprechenden Ausgabefeldern angezeigt.

 
Ist die Funktionsdeklaration zu komplex um eine Ableitung symbolisch differenzieren zu können, so erscheint der Eintrag 'Funktion zu komplex - nicht differenzierbar' in den Ausgabefeldern.

Durch die Bedienung der dortigen Schaltfläche Schließen, kehren Sie wieder zum Unterprogramm zurück.

Hinweis:

Beinhaltet eine Funktionsdeklaration den Parameter P, so erhalten Sie eine Fehlermeldung, da parameterhaltige Funktionen nicht analytisch differenziert werden können.

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Mathematische Funktionen II

Tangente – Normale

Tangente und Normale von externem Punkt

Kurvendiskussion

 

 

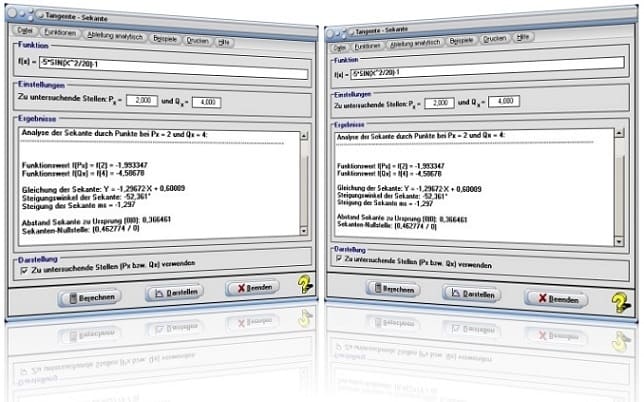
Es gilt, Untersuchungen mit der Funktion f(x) = (x+5)²/10-4 an den Stellen Px = 1 und Qx = 2 bzgl. der Ermittlung von Sekanten durchführen zu lassen.

 

Vorgehensweise und Lösung:

 

Nach einer Eingabe des Terms (X+5)^2/10-4 in das Feld f(x) = sowie der Festlegung der Koordinatenwerte für die zu untersuchenden Stellen in den entsprechenden Feldern und einer Bedienung des Schalters Berechnen erhalten Sie folgende Ergebnisse:

 

Funktionswert f(Px) = f(1) = -0,4  
(Y-Koordinatenwert der Funktion an Stelle Px = 1)

Funktionswert f(Qx) = f(2) = 0,9

(Y-Koordinatenwert der Funktion an Stelle Qx = 2)

Gleichung der Sekante (Sekantengleichung): Y = 1,3·X - 1,7
Steigungswinkel der Sekante: 52,431°
Steigung der Sekante: ms = 1,3

Abstand der Sekante zum Koordinatenursprung (0|0): 1,036508
Nullstelle der Sekante: (1,307692 / 0)
 

Deaktivieren Sie das Kontrollkästchen Zu untersuchende Stellen (Px bzw. Qx) verwenden, lassen Sie sich die Funktion nach einem Klick auf die Schaltfläche Darstellen grafisch ausgeben und verändern Sie den Abszissenwert des Punktes P unter der Bedienung des Rollbalkens X-Pos. Punkt P so (ohne Veränderung der Ursprungsposition von Punkt Q), dass dieser sich in Richtung des Punktes Q bewegt.

 

Hierbei kann festgestellt werden, dass die Sekante bei P_x = 2 in eine Tangente übergeht und die 1. Ableitung der Funktion an Stelle x = 2 den Wert y' = 1,4 besitzt, da die (Sekantensteigung) Tangentensteigung in diesem Punkt m_t = 1,4 beträgt.
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3


Grafische Darstellung - Beispiel 4


Grafische Darstellung - Beispiel 5


Grafische Darstellung - Beispiel 6
   

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Tangente und unter Wikipedia - Sekante zu finden.

 

 
 

Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Segmentweise definierte Funktionen - Kurvenscharen - Funktionsparameteranalyse - Funktionswertetabellen - Iteration - Parameter der Sinus- und Cosinusfunktion - Parameter der Logarithmusfunktion - Parameter der Betragsfunktion - Parameter der Integer-Funktion - Parameter der Quadratwurzelfunktion - Parameter der Potenzfunktion - Parameter der Exponentialfunktion - Kubische Funktion in allgemeiner Form - Kubische Funktion in spezieller Form - Zahlenfolgen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Rekursive Zahlenfolgen - Interaktiv - Arithmetische und geometrische Zahlenfolgen - Parabelgleichungen - Parabelgleichungen - Interaktiv - Parabel und Gerade - Interaktiv - Analyse quadratischer Funktionen - Ermittlung ganzrationaler Funktionen - Ganzrationale Funktionen (Polynome) - Ganzrationale Funktionen (Polynome) - Interaktiv - Gebrochenrationale Funktionen - Gebrochenrationale Funktionen - Interaktiv - Interpolation nach Newton und Lagrange - Interpolation ganzrationaler Funktionen - Polynomregression - Nullstellen - Iterationsverfahren - Horner-Schema - Tangente - Normale - Tangente und Normale von externem Punkt - Kurvendiskussion - Kurvendiskussion - Interaktiv - Obersummen und Untersummen - Obersummen und Untersummen - Interaktiv - Integrationsmethoden - Rotationsparaboloid (3D) - Integralrechnung - Integralrechnung - Interaktiv - Zykloide - Hypozykloide - Epizykloide - Sternkurven - Zissoide - Strophoide - Kartesisches Blatt - Semikubische Parabel - Archimedische Spirale - Logarithmische Spirale - Fourier-Summen - Fourier-Reihen - Taylorreihen und Potenzreihen - Implizite Funktionen
 

 

Startfenster des Unterprogramms Tangente - Sekante
 

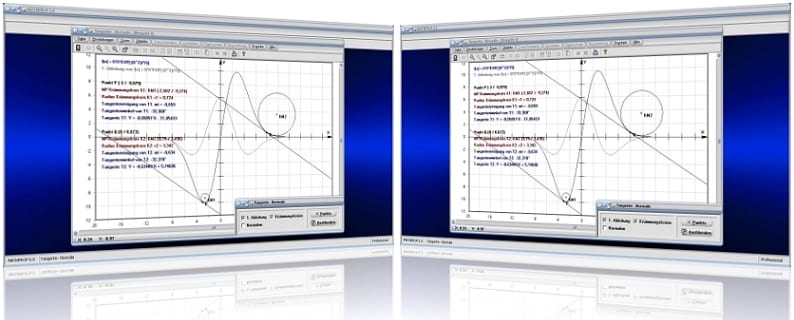
MathProf 5.0 - Unterprogramm Tangente - Normale

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---