Startseite » MathProf - F-Verteilung - Gammaverteilung - Logistische Verteilung

MathProf - F-Verteilung - Gammaverteilung - Logistische Verteilung

MathProf - Mathematik-Software - Stetige Verteilung | Normalverteilung | Grafik | Statistik

Fachthemen:
Verteilungen - Beta-Verteilung - Cauchy-Verteilung - Chi ²-Verteilung - Exponentialverteilung - F-Verteilung - Gamma-Verteilung - Laplace-Verteilung - Logistische Verteilung - Logarithmische Normalverteilung - Gaußsche Normalverteilung - Standard-Normalverteilung - Pareto-Verteilung - Student-t-Verteilung - Dreiecksverteilung - Uniform-Verteilung - Gleichverteilung (Rechteckverteilung) - Weibull-Verteilung - Negative Binomialverteilung - Maxwell-Verteilungen

MathProf - Stochastik - Statistik - Software für interaktive und numerische Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

MathProf - Mathematik für Schule, Studium und Wissenschaft - Stetige Verteilung | Normalverteilung | Grafik | Statistik

Online-Hilfe
für das Modul zur Durchführung von Analysen mit stetig verteilten Zufallsgrößen sowie zur Ausgabe der Werte für Dichte und Verteilung einer Wahrscheinlichkeit in Tabellen und Diagrammen.

Der in diesem Teilprogramm implementierte Rechner ermöglicht die Durchführung der Wahrscheinlichkeitsrechung mit häufig verwendeten stetigen Verteilungen sowie die grafische Darstellung derer Wahrscheinlichkeitsfunktion (Verteilungsfunktion) und Dichtefunktion (Wahrscheinlichkeitsdichte).

Die vom Programm numerisch ermittelten Lösungen werden in einer Tabelle ausgegeben und lassen sich ausdrucken.

Nach einer Festlegung der Werte der entsprechenden Parameter erfolgt das Berechnen der Quantile (Perzentile) der gewählten stetigen Wahrscheinlichkeitsverteilung.

Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Moduls im Programm geben und dazu dienlich sind, Aufgaben zu diesem Themengebiet zu lösen, sind eingebunden.

MathProf - Software für interaktive Mathematik

Weitere relevante Seiten zu diesem Programm

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Videoauswahl zu MathProf 5.0.

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche können Sie eine kostenlose Demoversion des Programms MathProf 5.0 herunterladen.

Zum Download der Demoversion von MathProf 5.0

Themen und Stichworte zu diesem Modul:

Stetige Verteilungen - Betaverteilung - Beta Verteilung - Cauchy-Verteilung - Chi-Quadrat-Verteilung - Exponentialverteilung - F-Verteilung - Gammaverteilung - Laplace-Verteilung - Logistische Verteilung - Logarithmische Normalverteilung - Logarithmische Verteilung - Lognormalverteilung - Normalverteilung - Fisher-Verteilung - Normalverteilte Zufallsvariable - Gaußsche Normalverteilung - Standardnormalverteilung - Pareto-Verteilung - Student-t-Verteilung - t-Verteilung - Dreiecksverteilung - Uniform-Verteilung - Weibull-Verteilung - Maxwell-Verteilung - Negative Binomialverteilung - Studentsche t-Verteilung - Gleichverteilung - Rechteckverteilung - Diskrete Gleichverteilung - Stetige Verteilungen - Verteilungen - Verteilung - Quantilfunktion - Stetige Verteilungsfunktionen - Stetige Verteilung - Wahrscheinlichkeitsfunktion - Stetige Variablen - Wert - Funktion - Häufigkeit - Varianz - Intervall - Berechnen - Bestimmen - Einführung - Plotten - Grafik - Graph - Grafisch - Plot - Plotter - Beispiel - Erklärung - Beschreibung - Definition - Verteilungsfunktion - Verteilungstabelle - Dichtefunktion - Erwartungswert - Rechner - Präsentation - Übersicht - Tabelle - Bild - Darstellung - Eigenschaften - Zufallsvariablen - Berechnung - Darstellen - Zeichnen - Stetige Zufallsgröße - Stetige Zufallsvariable - Stetige Gleichverteilung - Wahrscheinlichkeitsrechnung - Quantile - Z-Wert - F-Wert - T-Wert - Φ(z)-Tabelle - Koeffizient - Koeffizienten - t-Verteilungstabelle - Normalverteilungstabelle - Signifikanzniveau - Lambda - Integral - Exponentialverteilt - Normalverteilt - Daten - Inverse Normalverteilung - Dichtetabelle - Verteilungsdichte - Verteilungsdiagramm - Freiheitsgrade - Auswertung - Auswerten - Zusammenhänge - Dichte - Diagramme - Normalverteilungskurve - PDF - CDF - NormCDF - NormalCDF - NormalPDF - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Bedeutung - Was bedeutet - Was ist - Wieviel - Sigma - Phi-Tabelle - Sigma-Tabelle - Perzentile - 0,9 - 0,95 - 0,975 - 0,99 - 0,995 - 0,1 - 0,05 - 0,025 - 0,01 - 0,005 - p Wert - p Werte - Quantil - Wahrscheinlichkeit - Symmetrisches Intervall - Symmetrisch - Asymmetrisch - Kumulative Verteilungsfunktion - Kumulierte Normalverteilung - Kumulierte Häufigkeit - Kumulierte Standardnormalverteilung - Kumulierte Wahrscheinlichkeit - Kumulierte relative Häufigkeit - Kumuliert - Kumulierte Verteilungsfunktion - Formel - Parameter - Varianz - Wahrscheinlichkeitsdichtefunktion - Wahrscheinlichkeitsverteilung - Inverse - Inverse Verteilungsfunktion - Gleichverteilt

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zum Inhaltsverzeichnis der in MathProf 5.0 implementierten Module bzw. zur Bestellseite für das Programm.

Stetige Verteilungen

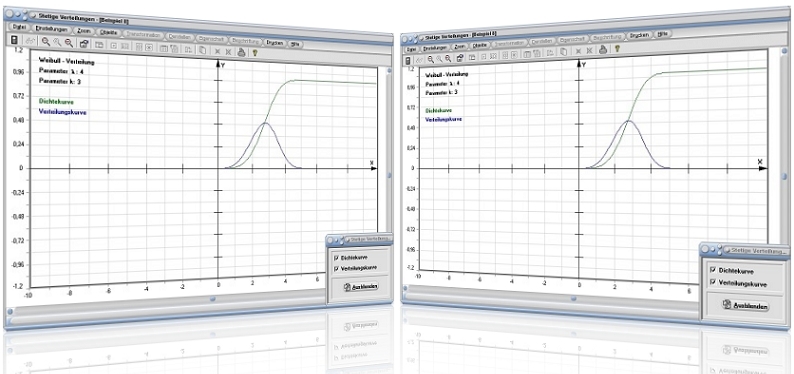
Modul Stetige Verteilungen

Im Unterprogramm [Stochastik] - [Stetige Verteilungen] - Stetige Verteilungen lassen sich statistische Berechnungen mit stetigen Verteilungen durchführen. Ermittelte Werte (Dichte, Verteilung und Quantile) werden in Tabellen ausgegeben und Zusammenhänge zu diesem Fachthema können grafisch veranschaulicht werden.

MathProf - Stetige Verteilung - Dichte - Chi-Quadrat-Verteilung - Tabelle - Normalverteilung - Wahrscheinlichkeitsfunktion - Wahrscheinlichkeitsverteilung - Quantile - Freiheitsgrad - Dichtefunktion - Verteilungfunktion - Stetige Verteilungen - Rechner - Berechnen - Präsentation - Übersicht - Bild - Eigenschaften - Zufallsvariablen - Berechnung

Abbildung 1 - Dichte und Verteilung

MathProf - F-Verteilung - Perzentile - Dichte - Tabelle - Gammaverteilung - Inverse Normalverteilung - Diagramme - Quantil - Kumulierte relative Häufigkeit - Normalverteilung - Quantile - Freiheitsgrad - Dichtefunktion - Verteilungfunktion - Stetige Verteilungen - Rechner - Berechnen - Häufigkeit - Varianz - Intervall - Bestimmen - Erklärung - Beschreibung - Definition - Verteilungstabelle - Erwartungswert

Abbildung 2 - Quantile

Stetige Verteilungen (stetige Verteilungsfunktionen) beschreiben Wahrscheinlichkeitsverteilungen, bei welchen die Zufallsgröße innerhalb eines Bereichs reelle Zahlenwerte annehmen kann. Bei diskreten Verteilungen hingegen sind dies nur ganzzahlige Werte. Eine Zufallsvariable heißt stetig, wenn sie in jedem beschränkten Intervall a ≤ x ≤ b unendlich viele Ausprägungen besitzen kann. Eine stetige Zufallsvariable kann unabhängig von der Messgenauigkeit sämtliche (unendlich viele) Werte einer kontinuierlichen Menge annehmen. Sie bildet sich meist durch Messvorgänge. Beispielsweise sind für die Körpergröße eines Menschen theoretisch unendlich viele Werte zwischen 168,4 cm und 172,3 cm möglich. Derartige Wertebereiche werden als überabzählbar unendlich bezeichnet.

Mit Hilfe dieses Moduls können Werte für die Dichte und Verteilung folgender stetiger Verteilungsfunktionen errechnet werden:

Beta-Verteilung (Betaverteilung)
Cauchy-Verteilung
Chi ²-Verteilung (Chi-Quadrat-Verteilung mit Freiheitsgrad)
Exponentialverteilung
F-Verteilung (Fisher-Verteilung mit Freiheitsgrad)
Gamma-Verteilung
Laplace-Verteilung
Logistische Verteilung
Logarithmische Normalverteilung
Gaußsche Normalverteilung
Standard-Normalverteilung (Normierte Normalverteilung)
Pareto-Verteilung
Student-t-Verteilung (mit Freiheitsgrad)
Dreiecksverteilung (Triangularverteilung)
Uniform-Verteilung (Gleichverteilung)
Weibull-Verteilung
Negative Binomialverteilung
Maxwell-Verteilung

Darüber hinaus ist es möglich, die Quantile für Irrtumswahrscheinlichkeiten der entsprechenden Verteilungsarten ermitteln zu lassen.

Berechnung und Darstellung

MathProf - Wahrscheinlichkeitsfunktion - Stetige Zufallsgröße - Stetige Zufallsvariable - Stetige Gleichverteilung - Z - Wert - Wert - T - Wert - F(z) - Koeffizient - Koeffizienten - Verteilungstabelle - Normalverteilungstabelle - Signifikanzniveau - Lambda - Integral - Daten - Dichtetabelle - Dichtefunktion - Wahrscheinlichkeitsrechnung - Laplace-Verteilung - Freiheitsgrade - Verteilungsfunktion - Wahrscheinlichkeitsverteilung - Stetige Verteilungen - Rechner - Berechnen

Um Wahrscheinlichkeitsberechnungen mit stetig verteilten Größen durchführen zu lassen und sich Zusammenhänge grafisch zu veranschaulichen, sollten Sie folgendermaßen vorgehen:

Wählen Sie durch einen Klick auf das entsprechende Registerblatt Dichte und Verteilung aus, ob Dichte oder Verteilung einer Verteilungsart ermittelt werden sollen.
Selektieren Sie durch die zur Verfügung stehende Auswahlbox Verteilungsart, mit welcher Verteilungsart Berechnungen durchzuführen sind.
Legen Sie die benötigten Parameterwerte bzw. Freiheitsgrade durch die Eingabe der entsprechenden Zahlen in die dafür vorgesehenen Felder im Formularbereich Parameter fest.

Bei den Verteilungsarten sind die Werte folgender Parameter bzw. Freiheitsgrade festzulegen:

Beta-Verteilung: Parameter α und β
Cauchy-Verteilung: Parameter x₀ und γ
Chi²-Verteilung: Freiheitsgrad F
Exponential-Verteilung: Parameter λ
F-Verteilung: Freiheitsgrad F1 und Freiheitsgrad F2
Gamma-Verteilung: Parameter k und φ
Laplace-Verteilung: Parameter μ und b
Logistische Verteilung: Parameter μ und s
Logarithmische Normalverteilung: Parameter μ und s²
Gauß'sche Normalverteilung: Parameter μ und σ²
Standard-Normalverteilung: -----
Pareto-Verteilung: Parameter k und x_m
Student-t-Verteilung: Freiheitsgrad F
Dreiecksverteilung: Parameter a, b und c
Uniform-Verteilung: Parameter a und b
Weibull-Verteilung: Parameter λ und k
Neg. Binomialverteilung: Parameter k und r
Maxwell-Verteilung: Parameter a
Definieren Sie den Wertebereich (von x1...bis x2) und die zur Berechnung erforderliche Schrittweite durch die Eingabe der entsprechenden Werte in die dafür vorgesehenen Felder.
Bedienen Sie die Schaltfläche Berechnen, so werden die Ergebnisse in den zur Verfügung stehenden Tabellen ausgegeben.
Dichte- und Verteilungsskurven können Sie sich anzeigen lassen, indem Sie die Schaltfläche Darstellen bedienen.

Möchten Sie die Ergebnisse der zuletzt durchgeführten Berechnung löschen, so bedienen Sie hierfür die Schaltfläche Löschen.

Fachbegriffe

Kumulative Verteilungsfunktion: Eine kumulative Verteilungsfunktion beschreibt die Wahrscheinlichkeit mit der alle Werte bis hin zu einer bestimmten Grenze eintreten können.

Kumulierte Häufigkeit (Summenhäufigkeit oder kumulierte relative Häufigkeit): Die kumulierte Häufigkeit (Summenhäufigkeit oder kumulierte relative Häufigkeit) ist ein Maß der deskriptiven Statistik, welches die Häufigkeit angibt, mit der ein Merkmal kleiner gleich einer bestimmten Schranke ist.

Quantilfunktion: Als Quantilfunktion wird die inverse Funktion einer Verteilungsfunktion bezeichnet. Sie beschreibt den zu einer bestimmten Wahrscheinlichkeit zugeordneten Wert einer Variable.

Eine Wahrscheinlichkeitsfunktion (Zähldichte) ist eine spezielle Funktion in der Stochastik ist eine Beziehung zwischen zwei Mengen, die jedem Element einer dieser Mengen exakt ein Element der anderen Menge zuordnet.

Freiheitsgrad: Freiheitsgrade geben die Anzahl frei bestimmbarer Werte für den Parameter einer Verteilung an. Die Zahl der Freiheitsgrade erhöht sich bei zunehmender Stichprobengröße und reduziert sich mit der Anzahl angenommener Parameter.

Dichtefunktion (Wahrscheinlichkeitsdichtefunktion): Eine Dichtefunktion beschreibt bei einer diskreten Verteilung, mit welcher Wahrscheinlichkeit eine Zufallsvariable eine bestimmte Merkmalsausprägung annimmt. Eine Dichtefunktion wird auch als Wahrscheinlichkeitsdichte, Verteilungsdichte oder Dichte bezeichnet. Sie wird bei stetigen Verteilungen als Wahrscheinlichkeitsdichtefunktion bezeichnet. Beim Vorliegen einer diskreten Verteilung ist die Anzahl der Zufallsvariablen endlich und ihre Werte sind exakt definiert.

Inverse Funktion - Quantil-Funktion - Inverse Verteilungsfunktion: Allen Verteilungsfunktionen können inverse Verteilungsfunktionen zugeordnet werden, die unter gewissen Voraussetzungen die inversen Funktionen der Verteilungsfunktionen sind. Eine inverse Verteilungsfunktion (Quantil-Funktion) ordnet jeder Zahl zwischen null und eins den kleinsten Wert zu, an welchem die Verteilungsfunktion diese Zahl übersteigt.

Inverse Normalverteilung: Bei der inversen Normalverteilung handelt es sich um eine kontinuierliche Wahrscheinlichkeitsverteilung die bei verallgemeinerten linearen Modellen Anwendung findet.

Normalverteilte Zufallsvariable: Als normalverteilte Zufallsvariable mit den Parametern und wird eine stetige Zufallsvariable bezeichnet, die durch ihre Standardabweichung σ sowie ihren Erwartungswert μ definiert ist und nach Durchführung einer Standardisierung der Form z = (k - μ) / σ als Dichtefunktion die Gaußsche Glockenkurve besitzt.

Erwartungswert: Der Erwartungswert einer Zufallsvariablen erteilt Auskunft darüber, welcher durchschnittliche Wert (Mittelwert) bei einer großen Häufigkeit von Durchführungen eines Zufallsexperiment für die Zufallsvariable zu erwarten ist.

Zufallsvariable (Zufallsgröße): Als Zufallsvariablen oder Zufallsgrößen werden in der Stochastik Zuordnungsvorschriften bezeichnet, die jedem möglichen Ergebnis eines durchgeführten Zufallsexperiments eine Größe zuordnet.

Stetige Zufallsgröße: Eine Zufallsgröße wird als stetig bezeichnet, wenn sie keine Lücken aufweist und somit alle sich innerhalb eines Werte Intervalls befindenden Werte annehmen kann.

Stetige Zufallsvariable (stetige Variable): Als stetige Zufallsvariable oder stetige Variable wird eine Variable bezeichnet, deren annehmbare Werte nicht abzählbar sind. Variablen dieser Art kommen häufig bei der Analyse von Messwerten wie Temperatur, Gewicht oder der Zeit vor.

Arbeitsblätter - Unterrichtsmaterialien - Nutzung zu Unterrichtszwecken

Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.

Aufgaben - Lernen - Üben - Übungen

Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Grafikprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Üben sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Benutzbarbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Übungen hierzu. Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens genutzt werden.

Oftmals lassen sich hiermit auch die Lösungen von Übungsaufgaben durch benutzerdefinierte Festlegungen und Eingaben numerisch oder grafisch ermitteln bzw. auswerten. Erlernte Fertigkeiten können somit auf anschauliche Weise untersucht werden. Implementierte Beispiele zu Sachverhalten erlauben die Bezugnahme zum entsprechenden Fachthemengebiet.

Mittels der anschaulichen Gestaltung und leichten Bedienbarbarkeit der einzelnen Module dieser Software werden oftmals häufig gestellte Fragen mit den Anfangsworten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? zum entsprechenden Themengebiet auf verständliche Weise beantwortet und einfach erklärt sich durch dessen Benutzung vieles von alleine. Zudem liefert diese Applikation zu vielen gestellten Fragen eine verständliche Antwort, Beschreibung und Erklärung.

Video

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in MathProf implementierten Modulen sind auf Youtube unter den folgenden Adressen abrufbar:

Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle

Bedienformular

MathProf - Maxwell-Verteilung - Wahrscheinlichkeitsrechnung - Wahrscheinlichkeitsdichte - Quantile - Freiheitsgrad

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:

Dichtekurve: Darstellung der Dichtekurve der Verteilung ein-/ausschalten
Verteilungskurve: Darstellung der Verteilungskurve der Verteilung ein-/ausschalten

Allgemein

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

Kurzbeschreibungen - Übersicht

Kurzbeschreibungen zu den in diesem Modul zur Verfügung stehenden Verteilungsarten:

Eine Chi-Quadrat-Verteilung ist eine stetige Verteilung, welche k Freiheitsgrade besitzt. Sie wird verwendet, um die Verteilung einer Summe von quadrierten Zufallsvariablen zu beschreiben. Auch wird sie eingesetzt, um die Anpassungsfähigkeit einer Datenverteilung zu testen und um festzustellen, ob Datenreihen unabhängig sind. Zudem findet Sie Anwendung um die Konfidenzwerte für die Varianz und Standardabweichung einer Zufallsvariable aus einer Normalverteilung zu schätzen. Sie ist ein Sonderfall der Gamma-Verteilung.

Die Beta-Verteilung findet Anwendung um kontinuierliche Zufallsvariablen zu beschreiben, deren Bereich zwischen 0 und 1 liegt. Sie wird zur Modellierung der Unsicherheit hinsichtlich der Erfolgswahrscheinlichkeit eines Experiments verwendet.

Die Cauchy-Verteilung ist ein spezieller Fall der stabilen Wahrscheinlichkeitsverteilungen. Sie ist identisch mit der Student-t-Verteilung mit einem Freiheitsgrad. Bei der Risikoanalyse findet sie wenig Anwendung. Vielmehr kommt sie Kalibrierungsproblemen zum Einsatz. Ihre Verteilung ist symmetrisch um den Parameter x₀. Die Streuung der Verteilung nimmt mit zunehmendem γ zu.

Bei der Exponentialverteilung handelt es sich um eine stetige Verteilung, die häufig verwendet wird, um die erwartete Zeit bis zum Eintreten eines Ereignisses zu messen. In der Physik findet sie unter anderem bei der Messung des radioaktiven Zerfalls Anwendung.

Die F-Verteilung wurde entwickelt, um das Verhalten zweier Varianzen aus Zufallsstichproben zu untersuchen, die aus zwei unabhängigen Normalpopulationen entnommen wurden, denn bei Untersuchungen dieser Art ist es auf der Grundlage der Antworten der Zufallsstichproben unter anderem von Interesse, ob die Varianzen der Population identisch sind oder nicht. Hierbei findet die von Fisher entwickelte Verteilung Anwendung.

Die Gamma-Verteilung ist eine kontinuierliche Verteilung mit zwei positiven Parametern α und β. Ihre Bedeutung liegt vor allem in ihrer Beziehung zu Exponential- und Normalverteilungen. Gamma-Verteilungen finden häufig Anwendung in Modellen, die in der Technik, der Meteorologie sowie in der Wirtschaft (Versicherungsansprüche, Kreditausfälle) verwendet werden

Die Laplace-Verteilung ergibt sich auf natürliche Weise als die Verteilung der Differenz zweier unabhängiger, identisch verteilter Exponentialvariablen. Sie wurde nach Pierre Simon Laplace benannt. Da sie die Form zweier aneinandergereihter Exponentialverteilungen besitzt, wird sie auch als Doppelexponentialverteilung oder zweiseitige Exponentialverteilung bezeichnet.

Die logistische Verteilung ist eine stetige Verteilungsfunktion, welche unter anderem zur Beschreibung von Wachstumsprozessen mit einer Sättigungstendenz Anwendung findet. Sie besitzt breitere Ausläufer als die Normalverteilung, so dass sie besser mit den zugrunde liegenden Daten übereinstimmt und einen besseren Einblick in die Wahrscheinlichkeit von Extremereignissen bietet.

Die Gaußsche Normalverteilung ist eine Wahrscheinlichkeitsverteilung, die symmetrisch um den Mittelwert μ ist und zeigt, dass Daten in der Nähe des Mittelwerts häufiger vorkommen als Daten, die sich weit vom Mittelwert entfernt befinden. In grafischer Form wird die Normalverteilung als Glockenkurve dargestellt.

Die Standardnormalverteilung ist ein Spezialfall der Gaußschen Normalverteilung mit μ = 0 und σ²= 1. Da es häufig notwendig ist, Daten vor deren Analyse zu normalisieren findet diese Verteilung hierbei Anwendung.

Die Pareto-Verteilung ist eine schiefe Verteilung, die bisweilen zur Modellierung der Verteilung von Einkommen und anderen finanziellen Variablen verwendet wird.

Die Student-t-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung, die häufig in der Statistik Anwendung findet. Verteilungen dieser Art haben eine höhere Kurtosis als Normalverteilungen. Die Wahrscheinlichkeit, Werte zu erhalten, die sehr weit vom Mittelwert entfernt sind, ist bei einer derartigen Verteilung größer als bei einer Normalverteilung. T-Tests werden in der Statistik zur Schätzung der Signifikanz verwendet. T-Werte hängen vom Signifikanzniveau sowie von einer Stichprobengröße ab und bestimmen das Vertrauensintervall und hierdurch die Aussagekraft der Schätzung eines Mittelwertes.

Bei der Dreiecksverteilung (oder Simpsonverteilung) es sich um eine kontinuierliche Wahrscheinlichkeitsverteilung mit einer unteren Grenze a, einem Modus c sowie einer oberen Grenze b. Sie wird oftmals eingesetzt, wenn die Verteilung nur ungenau bekannt ist, aber wie bei der Gleichverteilung Ober- und Untergrenze bekannt sind, Sie wird bei der unternehmerischen Entscheidungsfindung und Projektplanung verwendet.

Die Uniform-Verteilung oder Gleichverteilung (Rechteckverteilung) ist die einfachste stetige Wahrscheinlichkeitsverteilung. Sie befasst sich mit Ereignissen, deren Auftreten gleich wahrscheinlich ist und besitzt in einem Intervall [a,b] eine konstante Wahrscheinlichkeitsdichte. Die Gleichverteilung einer Zufallsvariablen liegt vor, wenn jeder ihrer Werte die selbe Wahrscheinlichkeit besitzt. Eine diskrete Gleichverteilung liegt vor, wenn die Anzahl möglicher Ereignisse abzählbar ist, andernfalls handelt es sich um eine stetige Verteilung (stetige Gleichverteilung).

Die Weibull-Verteilung ist eine kontinuierliche Wahrscheinlichkeitsverteilung. Wie die Normalverteilung beschreibt die Weibull-Verteilung die Wahrscheinlichkeiten, die mit kontinuierlichen Daten verbunden sind. Im Gegensatz zur Normalverteilung kann sie jedoch auch schiefe Daten modellieren. Ihre extreme Flexibilität erlaubt es ihr, sowohl links- als auch rechtsschiefe Daten zu modellieren.

Eine negative Binomialverteilung ist die Verteilung der Summe unabhängiger geometrischer Zufallsvariablen. Sie beschreibt die Wahrscheinlichkeitsverteilung der Anzahl der Erfolge und Misserfolge die in einer Folge unabhängig voneinander durchgeführter Versuche vorliegt, bevor eine bestimmte Anzahl von Erfolgen eintritt.

Die Maxwell-Boltzmann-Verteilung ist eine Wahrscheinlichkeitsverteilung, die zur Beschreibung der Geschwindigkeiten verschiedener Teilchen in einem stationären Behälter bei einer bestimmten Temperatur Einsatz findet. Sie spielt in der Thermodynamik, insbesondere id der kinetischen Gastheorie, eine große Rolle

Mathematische Zusammenhänge - Formeln - Übersicht

Nachfolgend sind die Formeln und mathematischen Zusammenhänge der in diesem Unterprogramm zur Verfügung stehenden Verteilungsarten aufgeführt.

Beta-Verteilung:

Dichte:

f(x,a,b) = x^a-1(1-x)^b-1/B(a,b)

Verteilung:

F(x,a,b) = I_x(a,b)

mit:

a,b: Parameter (a > 0, b > 0)

B(a,b): Beta-Funktion

I_x(a,b): regularisierte unvollständige Betafunktion

x: Zufallsgröße

Cauchy-Verteilung:

Dichte:

Verteilung:

x₀,γ: Parameter (γ > 0)

x: Zufallsgröße

Chi²-Verteilung:

Dichte:

Verteilung:

n: Freiheitsgrad (n ≤ 0)

x: Zufallsgröße

Exponentialverteilung:

Dichte:

Verteilung:

λ: Parameter (λ > 0)

x: Zufallsgröße

F-Verteilung (Fisher-Verteilung):

Dichte:

Verteilung:

mit:

m,n: Freiheitsgrade (m > 0, n > 0)

x: Zufallsgröße

Gamma-Verteilung:

Dichte:

Verteilung:

k,f: Parameter (k > 0, φ > 0)

x: Zufallsgröße

Laplace-Verteilung:

Dichte:

Verteilung:

μ,b: Parameter (b > 0)

x: Zufallsgröße

Logistische-Verteilung:

Dichte:

Verteilung:

μ,s: Parameter (s > 0)

x: Zufallsgröße

Logarithmische-Normalverteilung:

Dichte:

Verteilung:

mit:

Logarithmiache Normalverteilung - Gleichung - 3

μ,σ: Parameter (σ > 0)

x: Zufallsgröße

Gaußsche Normalverteilung:

Dichte:

Verteilung:

mit:

μ,s: Parameter (σ² > 0)

x: Zufallsgröße

Standard-Normalverteilung (Normierte Normalverteilung):

Dichte:

Verteilung:

mit:

Standard-Normalverteilung- Gleichung - 3

x: Zufallsgröße

Pareto-Verteilung:

Dichte:

Verteilung:

k,x_m: Parameter (k > 0, x_m > 0)

x: Zufallsgröße

Student-t-Verteilung:

Dichte:

Verteilung:

mit:

n: Freiheitsgrade (n > 0)

x: Zufallsgröße

Dreiecksverteilung:

Dichte:

Verteilung:

a,b,c: Parameter (a < b, a < c < b)

x: Zufallsgröße

Uniform-Verteilung (Gleichverteilung):

Dichte:

Verteilung:

a,b: Parameter

x: Zufallsgröße

Weibull-Verteilung:

Dichte:

Verteilung:

λ,k: Parameter (λ > 0, k > 0)

x: Zufallsgröße

Negative Binomialverteilung:

Dichte:

Verteilung:

mit:

Negative Binomialverteilung - Gleichung - 4

Negative Binomialverteilung - Gleichung - 5

k,r: Parameter (k ∈ {0,1,3...}, r > 0)

x: Zufallsgröße

Maxwell Verteilung:

Dichte:

Verteilung:

mit:

a: Parameter (a > 0)

x: Zufallsgröße

Weitere Screenshots zu diesem Modul

MathProf - Beta-Verteilung - Dichtefunktion - Verteilungsfunktion - Quantile - Tabelle - Dichte - Verteilung - Beispiel - Berechnen - Plotten - Graph - Rechner - Darstellen
Grafische Darstellung - Beispiel 1 - Beta-Verteilung

MathProf - Cauchy-Verteilung - Dichtefunktion - Verteilungsfunktion - Quantile - Tabelle - Cauchy-Verteilung - Dichte - Verteilung - Beispiel - Wahrscheinlichkeitsdichte - Berechnen - Plotten - Graph - Rechner - Darstellen
Grafische Darstellung - Beispiel 2 - Cauchy-Verteilung

MathProf - Chi-Quadrat-Verteilung - Dichtefunktion - Verteilungsfunktion - Quantile - Tabelle - Chi-Quadrat -Verteilung - Dichte - Verteilung - Beispiel - Freiheitsgrad - Plotten - Graph - Berechnen - Rechner - Darstellen
Grafische Darstellung - Beispiel 3 - Chi ² - Verteilung

Grafische Darstellung - Beispiel 4 - Exponentialverteilung

MathProf - F-Verteilung - Dichtefunktion - Verteilungsfunktion - Wahrscheinlichkeitsfunktion - Quantile - Tabelle - Dichte - Verteilung - Beispiel - Plotten - Graph - Berechnen - Rechner - Darstellen- Sigma - Phi - Sigma - 0,9 - 0,95 - 0,975 - 0,99 - 0,995 - 0,1 - 0,05 - 0,025 - 0,01 - 0,005 - p Wert - p Werte
Grafische Darstellung - Beispiel 5 - F-Verteilung

MathProf - Gamma-Verteilung - Dichtefunktion - Verteilungsfunktion - Quantile - Tabelle - Gamma-Verteilung - Dichte - Verteilung - Beispiel - Parameter - Plotten - Graph - Berechnen - Rechner - Darstellen - Verteilungsdichte - Verteilungsdiagramm
Grafische Darstellung - Beispiel 6 - Gamma-Verteilung

MathProf - Laplace-Verteilung - Dichtefunktion - Quantile - Tabelle - Dichte - Verteilung - Beispiel - Wahrscheinlichkeitsdichte - Plotten - Berechnen - Graph - Rechner - Darstellen - Eigenschaften - Zufallsvariablen - Berechnung
Grafische Darstellung - Beispiel 7 - Laplace-Verteilung

MathProf - Logistische Verteilung - Dichtefunktion - Verteilungsfunktion - Wahrscheinlichkeitsfunktion - Quantile - Tabelle - Dichte - Verteilung - Beispiel - Wahrscheinlichkeitsdichte - Plotten - Berechnen - Graph - Rechner - Darstellen
Grafische Darstellung - Beispiel 8 - Logistische Verteilung

MathProf - Logarithmische Normalverteilung - Dichtefunktion - Quantile - Tabelle - Dichte - Verteilung - Beispiel - Plotten - Berechnen - Graph - Rechner - Darstellen
Grafische Darstellung - Beispiel 9 - Logarithmische Normalverteilung

MathProf - Gaußsche Normalverteilung - Normalverteilt - Dichtefunktion - Verteilungsfunktion - Wahrscheinlichkeitsfunktion - Quantile - Tabelle - Dichte - Verteilung - Beispiel -Parameter - Plotten - Berechnen - Graph - Rechner - DarstellenNormalverteilungskurve - PDF - CDF - NormCDF - NormalCDF - NormalPDF - Kumulierte Normalverteilung - Standardnormalverteilung - Normalverteilungskurve
Grafische Darstellung - Beispiel 10 - Gaußsche Normalverteilung

MathProf - Standard-Normalverteilung - Dichtefunktion - Quantile - Tabelle - Dichte - Verteilung - Beispiel - Berechnen - Plotten - Graph - Rechner - Darstellen
Grafische Darstellung - Beispiel 11 - Standard-Normalverteilung

MathProf - Pareto-Verteilung - Dichtefunktion - Verteilungsfunktion - Quantile - Tabelle - Dichte - Verteilung - Beispiel - Parameter - Plotten - Berechnen - Graph - Rechner - Darstellen
Grafische Darstellung - Beispiel 12 - Pareto-Verteilung

MathProf - Student-t-Verteilung - t-Verteilung - Dichtefunktion - Verteilungsfunktion - Quantile - Tabelle - Dichte - Verteilung - Beispiel - Berechnen - Freiheitsgrad - Plotten - Graph - Rechner - Darstellen
Grafische Darstellung - Beispiel 13 - Student-t-Verteilung

MathProf - Dreiecksverteilung - Dichtefunktion - Verteilungsfunktion - Quantile - Tabelle - Dichte - Verteilung - Beispiel - Berechnen - Parameter - Plotten - Graph - Rechner - Darstellen
Grafische Darstellung - Beispiel 14 - Dreiecksverteilung

MathProf - Uniform-Verteilung - Gleichverteilung - Dichtefunktion - Verteilungsfunktion - Quantile - Tabelle - Dichte - Verteilung - Beispiel - Parameter - Berechnen - Plotten - Graph - Rechner - Darstellen
Grafische Darstellung - Beispiel 15 - Uniform-Verteilung (Gleichverteilung)

MathProf - Weibull-Verteilung - Dichtefunktion - Verteilungsfunktion - Quantile - Tabelle - Dichte - Verteilung - Beispiel - Parameter - Berechnen - Plotten - Graph - Rechner - Darstellen
Grafische Darstellung - Beispiel 16 - Weibull-Verteilung

MathProf - Negative Binomialverteilung - Dichtefunktion - Verteilungsfunktion - Quantile - Tabelle - Dichte - Verteilung - Beispiel - Parameter - Berechnen - Plotten - Graph - Rechner - Darstellen
Grafische Darstellung - Beispiel 17 - Negative Binomialverteilung

MathProf - Maxwell-Verteilung - Dichtefunktion - Verteilungsfunktion - Quantile - Tabelle - Dichte - Verteilung - Beispiel - Paramater - Berechnen - Plotten - Graph - Rechner - Darstellen
Grafische Darstellung - Beispiel 18 - Maxwell-Verteilung

MathProf - F-Verteilung - Freiheitsgrad - Parameter - Dichte - Verteilung - Beispiel - Berechnen - Plotten - Graph - Rechner - Darstellen
Grafische Darstellung - Beispiel 19 - F-Verteilung

Screenshots und Kurzbeschreibungen einiger Module zu entsprechenden Themenbereichen

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.

Nützliche Infos zu diesem Themengebiet

Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.

Wikipedia - Normalverteilung
Wikipedia - Studetische t-Verteilung

Wikipedia - F-Verteilung
Wikipedia - Beta-Verteilung
Wikipedia - Cauchy-Verteilung
Wikipedia - Chi-Quadrat-Verteilung
Wikipedia - Exponentialverteilung
Wikipedia - Gammaverteilung
Wikipedia - Laplace-Verteilung
Wikipedia - Logistische Verteilung
Wikipedia - Logarithmische Normalverteilung
Wikipedia - Pareto-Verteilung
Wikipedia - Uniformverteilung
Wikipedia - Weibull-Verteilung
Wikipedia - Maxwell-Verteilung

Weitere implementierte Module zum Themenbereich Stochastik

Kombinatorik - Urnenmodell - Pfadregel - Galton-Brett - Statistische Messwertanalyse - Hypothesentest - Binomialverteilung - Binomialverteilung - Interaktiv - Binomialkoeffizienten - Geometrische Verteilung - Geometrische Verteilung - Interaktiv - Poisson-Verteilung - Poisson-Verteilung - Interaktiv - Hypergeometrische Verteilung - Hypergeometrische Verteilung - Interaktiv - Glockenkurve - Regressionsanalyse - Stichproben - Stichproben - Verteilungen - Lottosimulation - Vierfeldertest - Bedingte Wahrscheinlichkeit - Zusammenhang von Messwerten - Experimente - Gesetz der großen Zahlen - Berechnung von Pi (Monte-Carlo-Methode)

Screenshot des Startfensters dieses Moduls

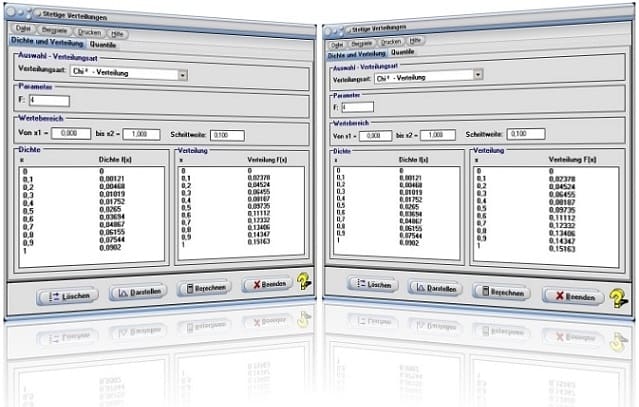
Startfenster des Unterprogramms Stetige Verteilungen

Screenshots weiterer Module von MathProf

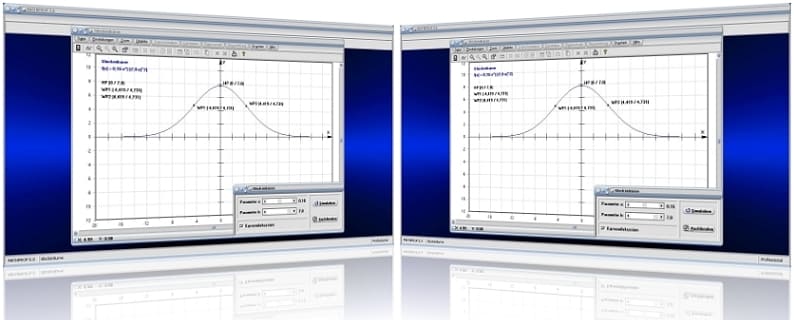
MathProf 5.0 - Unterprogramm Gaußsche Glockenkurve

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

Screenshot eines Moduls von PhysProf

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

Screenshot einer mit SimPlot erstellten Animationsgrafik

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke

MathProf 5.0 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich mathematische Sachverhalte auf einfache Weise zu verdeutlichen. Zudem spricht es diejenigen an, die sich für Mathematik interessieren, oder mathematische Probleme verschiedenster Art zu lösen haben und von grafischen 2D- und 3D-Echtzeitdarstellungen sowie Animationen beeindruckt sind.

Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.

Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.

Kurzinfos zu Inhalten einiger Unterprogramme erhalten Sie unter:

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Analysis eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Vektoralgebra eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

II - PhysProf 1.1
Physik interaktiv

PhysProf 1.1 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich physikalische Gesetzmäßigkeiten und Gegebenheiten zu verdeutlichen. Es spricht alle an, die sich für die Ergründung physikalischer Prozessabläufe und derartige Zusammenhänge interessieren. In zahlreichen Unterprogrammen besteht die Möglichkeit, Veränderungen von Einflussgrößen manuell, oder durch die Ausgabe automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren. Inhaltlich umfasst es ca. 70 verschiedene Unterprogramme zu den Fachthemenbereichen Mechanik, Elektrotechnik, Thermodynamik und Optik.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

III - SimPlot 1.0
Visualisierung und Simulation interaktiv

SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.

Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.

SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.

Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.

Eine Inhaltsübersicht dessen finden Sie unter SimPlot - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

Beispiele einiger mit Simplot 1.0 erzeugter Grafiken finden Sie unter Beispiele, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen mit SimPlot erzeugten Animationen finden Sie unter SimPlot-Videos, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

Zur Inhaltsseite

Zurück