MathProf - Punkte - 3D - Kartesisches 3D-Koordinatensystem - Diagramm
Fachthema: Punkte im Raum
MathProf - Geometrie - Programm für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.
Online-Hilfe
für das Modul zur Darstellung einfacher Punktgebilde im Raum durch Festlegung der Raumkoordinaten erforderlicher Punkte in einem kartesischen dreidimensionalen Koordinatensystem.
Nach der Festlegung der Raumkoordinaten erforderlicher Punkte und dem Berechnen notwendiger Werte, erfolgt deren Ausgabe in den entsprechenden Oktanten.
Neben dem Plotten von Punktgebilden kann in diesem Teilprogramm auch die Darstellung zusätzlicher Koordinatenebenen sowie benutzerdefinierter Ebenen in Koordinatenform im dreidimensionalen Raum veranlasst werden.
Ein frei bewegbares und drehbares, dreidimensionales Raummodell mit x-, y- und z-Achse ermöglicht die Durchführung interaktiver Analysen bzgl. den vorliegenden Sachverhalten und Zusammenhängen zu diesem Fachthema sowie zur Koordinatengeometrie im Raum.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben, sind implementiert.
Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.
Themen und Stichworte zu diesem Modul:Räumliches Koordinatensystem - Koordinaten im Raum - Räumliche Koordinaten - Punkt im Raum - Punkte im Raum - Raumkoordinaten - Räumliche Darstellung - Raum - Orientierung im Raum - 3D-Raum - 3D Daten - 3D Koordinaten - 3D Koordinatensystem - Dreidimensionaler Raum - Koordinatengeometrie - Oktanten - Dreidimensionales Koordinatensystem - 3 dimensionales Koordinatensystem - Bild - Grafik - x y z Koordinaten - Punktmengen - Herleitung - Beweis - Graph - Tabelle - Plotten - Räumlich - R3 - Raummodell - Begriff - Begriffe - Achsen - Koordinaten - Koordinatenachsen - X-Achse - Y-Achse - Z-Achse - Plotter - Punkte - Dreidimensional - 3D - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Einführung - Übungsaufgaben - Üben - Übungen - Aufgaben - Beispiel - Aufgabe - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Mathe - Mathematik - Zeichnen - Darstellen - Grafisch - Punkte plotten - Bilder - Darstellung - Koordinatenebene im Raum |
Selfbuild - Punkte im Raum
Modul Selfbuild - Punkte
Das kleine Unterprogramm [Geometrie] - [Sonstiges(3D)] - Selfbuild - Punkte ermöglicht die Darstellung von Punkten im Raum.
Unter dem Begriff dreidimensionaler Raum (3D-Raum) wird eine geometrische Umgebung verstanden, in welcher genau drei Werte notwendig sind, um die Position eines Punktes eindeutig zu bestimmen. Hierbei handelt es sich um die informelle Bedeutung des Begriffs Dimension.
In der Koordinatengeometrie ist ein Punkt als eine exakte Ortsangabe definiert. Um die Lage eines Punktes in diesem Raum eindeutig zu beschreiben, wird ein Koordinatensystem mit drei Achsen verwendet. Ein Punkt im Raum wird mittels seiner Koordinaten der Form (x,y,z) definiert.
Ein räumliches Koordinatensystem ermöglicht es, jedem seiner darin enthaltenen Punkte ein eindeutiges Zahlentripel zuzuordnen, welche als Koordinaten im Raum oder 3D-Koordinaten bezeichnet werden. In einem räumlichen Koordinatensystem ist es somit möglich, jedem Punkt P des Raums exakte Koordinaten zuzuordnen. Umgekehrt betrachtet, besitzt somit jeder Punkt P dieses Raums exakte Koordinaten der Form P(x,y,z), welche als Raumkoordinaten, Koordinaten im Raum oder räumliche Koordinaten bezeichnet werden.
Der Raum R3 wird durch das 3D-Koordinatensystem in acht Oktanten unterteilt. Die Koordinatenachsen des Systems sind gemäß dem mathematisch positiven Drehsinn angeordnet. Ihre Bezeichnungen lauten: X-Achse, Y-Achse und Z-Achse. Ein räumliches Koordinatensystem wird auch als dreidimensionales Koordinatensystem (3-dimensionales Koordinatensystem) bezeichnet.
Die Anordnung der drei Achsen des 3D-Koordinatensystems erfolgt gemäß dem mathematisch positiven Drehsinn. Die Skalierung beginnt im Ursprung des Systems und verläuft in die jeweils positive und negative Richtung. Nachfolgend aufgeführt ist eine Tabelle, die die Vorzeichen der einzelnen Oktanten angibt.
| I | II | III | IV | V | VI | VII | VIII | |
| X | + | - | - | + | + | - | - | + |
| Y | + | + | - | - | + | + | - | - |
| Z | + | + | + | + | - | - | - | - |
Screenshots
Grafische Darstellung - Beispiel 1
Grafische Darstellung - Beispiel 2
Grafische Darstellung - Beispiel 3
Darstellung
Um sich mit Hilfe dieses Moduls Punkte im Raum darstellen zu lassen, sollten Sie Folgendes ausführen:
- Geben Sie die Koordinatenwerte eines Punktes in die hierfür vorgesehenen Felder X, Y, Z ein und bedienen Sie die Schaltfläche Übernehmen.
- Wiederholen Sie diesen Vorgang bis alle erforderlichen Punkte aufgenommen sind.
- Möchten Sie einen Eintrag in der Tabelle löschen, so fokussieren Sie diesen und bedienen die Schaltfläche Löschen. Soll ein bereits eingetragener Wert geändert werden, so fokussieren Sie zunächst den entsprechenden Eintrag in der Tabelle, geben die neuen Koordinatenwerte in die entsprechenden Felder ein und bedienen hierauf die Schaltfläche Ersetzen. Um alle Einträge zu löschen, kann die Schaltfläche Alle löschen verwendet werden.
- Das Programm ermöglicht ein statisches Zooming des erstellten Gebildes durch die Definition eines entsprechenden Faktors. Diesen legen Sie durch die Eingabe eines gewünschten Werts in das Feld mit der Bezeichnung Darstellungsbereich wählen fest (dieser muss stets ³ 1 sein).
- Legen Sie den Durchmesser darzustellender Punkte durch die Bedienung des hierfür zur Verfügung stehenden Steuerelements Punktgröße fest. Soll eine Beschriftung der Punkte erfolgen, so aktivieren Sie zusätzlich das Kontrollkästchen Punkte beschriften. Um die Koordinatenwerte definierter Punkte bei der Darstellung auszugeben, aktivieren Sie das Kontrollkästchen Koordinaten.
- Sollen darzustellende Punkte durch Strecken verbunden werden, so aktivieren Sie das Kontrollkästchen Punkte verbinden. Um vertikale Strecken einblenden zu lassen, welche von den Punkten zur (x,y)-Ebene verlaufen, aktivieren Sie das Kontrollkästchen Vert. Strecken.
- Bedienen Sie die Schaltfläche Darstellen.
Alle Einträge werden durch eine automatisch ablaufende Nummerierung gekennzeichnet (Punkt Pn). Beim Löschen eines Eintrags wird diese nicht aktualisiert. Wollen Sie, dass die Nummerierung stets bei jeder Änderung von Einträgen aktualisiert wird, so aktivieren Sie das Kontrollkästchen Autom. Neunummerierung. Möchten Sie dies hingegen nur in einem konkreten Bedarfsfall durchführen, so bedienen Sie die Schaltfläche Nummerieren.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Mathe-Awendungsaufgaben genutzt werden.
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Datenverwaltung
Möchten Sie eingegebene Koordinatenwerte speichern, so kann dies über den Menüeintrag Datei - Speichern durchgeführt werden. Um die Daten bereits gespeicherter Darstellungen wieder zu verwenden, benutzen Sie den Menüeintrag Datei - Öffnen. Beim Öffnen einer Datei werden bereits eingegebene Werte durch die Dateidaten überschrieben!
Es besteht auch die Möglichkeit die Koordinatenwerte der Punkte in einer Excel-Tabelle zu definieren. Die Zahlenwerte sind nach folgendem Schema in der Excel-Tabelle festzulegen:
In Spalte A der Excel-Tabelle legen Sie die Werte für die X-, in Spalte B die Y- und in Spalte C die Z-Koordinaten der Punkte fest. Beginnen Sie mit der Eingabe in den obersten Feldern der entsprechenden Spalten.
Speichern Sie diese Tabelle hierauf in einer Datei ab. Bei Bedarf wählen Sie im Programm den Menüeintrag Datei - Excel-Daten importieren und öffnen die entsprechende Datei. Eingelesen werden alle Werte bis zum ersten leeren Feld der Excel-Tabellen-Spalte.
Allgemein
Grundlegendes zum Umgang mit dem Programm bei der Ausgabe dreidimensionaler grafischer Darstellungen erfahren Sie unter Dreidimensionale Grafiken - Handling. Wie Sie das Layout einer 3D-Darstellung konfigurieren können, erfahren Sie unter 3D-Layoutkonfiguration.
Weitere Themenbereiche
Beispiel
Um sich ein Bild der räumlichen Lage der Punkte A (-1 / -1 / -1), B (-1 / 1 / 1), C (1 / 1 / 1) und D (1 / -1 / -1) zu verschaffen, geben Sie in die zur Verfügung stehenden Felder aufeinanderfolgend die Koordinaten
| X: -1 |
| Y: -1 |
| Z: -1 |
| X: -1 |
| Y: 1 |
| Z: 1 |
| X: 1 |
| Y: 1 |
| Z: 1 |
| X: 1 |
| Y: -1 |
| Z: -1 |
ein und bestätigen jede Eingabe mit Übernehmen. Lassen Sie das Kontrollkästchen Darstellungsbereich wählen aktiviert und geben Sie in das daneben angeordnete Feld beispielsweise den Wert 1,5 ein. Bedienen Sie hierauf die Schaltfläche Darstellen, so können Sie sich ein Bild der räumlichen Lage der (rechteckförmig angeordneten) Punkte verschaffen.
Grafische Darstellung - Beispiel 4
Grafische Darstellung - Beispiel 5
Grafische Darstellung - Beispiel 6
Grafische Darstellung - Beispiel 7
Grafische Darstellung - Beispiel 8
Grafische Darstellung - Beispiel 9
Grafische Darstellung - Beispiel 10
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Achsenabschnittsform einer Geraden - Punkt-Richtungs-Form einer Geraden - Zwei-Punkte-Form einer Geraden - Hessesche Normalenform einer Geraden - Allgemeine Form einer Gerade - Gerade - Gerade - Gerade - Gerade - Interaktiv - Gerade - Punkt - Gerade - Punkt - Interaktiv - Geradensteigung - Kreis - Punkt - Kreis - Punkt - Interaktiv - Kreis - Gerade - Kreis - Gerade - Interaktiv - Kreis - Kreis - Kreis - Kreis - Interaktiv - Kreisausschnitt - Kreissegment - Kreisring - Ellipse - Regelmäßiges Vieleck - Viereck - Allgemeines Viereck – Interaktiv - Satz des Ptolemäus - Satz des Arbelos - Pappus-Kreise - Archimedische Kreise - Hippokrates Möndchen - Varignon-Parallelogramm - Rechteck-Scherung - Soddy-Kreise - Polygone - Bewegungen in der Ebene - Affine Abbildung - Analyse affiner Abbildungen - Inversion einer Geraden am Kreis - Inversion eines Kreises am Kreis - Spirolateralkurven - Spiralen im Vieleck - Granvillesche Kurven - Bérard-Kurven - Eikurven - Kegelschnitt - Prinzip - Pyramidenschnitt - Prinzip - Kegelschnitte in Mittelpunktlage - Kegelschnitte in Mittelpunktlage - Interaktiv - Kegelschnitte in achsparalleler Lage - Kegelschnitte in achsparalleler Lage - Interaktiv - Kegelschnitte in Mittelpunktlage - Punkt - Kegelschnitte in Mittelpunktlage - Gerade - Allgemeine Kegelschnitte - Kegelschnitte durch 5 Punkte - Interaktive Geometrie mit Objekten - Winkelmaße - Strahlensatz - Teilungsverhältnis - Konstruktion einer Mittelsenkrechten - Konvexe Hülle - Dreieck - Pyramide - Quader im Raum (3D) - Krummflächig begrenzte Körper (3D) - Ebenflächig und krummflächig begrenzte Körper (3D) - Platonische Körper (3D) - Archimedische Körper (3D) - Spezielle Polyeder (3D) - Selfbuild - Strecken (3D)
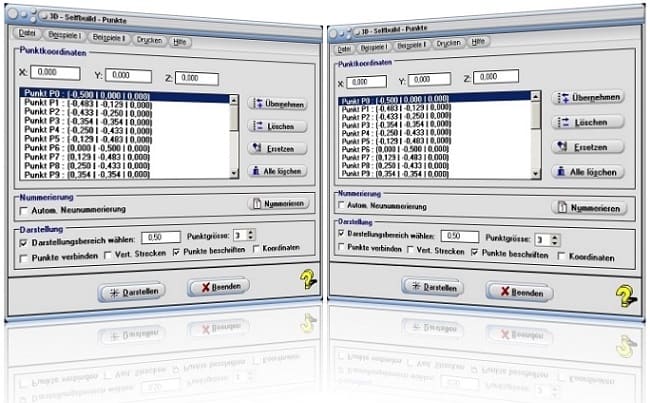
Startfenster des Unterprogramms Selfbuild - Punkte
MathProf 5.0 - Startfenster des Unterprogramms Strecken im Raum
MathProf 5.0 - Grafikfenster des Unterprogramms Kurven von Funktionen in Parameterform
PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Physik interaktiv
Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
- Kurzinfos zum Themengebiet Mechanik
- Kurzinfos zum Themengebiet Elektrotechnik
- Kurzinfos zum Themengebiet Optik
- Kurzinfos zum Themengebiet Thermodynamik
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
