MathProf - Potenzrechnung - Potenzgesetze - Potenzen - Quadrieren
Fachthemen: Schriftliche Potenzierung - Potenzgesetze - Potenzregeln - Exponenten
MathProf - Arithmetik - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für Schüler, Abiturienten, Studenten, Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.
Online-Hilfe
für das Modul zur Durchführung der schriftlichen Potenzierung.
Dieses kleine Unterprogamm ermöglicht das Üben sowie die praktische Anwendung des schriftlichen Potenzierens natürlicher Zahlen unter der Verwendung selbstdefinierbarer ganzer Zahlen.
Beispiele, welche Aufschluss über die Verwendbarkeit dieses
Programmmoduls geben, sind implementiert.
Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.
Themen und Stichworte zu diesem Modul:Schriftliches Potenzieren - Potenz - Potenzen - Gesetze - Potenzierung - Potenzrechnung - Potenzzahlen - Hochzahl - Basiszahl - Basis - Grundzahl - Exponent - Exponenten - Regel - Regeln - Umformungsregeln - Potenziert - Zahl - Zahlen - Zweierpotenz - Potenzwert - Potenzwerte - Dritte Potenz - Vierte Potenz - Fünfte Potenz - Rechner - Berechnen - Übersicht - Potenzgesetze - Hoch - Hoch 2 - Hoch 3 - Hoch 4 - Hoch 5 - Hoch minus - 0 als Potenz - Hoch 0 - Null hoch null - 2 hoch - 3 hoch - 4 hoch - 5 hoch - 6 hoch - 7 hoch - 8 hoch - 10 hoch - Unterschiedliche Exponenten - 0 als Exponent - Positive Potenzen - Negative Potenzen - Positive Basis - Negative Basis - Plus - Minus - Positiv - Negativ - Potenzen mit gleicher Basis - Potenzen mit gleichem Exponenten - Hoch null - Potenzturm - Zweierpotenzen - Zehnerpotenz - Zehnerpotenzen - Quadrieren - Quadratzahlen - Kubikzahlen - Von - Bis - 15 - 20 - 25 - 30 - Zweistellig - Dreistellig - Eigenschaften - Ergebnis - Liste - Tabelle - Potenzrechenregeln - Potenzen dividieren - Potenzen multiplizieren - Potenzregeln - Potenzieren - Potenzrechnen - Potenzen potenzieren - Potenzen addieren - Potenzen subtrahieren - Als Potenz schreiben - Schreibweise - Hoch minus - Rationale Exponenten - Positiver Exponent - Negativer Exponent - Gerade Potenzen - Ungerade Potenzen - Potenzen mit negativen Exponenten - Potenzen mit negativer Basis - 2er Potenzen - 3er Potenzen - 10er Potenzen - Stufenzahl - Stufenzahlen - Rechnen mit Potenzen - Rechnen mit Exponenten - Rechnen mit Hochzahlen - Grundzahl - Grundlagen - 0 - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - ^ - Addition - Subtraktion - Multiplikation - Division - Differenz - Summe - Produkt - Quotient - Formeln - Potenzrechner - Zweite Potenz - Hoch minus eins - Potenzen von Potenzen - Brüche potenzieren - Negative Potenzen - Gleiche Basis - Gleiche Exponenten - Gleiche Potenzen - Potenzterm - Gleicher Exponent - Unterschiedliche Basis - Unterschiedliche Potenzen - Umkehroperation - Umkehrrechnung - Rechengesetze - Anwendung - Anwenden - Rechnen - Regeln - Rechenregeln - Umrechnen - Umrechnung - Grundlagen - Grundlegendes - Erklärung - Einfach erklärt - Mathe - Mathematik - Beschreibung - Definition - Rechengesetz - Bezeichnung - Bezeichnungen - Darstellen - Darstellung - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Einführung - Was - Wie - Weshalb - Was ist - Wie viel - Was sind - Welche - Welcher - Welches - Wodurch - Wie viele - Wieviel - Wie berechnet man - Begriff - Begriffe - Herleitung - Beweis - Bedeutung - Was bedeutet - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Potenzen vereinfachen - Potenzschreibweise - Zehnerpotenzschreibweise - Potenzterme - Umformen - Umformung - Potenzterme vereinfachen - Vereinfachen - Vereinfachung - Beispiele - Terme - Rechnen - Brüche in Potenzen - Geteilt - Hochzahlen - Gebrochene Exponenten - Kubikzahl - Exponentialgesetze - 1. Potenzgesetz - 2. Potenzgesetz - 3. Potenzgesetz - 4. Potenzgesetz - 5. Potenzgesetz - Negative Exponenten - Bruch - Potenzieren von Potenzen - Potenzieren von Brüchen - Vorzeichen |
Schriftliche Potenzierung - Potenzgesetze - Potenzregeln - Rechnen mit Potenzen - Potenzrechnen
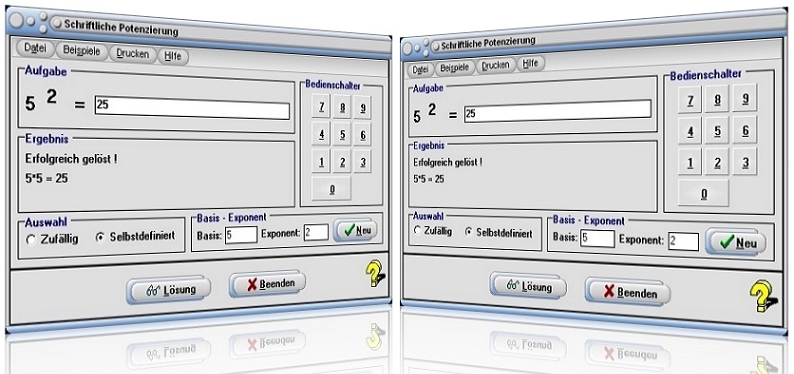
Modul Schriftliche Potenzierung
Das kleine Unterprogramm [Sonstiges] - [Arithmetik] - Schriftliche Potenzierung stellt eine Anwendung zur Verfügung, mit welcher es möglich ist, die Vorgehensweise zur Durchführung der schriftlichen Potenzierung zweier natürlicher Zahlen zu üben bzw. zu analysieren. Es wird das Erlernen der geltenden Potenzregeln und Potenzgesetze ermöglicht.
Abbildung 1 - Zufällige Aufgabe
Abbildung 2 - Selbstdefinierte Aufgabe
Als schriftliche Potenzierung (schriftlich potenzieren oder schriftliches Potenzieren) wird eine Rechenmethode bezeichnet, mithilfe derer die Potenzierung zweier mehrstelliger ganzahliger Werte durch eine schriftliche Darstellung praktiziert werden kann. Mit dem Begriff Potenzieren wird die Schreibweise für das mehrmalige aufeinanderfolgende Multiplizieren einer Zahl mit ihrer selbst beschrieben. Diese Rechenmethode wird auch als Potenzrechnung oder Potenzierung (seltener als Potenzrechnen) bezeichnet.
Sie kann in diesem Unterprogramm mit Hilfe des implementierten Potenzrechners durchgeführt werden und zur Lösung einfacher Aufgaben zu diesem Thema eingesetzt werden.
Programmbedienung
Gehen Sie folgendermaßen vor, um eine schriftliche Potenzierung mit Hilfe dieses Moduls durchzuführen:
- Wählen Sie im Formularbereich Auswahl durch die Aktivierung des Kontrollschalters Zufällig bzw. Selbstdefiniert, ob eine Aufgabe durch den programminternen Zufallsgenerator erzeugt werden soll, oder ob Sie eine selbstdefinierte Aufgabe erstellen möchten.
Wurde die Durchführung einer vom Programm zufällig erzeugten Aufgabe gewählt, so führen Sie einen Klick auf die Schaltfläche Neue Aufgabe aus, um dem Programm mitzuteilen, eine neue Aufgabe zu erstellen.
Möchten Sie selbst eine eigene Aufgabe vorgeben, so aktivieren Sie hierfür zunächst den Kontrollschalter Selbstdefiniert, geben die entsprechenden Zahlenwerte in die dafür vorgesehenen Felder Basis und Exponent ein und bedienen darauffolgend die Schaltfläche Neu.
- Klicken Sie hierauf auf die entsprechenden rechtsseitig angeordneten Bedienschalter, die mit Zahlensymbolen versehen sind, um dem Programm das Ergebnis Ihrer Berechnung mitzuteilen. Wird ein korrekt ermittelter Zahlenwert eingegeben, so wird dieser im Ergebnisfeld ausgegeben. Wird hingegen eine falsche Taste bedient, so wird der durchgeführte Klick auf das entsprechende Zahlensymbol ignoriert.
Nach einer erfolgreich durchgeführten Schalter- bzw. Tastaturbedienung wird der zuletzt durchgeführte Rechenschritt angezeigt.
Möchten Sie die Aufgabe vom Programm lösen lassen, so bedienen Sie die Schaltfläche Lösung. Das Programm bearbeitet daraufhin alle zu durchlaufenden Rechenschritte und gibt das Ergebnis der Berechnung aus. Durch eine Bedienung der Schaltfläche Beenden schließen Sie dieses Unterprogramm.
Hinweis:
Zahlenwerte können auch durch die Benutzung der entsprechenden Tastaturtasten eingegeben werden.
Potenzierung - Potenzieren - Potenz - Potenzen - Grundlagen - Bezeichnungen
Als Potenz wird die Schreibweise für die wiederholte Multiplikation des Faktors einer Zahl bezeichnet. Es gilt: x1·x2·x3 ... xn = xn.
Das Berechnen von Potenzen wird als Potenzieren bezeichnet. Es ist ein mehrfaches Multiplizieren mit einer Zahl. Zum Beispiel: 23 = 2·2·2. Der Wert einer Potenz ist der Potenzwert. Gerade Potenzen besitzen geradzahlige Exponenten und ungerade Potenzen besitzen ungeradzahlige Exponenten.
Mantisse: Die Mantisse einer Potenz beschreibt die Gleitkommazahl vor einer Potenz.
Potenzterme: Jeder Term, der in Form einer Potenz geschrieben ist, wird als Potenzterm bezeichnet. Beispiele für Potenzterme sind:
x²
(2+x)³
4^(2-2x)
Basis: Die Basis einer Potenz ist die Zahl, die mit sich selbst zu multiplizieren ist. Sie wird auch als Grundzahl oder Basiszahl bezeichnet.
Exponent (Hochzahl): Der Exponent (die Hochzahl) einer Potenz ist diejenige Zahl die beschreibt, wie häufig die Basiszahl mit sich selbst zu multiplizieren ist und den Grad einer Potenz wiedergibt. Jede Potenz mit dem Exponenten 0 ergibt 1.
Potenzzahl: Als Potenzzahl wird eine natürliche Zahl p bezeichnet, die in Form eines Produkts aus wenigstens zwei identischen Faktoren geschrieben werden kann.
Unterschiedliche Potenzen - Unterschiedliche Basis und unterschiedlicher Exponent:
Beim Vorhandensein zweier Potenzen mit unterschiedlicher Basis und unterschiedlichem Exponenten ist keine Rechenoperation mit diesen durchführbar.
Negative Basis - Positive Basis - Negativer Exponent - Negative Exponenten - Positiver Exponent: Die Potenz einer Zahl mit negativer Basis ist positiv, wenn deren Exponent gerade ist. Ist dieser ungerade, so ist die Potenz dieser Zahl negativ.
Dies bedeutet: Potenzen mit positiver Basis besitzen stets einen positiven Potenzwert. Potenzen mit negativer Basis und geradzahligem Exponenten besitzen positive Potenzwerte. Potenzen mit negativer Basis und ungeradzahligem Exponenten besitzen negative Potenzwerte.
Beispiele:
Positive Basis und gerader Exponent: 24 = 2·2·2·2 = 32
Positive Basis und ungerader Exponent: 25 = 2·2·2·2·2 = 64
Negative Basis und gerader Exponent: -24 = (-2)·(-2)·(-2)·(-2) = 32
Negative Basis und ungerader Exponent: -25 = (-2)·(-2)·(-2)·(-2)·(-2) = -64
Potenzgesetze - Regeln - Schreibweise - Übersicht
Potenzgesetze werden eingesetzt um das Rechnen mit Potenzen zu ermöglichen sowie Potenzen zu vereinfachen. Potenzgesetze werden auch als Potenzregeln (Potenzrechenregeln) bezeichnet. Nachfolgend aufgeführt sind die geltenden Potenzgesetze (Rechengesetze) sowie die entsprechenden Rechenregeln (Regeln zum Rechnen mit Potenzen).
| a0 = 1 | Potenz mit dem Exponenten 0, mit a ≠ 0 |
 | Potenz mit dem Exponenten 1 |
 | Multiplikation von Potenzen mit gleicher Basis (1. Potenzgesetz) |
 | Potenzierung von Potenzen (3. Potenzgesetz - Potenztürme) |
 | Multiplikation von Potenzen mit gleichem Exponenten (2. Potenzgesetz) |
 | Potenz mit negativem Exponenten (hoch minus) |
 | Division von Potenzen mit gleicher Basis (5. Potenzgesetz) |
 | Division von Potenzen mit gleichem Exponenten (4. Potenzgesetz) |
 | Potenz deren Exponent aus der Inversen einer natürlichen Zahl besteht |
 | Potenz deren Exponent aus einem Bruch besteht (Gebrochene Exponenten, Brüche in Potenzen bzw. Exponenten) |
Potenzen können nur dann addiert oder subtrahiert werden, wenn diese eine gemeinsame Basis sowie einen gemeinsamen Exponenten besitzen. Die Umkehroperation (Umkehrrechnung) des Potenzierens ist das Logarithmieren.
| axn+ bxn = (a+b)xn | Potenzen addieren |
| axn- bxn = (a-b)xn | Potenzen subtrahieren |
Zweierpotenz:
Zweierpotenzen (2er Potenzen) entstehen aus der mehrfachen Multiplikation der Grundzahl 2 mit sich selbst.
Beispiele: 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048 ...
Diese Zahlen können in Form von Zweierpotenzen ausgedrückt werden.
Beispiele: 2 = 21, 4 = 22, 8 = 23, 16 = 24, 32 = 25, 64 = 26, 128 = 27, 256 = 28 ....
Zehnerpotenz - Stufenzahl:
Zehnerpotenzen (auch als Stufenzahlen oder 10er Potenzen bezeichnet) entstehen aus der mehrfachen Multiplikation der Grundzahl 10 mit sich selbst.
Beispiele: 10, 100, 1000, 10000, 100000, 1000000 ....
Derartige Zahlen können in Form von Zehnerpotenzen ausgedrückt werden. Diese Darstellung wird als Potenzschreibweise oder Zehnerpotenzschreibweise bezeichnet.
Beispiele für die Zehnerpotenzschreibweise: 10 = 101, 100 = 102, 1000 = 103, 10000 = 104, 100000 = 105, 1000000 = 106 ....
Zehnerpotenzen werden auch als Stufenzahlen bezeichnet.
Hoch 0 - Hoch Null:
Eine beliebige Zahl oder Variable, die den Exponenten 0 besitzt (Zahl hoch 0) besitzt stets den Zahlenwert eins. Eine Ausnahme stellt die Zahl 0 dar. Ist diese zugleich als Basis sowie als Exponent vorhanden (Null hoch null bzw. 00), so ist der Wert dieser Zahl ist nicht definiert.
Dritte Potenz - Vierte Potenz - Fünfte Potenz: Die dritte Potenz ist das Resultat einer mathematischen Rechenoperation, bei der eine Zahl dreimalig aufeinanderfolgend mit sich selbst multipliziert wird. Analoges gilt für die vierte Potenz und die fünfte Potenz sowie jede n-te Potenz einer Zahl.
Potenzen quadrieren: Die Berechnung des Quadrats einer Zahl wird als Quadrieren bezeichnet. Hierbei erfolgt die Multiplikation dieser Zahl mit sich selbst.
Potenzen multiplizieren: Potenzen mit gleichen Basen werden multipliziert, indem ihre Exponenten addiert werden und ihre Basis beibehalten wird.
Potenzen dividieren: Potenzen mit gleichen Basen werden dividiert, indem ihre Exponenten subtrahiert werden und ihre Basis beibehalten wird.
Potenzieren von Potenzen: Potenzen werden potenziert, indem die Basis beibehalten wird und die Exponenten miteinander multipliziert. Ist die Basis negativ und besitzt der äußere Exponent einen geradzahligen Wert so entfällt das negative Vorzeichen der Basis.
Potenzen mit negativen Exponenten: Ist die Hochzahl im Zähler kleiner ist als die im Nenner, so führt eine Division von Potenzen mit gleicher Basis zu einer Potenz mit negativem Exponent. Beispiel: x3 : x5 = x3/x5 = xxx/xxxxx = 1/xx = 1/x2 = x3-5 = x-2
Quadratzahlen - Kubikzahlen
Quadratzahlen:
Quadratzahlen oder Zweierpotenzen werden alle Zahlen bezeichnet, welche durch die Multiplikation einer natürlichen Zahl mit sich selbst entstehen. Die ersten Quadratzahlen sind: 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121 ...
Nachfolgend ist die Liste (Tabelle) der ersten Quadratzahlen (positiver Zahlen) aufgelistet:
1 · 1 = 1
2 · 2 = 4
3 · 3 = 9
4 · 4 = 16
5 · 5 = 25
6 · 6 = 36
7 · 7 = 49
8 · 8 = 64
9 · 9 = 81
10 · 10 = 100
11 · 11 = 121
12 · 12 = 144
13 · 13 = 169
14 · 14 = 196
15 · 15 = 225
16 · 16 = 256
17 · 17 = 289
18 · 18 = 324
19 · 19 = 361
20 · 20 = 400
21 · 21 = 441
22 · 22 = 484
23 · 23 = 529
24 · 24 = 576
25 · 25 = 625
26 · 26 = 676
27 · 27 = 729
28 · 28 = 784
29 · 29 = 841
30 · 30 = 900
Kubikzahlen:
Als Kubikzahlen werden alle Zahlen bezeichnet, welche durch das Produkt dreier gleicher natürlicher Zahlen mit sich selbst entstehen. Die ersten Kubikzahlen sind: 0, 1, 8, 27, 64, 125, 216, 343, 512, 729, 1000, 1331 ...
Nachfolgend ist die Liste (Tabelle) der ersten Kubikzahlen (positiver Zahlen) aufgelistet:
1 · 1 · 1 = 1
2 · 2 · 2 = 8
3 · 3 · 3 = 27
4 · 4 · 4 = 64
5 · 5 · 5 = 125
6 · 6 · 6 = 216
7 · 7 · 7 = 343
8 · 8 · 8 = 512
9 · 9 · 9 = 729
10 · 10 · 10 = 1000
11 · 11 · 11 = 1331
12 · 12 · 12 = 1728
13 · 13 · 13 = 2197
14 · 14 · 14 = 2744
15 · 15 · 15 = 3375
Rechenoperationen mit Potenzen
Mit Potenzen können folgende Rechenoperationen durchgeführt werden:
- Potenzen addieren
- Potenzen subtrahieren
- Potenzen multiplizieren
- Potenzen dividieren
- Potenzen potenzieren
Potenzen addieren und Potenzen subtrahieren: Das Addieren und Subtrahieren von Potenzen kann lediglich mit Potenzen durchgeführt werden, die die gleiche Basis sowie den gleichen Exponenten besitzen. Die Voraussetzung zur Durchführung einer Addition oder einer Subtraktion zweier Potenzen lautet somit: Gleiche Basis und gleiche Exponenten.
Potenzen multiplizieren und Potenzen dividieren: Zur Durchführung einer Multiplikation oder Division mit Potenzen mussen folgende Bedingungen erfüllt sein:
Beide Zahlen besitzen die gleiche Basis
Beide Zahlen besitzen den gleichen Exponenten
Potenzgesetze
1. Potenzgesetz:
Potenzen addieren: Zwei Potenzen mit gleicher Basis werden multipliziert, indem deren Exponenten addiert werden und die gemeinsame Basis beibehalten wird.
Beispiel: 23 * 24 = 23+4 = 27 = 128
2. Potenzgesetz:
Potenzen dividieren: Zwei Potenzen mit gleicher Basis werden dividiert, indem deren Exponenten subtrahiert werden und die gemeinsame Basis beibehalten wird.
Beispiel: 25 : 24 = 25-4 = 21 = 2
3. Potenzgesetz:
Potenzen multiplizieren: Zwei Potenzen mit gleichem Exponenten werden multipliziert, indem deren Basis multipliziert wird und der gemeinsame Exponent beibehalten wird.
Beispiel: 23 * 43 = (2*4)3 = 83 = 512
4. Potenzgesetz:
Potenzen dividieren: Zwei Potenzen mit gleichem Exponenten werden dividiert, indem deren Basis dividiert wird und der gemeinsame Exponent beibehalten wird.
Beispiel: 22 : 32 = (2/3)2 = 4/9
5. Potenzgesetz:
Potenzen potenzieren: Zwei Potenzen werden potenziert, indem deren Exponenten multipliziert werden und die gemeinsame Basis beibehalten wird.
Beispiel: (23)3 = 23+3 = 26 = 64
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema in Mathe.
Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet der Mathematik, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Weitere Themenbereiche
Beispiel
Wurde der Kontrollschalter Selbstdefiniert aktiviert, wurden in die Felder Basis und Exponent die Zahlen 3 und 6 eingetragen und der Schalter Neu bedient, so gibt das Programm nach einer aufeinanderfolgenden Bedienung der Schaltflächen (oder Eingabetasten der Tastatur) 7, 2, 9 aus, dass die Aufgabe erfolgreich gelöst wurde, da eine Potenzierung der Zahl 3 mit der Zahl 6 die Zahl 729 ergibt.
Beispiel 1
Beispiel 2
Beispiel 3
Beispiel 4
Beispiel 5
Beispiel 6
Beispiel 7
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Potenzen sowie unter Wikipedia - Zehnerpotenz zu finden.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Zahlenstrahl - Römische Zahlen - Schriftliche Addition - Schriftliche Subtraktion - Schriftliche Multiplikation - Schriftliche Division - Aussagenlogik - Zahltypumwandlung - Zinsrechnung - Zinseszinsrechnung grafisch - Annuitätentilgung - Jahreszinsrechnung - Physikalische Größen - Materialkonstanten - Fachbegriffe Deutsch - Englisch - Mandelbrot- und Juliamengen - Zusammenhänge Mandelbrot-Juliamengen - Sierpinski-Dreieck - Koch-Kurve - Pythagoras-Baum - Feigenbaum-Diagramm - Lindenmayer-System - Lindenmayer-System II - Logistische Gleichung I - Logistische Gleichung II - Diagramme - Tortendiagramm - Kryptografie - Raumgittermodelle (3D) - Paare geordnet - Kalender - Rechnen mit selbstdefinierten Formeln - Zeichenprogramm - Tangram - Tetris - Spiel 15 - Türme von Hanoi - Dame - Schach
MathProf 5.0 - Unterprogramm Schriftliche Subtraktion
MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Physik interaktiv
Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
- Kurzinfos zum Themengebiet Mechanik
- Kurzinfos zum Themengebiet Elektrotechnik
- Kurzinfos zum Themengebiet Optik
- Kurzinfos zum Themengebiet Thermodynamik
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
