MathProf - Schriftliche Multiplikation - Einmaleins - 1x1

Fachthemen: Schriftliche Multiplikation - Schriftlich multiplizieren - Einmaleins
MathProf - Grundlagen der Mathematik - Arithmetik - Software für interaktive Schulmathematik zum Lösen verschiedenster Aufgaben, zur Anwendung grundlegender Rechenoperationen und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für Schüler, Abiturienten, Studenten und Lehrer sowie für alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Durchführung der schriftlichen Multiplikation zweier natürlicher Zahlen.
Dieses kleine Unterprogamm ermöglicht das Üben sowie die praktische Anwendung des schriftlichen Multiplizierens natürlicher Zahlen unter der Verwendung selbstdefinierbarer ganzer Zahlen.
Es zeigt den praktizierten Rechenweg sowie die zur Ermittlung der Lösung einer Aufgabe zur Bildung vom Produkt zweier Zahlen durchlaufenen Rechenschritte und unterstützt bei der Lösung entsprechender Rechenaufgaben.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben und dazu dienlich sind, Aufgaben zu diesem Themengebiet zu lösen, sind implementiert.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Schriftliches Multiplizieren - Schriftlich multiplizieren - Ganze Zahlen multiplizieren - Rechenverfahren - Rechenschritte - Rechenweg - Multiplizieren - Multiplikation - Multiplikationen - Multiplikationsaufgabe - Multiplikationsaufgaben - Ausmultiplizieren - Faktorisieren - Ausklammern - Mal rechnen - Faktor - Produkt - Berechnen - Rechner - Rechnen - Rechenvorgang - Kommaschreibweise - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Einführung - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Aufgabe - Hausaufgaben - Was ist - Wie viel - Wie viele - Wieviel - Wieviele - Welche - Welcher - Welches - Wodurch - Grundlagen - Bedeutung - Was bedeutet - Herleitung - Beweis - Erklärung - Einfach erklärt - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Darstellen - Darstellung - Übersicht - Grundrechenart - Mal - Multipliziert - Zahl - Zahlen - Große Zahlen - Ergebnis - Mathe - Mathematik - Rechengesetz - Vorzeichenregeln - Schriftlich mal rechnen - Multiplikation ganzer Zahlen - Multiplikator - Multiplikand - Kommazahlen multiplizieren - Dezimalzahlen multiplizieren - Dezimalzahl - Dezimalzahlen - Kommazahl - Kommazahlen - Komma - Rechenwege - Einstellig - Zweistellig - Dreistellig - Ergebnis - Verdoppeln - Verdopplung - Verdoppelung - Vielfache - Vielfaches - Neutrales Element - Inverses Element - Malaufgabe - Malaufgaben - Malnehmen - Multipliziere - Multpliziert mit - Mal - Klasse 1 - Klasse 2 - Klasse 3 - Klasse 4 - 1. Klasse - 2. Klasse - 3. Klasse - 4. Klasse - Erste Klasse - Zweite Klasse - Dritte Klasse - Vierte Klasse - Grundschule - 0 - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - 11 - 12 - 13 - 14 - 15 - 16 - 17 - 18 - 19 - 20 - * - Null - Eins - Zwei - Drei - Vier - Fünf - Sechs - Sieben - Acht - Neun - Zehn - Elf - Zwölf - Dreizehn - Vierzehn - Fünfzehn - Sechzehn - Siebzehn - Achtzehn - Neunzehn - Zwanzig - Dreißig - Vierzig - Fünfzig - Sechzig - Siebzig - Achtzig - Neunzig - Hundert - Tausend - Das Doppelte von - Das Zweifache von - Das Dreifache von - Das Vierfache von - Das Fünffache von - Das Sechsfache von - Das Siebenfache von - Das Achtfache von - Das Neunfache von - Das Zehnfache von - Zweifaches - Doppeltes - Dreifaches - Vierfaches - Fünffaches - Sechsfaches - Zehnfaches - Zweimal - Dreimal - Viermal - Fünfmal - Zwei mal - Drei mal - Vier mal - Fünf mal - Sechs mal - Sieben mal - Acht mal - Neun mal - Zehn mal - Lösungen - Lösen - Lösungsweg - Trainer - Trainieren - Begriff - Begriffe - Einmaleins - Kleines Einmaleins - Einmaleinsreihen - 1x1 - 1mal1 - 1 x 1 - 1 x - 2 x - 3 x - 4 x - 5 x - 1 mal 1 - Großes Einmaleins - Großes 1 mal 1 - Großes 1 x 1 - Tabelle - Tabellen - 2 x 2 - 2 x 3 - 3 x 2 - 4 x 2 - 2 x 4 - Multiplikationstabelle - Multiplikationstabellen - 1er Reihe - 2er-Reihe - 3er-Reihe - 4er-Reihe - 5er-Reihe - 6er-Reihe - 7er-Reihe - 8er-Reihe - 9er-Reihe - 10er-Reihe - Einerreihe - Zweierreihe - Dreiereihe - Vierereihe - Fünferreihe - Sechserreihe - Siebenrreihe - Achterreihe - Neunerreihe - Zehnerreihe - Malreihe - Malreihen - Malfolge - Malfolgen |
Schriftliche Multiplikation

Modul Schriftliche Multiplikation
Das kleine Unterprogramm [Sonstiges] - [Arithmetik] - Schriftliche Multiplikation stellt eine Anwendung zur Verfügung, mit welcher es möglich ist, die Vorgehensweise (den Rechenweg) zur Durchführung der schriftlichen Multiplikation zweier natürlicher Zahlen zu üben bzw. zu analysieren.

Als schriftliche Multiplikation (schriftliches Multiplizieren oder schriftlich Multiplizieren bzw. schriftlich mal rechnen) wird eine Rechenmethode bezeichnet, mithilfe derer die Multiplikation zweier mehrstelliger ganzer Zahlen durch eine schriftliche Darstellung praktiziert werden kann.
Sie kann in diesem Unterprogramm durchgeführt werden und zur Lösung einfacher Multiplikationsaufgaben (wie z.B. Verdopplungsaufgaben und sonstiger Malaufgaben) eingesetzt werden. Auch wird beim Durchführen von Multiplikationen der dabei durchlaufene Rechenweg aufgezeigt.
Die Multiplikation ist eine der vier Grundrechenarten in der Arithmetik und wird auch Malnehmen genannt. Als Multiplikator wird eine Zahl bezeichnet, mit der eine vorgegebene Zahl multipliziert wird. Die Zahl, die mit einer anderen zu multiplizieren ist heißt Multiplikand.
Nachbaraufgaben: Mit Hilfe des Rechnens von Nachbaraufgaben lassen sich bei der Ausführung der Grundrecharten gekonnt Aufgaben lösen. Beispielsweise kann bei der Berechnung der Aufgabe 5·199 die Multiplikatiion der Zahlen 5·200 durchgeführt werden und hierauf der Faktor 5·1 vom Ergebnis abgezogen werden. Bei einer Malaufgabe besitzt jede Rechenaufgabe eine Nachbaraufgabe.
Vorzeichenregel: Nachfolgend sind die geltenden Vorzeichenregeln aufgeführt, die bei der Durchführung einer Multiplikation beim Rechnen mit ganzen, rationalen und reellen Zahlen relevant sind. Es gilt:
- Ein Produkt aus zwei Faktoren mit gleichem Vorzeichen ist stets positiv.
- Ein Produkt aus zwei Faktoren mit unterschiedlichem Vorzeichen ist stets negativ.
Grundsätzlich gilt: Minus mal Plus ergibt Minus und Plus mal Minus ergibt Minus.
Eine Division kann in Form einer Multiplikation mit dem Kehrwert des Divisors geschrieben werden. Somit gelten die zuvor geln auch bei der Durchführung einer Division, wenn der Quotient keine Null ist.
Neutrales Element: Als neutrales Element wird eine Zahl (oder andere mathematische Sache) bezeichnet, die andere Zahlen bei der Ausführung einer mathematischen Operation unverändert lässt. Beispiele hierzu sind nachfolgend aufgeführt:
Bei einer Multiplikation ist die Zahl 1 ein neutrales Element, denn 1 · 4 = 4 bzw. a ⋅ 1 = a
Bei einer Addition ist die Zahl 0 ein neutrales Element, denn 0 + 5 = 5
Bei einer Subtaktion ist die Zahl 0 ein neutrales Element, denn 7 - 0 = 7
Inverses Element: Als inverses Element wird eine Zahl bezeichnet, die die folgende Eigenschaft besitzt: Wird ein beliebiges Element (eine beliebige Zahl) mit diesem inversen Element verknüpft, so resultiert hieraus das jeweilige neutrale Element. Ein inverses Element existiert beispielsweise bei a ⋅ a−1 = 1 und a ≠ 0.
Programmbedienung
Gehen Sie folgendermaßen vor, um eine schriftliche Multiplikation mit Hilfe dieses Moduls durchzuführen:
- Wählen Sie im Formularbereich Auswahl durch die Aktivierung des Kontrollschalters Zufällig bzw. Selbstdefiniert, ob eine Aufgabe durch den programminternen Zufallsgenerator erzeugt werden soll, oder ob Sie eine selbstdefinierte Aufgabe erstellen möchten.
- Wurde der Kontrollschalter Zufällig aktiviert, so legen Sie in den Formularbereichen 1. Faktor und 2. Faktor durch die Aktivierung des entsprechenden Kontrollschalters die Anzahl der Stellen der Zahlen fest, mit denen eine Berechnung durchgeführt werden soll.
Möchten Sie selbst eine eigene Aufgabe vorgeben, so aktivieren Sie hierfür zunächst den Kontrollschalter Selbstdefiniert, geben die entsprechenden Zahlenwerte in die dafür vorgesehenen Felder 1. Faktor und 2. Faktor ein und bedienen darauffolgend die Schaltfläche Zahlen übernehmen.
- Klicken Sie hierauf auf die entsprechenden Bedienschalter, die mit Zahlensymbolen versehen sind, um dem Programm das Ergebnis Ihrer Berechnung mitzuteilen. Wird ein korrekt ermittelter Zahlenwert eingegeben, so wird dieser im Ergebnisfeld ausgegeben. Wird hingegen eine falsche Taste bedient, so wird die Eingabe ignoriert.
Nach einer erfolgreich durchgeführten Schalter- bzw. Tastaturbedienung wird der zuletzt durchgeführte Rechenschritt angezeigt.
Eine neue Aufgabe kann erzeugt werden, indem der Schalter Neue Aufgabe, bzw. Zahlen übernehmen benutzt wird.
Möchten Sie die Aufgabe vom Programm lösen lassen, so bedienen Sie die Schaltfläche Lösung. Das Programm bearbeitet daraufhin alle zu durchlaufenden Rechenschritte und gibt das Ergebnis der Berechnung aus. Durch einen Klick auf die Schaltfläche Beenden schließen Sie dieses Unterprogramm.
Hinweis:
Zahlenwerte können auch durch die Benutzung der entsprechenden Tastaturtasten eingegeben werden.
Beispiel
Wurde der Kontrollschalter Selbstdefiniert aktiviert, wurden in die Felder 1. Faktor und 2. Faktor die Zahlen 331 und 16 eingetragen und der Schalter Zahlen übernehmen bedient, so gibt das Programm, nach einer aufeinanderfolgenden Bedienung der Schaltflächen (oder Eingabetasten der Tastatur) 1, 3, 3 und 6, 8, 9, 1 aus, dass die Aufgabe erfolgreich gelöst wurde, da eine Multiplikation der Zahlen 331 und 16 die Zahl 5296 ergibt.
Kommazahlen multiplizieren - Dezimalzahlen multiplizieren - Kommaschreibweise -Ausmultiplizieren - Faktorisieren - Ausklammern
Kommaschreibweise: Als Kommaschreibweise wird die Angabe von Zahlen (Messwerten) mit einem dafür vorgesehenen Einheitenvorsatz bezeichnet. Hierbei nimmt die Maßzahl einen Zahlenwert an, der mit einer entsprechenden Anzahl von Nachkommastellen versehen ist. Im Allgemeinen wird die Kommaschreibweise als die Darstellung von Zahlen in Dezimalschreibweise bezeichnet.
Ausmultiplizieren besagt, dass eine Summe, die sich innerhalb einer Klammer befindet, mit einem Faktor, der vor sich vor der Klammer befindet, ausmultipliziert wird. Hierbei werden sämtliche Summanden, die sich einzeln innerhalb der Klammer befinden, mit dem sich vor der Klammer befindendem Faktor multipliziert.
Beispiele (Ausmultiplizieren):
3 · (1 + 4) = 3 · 5 = 15
4 · (5 - 2) = 4 · 3 = 12
Das Faktorisieren (Ausklammern) besagt, dass eine Differenz oder eine Summe in ein Produkt gewandelt wird. Hierfür wird ein gemeinsamer Faktor festgelegt.
Beispiele (Ausklammer bzw. Faktorisieren):
3 · (1 + 4) = 3 · 1 + 3 · 4 = 3 + 12 = 15
4 · (5 - 2) = 4 · 5 - 4 · 2 = 20 - 8 = 12
Kommazahlen multiplizieren (Dezimalzahlen multiplizieren): Nachfolgend wird auf die Methoden eingegangen, die zur Durchführung der Multiplikation von Dezimalzahlen angewandt werden.
1. Multiplikation einer Dezimalzahl mit einer natürlichen Zahl:
Die Multiplikation einer Dezimalzahl mit einer natürlichen Zahl erfolgt, indem die Dezimalzahl in ihre Stellenwerte zerlegt und hierauf multipliziert wird. Danach werden die Teilergebnisse dieser durchgeführten Operationen addiert.
Beispiel:
Es sind die beiden Dezimalzahlen 1,69 und 7 miteinander zu multiplizieren.
Die Gesamtanzahl der Nachkommastellen beiden Zahlen werden gemerkt. Dies sind im vorliegenden Fall zwei.
Das Komma der ersten Zahl wird ignoriert und die beiden natürlichen Zahlen werden wie folgt miteinander multipliziert:
169 ⋅ 7 = 1183
Da insgesamt 2 Nachkommastellen vorhanden waren, ist das Komma im Ergebnis dieser Berechnung an die zweite Stelle von rechts zu setzen. Somit ergibt sich für die durchgeführte Multiplikation folgendes Resultat:
1,69 ⋅ 7 = 11,83
2. Multiplikation einer Dezimalzahl mit einer Dezimalzahl:
Zwei Dezimalzahlen werden miteinander multipliziert, indem zunächst die Kommata beider Zahlen ignoriert werden und die Multiplikation dieser durchgeführt wird. Hierauf werden die Nachkommastellen der beiden Faktoren gezählt und das Komma an der dafür relevanten Stelle im Ergebnis gesetzt.
Beispiel 1:
Es sind die beiden Dezimalzahlen 5,67 und 0,3 miteinander zu multiplizieren.
Die Gesamtanzahl der Nachkommastellen beiden Zahlen werden gemerkt. Dies sind im vorliegenden Fall drei.
Die Kommata dieser beiden Zahlen werden ignoriert und die beiden natürlichen Zahlen werden wie folgt miteinander multipliziert:
567 ⋅ 3 = 1701
Da insgesamt 3 Nachkommastellen vorhanden waren, ist das Komma im Ergebnis dieser Berechnung an die dritte Stelle von rechts zu setzen. Somit ergibt sich für die durchgeführte Multiplikation folgendes Resultat:
5,67 ⋅ 0,3 = 1,701
Beispiel 2:
Es sind die beiden Dezimalzahlen 306,2749 und 5,317 miteinander zu multiplizieren.
Die Gesamtanzahl der Nachkommastellen beiden Zahlen werden gemerkt. Dies sind im vorliegenden Fall sieben.
Die Kommata dieser beiden Zahlen werden ignoriert und die beiden natürlichen Zahlen werden wie folgt miteinander multipliziert:
3062749 ⋅ 5317 = 1628463543
Da insgesamt 7 Nachkommastellen vorhanden waren, ist das Komma im Ergebnis dieser Berechnung an die siebte Stelle von rechts zu setzen. Somit ergibt sich für die durchgeführte Multiplikation folgendes Resultat:
306,2749 ⋅ 5,317 = 1628,463543
Vielfache - Vielfaches
Vielfaches: Das Vielfache einer Zahl resultiert, wenn eine Zahl der Reihe nach mit einer festgelegten Anzahl natürlicher Zahlen multipliziert wird.
Verdoppelung: Unter dem Begriff Verdoppeln (oder Verdopplung) wird verstanden, eine Menge derart zu vergrößern, dass sie hierauf zweimal so groß ist.
Das Zweifache von: Das Zweifache (das Doppelte) einer Zahl a ist eine Zahl b, die resultiert, wenn die ursprüngliche Zahl zweimal (zwei Mal) aufeinanderfolgend mit sich selbst multipliziert wird. Für eine Zahl a gilt somit für deren Zweifaches (Doppeltes): b = a·a oder 2·a.
Das Dreifache von: Das Dreifache einer Zahl a ist eine Zahl b, die resultiert, wenn die ursprüngliche Zahl dreimal (drei Mal) aufeinanderfolgend mit sich selbst multipliziert wird. Für eine Zahl a gilt somit für deren Dreifaches: b = a·a·a oder 3·a.
Das Vierfache von: Das Vierfache einer Zahl a ist eine Zahl b, die resultiert, wenn die ursprüngliche Zahl viermal (vier Mal) aufeinanderfolgend mit sich selbst multipliziert wird. Für eine Zahl a gilt somit für deren Vierfaches: b = a·a·a·a oder 4·a.
Das Fünffache von: Das Fünffache einer Zahl a ist eine Zahl b, die resultiert, wenn die ursprüngliche Zahl fünfmal (fünf Mal) aufeinanderfolgend mit sich selbst multipliziert wird. Für eine Zahl a gilt somit für deren Fünffaches: b = a·a·a·a·a oder 5·a.
Das Sechsfache von: Das Sechsfache einer Zahl a ist eine Zahl b, die resultiert, wenn die ursprüngliche Zahl sechsmal (sechs Mal) aufeinanderfolgend mit sich selbst multipliziert wird. Für eine Zahl a gilt somit für deren Sechsfaches: b = a·a·a·a·a·a oder 6·a.
Das Siebenfache von: Das Siebenfache einer Zahl a ist eine Zahl b, die resultiert, wenn die ursprüngliche Zahl siebenmal (sieben Mal) aufeinanderfolgend mit sich selbst multipliziert wird. Für eine Zahl a gilt somit für deren Siebenfaches: b = a·a·a·a·a·a·a oder 7·a.
Das Achtfache von: Das Achtfache einer Zahl a ist eine Zahl b, die resultiert, wenn die ursprüngliche Zahl achtmal (acht Mal) aufeinanderfolgend mit sich selbst multipliziert wird. Für eine Zahl a gilt somit für deren Achtfaches: b = a·a·a·a·a·a·a·a oder 8·a.
Das Neunffache von: Das Neunfache einer Zahl a ist eine Zahl b, die resultiert, wenn die ursprüngliche Zahl neunmal (neun Mal) aufeinanderfolgend mit sich selbst multipliziert wird. Für eine Zahl a gilt somit für deren Neunfaches: b = a·a·a·a·a·a·a·a·a oder 9·a.
Das Zehnfache von: Das Zehnfache einer Zahl a ist eine Zahl b, die resultiert, wenn die ursprüngliche Zahl zehnmal (zehn Mal) aufeinanderfolgend mit sich selbst multipliziert wird. Für eine Zahl a gilt somit für deren Zehnfaches: b = a·a·a·a·a·a·a·a·a·a oder 10·a.
1er- Reihe - 2er-Reihe - 3er-Reihe - 4er-Reihe - 5er-Reihe - 6er-Reihe - 7er-Reihe - 8er-Reihe - 9er-Reihe - 10er-Reihe - Malfolgen - Malreihen
Das kleine Einmaleins (1×1 oder 1mal1 bzw. 1 mal 1) ist eine Aufstellung der Produkte, die aus der Kombination zweier natürlicher Zahlen von 1 bis 10 resultieren. Es zählt zum mathematischen Grundwisssen.
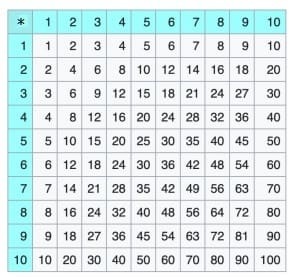
Mit Hilfe einer Multiplikationstabelle können alle Grundaufgaben der Multiplikation im Zahlenraum bis 100 mit den Multiplikatoren 1 bis 10 geübt werden.
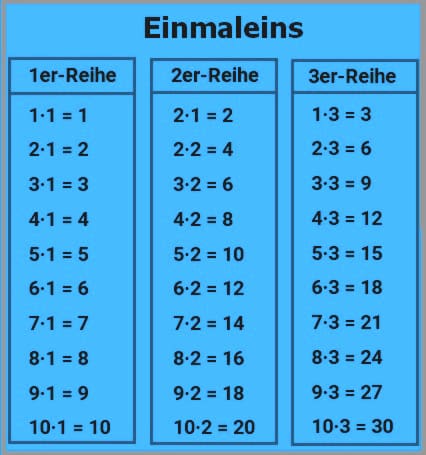
Einmaleinsreihen: Nachfolgend ist eine Zusammenstellung der einzelnen Kombinationen (Multipliaktionstabellen) aufgeführt. Sie gliedern sich in die folgenden Reihen (Einmaleinsreihen): 1er-Reihe (Einerreihe), 2er-Reihe (Zweierreihe), 3er-Reihe (Dreierreihe), 4er-Reihe (Viererreihe), 5er-Reihe (Fünferreihe), 6er-Reihe (Sechserreihe), 7er-Reihe (Siebenerreihe), 8er-Reihe (Achterreihe), 9er-Reihe (Neunerreihe) und 10er-Reihe (Zehnerreihe). Reihen dieser Art werden auch als Malreihen oder Malfolgen bezeichnet.
| 1er-Reihe | 2er-Reihe | 3er-Reihe | ||
| 1·1 = 1 | 2·1 = 2 | 1·3 = 3 | ||
| 2·1 = 2 | 2·2 = 4 | 2·3 = 6 | ||
| 3·1 = 3 | 3·2 = 6 | 3·3 = 9 | ||
| 4·1 = 4 | 4·2 = 8 | 4·3 = 12 | ||
| 5·1 = 5 | 5·2 = 10 | 5·3 = 15 | ||
| 6·1 = 6 | 6·2 = 12 | 6·3 = 18 | ||
| 7·1 = 7 | 7·2 = 14 | 7·3 = 21 | ||
| 8·1 = 8 | 8·2 = 16 | 8·3 = 24 | ||
| 9·1 = 9 | 9·2 = 18 | 9·3 = 27 | ||
| 10·1 = 10 | 10·2 = 20 | 10·3 = 30 |
| 4er-Reihe | 5er-Reihe | 6er-Reihe | ||
| 1·4 = 1 | 1·5 = 5 | 1·6 = 6 | ||
| 2·4 = 2 | 2·5 = 10 | 2·6 = 12 | ||
| 3·4 = 3 | 3·5 = 15 | 3·6 = 18 | ||
| 4·4 = 4 | 4·5 = 20 | 4·6 = 24 | ||
| 5·4 = 5 | 5·5 = 25 | 5·6 = 30 | ||
| 6·4 = 6 | 6·5 = 30 | 6·6 = 36 | ||
| 7·4 = 7 | 7·5 = 35 | 7·6 = 42 | ||
| 8·4 = 8 | 8·5 = 40 | 8·6 = 48 | ||
| 9·4 = 9 | 9·5 = 45 | 9·6 = 54 | ||
| 10·4 = 10 | 10·5 = 50 | 10·6 = 60 |
| 7er-Reihe | 8er-Reihe | 9er-Reihe | ||
| 1·7 = 7 | 1·8 = 8 | 1·9 = 9 | ||
| 2·7 = 14 | 2·8 = 16 | 2·9 = 18 | ||
| 3·7 = 21 | 3·8 = 24 | 3·9 = 27 | ||
| 4·7 = 28 | 4·8 = 32 | 4·9 = 36 | ||
| 5·7 = 35 | 5·8 = 40 | 5·9 = 45 | ||
| 6·7 = 42 | 6·8 = 48 | 6·9 = 54 | ||
| 7·7 = 49 | 7·8 = 56 | 7·9 = 63 | ||
| 8·7 = 56 | 8·8 = 64 | 8·9 = 72 | ||
| 9·7 = 63 | 9·8 = 72 | 9·9 = 81 | ||
| 10·7 = 70 | 10·8 = 80 | 10·9 = 90 |
| 10er-Reihe |
| 1·10 = 10 |
| 2·10 = 20 |
| 3·10 = 30 |
| 4·10 = 40 |
| 5·10 = 50 |
| 6·10 = 60 |
| 7·10 = 70 |
| 8·10 = 80 |
| 9·10 = 90 |
| 10·10 = 100 |
Die Einerreihe (1er-Reihe) ist die erste Reihe des kleinen Einmaleins. Sie beginnt mit der Zahl eins und endet mit der Zahl zehn. In der 1er Reihe werden alle natürlichen Zahlen von 1 bis 10 mit der Zahl 1 multipliziert.
Die Zweierreihe (2er-Reihe) ist die zweite Reihe des kleinen Einmaleins. Sie beginnt mit der Zahl zwei und endet mit der Zahl zwanzig. In der 2er Reihe werden alle natürlichen Zahlen von 1 bis 10 mit der Zahl 2 multipliziert.
Die Dreierreihe (3er-Reihe) ist die dritte Reihe des kleinen Einmaleins. Sie beginnt mit der Zahl drei und endet mit der Zahl dreißig. In der 3er Reihe werden alle natürlichen Zahlen von 1 bis 10 mit der Zahl 3 multipliziert.
Die Viererreihe (4er-Reihe) ist die vierte Reihe des kleinen Einmaleins. Sie beginnt mit der Zahl vier und endet mit der Zahl vierzig. In der 4er Reihe werden alle natürlichen Zahlen von 1 bis 10 mit der Zahl 4 multipliziert.
Die Fünferreihe (5er-Reihe) ist die fünfte Reihe des kleinen Einmaleins. Sie beginnt mit der Zahl fünf und endet mit der Zahl fünfzig. In der 5er Reihe werden alle natürlichen Zahlen von 1 bis 10 mit der Zahl 6 multipliziert.
Die Sechserreihe (6er-Reihe) ist die sechte Reihe des kleinen Einmaleins. Sie beginnt mit der Zahl sechs und endet mit der Zahl sechzig. In der 6er Reihe werden alle natürlichen Zahlen von 1 bis 10 mit der Zahl 6 multipliziert.
Die Siebenerreihe (7er-Reihe) ist die siebte Reihe des kleinen Einmaleins. Sie beginnt mit der Zahl sieben und endet mit der Zahl siebzig. In der 7er Reihe werden alle natürlichen Zahlen von 1 bis 10 mit der Zahl 7 multipliziert.
Die Achterreihe (8er-Reihe) ist die achte Reihe des kleinen Einmaleins. Sie beginnt mit der Zahl acht und endet mit der Zahl achtig. In der 8er Reihe werden alle natürlichen Zahlen von 1 bis 10 mit der Zahl 8 multipliziert.
Die Neunerreihe (9er-Reihe) ist die neunte Reihe des kleinen Einmaleins. Sie beginnt mit der Zahl neun und endet mit der Zahl neunzig. In der 9er Reihe werden alle natürlichen Zahlen von 1 bis 10 mit der Zahl 9 multipliziert.
Die Zehnerreihe (10er-Reihe) ist die zehnte Reihe des kleinen Einmaleins. Sie beginnt mit der Zahl zehn und endet mit der Zahl hundert. In der 10er Reihe werden alle natürlichen Zahlen von 1 bis 10 mit der Zahl 10 multipliziert.
Das große Einmaleins ist eine Aufstellung der Produkte, die aus der Kombination zweier natürlicher Zahlen von 1 bis 20 resultieren. Es ist die Erweiterung des kleinen Einmaleins auf natürliche Zahlen von 1 bis 20 und besitzt die gleiche Funktionsweise wie dieses.
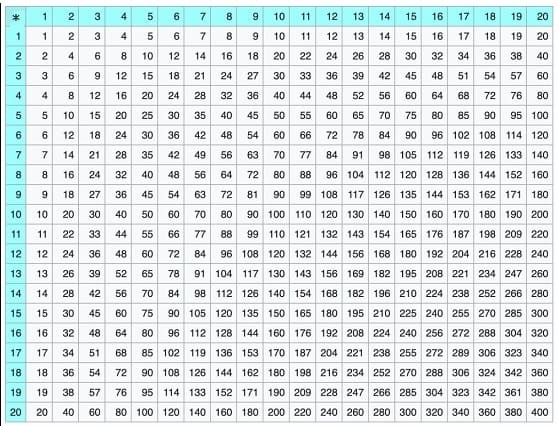
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben, wie Hausaufgaben zum behandelten Fachthema in Mathe. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu.Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet der Mathematik, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden.
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Weitere Themenbereiche

Beispiel 1

Beispiel 2

Beispiel 3

Beispiel 4
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Schriftliche Multiplikation sowie unter Wikipedia - Grundrechenarten zu finden.
Zahlenstrahl - Römische Zahlen - Schriftliche Addition - Schriftliche Subtraktion - Schriftliche Division - Schriftliche Potenzierung - Aussagenlogik - Zahltypumwandlung - Zinsrechnung - Zinseszinsrechnung grafisch - Annuitätentilgung - Jahreszinsrechnung - Physikalische Größen - Materialkonstanten - Fachbegriffe Deutsch - Englisch - Mandelbrot- und Juliamengen - Zusammenhänge Mandelbrot-Juliamengen - Sierpinski-Dreieck - Koch-Kurve - Pythagoras-Baum - Feigenbaum-Diagramm - Lindenmayer-System - Lindenmayer-System II - Logistische Gleichung I - Logistische Gleichung II - Diagramme - Tortendiagramm - Kryptografie - Raumgittermodelle (3D) - Paare geordnet - Kalender - Rechnen mit selbstdefinierten Formeln - Zeichenprogramm - Tangram - Tetris - Spiel 15 - Türme von Hanoi - Dame - Schach
MathProf 5.0 - Unterprogramm Schriftliche Division

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















