MathProf - Komplexe Zahlen - Schreibweisen - Umwandlung - Polar

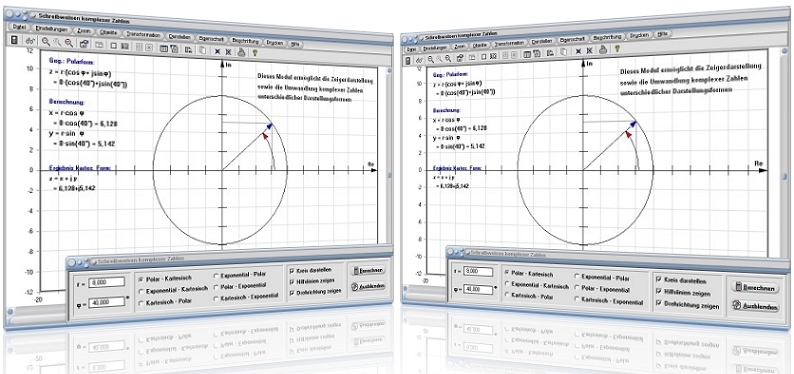
Modul Schreibweisen komplexer Zahlen

---

 
Das kleine Unterprogramm [Algebra] - [Komplexe Zahlen] - Schreibweisen komplexer Zahlen ermöglicht die Wandlung (Umrechnung) von Schreibweisen komplexer Zahlen in andere.

 

 

Da zur Darstellung komplexer Zahlen verschiedene Schreibweisen verwendet (benötigt) werden, ist oftmals deren Umwandlung in andere Formen notwendig. In diesem Programmmodul können die hierfür jeweils erforderlichen Berechnungsschritte nachvollzogen werden. Zudem wird die komplexe Zahl in der Gauß'schen Zahlenebene dargestellt. Zur Verfügung stehen folgende Möglichkeiten einer Umwandlung (Darstellungsformen):
 

• Polarform - Kartesische Form (Algebraische Form)
• Exponentielle Form - Kartesische Form (Algebraische Form)
• Kartesische Form (Algebraische Form) - Polarform
• Exponentielle Form - Polarform
• Polarform - Exponentielle Form
• Kartesische Form (Algebraische Form) - Exponentielle Form

  

 
Komplexe Zahlen können in folgenden Schreibweisen (Darstellungsformen) definiert werden:

1. Kartesische Form (algebraische Form):

z = x + jy

x: Realteil von z

y: Imaginärteil von z

j: Imaginäre Einheit (j² = -1)
 

2. Polarform:

z = r·(cos(φ) + j·sin(φ))

r: Betrag von z

φ: Argument (Winkel) von z
 

3. Exponentialform:

z = r·e^jφ

r: Betrag von z

φ: Argument (Winkel) von z

e: Eulersche Zahl

 
 

 
Gehen Sie folgendermaßen vor, die Umwandlung einer komplexen Zahl von einer Schreibweise in eine andere durchführen zu lassen:
 

1. Wählen Sie durch die Aktivierung des entsprechenden Kontrollschalters aus, welche der vorhandenen Schreibweisen Sie in eine andere wandeln möchten.
    
2. Geben Sie die Werte der zu wandelnden komplexen Zahl in die dafür vorgesehenen Felder ein.
    
3. Bedienen Sie die Schaltfläche Berechnen, so wird die schrittweise Wandlung der Zahl in die gewählte Form aufgezeigt.

 
Hinweis:

Bei Festlegung eines Winkelwerts ist dieser stets im Gradmaß anzugeben.

 
 

 

 

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:
 

• Kreis darstellen: Darstellung eines Kreises, der einen Radius vom Betrag der komplexen Zahl aufweist, ein-/ausschalten
• Hilfslinien zeigen: Darstellung der Hilfslinien, die den Real- bzw. Imaginärteil der Zahl beschreiben, ein-/ausschalten
• Drehrichtung zeigen: Pfeil, der die Drehrichtung des Zeigers beschreibt, ein-/ausschalten

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Einheitskreis komplexer Zahlen

Taschenrechner für komplexe Zahlen

Berechnungen mit komplexen Zahlen

Addition komplexer Zahlen

Multiplikation komplexer Zahlen

 

 
Beispiel 1 - Wandlung Polarform - Kartesische Form:

Nach einer Aktivierung des Kontrollschalters Polar - Kartesisch, einer Eingabe der Zahlenwerte 6 und 100 in die entsprechenden Felder sowie einer Bedienung der Schaltfläche Berechnen, werden folgende Schritte für die Wandlung der in Polarform gegebenen komplexen Zahl z = 6·(cos(100°) + j·sin(100°)) in die kartesische Form durchlaufen:

Polarform:

z = r·(cos(φ) + j·sin(φ))

  = r·(cos(100°) + j*sin(100°))
 

Berechnung:

x = r·cos(φ)

  = 6·cos(100°) = -1,042

     (nach Wandlung der Winkeleinheit in das Bogenmaß)

 

y = r·sin(φ)

  = 6·sin(100°) = 5,909

     (nach Wandlung der Winkeleinheit in das Bogenmaß)
 

Ergebnis (kartesische Form):

z = x + jy = -1,042 + j5,909

Beispiel 2 - Wandlung Exponentialform - Kartesische Form:

Wird der Kontrollschalters Exponential - Kartesisch aktiviert, werden die Zahlenwerte 4 und 60 in die entsprechenden Felder eingegeben und ein Klick auf die Schaltfläche Berechnen ausgeführt, so werden folgende Schritte für die Wandlung der in Exponentialform gegebenen komplexen Zahl z = 4·e^j60° in die kartesische Form durchlaufen:

Exponentialform:

z = r·e^jφ

  = 4·e^j60°
 

Wandlung in Polarform:

z = 4·(cos(φ) + j·sin(φ))

  = 4·(cos(60°) + j·sin(60°))
 

Berechnung (Wandlung der Polarform in Exponentialform):

x = r·cos(φ)

  = 4·cos(60°) = 2

     (nach Wandlung der Winkeleinheit in das Bogenmaß)

 

y = r·sin(φ)

  = 4·sin(60°) = 3,464

     (nach Wandlung der Winkeleinheit in das Bogenmaß)
 

Ergebnis (kartesische Form):

z = x + jy = 2 + j3,464

Bemerkung:

In diesem Fall ist die Durchführung eines zusätzlichen Berechnungsschritts erforderlich, da eine direkte Umwandlung von der Exponentialform in die Polarform nicht möglich ist.
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3

   

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
 

 

Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.

Wikipedia - Komplexe Zahl
Wikipedia - Imaginäre Zahl

Wikipedia - Darstellungsformen komplexer Zahlen
 

 

Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte

 

MathProf 5.0 - Unterprogramm Taschenrechner für komplexe Zahlen

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

  

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---