MathProf - Regression - Rechner - Nichtlineare Regression
Fachthema: Regression - Lineare Regression - Nichtlineare Regression - Rechner
MathProf - Statistik - Stochastik - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.
Online-Hilfe
für das Modul zur Durchführung von Analysen mit Hilfe
verschiedener Regressionsverfahren sowie dem Berechnen der entsprechenden Korrelationskoeffizienten (Regressionskoeffizienten) und resultierenden Regressionsfunktionen.
In diesem Tool wird die Anwendung der linearen Regression wie auch der nichtlinearen Regression ermöglicht.
Bei Durchführung der linearen Regressionsanalyse erfolgt hierbei unter anderem die Berechnung und Darstellung der relevanten Regressionsgerade (Ausgleichsgerade) unter Berücksichtigung der relevanten Irrtumswahrscheinlichkeit nach Festlegung relevanter Wertepaare bei Anwendung der Methode der kleinsten Quadrate.
Folgende Regressionsmodelle können zur Auswertung erfasster Daten angewandt werden:
Es wird ein Rechner für lineare Regression, logarithmische Regression, geometrische Regression, reziproke Regression, exponentielle Regression, trigonometrische Regression, reziproke quadratische Regression, kubische Regression bereitgestellt.
Dieses Unterprogramm beinhaltet zudem einige Beispiele zur Ermittlung
der Korrelation mit verschiedenen Modellen.
Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.
Themen und Stichworte zu diesem Modul:Regression - Regressionsmodelle - Analyse - Regressionsanalyse - Modell - Lineare Regression - Nichtlineare Regression - Nicht lineare Regression - Korrelationskoeffizient - Ausgleichskurve - Ausgleichspolynom - Regressionsrechnung - Lineares Regressionsmodell - Regressionsgleichung - Regressionsfunktion - Regressionskurve - Regressionsparameter - Ausgleichsgerade - Regressionsgerade - Regressionskoeffizient - Regressionsmodell - Linearer Zusammenhang - Korrelationsanalyse - Koeffizienten - Methode der kleinsten Quadrate - Methode der kleinsten Fehlerquadrate - Analysieren - Parameter - Konstante - Polynomiale Regression - Herleitung - Beweis - Grafik - Graph - Grafisch - Untersuchen - Untersuchung - Bilder - Wertepaare - Darstellung - Beispiel - Was ist - Was sind - Wieviel - Wie viel - Welche - Welcher - Welches - Wodurch - Bedeutung - Was bedeutet - Bestimmung - Bestimmen - Berechnen - Berechnung - Darstellen - Diagramm - Erklärung - Einfach erklärt - Beschreibung - Definition - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Grundlagen - Lernen - Erlernen - Begriff - Begriffe - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Mathe - Mathematik - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Einführung - Formel - Funktion - Abhängige Variable - Unabhängige Variable - Ursache - Wirkung - Wert - Rechner - Plotten - Plotter - Korrelation - Bivariate Korrelation - Logistische Regression - Scheinkorrelation - Korrelationsmaß - Korrelationsmaße - Zusammenhangsmaß - Zusammenhangsmaße - Standardisierte Regressionskoeffizienten - Standardisierter Regressionskoeffizient - Standardisierte Koeffizienten - Tabelle - Formeln - Zusammenhangsanalyse - Quadratische Regression - Logarithmische Regression - Reziproke Regression - Exponentielle Regression - Trigonometrische Regression - Kubische Regression |
Regression - Regressionsanalyse - Regressionsgerade - Regressionsfunktion
Modul Regressionsanalyse
Im Unterprogramm [Stochastik] - Regressionsanalyse können Regressionsanalysen mit verschiedenen Modellen durchgeführt werden. Hierbei erfolgt u.a. die Ermittlung des relevanten Korrelationskoeffizienten des entsprechenden Modells. Grafische Darstellungen sowie numerische Berechnungen erlauben das Interpretieren (die Interpretation) entsprechender Sachverhalte und Zusammenhänge zu diesem Fachthema.
Eine Regression beschreibt in der Statistik den Zusammenhang der zwischen zwei oder mehreren Variablen besteht. Mit dem Begriff Regressionsanalyse (Zusammenhangsanalyse) wird ein statistisches Analyseverfahren bezeichnet, welches unter Zuhilfenahme unterschiedlicher Modelle Zusammenhänge zwischen einer, oder mehreren unabhängigen Variablen hervorzubringen.
Der Begriff Regressionsrechnung ist ein anderer Ausdruck für den Fachbegriff Regressionsanalyse, die zur Beschreibung der funktionalen Abhängigkeit eines Merkmals durch ein oder mehrere andere Merkmale eingesetzt wird. Durch eine Anwendung von Regressionsanalysen können vermutete Zusammenhänge daraufhin überprüft werden, ob diese mit ermittelten Daten konsistent sind.
Regressionsmodelle sind Vorhersagemodelle. Ein Regressionsmodell bestimmt mit Hilfe einer mathematischen Funktion die Relation zwischen einer abhängigen und einer unabhängigen Variable.
Abhängige Variablen und unabhängige Variablen sind Variablen, die gemessen oder verändert werden, um Relationen zwischen Ursachen und Wirkungen in Fallstudien zu untersuchen. Als unabhängige Variable wird die Ursache bezeichnet. Deren Wert ist von anderen Variablen der Studie unabhängig. Die abhängige Variable ist die Wirkung. Sie hängt von Änderungen der unabhängigen Variable ab.
Dieses Modul ermöglicht die Durchführung von Untersuchungen mit folgenden Regressionsmodellen (lineare Regression und nichtlineare Regression):
- Lineare Regression Y = M·X+N (lineares Regressionsmodell)
- Logarithmische Regression Y = A+B·LN(X)
- Geometrische Regression Y = A·X^B
- Reziproke Regression Y = A+B/X
- Exponentielle Regression Y = A·B^X
- Trigonometrische Regression Y = A+B·SIN(X)
- Reziproke quadratische Regression Y = A+B/X²
- Quadratische Regression Y = A+B·X²
- Kubische Regression Y = A+B·X³
Hierbei werden nachfolgend aufgeführte Größen ermittelt und ausgegeben:
- Kleinster und größter Messwert (Minimum, Maximum)
- Mittelwert
- Median
- Varianz
- Standardabweichung (quadr. Streuung, durchschnittliche Abweichung der Messwerte vom Erwartungswert)
- Mittlerer Fehler des Mittelwerts
- Geometrisches Mittel
- Quadratisches Mittel
- Harmonisches Mittel
- Variationskoeffizient
- Stichprobenvarianz
- Stichproben-Standardabweichung
- Standardfehler
- Streubreite
- Mittlere Abweichung
- Mittelwert ohne größten Ausreißer (Max.)
- Mittelwert ohne kleinsten Ausreißer (Min.)
Als lineare Regression wird eine statistische Methode bezeichnet, die zur Ermittlung der Gleichung einer Gerade (linearen Funktion) dient, deren Koordinatenwerte näherungsweise einer Reihe zugrundeliegender Daten entsprechen.
Nicht lineare Regression (nichtlineare Regression): Als nichtlineare Regression wird eine statistische Methode bezeichnet, mit welcher ein nichtlinearer Zusammenhang (ein nicht lineares Modell) mit einer bestimmten Anzahl von Koordinatenwerten ermittelt werden kann.
Als quadratische Regression wird eine statistische Methode bezeichnet, die zur Ermittlung der Gleichung einer Parabel dient, deren Koordinatenwerte näherungsweise einer Reihe zugrundeliegender Daten entsprechen.
Als kubische Regression wird eine statistische Methode bezeichnet, die zur Ermittlung der Gleichung einer kubischen Parabel (kubischen Funktion) dient, deren Koordinatenwerte näherungsweise einer Reihe zugrundeliegender Daten entsprechen.
Als logarithmische Regression wird eine statistische Methode bezeichnet, die zur Ermittlung der Gleichung einer Logarithmusfunktion dient, deren Koordinatenwerte näherungsweise einer Reihe zugrundeliegender Daten entsprechen.
Als exponentielle Regression wird eine statistische Methode bezeichnet, die zur Ermittlung der Gleichung einer Exponentialfunktion dient, deren Koordinatenwerte näherungsweise einer Reihe zugrundeliegender Daten entsprechen.
Als trigonometrische Regression wird eine statistische Methode bezeichnet, die zur Ermittlung der Gleichung einer trigonometrischen Funktion dient, deren Koordinatenwerte näherungsweise einer Reihe zugrundeliegender Daten entsprechen.
Als polynomiale Regression wird eine statistische Methode bezeichnet, die zur Ermittlung der Gleichung eines Polynoms dient, dessen Koordinatenwerte näherungsweise einer Reihe zugrundeliegender Daten entsprechen. Im einfachsten Fall dieser Art wird hierdurch eine (quadratische) Parabel, ein Polynom 2. Grades, beschrieben. (Diese Art der Regression wird in diesem Modul nicht behandelt)
Logistische Regression: Mit Hilfe logistischer Regressionsmodelle wird die Abhängigkeit nominal abhängiger Variablen von anderen unabhängigen Variablen, die ein beliebiges Messniveau aufweisen, analysiert (z.B. die Anwesenheit bei einer Fortbildung j/n). Sie ist eine Art der Regressionsanalyse mit Hilfe derer ein nominalskaliertes, kategoriebezogenes Merkmal vorhersagbar gemacht wird. (Diese Art der Regression wird in diesem Modul nicht behandelt)
Zusätzlich ermittelte Größen - Formeln
Mittelwert:
Median:
falls n ungerade:
falls n gerade:
Varianz s²:
Standarabweichung:
Mittlerer Fehler des Mittelwerts:
Harmonisches Mittel:
Quadratisches Mittel:
Geometrisches Mittel:
Variationskoeffizient:
(Verhältnis der Standardabweichung zum arithmetischen Mittel)
Stichprobenvarianz:
Stichproben-Standardabweichung:
Standardfehler:
Mittlere Abweichung:
Mittelwert ohne Ausreißer (max):
Mittelwert
ohne größten (maximalen) Ausreißer
Mittelwert ohne Ausreißer (min):
Mittelwert
ohne kleinsten (minimalen) Ausreißer
1 - Lineare Regression
Lineare Regression: Die Methode der linearen Regression dient dem Zweck, eine möglichst gut an Messwerte angepasste, lineare Funktion zu ermitteln. Eine derartige Regressionsgleichung besitzt den Aufbau einer linearen Funktion und wird als Regressionsgerade oder Ausgleichsgerade bezeichnet.
Regressionskoeffizienten: Ein Regressionskoeffizient (auch als Regressionsparameter bezeichnet) bewertet den Einfluss einer Variablen in einer Regressionsgleichung. Koeffizienten dieser Art messen den Einfluss einer Variablen der in einer Regressionsgleichung vorkommt.
Bei einer Regressionsgleichung oder Regressionsfunktion handelt es sich um eine Gleichung bzw. Funktion, mit Hilfe derer die Prägnanz eines Merkmals aufgrund der Prägnanz eines anderen, mit dieser in Zusammenhang stehenden Merkmals prognostiziert werden kann.
Gesucht wird somit die Gleichung y = m·x+n einer Ausgleichsgeraden (Korrelationsgerade), von welcher gegebene Messwerte möglichst geringe Abstände aufweisen. Verwendet wird hierfür die Gaußsche Methode der kleinsten Quadrate (Methode der kleinsten Fehlerquadrate). Zugrundegelegt wird hierbei ein lineares Regressionsmodell.
Zusammenhangsmaß (Korrelationsmaß): Zusammenhangsmaße (Korrelationsmaße) dienen dazu, um zu analysieren in welcher Form (wie eng) zwei Größen miteinander in Verbindung stehen und zunehmen bzw. abnehmen. Hierzu zählt unter anderem der Korrelationskoeffizient. Um die Güte eines, auf diese Weise ermittelten, Zusammenhangs beurteilen zu können, wird der Korrelationskoeffizient ermittelt (-1 ≤ r ≤ 1, wobei r = 0 darauf hinweist, dass kein Zusammenhang zwischen den beiden Variablen x und y existiert).
Als Korrelationskoeffizient wird der Wert bezeichnet, der die Stärke einer linearen Beziehung zwischen zwei Variablen in einer Korrelationsanalyse bemisst.
Als Korrelationsanalyse wird ein statistisches Verfahren bezeichnet, welches Information über die zwischen Variablen bestehenden Relationen gibt.
Eine bivariate Korrelation bestimmt über einen Korrelationskoeffizienten die Stärke eines Zusammenhangs dessen zwischen zwei Merkmalen sowie seine Richtung (positiv oder negativ). Diese Methode findet in diesem Programm keine Anwendung.
Als Scheinkorrelation wird eine Korrelation bezeichnet die zwischen zwei Größen existiert, der jedoch kein kausaler Zusammenhang zugeordnet werden kann, sondern der lediglich eine zufällige oder indirekte Beziehung zugrunde liegt. Es kann kann nicht auf ein Ursache-Wirkungs-Prinzip zurückgeführt werden.
Standardisierter Regressionskoeffizient: Standardisierte Regressionskoeffizienten beschreiben in gleicher Form wie Korrelationskoeffizienten die Stärke eines Zusammenhangs und sind zwischen 0 und 1 normiert.
Bedienung dieses Unterprogramms
Das Programm ermittelt die zu dieser Beurteilung erforderlichen Werte und führt eine entsprechende Analyse durch. Es vergleicht anhand des eingestellten Konfidenzintervalls, ob mit der entsprechenden Wahrscheinlichkeit ein linearer Zusammenhang zwischen den x- und y-Werten besteht.
Wird beispielsweise eine Irrtumswahrscheinlichkeit von α = 0,1 gewählt und vom Programm ausgegeben, dass der "Zusammenhang wahrscheinlich" ist, so ist mit einer anzunehmenden Wahrscheinlichkeit von 99% davon auszugehen, dass ein linearer Zusammenhang zwischen den Messgrößen besteht.
Wird hingegen eine Irrtumswahrscheinlichkeit von α = 0,01 gewählt und vom Programm ermittelt, dass der Zusammenhang unwahrscheinlich ist, so muss die Annahme verworfen werden, dass mit 99,9%-iger Wahrscheinlichkeit ein linearer Zusammenhang zwischen den Messwerten vorliegt.
- Selektieren Sie den Eintrag Linear Y = M·X+N aus der aufklappbaren Box Auswahl Modell.
- Geben Sie die auszuwertenden Messdaten in die dafür vorgesehenen Felder X und Y ein, bedienen Sie die Schaltfläche Übernehmen und wiederholen Sie diesen Vorgang, bis alle erforderlichen Messwerte aufgenommen sind.
- Möchten Sie einen Eintrag in der Tabelle löschen, so fokussieren Sie diesen und bedienen die Schaltfläche Löschen. Soll ein bereits eingetragener Wert geändert werden, so fokussieren Sie zunächst den entsprechenden Eintrag in der Tabelle, geben den neuen Wert in das Eingabefeld ein und bedienen hierauf die Schaltfläche Ersetzen. Um alle Einträge zu löschen, kann die Schaltfläche Alle löschen verwendet werden.
- Wählen Sie durch die Selektion des entsprechenden Eintrags aus der Box Irrtumswahrsch. den Wert (0,1, 0,01, 0,05 bzw. 0,005) der zuzulassenden Irrtumswahrscheinlichkeit α.
- Bedienen Sie hierauf die Schaltfläche Berechnen.
- Möchten Sie sich die Verteilung der Messwerte, sowie den Verlauf der ermittelten Regressionsgeraden grafisch veranschaulichen, so klicken Sie hierauf auf die Schaltfläche Darstellen.
Hinweis:
2 - Nichtlineare Regression
Nichtlineare Regression: Die nichtlineare Regression stellt eine Form der Regressionsanalyse bereit, die eine nichtlineare Kombination der Modellparameter ist und von einer oder mehreren unabhängigen Variablen abhängig ist.
Als Ausgleichskurve (Regressionskurve) oder Ausgleichspolynom wird die mittels der Anwendung eines Regressionsmodells ermittelte Funktion und somit die Regressionsfunktion bezeichnet.
Bedienung dieses Unterprogramms
Da in der Praxis häufig die Analyse nichtlinearer Zusammenhänge erforderlich ist, ermöglicht das Programm auch die Durchführung einiger dieser. Hierbei werden die Parameter a und b der entsprechenden Funktion, sowie der zugehörige Korrelationskoeffizient, welcher Auskunft über die Qualität des Zusammenhangs der Messgrößen gibt, ermittelt. Es stehen zur Auswahl:
- Logarithmische Regression Y = A+B·LN(X)
- Geometrische Regression Y = A·X^B
- Reziproke Regression Y = A+B/X
- Exponentielle Regression Y = A·B^X
- Trigonometrische Regression Y = A+B·SIN(X)
- Reziproke quadratische Regression Y = A+B/X²
- Quadratische Regression Y = A+B·X²
- Kubische Regression Y = A+B·X³
Führen Sie Folgendes aus, um eine nichtlineare Regressionsanalyse mit Datenpaaren von Messwertreihen durchführen zu lassen:
- Wählen Sie den entsprechenden Eintrag aus der aufklappbaren Box Auswahl Modell.
- Geben Sie die auszuwertenden Messdaten in die dafür vorgesehenen Felder X und Y ein, bedienen Sie die Schaltfläche Übernehmen und wiederholen Sie diesen Vorgang, bis alle erforderlichen Messwerte aufgenommen sind.
- Möchten Sie einen Eintrag in der Tabelle löschen, so fokussieren Sie diesen und bedienen die Schaltfläche Löschen. Soll ein bereits eingetragener Wert geändert werden, so fokussieren Sie zunächst den entsprechenden Eintrag in der Tabelle, geben den neuen Wert in das Feld ein und bedienen hierauf die Schaltfläche Ersetzen. Um alle Einträge zu löschen, kann die Schaltfläche Alle löschen verwendet werden.
- Bedienen Sie die Schaltfläche Berechnen.
- Um sich die Verteilung der Messwerte, sowie den Verlauf der Kurve der ermittelten Regressionsfunktion grafisch zu veranschaulichen, klicken Sie hierauf auf die Schaltfläche Darstellen.
Hinweis:
| · Logarithmische Regression: | Alle X-Werte müssen > 0 sein |
| · Geometrische Regression: | Alle X-Werte und alle Y-Werte müssen > 0 sein |
| · Reziproke Regression: | Kein X-Wert darf 0 sein |
| · Reziproke quadr. Regression: | Kein X-Wert darf 0 sein |
| · Exponentielle Regression: | Alle Y-Werte müssen > 0 sein |
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Mathe-Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
- Punkte: Darstellung der Punktbeschriftung ein-/ausschalten
- Koordinaten: Darstellung der Koordinatenwerte der Punkte ein-/ausschalten
| X -Werte | Y-Werte |
| -15,722 | -1,274 |
| -13,852 | -0,456 |
| -6,968 | -0,288 |
| -3,484 | 0,793 |
| 0,4 | 1,658 |
| 1,0 | 1,0 |
| 2,33 | 1,899 |
| 14,872 | 2,596 |
| 19,971 | 1,0 |
| Anzahl der X-Werte: | 9 |
| Minimum: | -15,722 |
| Maximum: | 7 |
| Mittelwert: | -0,161444 |
| Median: | 0,4 |
| Varianz: | 140,765252 |
| Standardabweichung: | 11,864453 |
| Mittlerer Fehler des Mittelwerts: | 3,954818 |
| Geometrisches Mittel: | ----------- |
| Harmonisches Mittel: | 2,586087 |
| Quadratisches Mittel: | 11,187079 |
| Variationskoeffizient: | -871,911401 |
| Stichprobenvarianz: | 125,124668 |
| Stichproben-Standardabweichung: | 11,185914 |
| Standardfehler: | 1,318273 |
| Streubreite: | 19,571 |
| Mittlere Abweichung: | 8,75116 |
| Mittelwert ohne Ausreißer(max): | -2,678 |
| Mittelwert ohne Ausreißer(min): | -0,231625 |
| Anzahl der Y-Werte: | 9 |
| Minimum: | -1,274 |
| Maximum: | 2,596 |
| Mittelwert: | 0,769778 |
| Median: | 1 |
| Varianz: | 1,538021 |
| Standardabweichung: | 1,24017 |
| Mittlerer Fehler des Mittelwerts: | 0,41339 |
| Geometrisches Mittel: | ----------- |
| Harmonisches Mittel: | -5,375822 |
| Quadratisches Mittel: | 1,399888 |
| Variationskoeffizient: | 1,998006 |
| Stichprobenvarianz: | 1,36713 |
| Stichproben-Standardabweichung: | 1,169243 |
| Standardfehler: | 0,137797 |
| Streubreite: | 2,884 |
| Mittlere Abweichung: | 0,96163 |
| Mittelwert ohne Ausreißer(max): | 0,5415 |
| Mittelwert ohne Ausreißer(min): | 0,902 |
Beispiel 2 - Nichtlineare Regression (nichtlineares Regressionsmodell):
| X -Werte | Y-Werte |
| 1 | 1 |
| 4,2 | 3,6 |
| 7,6 | 4 |
| 10,2 | 4,2 |
| 12,9 | 4,7 |
| Anzahl der X-Werte: | 5 |
| Minimum: | 1 |
| Maximum: | 12,9 |
| Mittelwert: | 7,18 |
| Median: | 7,6 |
| Varianz: | 22,272 |
| Standardabweichung: | 4,719322 |
| Mittlerer Fehler des Mittelwerts: | 2,110545 |
| Geometrisches Mittel: | 5,304574 |
| Harmonisches Mittel: | 3,235758 |
| Quadratisches Mittel: | 8,328865 |
| Variationskoeffizient: | 3,10195 |
| Stichprobenvarianz: | 17,8176 |
| Stichproben-Standardabweichung: | 4,22109 |
| Standardfehler: | 0,943864 |
| Streubreite: | 11,9 |
| Mittlere Abweichung: | 3,664 |
| Mittelwert ohne Ausreißer(max): | 5,75 |
| Mittelwert ohne Ausreißer(min): | 8,725 |
| Anzahl der Y-Werte: | 5 |
| Minimum: | 1 |
| Maximum: | 4,7 |
| Mittelwert: | 3,5 |
| Median: | 4 |
| Varianz: | 2,11 |
| Standardabweichung: | 1,452584 |
| Mittlerer Fehler des Mittelwerts: | 0,649615 |
| Geometrisches Mittel: | 3,095579 |
| Harmonisches Mittel: | 2,52699 |
| Quadratisches Mittel: | 3,733363 |
| Variationskoeffizient: | 0,602857 |
| Stichprobenvarianz: | 1,688 |
| Stichproben-Standardabweichung: | 1,299231 |
| Standardfehler: | 0,290517 |
| Streubreite: | 3,7 |
| Mittlere Abweichung: | 1 |
| Mittelwert ohne Ausreißer(max): | 3,2 |
| Mittelwert ohne Ausreißer(min): | 4,125 |
Grafische Darstellung - Beispiel 1
Grafische Darstellung - Beispiel 2
Grafische Darstellung - Beispiel 3
Grafische Darstellung - Beispiel 4
Grafische Darstellung - Beispiel 5
Grafische Darstellung - Beispiel 6
Grafische Darstellung - Beispiel 7
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Regressionsanalyse zu finden.
Kombinatorik - Urnenmodell - Pfadregel - Galton-Brett - Statistische Messwertanalyse - Hypothesentest - Binomialverteilung - Binomialverteilung - Interaktiv - Binomialkoeffizienten - Geometrische Verteilung - Geometrische Verteilung - Interaktiv - Poisson-Verteilung - Poisson-Verteilung - Interaktiv - Hypergeometrische Verteilung - Hypergeometrische Verteilung - Interaktiv - Stetige Verteilungen - Glockenkurve - Stichproben - Stichproben - Verteilungen - Lottosimulation - Vierfeldertest - Bedingte Wahrscheinlichkeit - Zusammenhang von Messwerten - Experimente - Gesetz der großen Zahlen - Berechnung von Pi (Monte-Carlo-Methode)
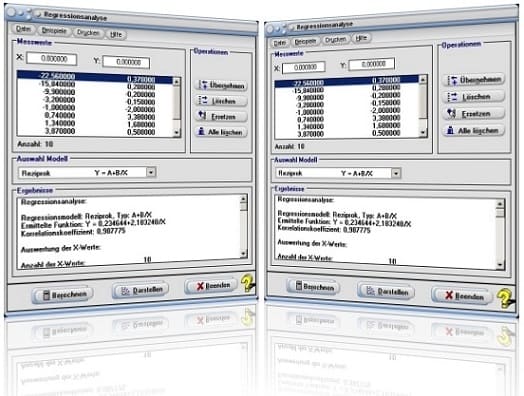
Startfenster des Unterprogramms Regressionsanalyse
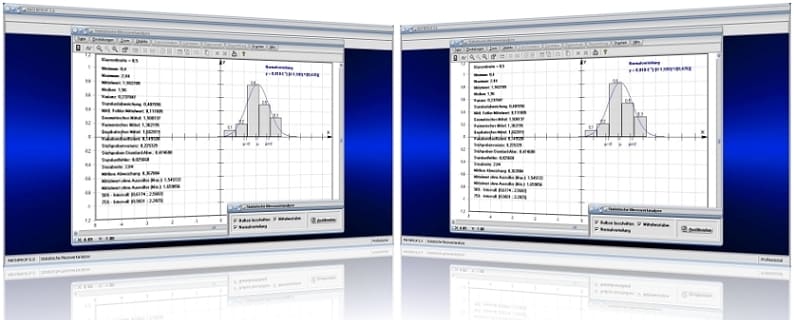
MathProf 5.0 - Unterprogramm Statistische Messwertanalyse
MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Physik interaktiv
Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
- Kurzinfos zum Themengebiet Mechanik
- Kurzinfos zum Themengebiet Elektrotechnik
- Kurzinfos zum Themengebiet Optik
- Kurzinfos zum Themengebiet Thermodynamik
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
