MathProf - Zentrische Streckung - Achsenspiegelung - Maßstab

Fachthemen: Zentrische Streckung - Scherung - Spiegelung - Drehung - Polygone - Maßstäbe - Zusammengesetzte Figuren
MathProf - Planimetrie - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Durchführung grundlegender affiner Transformationen bzw. Ähnlichkeitsabbildungen mit geometrischen Gebilden.
Dieses Teilprogramm ermöglicht unter anderem die Ausführung oben beschriebener Umwandlungen mit regelmäßigen Vielecken wie auch mit unregelmäßigen Vielecken.
Mit definierten Gebilden können Transformationen wie die Verschiebung bzw. Translation, die Parallelverschiebung, die Punktspiegelung, die Geradenspiegelung, die Achsenspiegelung, die zentrische Streckung bzw. Stauchung, die Drehung, die Drehstreckung sowie die Scherung ausgeführt werden. Auch lässt dieses Modul die Paktizierung der Verknüpfung (Hintereinanderausführung) von geometrischen Abbildungen dieser Art zu.
Zudem wird die Erzeugung und Berechnung von Kongruenzabbildungen von geometrischen Figuren bzw. geometrischen Flächen ermöglicht. Hierzu zählen Polygone wie das Dreieck, das Viereck, das Fünfeck, das Sechseck, das Achteck, das Zehneck und das Zwölfeck. Spiegelachsen, Spiegelgeraden, Spiegelpunkte und Hilfslinien können nach Bedarf eingeblendet oder ausgeblendet werden.
Symmetrie - Dieses Unterprogramm erlaubt auch die Durchführung von Untersuchungen mit geometrischen Figuren hinsichtlich derer Punktsymmetrie, derer Achsensymmetrie, derer Spiegelsymmetrie, derer Drehsymmetrie bzw. Rotationssymmetrie sowie weiterer geometrischer Eigenschaften.
Des Weiteren ermöglicht es das Berechnen der Punktkoordinaten der durch Spiegeln, Drehen, Verschieben oder Scheren transformierten Abbildungen. Der Rechner führt hierzu relevante Analysen durch, gibt die ermittelten Ergebnisse aus und stellt die entsprechenden Zusammenhänge grafisch dar.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben und dazu dienlich sind, Aufgaben zu diesem Themengebiet zu lösen, sind implementiert.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Zentrische Streckung - Geometrische Transformation - Punkte - Kongruenzabbildungen - Flächenschwerpunkt - Streckung - Verschiebung - Drehung - Drehstreckung - Gleitspiegelung - Schubspiegelung - Maßstab - Maßstäbe - Abbildungsmaßstab - Abbildungsmaßstäbe - Umrechnen - 1 zu 2 - 1 zu 50 - 1 zu 10 - 1 zu 100 - Vergrößern - Verkleinern - Vergrößerung - Verkleinerung - Maßstabsberechnung - Maßstabsumrechnung - Maßstabsleiste - Mehrfachspiegelung - Rotation - Streckfaktor - Streckzentrum - Streckungszentrum - Symmetriezentrum - Symmetrische Figuren - Symmetrie - Symmetrisch - Achsensymmetrie - Achsensymmetrisch - Punktsymmetrie - Punktsymmetrisch - Drehsymmetrie - Drehsymmetrisch - Achsensymmetrische Figuren - Punktsymmetrische Figuren - Drehsymmetrische Figuren - Deckungsgleich - Deckungsgleichheit - Koordinaten - Geometrische Figuren - Polygon - Geometrischer Begriff - Geometrischer Grundbegriff - Geometrische Begriffe - Geometrische Grundbegriffe - Geometrische Abbildungen - Zusammengesetzte Figuren - Zusammengesetzte Flächen - Zusammengesetzte Figur - Zusammengesetzte Fläche - Einfache Figur - Einfache Figuren - Begriff - Begriffe - Gesamtfläche - Teilfläche - Teilflächen - Eckenschwerpunkt - Ähnlichkeitsabbildung - Kongruente Figuren - Ähnliche Figuren - Ähnliche Dreiecke - Herleitung - Beweis - Spiegelfiguren - Drehzentrum - Drehen - Drehstrecken - Verschieben - Achsenspiegelung - Spiegelung an der x-Achse - Spiegelung an der y-Achse - Symmetrie - Skalierungsfaktor - X-Achse - Y-Achse - Ursprung - Abbildung - Bijektiv - Injektiv - Surjektiv - Surjektive Abbildung - Injektive Abbildung - Bijektive Abbildung - Vielecke - Halbdrehung - Vierteldrehung - Polygone - Eigenschaften - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Mathe - Mathematik - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Unregelmäßiges Vieleck - Unregelmäßiges Fünfeck - Dreieck spiegeln - Figuren spiegeln - Figuren drehen - Figuren verschieben - Figuren vergrößern - Figuren verkleinern - Figuren verschieben - Unmögliche Figuren - Unmögliche Figur - Hintereinanderausführung - Rotationszentrum - Drehzentrum - Drehpunkt - Spiegelpunkt - Spiegelgerade - Symmetrieachse - Symmetrieachsen - Doppelachsenspiegelung - Doppelspiegelung - Vergrößerung - Verkleinerung - Untersuchen - Untersuchung - Definition - Erklärung - Einfach erklärt - Beschreibung - Was ist - Bedeutung - Was bedeutet - Welche - Welcher - Welches - Wodurch - Ähnlichkeitsabbildungen - Zeichnen - Unregelmäßige Fläche - Fläche - Berechnung - Umfang - Bildpunkt verschieben - Bildpunkt spiegeln - Graph - Figur - Grafisch - Plotten - Bild - Plotter - Punkte - Bildpunkte - Präsentation - Grafik - Dreieck - Viereck - Fünfeck - Sechseck - Achteck - Flächeninhalt - Gerade - Hilfsline - Zeichnen - Verändern - Veränderung - Ändern - Änderung - Faktor - Zentrum - Winkel - Ecken - Fläche - Abbilden - Abbildung - Bildfigur - Originalfigur - Tabelle - Rechner - Beispiel - Berechnen - Formel - Gaußsche Trapezformel - Dreiecksformel - Spiegelsymmetrie - Verkleinerungsmaßstab - Vergrößerungsmaßstab - Maßstäbliches Vergrößern - Maßstäbliches Verkleinern - Figuren vergrößern - Figuren verkleinern - Kongruenzabbildung - Abbildungsmatrizen - Abbildungsmatrix - Längentreu - Längentreue Abbildung - Längentreue - Ähnlichkeit - Ähnlichkeiten - Ähnlichkeitsfaktor |
Polygone - Vielecke - Figuren - Maßstäbe

Modul Polygone
Das Unterprogramm [Geometrie] - Polygone ermöglicht es, Polygone (Vielecke) einer Auswahl grundlegender geometrischer Transformationen zu unterziehen.

Dieses Modul erlaubt die Erzeugung von Polygonen (Figuren), die durch bis zu 12 Eckpunkte beschrieben werden und die Nacheinanderausführung von bis zu vier geometrischen Operationen mit diesen. Es ermöglicht die Erstellung von Ähnlichkeitsabbildungen (Kongruenzabbildungen).
Zur Durchführung geometrischer (affiner) Transformationen stehen zur Auswahl:
-
Verschiebung - Translation (Verschieben)
Verschiebung eines Objekts, beschrieben durch die Punkte P1-Pn, in x- wie in y- Achsrichtung, um festgelegte Werte für dx und dy. -
Punktspiegelung (Punktspiegeln)
Punktspiegelung eines Objekts, beschrieben durch die Punkte P1-Pn, an einem Spiegelpunkt SP. -
Geradenspiegelung (An Gerade spiegeln - Achsenspiegelung - Spiegelachse)
Geradenspiegelung eines Objekts, beschrieben durch die Punkte P1-Pn, an einer Gerade durch die Punkte GP1 und GP2. -
Streckung / Stauchung (Strecken und Stauchen mit Streckfaktor)
Zentrische Streckung eines Objekts, beschrieben durch die Punkte P1-Pn, mit Streckzentrum S und Streckung mit festlegbarem Streckfaktor. -
Drehung - Rotation (Drehen)
Drehung eines Objekts, beschrieben durch die Punkte P1-Pn, um Drehpunkt D um festlegbaren Drehwinkel. -
Drehstreckung (Drehstrecken - Drehen und Strecken mit Streckfaktor)
Drehung eines Objekts, beschrieben durch die Punkte P1-Pn, um Drehpunkt DS um festlegbaren Drehwinkel und anschließender Streckung mit festlegbarem Streckfaktor. -
Scherung an x-Achse (Scheren an x-Achse)
Scherung eines Objekts, beschrieben durch die Punkte P1-Pn, an der x-Achse mit festlegbarem Scherfaktor. -
Scherung an y-Achse (Scheren an y-Achse)
Scherung eines Objekts, beschrieben durch die Punkte P1-Pn, an der y-Achse mit festlegbarem Scherfaktor. -
Scherung an einer Geraden (An Gerade scheren)
Scherung eines Objekts, beschrieben durch die Punkte P1-Pn, an einer Geraden durch die Punkte GP1-GP2 mit festlegbarem Scherwinkel. -
Affine Transformation
Affine Transformation eines Objekts, beschrieben durch die Punkte P1-Pn, unter Verwendung der Matrix, deren Koeffizienten a und b festlegbar sind:

Polygone - Vielecke
Polygone sind geschlossene ebene Figuren, deren Seiten aus geradlinigen Begrenzungsstrecken bestehen. Es sind Vielecke, welche durch ihre Anzahl an Ecken bestimmt sind. Von einem regelmäßigen Polygon wird gesprochen, wenn all seine Seiten gleich lang und alle Innenwinkel gleich groß sind und es keine überschneidenden Seiten besitzt. Polygone dieser Art sind bespielsweise ein gleichseitiges Dreieck, ein Quadrat, ein Pentagon, ein Hexagon, ein Heptagon oder ein Oktagon.
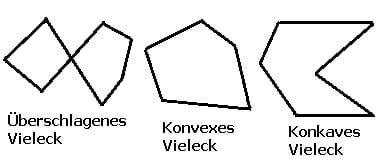
Ein Vieleck dessen Seiten sich überschneiden wird als überschlagenes Vieleck bezeichnet.
Ein Vieleck, bei welchem jede Verbindungsstrecke im Inneren des Polygons verläuft, wird als konvexes Vieleck bezeichnet.
Ein Vieleck, bei welchem mindestens ein Innenwinkel größer als 180° ist, wird als konkaves Vieleck bezeichnet.
Geometrische Transformationen
Nachfolgend sind Erläuterungen zu grundlegenden geometrischen Transformationen zu finden.
Zentrische Streckung:
Eine zentrische Streckung ist eine Bewegung, die alle Strecken in einem bestimmten, gegebenen Verhältnis vergrößert oder verkleinert. Sie ist durch ihr Zentrum sowie einen von ihr verschiedenen Punkt eindeutig festgelegt. Alle Bildstrecken verlaufen parallel zu den jeweils ursprünglichen Strecken.
Streckung:
Eine Streckung ist eine Bewegung, bei welcher alle Winkel unverändert bleiben und sich die Längenverhältnisse der Bildstrecken um einen festen Faktor vergrößern (Proportionalitätsfaktor > 1).
Stauchung:
Eine Stauchung ist eine Bewegung, bei welcher alle Winkel unverändert bleiben und sich die Längenverhältnisse der Bildstrecken um einen festen Faktor verkleinern (Proportionalitätsfaktor < 1).
Verschiebung:
Eine Verschiebung (Parallelverschiebung, Translation) ist eine Bewegung, bei welcher jeder Punkt der Bildebene, oder des Raums in dieselbe Richtung sowie um dieselbe Strecke verschoben wird.
Punktspiegelung:
Eine Punktspiegelung in der Ebene um einen Punkt P entspricht der Drehung um 180° bezüglich eines Drehzentrums P. Der Punkt P, an dem gespiegelt wird entspricht dem Schnittpunkt der Drehachse und der Spiegelebene. Er wird als Symmetriezentrum bezeichnet. Punktspiegelungen sind sowohl winkel-, längen- wie auch geradentreu.
Geradenspiegelung:
Eine Geradenspiegelung ordnet jedem Punkt P einen Bildpunkt P' zu, welcher dadurch bestimmt ist, dass die Verbindungsstrecke [PP'] von der Gerade rechtwinklig halbiert wird.
Drehung (Rotation):
Eine Drehung um einen Punkt P in der Ebene mit einem Drehwinkel α ist eine eineindeutige Abbildung auf sich selbst. Jede Drehung verfügt über einen Fixpunkt, welcher auf sich selbst abgebildet wird. Die Ausführung einer Drehung um einen Winkel von 360° entspricht der identischen Abbildung.
Achsenspiegelung: Als Achsenspiegelung wird eine geometrische Transformation bezeichnet, bei der ein Punkt, oder eine geometrische Figur an einer Achse bzw. Geraden, gespiegelt wird. Figuren, die hierdurch entstehen, werden als achsensymmetrisch bezeichnet.
Drehstreckung:
Eine Drehstreckung ist eine Ähnlichkeitsabbildung, welche sich in Form einer Kombination der beiden geometrischen Operationen Drehung und Streckung darstellen lässt.
Scherung:
Eine Scherung ist eine affine Abbildung auf sich selbst, bei welcher in der Ebene der Flächeninhalt der geometrischen Abbildung erhalten bleibt. Jeder Punkt der Achse der Geraden (Scherungsachse) an welcher die Scherung ausgeführt wird, wird auf sich abgebildet (bleibt fix). Der Abstand jedes Punktes zur Achse der Geraden bleibt unverändert.
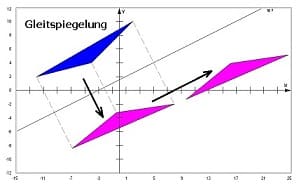
Gleitspiegelung (Schubspiegelung):
Unter einer Gleitspiegelung (Schubspiegelung) wird eine Spiegelung an einer Geraden (Spiegelachse) verstanden, bei der die Translation parallel zur Geraden vonstatten geht.
Geometrische Begriffe - Geometrische Grundbegriffe
Achsensymmetrie - Punktsymmetrie - Drehsymmetrie - Kongruenz - Flächeninhalt - Längentreue - Deckungsgleichheit
Nachfolgend sind einige geometrische Begriffe (geometrische Grundbegriffe) hinsichtlich der Symmetrie von Figuren sowie zu Kongruenzabbildungen erläutert.
1. Achsensymmetrie:
Eine geometrische Figur wird als achsensymmetrisch bezeichnet, wenn sie durch vertikale Achsenspiegelung an ihrer Symmetrieachse auf sich selbst abgebildet werden kann. Im zweidimensionalen Bereich entspricht die Achsensymmetrie der Spiegelsymmetrie. Eine Figur wird als achsensymmetrisch (spiegelsymmetrisch) bezeichnet, wenn sie durch eine Achsenspiegelung an einer ihrer Symmetrieachsen auf sich selbst abgebildet wird. Figuren dieser Art tragen die Bezeichnung achsensymmetrische Figuren.
Beispiele für achsensymmetrische Figuren:
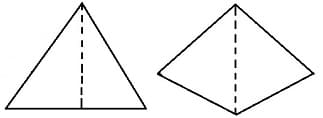
2. Punktsymmetrie:
Eine geometrische Figur wird als punktsymmetrisch bezeichnet, wenn sie im Zweidimensonalen um einen Punkt um 180° gedreht werden kann ohne dabei ihr Aussehen zu verändern. Die Bezeichnung dieses Punktes lautet Spiegelpunkt oder Spiegelzentrum bzw. Symmetriezentrum. Figuren dieser Art tragen die Bezeichnung punktsymmetrische Figuren.
Beispiele für punktsymmetrische Figuren:
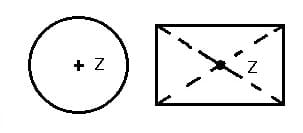
3. Drehsymmetrie:
Eine geometrische Figur wird als drehsymmetrisch bezeichnet, wenn sie nach Ausführung einer Drehung unverändert bleibt, bzw. auf sich selbst abgebildet wird. Figuren dieser Art werden als drehsymmetrische Figuren bezeichnet.
4. Kongruenz - Kongruenzabbildungen:
Zwei Figuren sind kongruent, wenn sie durch eine Kongruenzabbildung ineinander überführt werden können. Als kongruente Figuren werden geometrische Figuren bezeichnet, die in Form und Größe übereinstimmen.
Unter den vier Kongruenzabbildungen werden Lageänderungen von Figuren verstanden, bei welchen sich nach deren Ausführung weder deren Form noch Größe von den Originalen unterschieden. Zu ihnen zählen die Punktspiegelung, die Geradenspiegelung, die Verschiebung sowie die Drehung.
Abbildungsmatrizen für Kongruenzabbildungen:
1. Abbildungsmatrix für Punktspiegelung:

2. Abbildungsmatrix für Geradenspiegelung:

3. Abbildungsmatrix für Drehung an Ursprungsgerade:

5. Ähnlichkeitsabbidungen (Ähnlichkeiten):
Unter einer Ähnlichkeitsabbidung (Ähnlichkeit) wird in der Geometrie eine Affinität bezeichnet, welche Streckenverhältnisse und Winkelgrößen unverändert lässt, jedoch die Längen von Strecken ändert. Entsprechende Seiten sind unterschiedlich lang, besitzen jedoch dasselbe Längenverhältnis. Zu diesen zählen die zentrische Streckung, die Parallelstreckung sowie die Scherung.
Abbildungsmatrizen für Ähnlichkeitsabbidungen:
a. Abbildungsmatrix für zentrische Streckung:

b. Abbildungsmatrix für Dehnung bzw. Stauchung:

c. Abbildungsmatrix für Scherung an x-Achse:

Ähnliche Figuren: Ähnliche Figuren besitzen die gleiche Form, unterscheiden sich jedoch in ihrer Größe und Position.
Ähnliche Dreiecke: Ähnliche Dreiecke besitzen die gleiche Form, unterscheiden sich jedoch in ihrer Größe und Position.
6. Fächeninhalt:
Der Flächeninhalt eines konvexen Polygons kann ermittelt werden, indem alle von einem beliebigen Eckpunkt dessen ausgehenden Diagonalen eingezeichnet werden, das Polygon somit im Gegenuhrzeigersinn in n-2 Dreiecke zerlegt wird und die Summe der Flächen dieser gebildet wird.
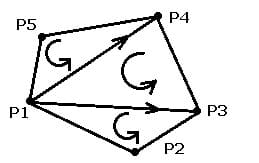
Der Flächeninhalt eines konvexen Polygons beträgt somit:
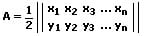
bzw. unter Anwendung der Gaußschen Trapezformel (Dreiecksformel) gilt:
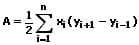
Diese Formel trägt die Bezeichnung Gaußsche Trapezformel.
7. Längentreue Abbildung:
Als Längentreue wird eine Eigenschaft geometrischer Abbildungen bezeichnet. Eine deratige Abbildung heißt längentreu, wenn der Abstand zweier ihrer Punkte A und B stets mit dem Abstand der zugehörigen Bildpunkte A' und B' übereinstimmt. Als Beispiele für längentreue Abbildungen seien Achsenspiegelungen, Punktspiegelungen, Verschiebungen sowie Drehungen genannt. Längentreue spielt insbesondere in der Kartografie (Kartenprojektion) eine wesentliche Rolle.
8. Deckungsgleichheit:
Als deckungsgleich werden Figuren bezeichnet, die in einer Form übereinander liegen, dass die oberhalb positionierte Figur die darunterliegende vollständig bedeckt.
Sonstige Fachbegriffe
Geometrische Transformation: Als geometrische Transformationen werden Abbildungen von einer in eine andere Punktmenge bezeichnet.
Kongruenzabbildungen: Als Kongruenzabbildung oder Ähnlichkeitsabbildung wird die umkehrbar eindeutige Abbildung einer Figur auf eine andere Figur bezeichnet. Sie ist eine umkehrbar eindeutige Abbildung einer Figur F1 auf eine andere Figur F2, bei der Form und Größe der abgebildeten Objekte erhalten bleiben. Es handelt sich um geometrische Abbildung bei der Form und Größe der abgebildeten Objekte erhalten bleiben.
Vergrößern (Vergrößerung): Das Vergrößern heißt, eine Figur in ihrer Ausdehnung, ihrem Umfang größer zu machen.
Verkleinern (Verkleinerung): Das Verkleinern heißt, eine Figur in ihrer Ausdehnung, ihrem Umfang kleiner zu machen.
Streckfaktor: Der Streckfaktor k gibt die Dimension einer Vergrößerung oder Verkleinerung an. Er ist der Quotient aus der Bildstreckenlänge und der Länge der Ausgangsstrecke. Beispiel: |k| = BA' : BA.
Streckzentrum (Streckungszentrum): Als Streckzentrum Z wird der Bezugspunkt einer zentrischen Streckung bezeichnet. Alle Strecken, die von diesem Zentrum zu jedem Punkt einer zu streckenden Figur verlaufen, werden um den Streckfaktor k vergrößert.
Symmetriezentrum (Punktsymmetrie, punktsymmetrisch): Kann eine geometrische Figur an einem Punkt derartig gespiegelt werden, dass sie hierdurch auf sich selbst abgebildet wird, so ist sie punktsymmetrisch. Der Punkt an dem die Spiegelung stattfindet, wird als Symmetriezentrum bezeichnet.
Spiegelfiguren: Als Spiegelfiguren werden Figuren bezeichnet, die durch Spiegelung an einem Punkt oder einer Gerade entstanden sind.
Drehzentrum: Als Drehzentrum wird der Punkt bezeichnet, um den ein geometrisches Objekt gedreht wird. Dieser kann sich innerhalb oder außerhalb der zu drehenden Figur befinden.
Symmetrische Figuren: Zwei (oder mehrere) verschiedene geometrische Objekte werden als symmetrische Figuren bezeichnet, wenn sie, gemeinsam betrachtet, eine symmetrische Figur bilden.
Geometrische Abbildungen: Als geometrische Abbildung wird eine Abbildung oder Funktion zwischen Räumen bezeichnet, die geometrisch definiert ist oder geometrisch gedeutet werden kann.
Unregelmäßiges Vieleck: Als unregelmäßiges Vieleck wird ein Vieleck bezeichnet, welches unterschiedlich lange Außenseiten und somit verschieden große Innenwinkel besitzt.
Unregelmäßiges Viereck: Als unregelmäßiges Viereck wird ein Viereck bezeichnet, welches unterschiedlich lange Außenseiten und somit verschieden große Innenwinkel besitzt.
Unregelmäßiges Fünfeck: Als unregelmäßiges Fünfeck wird ein Fünfeck bezeichnet, welches unterschiedlich lange Außenseiten und somit verschieden große Innenwinkel besitzt.
Unregelmäßiges Sechseck: Als unregelmäßiges Sechseck wird ein Sechseck bezeichnet, welches unterschiedlich lange Außenseiten und somit verschieden große Innenwinkel besitzt.
Flächenschwerpunkt: Als Flächenschwerpunkt wird der geometrische Schwerpunkt von Flächen bezeichnet.
Mehrfachspiegelung: Das Hintereinanderausführen mehrer Spiegelungen wird Mehrfachspiegelung genannt.
Spiegelgerade: Als Spiegelgerade wird die Gerade bezeichnet, an der die Spiegelung an einer Geraden vollzogen wird.
Spiegelachse (Symmetrieachse): Eine Spiegelachse oder Symmetrieachse halbiert eine Figur. Sie zerlegt eine Figur in zwei deckungsgleiche (kongruente) und gleich große Teile.
Doppelachsenspiegelung (Doppelspiegelung): Als Doppelachsenspiegelung oder Doppelspiegelung wird ein zweimaliges Spiegeln an zwei Geraden, die zueinander senkrecht stehen, bezeichnet.
Flächeninhalt: Der Flächeninhalt ist das Maß für die Größe der Fläche eines zweidimensionalen Gebildes.
Teilflächen: Als Teilfläche wird eine regelmäßige Fläche bezeichnet, die Teil einer allgemeinen Fläche ist. Zur Berechnung einer allgemeinen Fläche wird diese in regelmäßige Teilflächen zerlegt.
Bildfigur und Originalfigur: Als Originalfigur wird im vorliegenden Zusammenhang das Gebilde bezeichnet, mit welchem eine Transformation durchgeführt wird. Die Bildfigur ist das durch diese ausgeführte Transformation entstehende Abbild dieser Originalfigur.
Unmögliche Figuren: Eine unmögliche Figur ist ein zweidimensionales grafische Gebilde welches vorgetäuscht ein dreidimensionales Konstrukt darstellt, welches in Form eines Körpers nicht existieren kann. Hierbei handelt es sich um optische Täuschungen oder Widersinniges.

Abbildungen in der Ebene
Eine Abbildung ist definiert, wenn eine Vorschrift A jedem Originalelement einer Menge M exakt ein Bildelement einer Menge M' zuordnet.
Surjektive Abbildung: Vorschrift A wird als surjektiv bezeichnet, wenn jedes Element von M' in Form eines Bildes auftritt.
Injektive Abbildung: Vorschrift A wird als injektiv bezeichnet, wenn jedes Bildelement exakt ein Originalelement besitzt.
Bijektive Abbildung: Vorschrift A wird als bijektiv bezeichnet, wenn Vorschrift A sowohl surjektiv als auch injektiv ist.
Zusammengesetzte Figuren - Zusammengesetzte Flächen - Flächeninhalt - Berechnen
Zusammengesetzte Figuren - Zusammengesetzte Flächen: Als zusammengesetzte Figur oder zusammengesetzte Fläche wird eine geometrische Figur bezeichnet, die sich in mehrere einfache Figuren zerlegen lässt. Der Flächeninhalt zusammengesetzter Figuren wird berechnet, indem der Flächeninhalt jeder einzelner dieser Figuren berechnet wird und die Flächeninhalte dieser Gebilde (Teilflächen) hierauf addiert werden.
Beispiel 1:
Das nachfolgend gezeigte Beispiel illustriert eine zu praktizierende Vorgehensweise zur Berechnung des Flächeninhalts einer zusammengesetzten Figur.
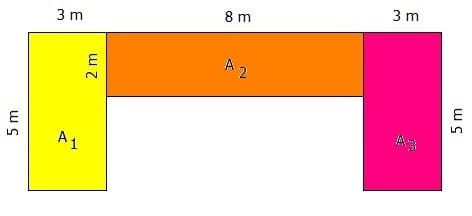
Dieses Gebilde setzt sich aus drei einzelnen Figuren (Rechtecken) zusammen. Somit sind zunächst die jeweiligen Flächeninhalte A1, A2 und A3 dieser Gebilde zu ermitteln und diese anschließend aufzusummieren.
Der Flächeninhalt des gelben Rechtecks A1 = a · b beträgt 5 m · 3 m = 15 m².
Der Flächeninhalt des orangefarbig markierten Rechtecks A2 = c · d beträgt 8 m · 2 m = 16 m².
Der Flächeninhalt des roten Rechtecks A3 = e · f beträgt ebenfalls 5 m · 3 m = 15 m².
Somit beträgt des gesamte Flächeninhalt (die Gesamtfläche) dieses dargestellten Gebildes: AGes = A1 + A2 + A3 = 15 m² + 16 m² + 15 m² = 46 m².
Die Ermittlung des gesamten Umfangs des dargestellten Gebildes kann wie folgt durchgeführt werden.
Der Umfang des gelben Rechtecks U1 = a + b beträgt 5 m + 3 m = 8 m.
Der Umfang des orangefarbig markierten Rechtecks U2 = c + d beträgt 8 m + 2 m = 10 m.
Der Umfang des roten Rechtecks U3 = e + f beträgt ebenfalls 5 m + 3 m = 8 m.
Hieraus ergibt sich für den gesamten Umfang der dargestellten Figur: Uges = U1 + U2 + U3 = 8m + 10m + 8 m = 26 m.
Beispiel 2:
Eine weitere Möglichkeit den gesamten Flächeninhalt dieser drei Rechtecke zu bestimmen sei im Folgenden gezeigt.
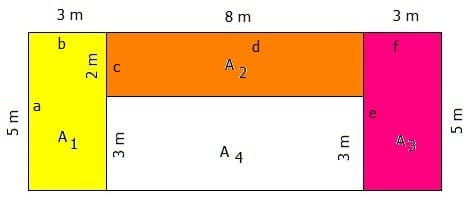
In diesem Fall wird zunächst der Flächeninhalt des umrahmenden Rechtecks ermittelt und hierauf wird von diesem der Flächeninhalt des weißen Rechtecks subtrahiert.
Der Flächeninhalt des umrahmenden Rechtecks beträgt: Ages = 5 m · (3 m + 8 m + 3 m) = 5 m · 14 m = 70 m² .
Hierauf wird die Fläche des weißen Rechecks ermittelt. Diese beträgt: A4 = 3 m · 8 m = 24 m²
Der Flächeninhalt der drei farbig markierten Rechtecke beträgt somit: Ages - A4 = 70 m² - 24 m² = 46 m².
Maßstab - Maßstäbe - Vergrößerung - Verkleinerung - Abbildungsmaßstab - Skalierungsfaktor
Ein Maßstab (Abbildungsmaßstab oder Skalierungsfaktor) beschreibt die Relation eines Originals in Bezug auf seine Abbildung. Er wird durch das Verhältnis zweier Zahlen ausgedrückt. Die erste Zahl bezieht sich auf die Größe der Abbildung, die zweite auf die Größe des Originals. Seine Darstellung erfolgt in nachfolgend gezeigten Formen:
1 : x Abbildung ist um den Faktor x kleiner als das Original (Verkleinerungsmaßstab)
x : 1 Abbildung ist um den Faktor x größer als das Original (Vergrößerungsmaßstab)
Das enstprechende Verhältnis wird als Ähnlichkeitsfaktor bezeichnet.
Maßstäbe (Abbildungsmaßstäbe) finden unter anderem Anwendung bei Grafiken, Zeichnungen oder geografischen Karten.
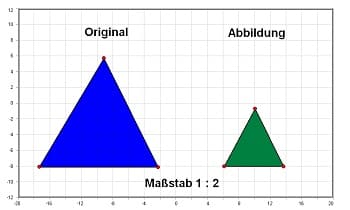
Beispiel - Bild 1: Verkleinerung: Maßstab 1 : 2 (Verkeinerungssmaßstab)
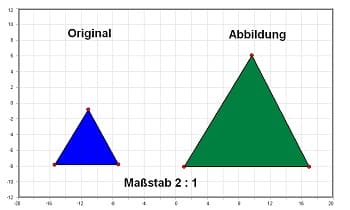
Beispiel - Bild 2: Vergrößerung: Maßstab 2 : 1 (Vergrößerungsmaßstab)
Maßstabsberechnung
Nachfolgend aufgeführt sind Beispiele für Maßstäbe.
Verkleinerung:
1 : 10 bedeutet, dass 1 mm auf der erstellten Karte in Wirklichkeit (im Original) dem Maß 10 mm = 1 cm entspricht.
1 : 100 bedeutet, dass 1 mm auf der erstellten Karte in Wirklichkeit (im Original) dem Maß 100 mm = 10 cm entspricht.
1 : 500 bedeutet, dass 1 mm auf der erstellten Karte in Wirklichkeit (im Original) dem Maß 500 mm = 50 cm entspricht.
Vergrößerung:
2 : 1 bedeutet, dass 2 cm auf der erstellten Karte in Wirklichkeit (im Original) dem Maß 1 cm entspricht.
10 : 1 bedeutet, dass 10 cm auf der erstellten Karte in Wirklichkeit (im Original) dem Maß 1 cm entspricht.
50 : 1 bedeutet, dass 50 cm auf der erstellten Karte in Wirklichkeit (im Original) dem Maß 1 cm entspricht.
Identische Abbildung:
1 : 1 bedeutet, dass 1 cm auf der erstellten Karte in Wirklichkeit (im Original) dem Maß 1 cm entspricht.
Eine Maßstabsleiste dient der Kennzeichnung des zur Erstellung einer Abbildung verwendeten Maßstabs. Mit ihr wird der auf der Karte (dem Dokument) verwendete Maßstab in Form einer Skala angegeben.
Maßstäblich vergrößern und maßstäblich verkleinern: Um eine Figur maßstäblich zu vergrößern, oder zu verkleinern werden alle Seiten der zu spiegelnden Figur mit einem positiven Faktor multipliziert. Ist dieser Faktor k < 1, so erfolgt eine Verkleinerung des Gebildes. Wird der Faktor k > 1 gewählt, so findet eine Vergrößerung der Originalfigur statt. Alle der Figur zugehörogen Winkel bleiben hierbei erhalten.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Berechnung und Darstellung

Gehen Sie folgendermaßen vor, um grundlegende geometrische Transformationen mit Figuren in diesem Modul durchzuführen:
- Legen Sie die zur Definition eines Urpolygons notwendige Punktezahl durch die Bedienung des Steuerelements Punktezahl fest.
- Geben Sie die Koordinatenwerte der Punkte des Urpolygons in die dafür vorgesehenen Felder ein. Beginnen Sie hierbei mit P1 und benutzen Sie die Eingabefelder zur Definition weiterer Punkte gemäß der Reihenfolge P2, P3, P4, P5 ....
- Wählen Sie, mit Hilfe der aufklappbaren Auswahlboxen im Formularbereich Operationen, die Arten der mit dem Urpolygon durchzuführenden Transformationen. Achten Sie hierbei darauf, dass die entsprechenden Kontrollkästchen aktiviert sind.
- Legen Sie durch die Eingabe entsprechender Zahlen in die dafür zur Verfügung stehenden Felder, zu verwendende Parameterwerte bzw. Punktkoordinaten fest.
- Bedienen Sie die Schaltfläche Berechnen.
Das Programm gibt die Koordinaten des definierten Urpolygons, wie die transformierter Objekte in der Tabelle aus. Für das Urpolygon werden die Werte folgender Eigenschaften angezeigt:- Fläche des Urpolygons
(Wurden die Punkte nicht gemäß der mathematisch positiven Richtung eingegeben, so kann der Wert für die Fläche eines Polygons negativ sein) - Eckenschwerpunkt des Urpolygons
- Umfang des Urpolygons
- Fläche des Urpolygons
- Möchten Sie sich die Resultate grafisch veranschaulichen, so bedienen Sie die Schaltfläche Darstellen.
Hinweise:
Sämtliche Werte für Winkel sind im Gradmaß einzugeben.
Wurden mehrere Operationen definiert und möchten Sie nur die erste dieser berechnen bzw. grafisch ausgeben lassen, so führen Sie dies durch, indem Sie die zu den entsprechenden Auswahlboxen gehörenden Kontrollkästchen deaktivieren. Achten Sie hierbei darauf, dass es nicht möglich ist, beispielsweise nur die erste und dritte Transformation durchführen zu lassen. Die Aktivierung der Kontrollkästchen muss von oben nach unten lückenlos erfolgen.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Bedienformular

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:
- Polygonpunkte beschriften: Darstellung der Punktbeschriftung der Polygone ein-/ausschalten
- Bezugspunkt(e) beschriften: Darstellung der Bezugspunktbeschriftung ein-/ausschalten.
Verwendete Kürzel haben hierbei folgende Bedeutung:
Spiegelpunkt bei Punktspiegelung: SP
Streckzentrum: S
Drehpunkt bei Drehung: D
Drehpunkt bei Drehstreckung: DS - Koordinaten: Anzeige der Koordinatenwerte dargestellter Punkte ein-/ausschalten
- Hilfslinien darstellen: Darstellung der Hilfslinien ein-/ausschalten
- Objekte nummerieren: Nummerierung der Polygone ein-/ausschalten (Ursprungspolygon besitzt die Nr. 0, alle weiteren, die der Abbildung entsprechende Nummer)
- Abbildungen füllen: Die Farbfüllung der Polygone ein-/ausschalten
Allgemein
Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.
Weitere Themenbereiche
Beispiel
Aufgabe:
Mit einem Dreieck, welches durch die Eckpunkte P1 (-12 / 2), P2 (-4 / 4) und P3 (2 / 10) beschrieben wird, sind aufeinanderfolgende Transformationen folgender Arten durchzuführen:
1. Spiegelung an einer Gerade, die durch die Punkte G1 (-1 / 1) und G2 (1 / 2) verläuft (Geradenspiegelung)
2. Spiegelung an Punkt SP (0 / 0) (Punktspiegelung)
3. Drehstreckung um Punkt DS (2 / 3), mit Drehwinkel 45° und Streckfaktor 2
Vorgehensweise:
Nach Festlegung der Punktezahl auf 3, der Eingabe der entsprechenden Koordinatenwerte für die Punkte P1, P2 und P3 in die Felder P1, P2 und P3, der Wahl der entsprechenden Einträge aus den Auswahlboxen Abb.1, Abb.2, Abb.3, sowie der Aktivierung der entsprechenden Kontrollkästchen und einer Bedienung der Schaltfläche Berechnen, werden folgende Ergebnisse ausgegeben:
Koordinaten des Urobjekts: P1 (-12 / 2) , P2 (-4 / 4) , P3 (2 / 10)
Koordinaten der Dreieckspunkte nach Durchführung der 1. Transformation (Geradenspiegelung):
Abbildung 1: P1 (-6,8 / 8,4) , P2 (-0,4 / 3,2) , P3 (8 / -2)
Koordinaten der Dreieckspunkte nach Durchführung der 2. Transformation (Punktspiegelung):
Abbildung 2: P1 (6,8 / 8,4) , P2 (0,4 / 3,2) , P3 (-8 / 2)
Koordinaten der Dreieckspunkte nach Durchführung der 3. Transformation (Drehstreckung):
Abbildung 3: P1 (1,58 / 10,21) , P2 (0,73 / 2,01) , P3 (-4,36 / -4,78)
Für die Eigenschaften das Urobjekts (Dreieck P1P2P3) werden zudem folgende Werte ausgegeben:
Fläche: 18 FE
Umfang: 32,856 LE
Eckenschwerpunkt: SP (-4,666 / 5,333)

Grafische Darstellung - Beispiel 1

Grafische Darstellung - Beispiel 2

Grafische Darstellung - Beispiel 3

Grafische Darstellung - Beispiel 4

Grafische Darstellung - Beispiel 5

Grafische Darstellung - Beispiel 6
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.
Wikipedia - Zentrische Streckung
Wikipedia - Drehstreckung
Wikipedia - Drehung
Wikipedia - Spiegelung
Wikipedia - Scherung
Wikipedia - Affine Abbildung
Wikipedia - Polygon
Achsenabschnittsform einer Geraden - Punkt-Richtungs-Form einer Geraden - Zwei-Punkte-Form einer Geraden - Hessesche Normalenform einer Geraden - Allgemeine Form einer Gerade - Gerade - Gerade - Gerade - Gerade - Interaktiv - Gerade - Punkt - Gerade - Punkt - Interaktiv - Geradensteigung - Kreis - Punkt - Kreis - Punkt - Interaktiv - Kreis - Gerade - Kreis - Gerade - Interaktiv - Kreis - Kreis - Kreis - Kreis - Interaktiv - Kreisausschnitt - Kreissegment - Kreisring - Ellipse - Regelmäßiges Vieleck - Viereck - Allgemeines Viereck – Interaktiv - Satz des Ptolemäus - Satz des Arbelos - Pappus-Kreise - Archimedische Kreise - Hippokrates Möndchen - Varignon-Parallelogramm - Rechteck-Scherung - Soddy-Kreise - Bewegungen in der Ebene - Affine Abbildung - Analyse affiner Abbildungen - Inversion einer Geraden am Kreis - Inversion eines Kreises am Kreis - Spirolateralkurven - Spiralen im Vieleck - Granvillesche Kurven - Bérard-Kurven - Eikurven - Kegelschnitt - Prinzip - Pyramidenschnitt - Prinzip - Kegelschnitte in Mittelpunktlage - Kegelschnitte in Mittelpunktlage - Interaktiv - Kegelschnitte in achsparalleler Lage - Kegelschnitte in achsparalleler Lage - Interaktiv - Kegelschnitte in Mittelpunktlage - Punkt - Kegelschnitte in Mittelpunktlage - Gerade - Allgemeine Kegelschnitte - Kegelschnitte durch 5 Punkte - Interaktive Geometrie mit Objekten - Winkelmaße - Strahlensatz - Teilungsverhältnis - Konstruktion einer Mittelsenkrechten - Konvexe Hülle - Dreieck - Pyramide - Quader im Raum (3D) - Krummflächig begrenzte Körper (3D) - Ebenflächig und krummflächig begrenzte Körper (3D) - Platonische Körper (3D) - Archimedische Körper (3D) - Spezielle Polyeder (3D) - Selfbuild - Punkte (3D) - Selfbuild - Strecken (3D)

Startfenster des Unterprogramms Polygone
MathProf 5.0 - Unterprogramm Affine Abbildungen

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















