MathProf - Pfadregeln - Baumdiagramm - Totale Wahrscheinlichkeit - Ereignisse

Fachthema: Pfadregel

MathProf - Stochastik - Statistik - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für Schüler, Abiturienten, Studenten, Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul mit Hilfe dessen sich der Multiplikationssatz
mehrstufiger Laplace-Experimente am Baumdiagramm veranschaulichen lässt.

Dieses Unterprogramm ermöglicht hierdurch die Durchführung der Analyse geltender Sachverhalte bzgl. der Pfadregel.

Nach einer Festlegung relevanter Werte führt der implementierte Rechner die hierfür relevanten Untersuchungen durch, gibt die ermittelten  Ergebnisse sowohl grafisch wie auch in einer Tabelle aus und ermöglicht die Analyse der entsprechenden Zusammenhänge.

 

Weitere relevante Seiten zu diesem Programm

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

 

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Videoauswahl zu MathProf 5.0.
 

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche können Sie eine kostenlose Demoversion des Programms MathProf 5.0 herunterladen.

  

Themen und Stichworte zu diesem Modul: Pfadregeln - Summenregel - Pfadregel - Mehrstufige Zufallsexperimente - Mehrstufige Zufallsversuche - Zufallsversuch - Einstufiges Zufallsexperiment - Pfade - Regeln - Pfad - Formel - Totale Wahrscheinlichkeit - Zufall und Wahrscheinlichkeit - Zusammengesetzte Zufallsexperimente - Mehrstufiges Zufallsexperiment - Zufall - Mathematik - Aufbau - Anzahl - Einstufige Zufallsexperimente - Einstufige Zufallsversuche - Zweistufige Zufallsexperimente - Baumdiagramme - Zweistufiges Baumdiagramm - Dreistufiges Baumdiagramm - Formeln - Farben - Einstufig - Mehrstufig - Satz der totalen Wahrscheinlichkeit - Laplace-Experiment - Laplace-Versuch - Laplace Experiment - Wahrscheinlichkeit - 1. Pfadregel - 2. Pfadregel - Baumdiagramm - Erste Pfadregel - Zweite Pfadregel - Wahrscheinlichkeitsrechnung - Rechner - Ergebnis - Bild - 1 - 2 - 3 - 4 - 5 - 6 - Würfel - Würfeln - Werfen - Erstellen - Beschriften - Dreistufig - Zweistufig - Zeichnen - Zahlen - Würfelzahl - Summe - Addieren - Berechnen - Plotter - Graph - Grafik - Darstellung - Berechnung - Grundlagen - Darstellen - Auswertung - Auswerten - P(a) - P(b) - P(a b) - Beispiel - Definition - Tabelle - Einführung - Was ist - Was sind - Wie viele - Wieviel - Wieviele - Welche - Welcher - Welches - Wodurch - Erklärung - Einfach erklärt - Herleitung - Beweis - Beschreibung - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Einführung - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Mathe - Mathematik - Begriff - Begriffe - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Schreibweise - Pfadwahrscheinlichkeiten - Additionsregel - Multiplikationsregel - Stochastik - Grundlagen - Grundlegendes - Pfadmultiplikationsregel - Pfadadditionsregel - Wahrscheinlichkeitsbaum - Augenzahl beim Würfeln - Augensumme - Augenzahl - Elementarereignis - Ereignis - Ereignisse - Menge - Ereignismenge - Elementarereignisse - Zufällige Vorgänge - Zufallsereignis - Zufallsereignisse - Unmögliches Ereignis - Sicheres Ereignis - Zusammengesetzte Ereignisse - Zufallsexperiment - Zufallsexperimente - Zufallsvariable - Einzelwahrscheinlichkeit - Einzelwahrscheinlichkeiten - Gesamtwahrscheinlichkeit - Abhängigkeit - Stochastisch abhängig - Stochastisch unabhängig - Stochastische Abhängigkeit - Stochastische Unabhängigkeit - Unabhängig - Unabhängigkeit - Unabhängigkeit von Ereignissen - Unabhängige Ereignisse - Möglichkeiten beim Würfeln - Augensumme beim Würfeln

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zum Inhaltsverzeichnis der in MathProf 5.0 implementierten Module bzw. zur Bestellseite für das Programm.
 

 

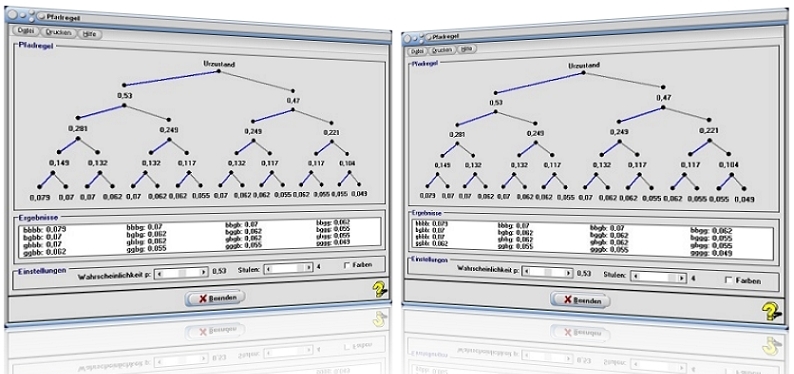
Modul Pfadregel

 
Im kleinen Zusatzmodul [Stochastik] - Pfadregel lässt sich der Multiplikationssatz mehrstufiger Laplace-Experimente (Zufallsversuche) am Baumdiagramm veranschaulichen.

Die Pfadregel (Summenregel) ermöglicht die Ermittlung der Wahrscheinlichkeit eines bestimmten Ereignisses bei der Durchführung eines mehrstufigen Zufallsexperiments. Die Wahrscheinlichkeit des Eintretens eines bestimmten Ereignisses entspricht der Summe der Wahrscheinlichkeiten aller Pfade, die zu diesem Resultat führen.
 

1. Pfadregel (Pfadmultiplikationsregel oder Multiplikationsregel):
Die 1. Pfadregel (Pfadmultiplikationsregel oder Multiplikationsregel) lautet: Die Wahrscheinlichkeit eines Elementarereignisses in einem mehrstufigen Zufallsexperiment ist gleich dem Produkt der Wahrscheinlichkeiten entlang des Pfades, der zu diesem Ergebnis im Baumdiagramm hinführt. P(D) = P(A) · P_A(D)
 
2. Pfadregel (Pfadadditionsregel oder Additionsregel):
Die 2. Pfadregel (Pfadadditionsregel oder Additionsregel) lautet: Die Wahrscheinlichkeit eines Ereignisses in einem mehrstufigen Zufallsexperiment ist die Summe der Wahrscheinlichkeiten der Pfade, die im Baumdiagramm zu diesem Ereignis gehören. P(D ∪ E) = P(D) + P(E)

Summenregel:

Die Summenregel lautet: Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe aller Einzelwahrscheinlichkeiten, welche zu diesem Ereignis führen. Diese kann durch Addition wie folgt bestimmt werden:

P(A) = P(E1 ∪ E2) = P(E1) + P(E2)
 
Bei einem Baumdiagramm haben die folgenden Pfadregeln Gültigkeit:

• Produktregel: Die gesamte Wahrscheinlichkeit eines Pfads wird mittels der Multiplikation einzelner Wahrscheinlichkeiten, die sich entlang eines Pfads befinden, berechnet.
• Summenregel: Die Wahrscheinlichkeit eines Ereignisses wird durch die Addition der einzelnen Wahrscheinlichkeiten aller Pfade gebildet, die zu dem Ereignis führen
• Verzweigungsregel: Die Summe der einzelnen Wahrscheinlichkeiten aller Äste, die von einem Verzweigungspunkt ausgehen, beträgt 1.

Dieses Unterprogramm bietet die Möglichkeit, sich die Zusammenhänge zur Bestimmung von Wahrscheinlichkeiten prinzipiell grafisch zu veranschaulichen. Eingesetzt werden kann die Pfadregel dann, wenn ein Laplace-Experiment genau 2 mögliche Elementarereignisse besitzt (z.B. Farbe blau oder grau).
 

 
Zufallsexperimente: Als Zufallsexperiment wird ein Versuch bezeichnet, bei dem mehr als ein möglicher zufälliger Ausgang existiert (bei dem mehr als ein einzelnes Ergebnis resultieren kann).

Zufallsereignisse: Bei einem Zufallsereignis handelt es sich um den Teil einer Menge von Ergebnissen eines Zufallsexperiments dem eine eintretende Wahrscheinlichkeit zugerechnet werden kann.
 
Ein Zufallsexperiment, bei welchem den einzelnen Ereignissen dieselben Wahrscheinlichkeiten zugeordnet werden können, wird als Laplace-Experiment oder (Laplace-Versuch) bezeichnet. Zufallsexperimente bestehen häufig aus einer bestimmten Anzahl von Teilexperimenten, die hintereinander ausgeführt werden. Die Ermittlung von Wahrscheinlichkeiten kann in solchen Fällen schnell unübersichtlich werden.

Einstufig: Als einstufiges Zufallsexperiment oder einstufiger Zufallsversuch wird ein Experiment bezeichnet, welches genau einmal durchgeführt wurde.

Zweistufig: Als zweistufiges Zufallsexperiment oder zweistufiger Zufallsversuch wird ein Experiment bezeichnet, welches sich aus genau zwei aufeinanderfolgenden Schritten zusammengesetzt, die ebenfalls Zufallsexperimente sind.

Mehrstufig: Als mehrstufiges Zufallsexperiment oder mehrstufiger Zufallsversuch wird ein Experiment bezeichnet, welches sich aus mehreren aufeinanderfolgenden Schritten zusammengesetzt, die ebenfalls Zufallsexperimente sind. Zufallsexperimente dieser Art werden auch als zusammengesetzte Zufallsexperimente bezeichnet.
 
Hilfe bietet hierbei die grafische Darstellung mit einem Baumdiagramm (Wahrscheinlichkeitsbaum). In einem derartigen Diagramm werden die Ausgänge eines Zufallsexperiments als Linien dargestellt und die entsprechenden Wahrscheinlichkeiten dazu geschrieben. Ein Baumdiagramm setzt sich aus einer bestimmten Anzahl von Pfaden und Stufen zusammen. Ein zweistufiges Baumdiagramm besteht aus zwei Stufen, mehrstufige Baumdiagramme setzen sich aus mehreren Stufen zusammen.
 
Zusammengesetze Zufallsexperimente bestehen aus mehreren einzeln aufeinanderfolgend ablaufenden einstufigen Zufallsexperimenten.

Als Augensumme (Augenzahl) wird die Summe aller Punkte mehrerer Würfel bezeichnet. Augen sind die Punkte der einzelnen Würfelseiten.

Als Pfadwahrscheinlichkeiten werden die einzelnen Wahrscheinlichkeiten eines mehrstufigen Zufallsexperiments bezeichnet.

Einzelwahrscheinlichkeiten: Als Einzelwahrscheinlichkeit wird die Wahrscheinlichkeit für den Ausgang eines Zufallsexperiments bezeichnet. Die Gesamtwahrscheinlichkeit ist die Summe aller Einzelwahrscheinlichkeiten.

Zufallsvariablen: Eine Zufallsvariable ist ein variable Größe, deren Werte vom Zufall abhängig sind.
  

Elementarereignis:

Elementarereignisse sind alle möglichen, einander gegenseitig ausschließenden Ausgänge eines beliebig oft wiederholbaren Versuchs bzw. Experiments. Ihre Menge wird mit E bezeichnet. Jede Teilmenge A ⊆ E heißt Ereignis, welches exakt dann eintritt, wenn eines der Elementarereignisse eintritt, aus welchen A besteht.

Unabhängigkeit (stochastische Unabhängigkeit, Unabhängigkeit von Ereignissen, unabhängige Ereignisse):

Zwei Ereignisse A und B sind stochastisch unabhängig voneinander, wenn das Eintreten eines Ereignisses keine Auswirkungen auf die Wahrscheinlichkeit des anderen hat.

Abhängigkeit (stochastische Abhängigkeit, Abhängigkeit von Ereignissen, abhängige Ereignisse):

Zwei Ereignisse A und B sind stochastisch abhängig voneinander, wenn das Eintreten eines der Ereignisse die Wahrscheinlichkeit für das Eintreten des anderen Ereignisses beeinflusst.
 
Unmögliches Ereignis:

Ein unmögliches Ereignis A ist ein Ereignis, welches bei jeder Ausführung eines Zufallsexperiments niemals eintreten kann. Die Wahrscheinlichkeit für das Eintreten eines unmöglichen Ereignisses beträgt 0 → P(A) = 0.

Sicheres Ereignis:

Ein sicheres Ereignis A ist ein Ereignis, welches bei jeder Ausführung eines Zufallsexperiments mit Sicherheit eintritt. Die Wahrscheinlichkeit für das Eintreten eines sicheren Ereignisses beträgt 1 → P(A) = 1.

Zusammengesetzte Ereignisse:

Ereignisse, die mehr als ein einzelnes Element enthalten, werden als zusammengesetzte Ereignisse bezeichnet. Bei der Bildung eines Gegenereignisses eines zusammengesetzten Ereignisses sind die De Morganschen Gesetze zu beachten.
 
Ereignismenge - Ergebnismenge:

Eine Ereignismenge ist die Teilmenge einer Ergebnismenge. Als Ergebnismenge wird die Menge aller möglichen Ereignisse A_i eines Zufallsexperiments bezeichnet, die auftreten können.
    

 
Totale Wahrscheinlichkeit:

Der Satz der totalen Wahrscheinlichkeit beschreibt die Wahrscheinlichkeit eines Ereignisses, wenn lediglich bedingte Wahrscheinlichkeiten gegeben sind. Dieser ermöglicht es, Einzelwahrscheinlichkeiten aus den bedingten Wahrscheinlichkeiten zu ermitteln. Die allgemeine Definition des Satzes für die totale Wahrscheinlichkeit (für mehrere Ereignisse) dessen lautet:


 
Für genau zwei Ereignisse A und B ist dieser wie folgt definiert:
 
P(A ) = P(B) ⋅ P(A|B) + P(B) ⋅ P(A|B)
 

Am Rollbalken mit der Bezeichnung Wahrscheinlichkeit p kann die Wahrscheinlichkeit für das Eintreten eines der beiden Ereignisse eingestellt werden (voreingestellt: p = 0.5). Mit Hilfe des Rollbalkens Stufen können Sie die Anzahl der Stufen einstellen (voreingestellt: 4).
 

An den Baumknoten werden die Wahrscheinlichkeiten des Eintretens der entsprechenden Kombination, unter Berücksichtigung der Reihenfolge des Eintretens der Elementarereignisse, angezeigt. Diese werden in der darunter angeordneten Tabelle ausgegeben, wenn das Kontrollkästchen Farben deaktiviert ist. Wird dieses Kontrollkästchen aktiviert, so wird die Reihenfolge der Ereignisse ausgegeben (Zeichenkürzel: b: blau - g: grau).
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

   
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Mathe-Leistungskurs (LK).
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
   

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

Kombinatorik

Urnenmodell

Beispiel 1 - Werfen einer Münze (Kopf oder Zahl):

Es erfolgt das zweimalige Werfen einer Münze. Die Wahrscheinlichkeit für das Werfen einer Zahl oder eines Kopfs beträgt 50% bzw. 0.5. Die Wahrscheinlichkeit dafür, dass nach zweimaligem Werfen einmal eine Zahl (blau) sowie einmal ein Kopf (grau) erscheint, resultiert aus den Wahrscheinlichkeiten zweier Pfade. Da zwei Würfe durchgeführt werden, ist der Schieberegler Stufen auf 2 zu positionieren. Unter Anwendung beider Pfadregeln ermittelt das Programm:

P(einmal Kopf und einmal Zahl)
= P(einmal Zahl - einmal Kopf)  + P(einmal Kopf - einmal Zahl)
= 0,5⋅0,5 + 0,5⋅0,5 = 0,25 +0,25
= 0,5



Die Wahrscheinlichkeit dafür, dass nach zweimaligen Werfen der Münze je einmal Kopf und Zahl geworfen wird, beträgt somit 50%.

Beispiel 2 - Augenzahl (Augensumme) beim Würfeln - Möglichkeiten beim Würfeln:

Werden die Wahrscheinlichkeiten für die vier möglichen Ergebnisse hinsichtlich erzielbarer Augenzahlen (Augensummen) nach einem zweimaligem Würfeln ermittelt, so ergeben sich folgende Resultate:

Beispiel 1


 Beispiel 2


 Beispiel 3


 Beispiel 4


 Beispiel 5

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Baumdiagramm zu finden.

Kombinatorik - Urnenmodell - Galton-Brett - Statistische Messwertanalyse - Hypothesentest - Binomialverteilung - Binomialverteilung - Interaktiv - Binomialkoeffizienten - Geometrische Verteilung - Geometrische Verteilung - Interaktiv - Poisson-Verteilung - Poisson-Verteilung - Interaktiv - Hypergeometrische Verteilung - Hypergeometrische Verteilung - Interaktiv - Stetige Verteilungen - Glockenkurve - Regressionsanalyse - Stichproben - Stichproben - Verteilungen - Lottosimulation - Vierfeldertest - Bedingte Wahrscheinlichkeit - Zusammenhang von Messwerten - Experimente - Gesetz der großen Zahlen - Berechnung von Pi (Monte-Carlo-Methode)

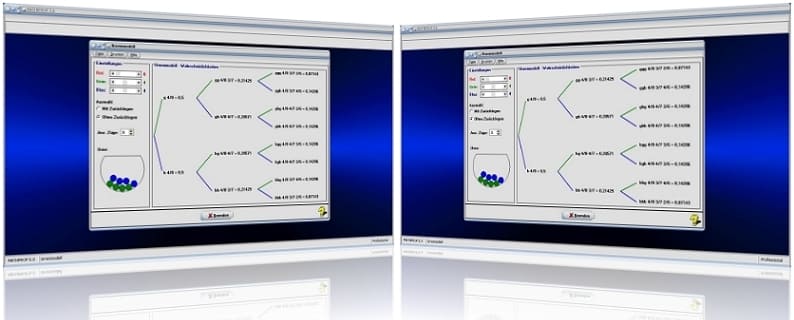
MathProf 5.0 - Unterprogramm Urnenmodelle

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

Unsere Produkte

 
Nachfolgend aufgeführt finden Sie Kurzinfos zu den von uns entwickelten Produkten.

 

I - MathProf 5.0
Mathematik interaktiv
 

MathProf 5.0 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich mathematische Sachverhalte auf einfache Weise zu verdeutlichen. Zudem spricht es diejenigen an, die sich für Mathematik interessieren, oder mathematische Probleme verschiedenster Art zu lösen haben und von grafischen 2D- und 3D-Echtzeitdarstellungen sowie Animationen beeindruckt sind.
 

 

Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.

Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
 

Kurzinfos zu Inhalten einiger Unterprogramme erhalten Sie unter:
 

• Kurzinfos zum Themengebiet Analysis
• Kurzinfos zum Themengebiet Geometrie
• Kurzinfos zum Themengebiet Algebra
• Kurzinfos zum Themengebiet 3D-Mathematik
• Kurzinfos zum Themengebiet Stochastik
• Kurzinfos zum Themengebiet Vektoralgebra
• Kurzinfos zum Themengebiet Trigonometrie
• Kurzinfos zu sonstigen Themengebieten

---

 

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Analysis eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Vektoralgebra eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in MathProf implementierten Modulen finden Sie, indem Sie den Reiter MathProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
 

 
 

 

 

II - PhysProf 1.1
Physik interaktiv
 

PhysProf 1.1 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich physikalische Gesetzmäßigkeiten und Gegebenheiten zu verdeutlichen. Es spricht alle an, die sich für die Ergründung physikalischer Prozessabläufe und derartige Zusammenhänge interessieren. In zahlreichen Unterprogrammen besteht die Möglichkeit, Veränderungen von Einflussgrößen manuell, oder durch die Ausgabe automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren. Inhaltlich umfasst es ca. 70 verschiedene Unterprogramme zu den Fachthemenbereichen Mechanik, Elektrotechnik, Thermodynamik und Optik.
 

 

Durch die Benutzung dieses Programms wird es ermöglicht, bereits bekannte Fachthemeninhalte aufzuarbeiten und entsprechende Sachverhalte numerisch wie auch grafisch zu analysieren. Mittels der freien Veränderbarkeit der Parameter von Einflussgrößen bei der Ausgabe grafischer Darstellungen besteht in vielen Unterprogrammen die Möglichkeit, Veränderungen an dargestellten Zusammenhängen manuell oder durch die Anwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
 

Eine Übersicht aller in PhysProf 1.1 zur Verfügung stehender Programmteile finden Sie im PhysProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

 

Kurzinfos zu Inhalten einiger Unterprogramme von Physprof 1.1 erhalten Sie unter:
 

• Kurzinfos zum Themengebiet Mechanik
• Kurzinfos zum Themengebiet Elektrotechnik
• Kurzinfos zum Themengebiet Optik
• Kurzinfos zum Themengebiet Thermodynamik
• Kurzinfos zu sonstigen Themengebieten

---

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in PhysProf implementierten Modulen finden Sie, indem Sie den Reiter PhysProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
 

 
 

 

 
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
 

SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.

Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.

 

 
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.

Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
 

Eine Inhaltsübersicht dessen finden Sie unter SimPlot - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

 

Beispiele einiger mit Simplot 1.0 erzeugter Grafiken finden Sie unter Beispiele, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

---

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.