MathProf - Obersummen - Untersummen - Streifenmethode

Fachthema: Ober- und Untersumme
MathProf - Analysis - Ein Programm für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Präsentation relevanter Sachverhalte mittels Simulationen, 2D- und 3D- Computeranimationen für die Schule, die Oberstufe, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur interaktiven Bildung der Ober- und Untersumme von Streifenflächen zur Analyse der Herleitung der Integralrechnung.
In diesem Teilprogramm erfolgt die Durchführung der Aufleitung unter Anwendung der Streifenmethode sowie das Berechnen der Obersumme und das Berechnen der Untersumme zur näherungsweisen Ermittlung der zwischen einer definierten Kurve und der x-Achse eingeschlossenen Fläche.
Der Rechner stellt die entsprechenden Zusammenhänge unmittelbar nach Eintritt einer interaktiven Operation dar. Jedes relevante Ergebnis einer durchgeführten Berechnung zu diesem Fachthema wird aktualisiert ausgegeben.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben, sind implementiert.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Summenbildung - Obersummen - Untersummen - Berechnen - Definition - Streifenmethode - Rechner - Plotten - Graph |
 |  |
Obersumme und Untersumme - Interaktiv

Modul Ober- und Untersummen - Interaktiv
Das Unterprogramm [Analysis] - [Integrationsverfahren] - Ober- und Untersummen - Interaktiv ermöglicht es, sich das Prinzip der Integralrechnung interaktiv verständlich machen zu können.

Bestimmte Integrale werden errechnet, indem man das zu berechnende Flächenstück, zwischen den Grenzen x1 = a und x2 = b in eine festgelegte Anzahl von Streifen (bei der hier gezeigten klassischen Methode sind dies Rechtecke) zerlegt und eine Grenzwertbildung der Obersummen und Untersummen der Streifenflächen durchführt. Dieses Verfahren zur Berechnung des bestimmten Integrals wird Streifenmethode genannt und findet unter anderem Verwendung bei der numerischen Integration.
Dieser Grenzwert wird als das bestimmte Integral einer stetigen Funktion f(x) in den Grenzen von x1 = a bis x2 = b bezeichnet.
Dieses Modul ermöglicht die Untersuchung explizit definierter Funktionen bzgl. Ober- und Untersummen innerhalb eines frei wählbaren Intervallbereichs, in Abhängigkeit einer wählbaren Anzahl von Stützstellen.
Es werden die Berechnungsergebnisse folgender Werte ausgegeben:
- Obersumme
- Untersumme
- Mittelwert (von Obersumme u. Untersumme)
- Fehlerintervall (Differenz Obersumme / Untersumme)
Darstellung

Um sich Zusammenhänge bzgl. der Bildung von Ober- und Untersummen einer stetigen Funktion f(x,p) grafisch interaktiv zu veranschaulichen, gehen Sie folgendermaßen vor:
- Definieren Sie die mathematische Funktion, mit welcher Sie Untersuchungen durchführen möchten, gemäß den geltenden Syntaxregeln im Eingabefeld mit der Bezeichnung f(x,p) =.
- Bedienen Sie die Schaltfläche Darstellen.
- Wählen Sie auf dem Bedienformular durch die Aktivierung des Kontrollschalters Obersumme, Untersumme bzw. Ober- und Untersumme, welche Art der Summenbildung durchgeführt werden soll.
- Verwenden Sie den sich auf dem Bedienformular befindenden Rollbalken Anzahl Stützstellen um die Anzahl zu verwendender Stützstellen festzulegen.
- Um den Bereich zu verändern, über welchen eine Bildung von Ober- und Untersummen durchgeführt wird, können Sie die Schaltfläche Punkte auf dem Bedienformular nutzen und die entsprechenden Werte im daraufhin erscheinenden Formular eingeben. Übernommen werden diese, wenn Sie die sich dort befindende Schaltfläche Ok bedienen.
- Möchten Sie die Bereichsgrenzen zur Bildung von Ober- und Untersummen mit der Maus verändern, so klicken Sie mit der linken Maustaste in einen der rechteckig umrahmten Mausfangbereiche und bewegen den Mauscursor bei gedrückt gehaltener Maustaste nach links oder nach rechts.
- Um sich die Kurve vor den Balken ausgeben zu lassen, aktivieren Sie das Kontrollkästchen Kurve vorne.
- Enthält der Funktionsterm das Einzelzeichen P, so legen Sie, wie unter Verwendung von Funktionsparametern beschrieben, nach einer Bedienung des Schalters Parameter P den zu durchlaufenden Wertebereich für diesen Funktionsparameter, sowie die zu verwendende Schrittweite, fest. Positionieren Sie hierauf den Schieberegler Parameter P, um den Einfluss des Parameters P zu untersuchen.
- Möchten Sie Analysen mit Hilfe von Simulationen durchführen, so wählen Sie durch Aktivierung des Kontrollschalters Stützstellen oder Parameter P die Art der Simulation die Sie ausführen lassen möchten.
Um die Anzahl von Stützstellen simulativ verändern, oder eine automatisch ablaufende Parameterwertsimulation durchführen zu lassen, klicken Sie auf die Schaltfläche Simulation.
Beendet werden kann die Ausführung einer Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.
Beachten Sie:
Führen Sie Analysen dieser Art nur mit Funktionen durch, die einen stetigen Verlauf vorweisen, bzw. legen Sie den Intervallbereich in einen Abschnitt in welchem die Funktion stetig ist, da es ansonsten zu verfälschten Ergebnissen, wie ggf. auch zu Darstellungsfehlern kommen kann.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Bedienformulare
Wurde zur Analyse der Zusammenhänge ein Funktionsterm erstellt, der kein Einzelzeichen P zur Definition eines Funktionsparameters enthält, so wird bei der Ausgabe einer grafischen Darstellung nachfolgend gezeigtes Bedienformular zur Verfügung gestellt.

Enthält der erstellte Term das Einzelzeichen P zur Definition eines Funktionsparameters, so wird bei der Ausgabe einer grafischen Darstellung das nachfolgend abgebildete Formular eingeblendet.

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:
- Bereich beschriften: Darstellung der Mausfangpunkte ein-/ausschalten
- Koordinaten: Anzeige der Koordinaten der Mausfangpunkte ein-/ausschalten
- Bereichsmarkierung: Markierung des Untersuchungsbereichs ein-/ausschalten
Allgemein
Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.
Weitere Themenbereiche
Beispiel
Bei der Ermittlung der Ober- und Untersummen für die Funktion f(x) = 3·cos(x/2)²-1, innerhalb des mit Hilfe der Schaltfläche Punkte festgelegten Bereichsintervalls von x1 = 1 bis x2 = 3, ergeben sich nach einer Eingabe des Terms 3*COS(X/2)^2-1 unter aufeinanderfolgender Verwendung verschiedener Anzahlen von Stützstellen durch die Positionierung des Rollbalkens Anzahl Stützstellen nachfolgend gezeigte Ergebnisse:
| Anzahl Stützstellen: | 5 | 10 | 50 |
| Obersumme: | 0,422 | 0,182 | -0,004 |
| Untersumme: | -0,495 | -0,276 | -0,096 |
| Mittelwert: | -0,036 | 0,047 | 0,050 |
| Fehlerintervall D: | 0,9181 | 0,459 | 0,091 |
Es ist zu entnehmen, dass sich das Fehlerintervall D mit einer Erhöhung der Anzahl von Stützstellen reduziert und Ober- und Untersumme sich somit dem exakten Wert für den Flächeninhalt des Bereichs unter der Kurve nähern.

Grafische Darstellung - Beispiel 1

Grafische Darstellung - Beispiel 2

Grafische Darstellung - Beispiel 3

Grafische Darstellung - Beispiel 4

Grafische Darstellung - Beispiel 5

Grafische Darstellung - Beispiel 6
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Riemannsches Integral zu finden.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Segmentweise definierte Funktionen - Kurvenscharen - Funktionsparameteranalyse - Funktionswertetabellen - Iteration - Parameter der Sinus- und Cosinusfunktion - Parameter der Logarithmusfunktion - Parameter der Betragsfunktion - Parameter der Integer-Funktion - Parameter der Quadratwurzelfunktion - Parameter der Potenzfunktion - Parameter der Exponentialfunktion - Kubische Funktion in allgemeiner Form - Kubische Funktion in spezieller Form - Zahlenfolgen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Rekursive Zahlenfolgen - Interaktiv - Arithmetische und geometrische Zahlenfolgen - Parabelgleichungen - Parabelgleichungen - Interaktiv - Parabel und Gerade - Interaktiv - Analyse quadratischer Funktionen - Ermittlung ganzrationaler Funktionen - Ganzrationale Funktionen (Polynome) - Ganzrationale Funktionen (Polynome) - Interaktiv - Gebrochenrationale Funktionen - Gebrochenrationale Funktionen - Interaktiv - Interpolation nach Newton und Lagrange - Interpolation ganzrationaler Funktionen - Polynomregression - Nullstellen - Iterationsverfahren - Horner-Schema - Tangente - Normale - Tangente - Sekante - Tangente und Normale von externem Punkt - Kurvendiskussion - Kurvendiskussion - Interaktiv - Obersummen und Untersummen - Integrationsmethoden - Rotationsparaboloid (3D) - Integralrechnung - Integralrechnung - Interaktiv - Zykloide - Hypozykloide - Epizykloide - Sternkurven - Zissoide - Strophoide - Kartesisches Blatt - Semikubische Parabel - Archimedische Spirale - Logarithmische Spirale - Fourier-Summen - Fourier-Reihen - Taylorreihen und Potenzreihen - Implizite Funktionen
Startfenster des Unterprogramms Ober- und Untersummen - Interaktiv
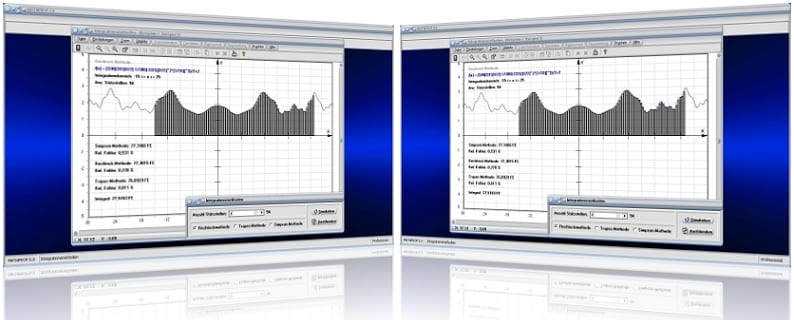
MathProf 5.0 - Unterprogramm Integrationsmethoden

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.