MathProf - Nullstellen - Verfahren - Newton - Rechner

Fachthemen: Verfahren - Nullstellen - Bisektionsverfahren - Regula falsi - Sekantenverfahren - Bisektionsmethode - Iterationsverfahren - Intervallhalbierung - Methode - Newton-Verfahren
MathProf - Analysis - Ein Programm für Mathematik zum Lösen verschiedenster Aufgaben und zur Anwendung numerischer Methoden und Verfahren. Eine Software zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Analyse verschiedener Iterationsverfahren (Approximationsverfahren), welche zum numerischen Berechnen der Näherungswerte der Nullstellen mathematischer Funktionen verwendet werden.
In diesem Unterprogramm wird die Nullstellenberechnung unter Verwendung unterschiedlicher numerischer Verfahren (Algorithmen) ermöglicht. Hierzu zählen unter anderem das Newtonsche Näherungsverfahren, das Sekantenverfahren sowie das Bisektionsverfahren.
Der implementierte Nullstellen-Rechner ermöglicht die Analyse der zuvor beschriebenen numerischen Näherungsmethoden zur Bestimmung der Schnittpunkte einer Funktion mit der x-Achse und die Darstellung der entsprechenden Zusammenhänge.
Die Ausgabe der Werte ermittelter Ergebnisse erfolgt zur Echtzeit. Jedes relevante Ergebnis einer durchgeführten Berechnung zu diesem Fachthema wird aktualisiert ausgegeben.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls zur numerischen Differentiation geben, sind eingebunden.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Nullstellen - Numerik - Methoden - Verfahren - Iterationsverfahren - Algorithmus - Algorithmen - Newton - Schema - Newton-Verfahren - Numerisch - Näherungsverfahren - Bisektionsverfahren - Newtonsches Näherungsverfahren - Regula falsi - Regula falsi-Methode - Sekantenverfahren - Formel - Näherung - Fixpunktiteration - Newtonverfahren - Approximation - Intervallhalbierungsverfahren - Halbierungsverfahren - Newton Iteration - Näherungswert - Näherungswerte - Nullstellenberechnung - Tangentenverfahren - Nullstellensuche - Nullstellenbestimmung - Numerische Mathematik - Numerische Verfahren - Numerische Differentiation - Nullstellen-Approximation - Brent-Verfahren - Brent-Methode - Intervallschachtelung - Intervallhalbierung - Numerische Bestimmung - Numerische Methoden - Rechnerisch - Berechnung - Schema - Begriff - Begriffe - Computer - Software - Programm - Beispiel - Finden - Bestimmen - Bestimmung - Nullstellen finden - Untersuchen - Untersuchung - Interpolationsverfahren - Numerisch - Grafisch - Lösung - Lösen - Approximationsverfahren - Newtonsches Verfahren - Interpolation - Iterationsformel - Plotter - Graph - Plotten - Bild - Grafik - Herleitung - Beweis - Tabelle - Erklärung - Einfach erklärt - Beschreibung - Bedeutung - Was bedeutet - Welche - Welcher - Welches - Wodurch - Definition - Einführung - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Mathe - Mathematik - Anwendungsaufgaben - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Beispiele - Rechner - Berechnen - Darstellung - Darstellen - Lösungsverfahren - Nullstellenproblem - Nullstellenverfahren - Konvergenz - Konvergenzbedingung - Satz von Bolzano - Nullstellensatz - Zwischenwertsatz |
Näherungsverfahren zur Berechnung von Nullstellen

Modul Nullstellen - Iterationsverfahren
Mit Hilfe des kleinen Unterprogramms [Analysis] - [Nullstellen] - Nullstellen - Iterationsverfahren können verschiedene Näherungsverfahren zur Ermittlung (zum Finden) von Nullstellen mathematischer Funktionen (Nullstellenbestimmung - Numersiche Nullstellensuche) untersucht und verglichen werden.

Als Nullstelle einer Funktion wird die Stelle bezeichnet, bei der die Kurve einer Funktion die Abszisse (x-Achse) berührt oder schneidet. Zur Berechnung der Nullstellen mathematischer Funktionen kommen unter anderem numerische Methoden zum Einsatz.
Iterationsverfahren (Näherungsverfahren) führen einen Prozess der mehrfachen Wiederholung der gleichen bzw. ähnlichen Handlung zur Ermittlung an eine Lösung durch Annäherung aus. Verfahren (Nullstellenverfahren) der in diesem Programmteil gezeigten Art werden insbesondere dann verwendet, wenn eine analytische Bestimmung von Nullstellen nicht möglich ist.
Es handelt sich hierbei um Verfahren, die die schrittweise Anwendung eines Rechenvorgangs durchführen um hierdurch näherungsweise die Lösung einer Gleichung bestimmen zu können. Als konvergierend wird eine Iteration bezeichnet, wenn mittels der Anwendung des entsprechenden Algorithmus eine Näherungslösung gefunden werden kann.
In diesem Modul stehen folgende Verfahren zur Durchführung der Nullstellenberechnung zur Auswahl:
- Newton-Verfahren (Newtonsches Näherungsverfahren)
- Regula falsi (2. Art)
- Bisektions-Verfahren (Intervallhalbierungsverfahren)
- Sekanten-Methode (Sekantenverfahren)
- Brent-Methode (Brent-Verfahren)
Hierbei stehen zwei nebeneinander angeordnete, aufklappbare Auswahlboxen zur Verfügung, um Näherungsverfahren zu selektieren. Somit wird es ermöglicht, Vergleiche zwischen den Verfahren bzgl. derer Iterationsmethodik anzustellen.

Nachfolgend wird kurz auf die vier meist verwendeten Approximationsverfahren zur Bestimmung der Nullstellen von Funktionen eingegangen. Hierzu zählen das Bisektionsverfahren (Intervallhalbierungsverfahren), das Sekantenverfahren (Regula falsi) sowie das Newtonsche Tangentenverfahren (Newton Verfahren).
I - Bisektionsverfahren - Intervallhalbierungsverfahren (Intervallhalbierungsmethode)
Das Bisektionsverfahren (Intervallhalbierungsverfahren oder Halbierungsverfahren) erzeugt unter Anwendung der Intervallhalbierung eine endliche Anzahl von Intervallen. Diese entstehen hierbei jeweils durch die Bildung der Hälfte des vorherigen Intervalls. Hierdurch können unter bestimmten Voraussetzungen unter anderem die Nullstellen einer im entsprechenden Untersuchungsbereich stetigen Funktion ermittelt werden.
II - Regula falsi - Sekantenverfahren
Die Regula Falsi-Methode (das Sekantenverfahren) ist ein Verfahren zur numerischen Berechnung von Nullstellen. Es werden Sekanten an die Funktion gelegt deren Schnittpunkt mit der Abszisse sich bei jeder Iteration der gesuchten Nullstelle nähert. Aus zwei Funktionswerten, die unterschiedliche Vorzeichen besitzen wird der Schnittpunkt der Sehne mit der Abszisse ermittelt. Dieser ermittelte Näherungswert für die Nullstelle der Funktion wird erneut verwendet und ein weiterer Funktionswert wird derart bestimmt, dass die Funktionswerte weiterhin über unterschiedliche Vorzeichen verfügen. Diese Methode wird wiederholt eingesetzt um den nächsten Näherungswert für die Nullstelle bestimmen zu können.
Hinweis: Auf das oben aufgeführte Verfahren Regula falsi 2. Art wird hier nicht eingegangen. Es handelt sich um eine optimierte Methode des in diesem Abschnitt beschriebenen Sekantenverfahrens.
III - Newtonsches Tangentenverfahren - Newtonsches Näherungsverfahren - Newtonverfahren
Newtonsches Tangentenverfahren (Newtonsches Näherungsverfahren, Newton-Verfahren, Newton Iteration, Newtonsches Verfahren oder Newtonverfahren):
Zunächst werden innerhalb des vorgegebenen Untersuchungsbereichs Bereiche bestimmt bei denen ein Vorzeichenwechsel auftritt. In einem derartigen Bereich existiert gemäß dem Zwischenwertsatz wenigstens eine reelle Nullstelle. In jedem auf diese Weise ermittelten Bereich kommt das nachfolgend beschriebene Verfahren zum Einsatz.
Die grundlegende Basis des Newtonverfahrens besteht darin, eine Tangente zu bestimmen, die sich in der Nähe einer Nullstelle der zu untersuchenden Funktion befindet. Hierauf wird die Nullstelle dieser Tangente verwendet, um mit dieser eine derartige Approximation erneut durchzuführen und als verbesserte Näherung der Nullstelle der Funktion zu verwenden. Dieser zuletzt ermittelte Näherungswert dient als Ausgangspunkt für weitere Schritte dieser Art.
Durch wiederholtes Einsetzen des zuletzt ermittelten Ergebnisses in die Newton-Formel (wiederholtes Durchführen des zuletzt beschriebenen Vorgangs) kann eine Näherung erzielt werden.
Durch die Festlegung eines geeigneten Startwerts x0 können mit Hilfe des Newtonschen Tangentenverfahrens Näherungswerte für die gesuchte Lösung einer Gleichung der Form f(x) = 0 ermittelt werden. Die hierbei angewandte Iterationsvorschrift lautet:
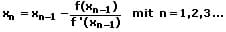
Sie wird als Iterationsformel bezeichnet.
Konvergenzbedingung (Konvergenz): Die Folge der hierdurch ermittelten Näherungswerte x0, x1, x2 ... konvergiert in diesem Fall gegen die Lösung der Gleichung f(x) = 0, wenn im Intervall [a,b], in dem sich alle Näherungswerte befinden, die nachfolgende Bedingung erfüllt ist:
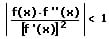
iV - Brent-Methode - Brent-Verfahren
Bei der Brent-Methode (dem Brent-Verfahren) handelt es sich um ein Verfahren, welches zur iterativen Ermittlung einer Nullstelle verwendet wird und welches das Bisektionverfahren, das Sekantenverfahren sowie die inverse quadratische Interpolation miteinander verknüpft. Dieses Verfahren wurde 1973 von Richard P. Brent entwickelt. Es handelt sich um eine Neugestaltung des ursprünglich von Theodorus Dekker 1969 entwickelten Algorithmus.
Nullstellensatz - Zwischenwertsatz - Satz von Bolzano
Zwischenwertsatz:
Der Zwischenwertsatz findet zum Nachweis von Nullstellen einer Funktion Anwendung. Zugleich gibt er Auskunft darüber, ob eine Gleichung innerhalb eines bestimmten Intervalls eine Lösung besitzt. Er besagt:
Eine in einem abgeschlossenen Intervall [a,b] stetige Funktion f nimmt jeden Wert zwischen f(a) und f(b) mindestens einmal in (a,b) an.
Nullstellensatz (Satz von Bolzano):
Eine Nullstelle x0 einer Funktion f ist der Wert aus dem Definitionsbereich bei dem der Funktionswert verschwindet, f(x0) = 0. Der Nullstellensatz besagt:
Eine auf dem abgeschlossenen Intervall [a,b] stetige Funktion mit f(a)·f(b) < 0 besitzt in (a,b) mindestens eine Nullstelle x0 ungerader Ordnung a < x0 < b mit f(x0) = 0.
Berechnung und Darstellung
Um zwei der oben aufgeführten Verfahren mit Hilfe dieses Moduls zu vergleichen, gehen Sie folgendermaßen vor:
- Definieren Sie im Eingabefeld mit der Bezeichnung f(x) = die mathematische Funktion für welche Sie die Berechnung durchführen lassen möchten.
- Wählen Sie zwei zu vergleichende Verfahren aus den aufklappbaren Auswahlboxen.
- Legen Sie den Intervallbereich (Startintervall) fest, innerhalb dessen eine Nullstelle der Funktion gesucht werden soll. Tun Sie dies durch die Eingabe entsprechender Zahlenwerte in die dafür zur Verfügung stehenden Felder (Untersuchungsbereich von x1 = und bis x2 =).
- Geben Sie in das Feld Max. Stellenzahl den ganzzahligen Wert zur Festlegung der Anzahl maximal durchzuführender Iterationsschritte ein (voreingestellt: 100).
- Bedienen Sie die Schaltfläche Berechnen.
- Um sich die Funktion und die ermittelten Iterationsstellen grafisch ausgeben zu lassen, bedienen Sie die Schaltfläche Darstellen.
Die Näherungswerte werden mitsamt derer zugehöriger Ordinatenwerte in den Tabellen ausgegeben. Ist schlechte Konvergenz oder Divergenz vorhanden und wird die vorgegebene Anzahl durchzuführender Schritte erreicht, so bricht das Programm die Iteration ab. Ist die definierte Funktion nicht differenzierbar, so wird eine entsprechende Meldung ausgegeben.
Beachten Sie:
Zwischen den Grenzen des Startintervalls muss die zu untersuchende Funktion eine Nullstelle besitzen und die Funktionswerte an diesen Stellen müssen entgegengesetzte Vorzeichen besitzen! Ist dies nicht der Fall, so erhalten Sie eine entsprechende Fehlermeldung. Vor der Durchführung von Berechnungen können Sie die Einhaltung dieser Bedingung jedoch überprüfen, indem Sie sich die zu analysierende Funktion darstellen lassen.
Hinweis:
Diese Berechnungen werden mit einer Stellengenauigkeit von 6 Nachkommastellen durchgeführt, d.h ein ermittelter Abszissenwert wird als Nullstelle akzeptiert, wenn dieser bis auf die 6. Nachkommastelle dem numerischen Wert 0 entspricht.
Als Fixpunktiteration wird ein iteratives Verfahren bezeichnet, welches zur näherungsweisen Bestimmung der Nullstellen einer Funktion innerhalb eines bestimmten Intervalls [a,b] eingesetzt wird. Jedes Verfahren dieser besitzt die Form
xk+1 = φ(xk) mit k = 0, 1, 2 ...
mit der Iterationsvorschrift φ.
Bei der Umsetzung eines derartigen Verfahrens gilt es, die Iterationsvorschrift φ in dieser Form aufzubauen, dass sie exakt einen Fixpunkt x* besitzt und somit gilt: x* = φ(x*).
Als Fixpunktiteration kann unter anderem das Newton-Verfahren betrachtet werden.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Bedienformular

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:
- Punkte: Darstellung der ermittelten Punkte des jeweils angewandten Verfahrens ein-/ausschalten
- Nummerierung: Nummerierung der ermittelten Punkte des jeweils angewandten Verfahrens ein-/ausschalten
- U-Bereich mark.: Markierung des Untersuchungsbereichs ein-/ausschalten
Allgemein
Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.
Weitere Themenbereiche
Beispiel
Bei einer Untersuchung der Funktion f(x) = x²-2 auf Nullstellen im Bereich von -2 ≤ x ≤ 0,5 unter der Verwendung der Methoden Brent-Verfahren und Bisektionsverfahren (Intervallhalbierungsverfahren), sowie einer Begrenzung der Anzahl maximal durchzuführender Schritte auf 100, kann nach einer Eingabe des Terms X^2-2 und einer Durchführung der erforderlichen Berechnungen festgestellt werden:
Diese Funktion besitzt eine Nullstelle beim Abszissenwert x = -1,41421. Bei Anwendung des Bisektions-Verfahren waren 22 Schritte notwendig um diese Nullstelle zu ermitteln. Bei Verwendung der Brent-Methode wurden hingegen lediglich 5 Iterationsschritte durchlaufen um diese Nullstelle aufzufinden.

Grafische Darstellung - Beispiel 1

Grafische Darstellung - Beispiel 2

Grafische Darstellung - Beispiel 3

Grafische Darstellung - Beispiel 4
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden:
Wikipedia - Nullstelle
Wikipedia - Newton-Verfahren
Wikipedia - Gauß-Newton-Verfahren
Wikipedia - Regula falsi
Wikipedia - Bisektion
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Segmentweise definierte Funktionen - Kurvenscharen - Funktionsparameteranalyse - Funktionswertetabellen - Iteration - Parameter der Sinus- und Cosinusfunktion - Parameter der Logarithmusfunktion - Parameter der Betragsfunktion - Parameter der Integer-Funktion - Parameter der Quadratwurzelfunktion - Parameter der Potenzfunktion - Parameter der Exponentialfunktion - Kubische Funktion in allgemeiner Form - Kubische Funktion in spezieller Form - Zahlenfolgen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Rekursive Zahlenfolgen - Interaktiv - Arithmetische und geometrische Zahlenfolgen - Parabelgleichungen - Parabelgleichungen - Interaktiv - Parabel und Gerade - Interaktiv - Analyse quadratischer Funktionen - Ermittlung ganzrationaler Funktionen - Ganzrationale Funktionen (Polynome) - Ganzrationale Funktionen (Polynome) - Interaktiv - Gebrochenrationale Funktionen - Gebrochenrationale Funktionen - Interaktiv - Interpolation nach Newton und Lagrange - Interpolation ganzrationaler Funktionen - Polynomregression - Horner-Schema - Tangente - Normale - Tangente - Sekante - Tangente und Normale von externem Punkt - Kurvendiskussion - Kurvendiskussion - Interaktiv - Obersummen und Untersummen - Obersummen und Untersummen - Interaktiv - Integrationsmethoden - Rotationsparaboloid (3D) - Integralrechnung - Integralrechnung - Interaktiv - Zykloide - Hypozykloide - Epizykloide - Sternkurven - Zissoide - Strophoide - Kartesisches Blatt - Semikubische Parabel - Archimedische Spirale - Logarithmische Spirale - Fourier-Summen - Fourier-Reihen - Taylorreihen und Potenzreihen - Implizite Funktionen
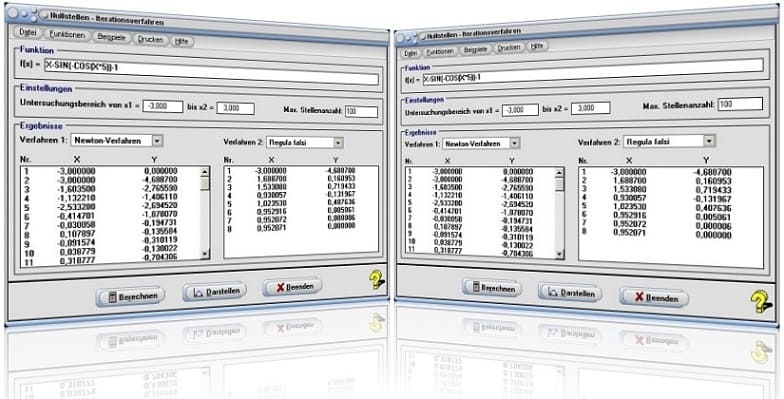
Startfenster des Unterprogramms Nullstellen - Iterationsverfahren
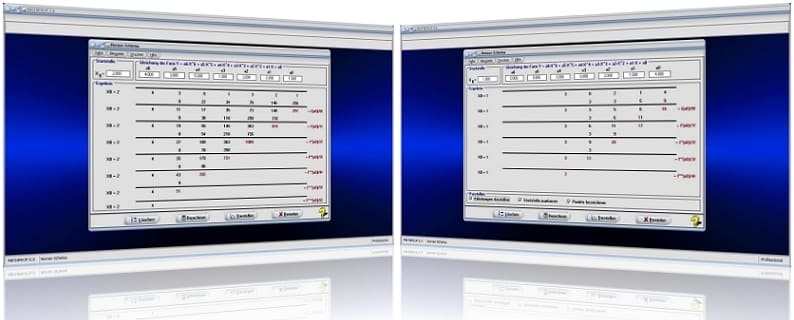
MathProf 5.0 - Unterprogramm Horner-Schema

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.