MathProf - Funktionsgraphen - Verkettung - Funktionen - Ableitung

 

Modul Mathematische Funktionen II

---

 
Das Unterprogramm [Analysis] - Mathematische Funktionen II ist implementiert, um Untersuchungen mit Optionen mathematischer Funktionen in expliziter Form durchführen zu können und diese zu plotten.

 

Möchten Sie grafische Analysen mit einem oder zwei Funktionstermen durchführen und sich diese darstellen lassen (zu plotten), so stehen hierzu folgende Optionen zur Verfügung.

 

Plotten der
 

• Funktion f(x,p)
• 1. Ableitungsfunktion (1. Ableitung) f'(x,p) von f(x,p)
• 2. Ableitungsfunktion (2. Ableitung) f''(x,p) von f(x,p)
• Umkehrfunktion (Umkehrkurve - Inverse Funktion) fu(x,p) von f(x,p)
• Krümmungskurve fk(x,p) von f(x,p)
• Spiegelung von f(x,p) an der y-Achse →  f(-x,p)
• Spiegelung von f(x,p) an der x-Achse →  -f(x,p)
• Spiegelung von f(x,p) am Koordinatenursprung → -f(-x,p)
• doppelten Anwendung der Funktionsargumente auf Funktion f(x,p) → f(f(x,p))
• Stammfunktion F(x,p)+C von f(x,p) mit Konstantenwert C = 0
• Evolute fe(x,p) von f(x,p) (Kurve der Krümmungsmittelpunkte)
   
• Funktion g(x,p)
• 1. Ableitungsfunktion (1. Ableitung) g'(x,p) von g(x,p)
• 2. Ableitungsfunktion (2. Ableitung) g''(x,p) von g(x,p)
• Umkehrfunktion (Umkehrkurve - Inverse Funktion) gu(x,p) von g(x,p)
• Krümmungskurve gk(x,p) von g(x,p)
• Spiegelung von g(x,p) an der y-Achse → g(-x,p)
• Spiegelung von g(x,p) an der x-Achse → -g(x,p)
• Spiegelung von g(x,p) an Koordinatenursprung → -g(-x,p)
• doppelten Anwendung der Funktionsargumente auf Funktion g(x,p) → g(g(x,p))
• Stammfunktion G(x,p)+C von g(x,p) mit Konstantenwert C = 0
• Evolute ge(x,p) von g(x,p) (Kurve der Krümmungsmittelpunkte)

Zudem können Sie sich Funktionsverknüpfungen (Verkettung von Funktionen) folgender Formen ausgeben lassen:

• Addition zweier Funktionen: f(x,p) + g(x,p)
• Subtraktion zweier Funktionen: f(x,p) - g(x,p)
• Multiplikation zweier Funktionen: f(x,p) · g(x,p)
• Division zweier Funktionen: f(x,p) / g(x,p)

Weiterhin wird (eingeschränkt) ermöglicht:
 

• Bildung der 1. und 2. analytischen Ableitung einer Funktion f(x)

• Bildung der 1. und 2. analytischen Ableitung einer Funktion g(x)
   

Bei Durchführung einer Parametervariation können relevante Sachverhalte bei dargestellten Funktionen interaktiv analysiert und ausgewertet werden.

 

 

Der in diesem Modul implementierte Funktionsplotter (Funktionenplotter) ermöglicht bei einer Aktivierung der entsprechenden Kontrollkästchen die Darstellung (das Zeichnen) der nachfolgend aufgeführten Arten von Funktionsgraphen:
 
Für die im oberen Eingabefeld definierte Funktion f(x,p):

Funktion f(x,p): Darstellung der Funktion f(x,p)
1. Ableitung f'(x,p): Darstellung der 1. Ableitung der Funktion f(x,p)
2. Ableitung f''(x,p): Darstellung der 2. Ableitung der Funktion f(x,p)
Umkehrfunktion fu(x,p): Darstellung der Umkehrkurve (inversen Funktion) der Funktion f(x,p)
Krümmungsfunktion fk(x,p): Darstellung der Krümmungskurve der Funktion f(x,p)
f(-x,p): Darstellung der an der y-Achse gespiegelten Kurve, welche durch einen Term der Form y = f(x,p) beschrieben wird
-f(x,p): Darstellung der an der x-Achse gespiegelten Kurve, welche durch einen Term der Form y = f(x,p) beschrieben wird
-f(-x,p): Darstellung der am Koordinatenursprung gespiegelten Kurve, welche durch einen Term der Form y = f(x,p) beschrieben wird
f(f(x,p)): Darstellung einer Kurve bei doppelter Anwendung der Funktionsargumente auf die Funktion, welche durch einen Term der Form y = f(x,p) beschrieben wird
Stammfunktion F(x,p): Darstellung der Stammfunktion F(x,p) der Funktion f(x,p) mit C = 0
Evolute fe(x,p): Darstellung der Evolute (Kurve der Krümmungsmittelpunkte) der Funktion f(x,p)
  
Für die im unteren Eingabefeld definierte Funktion g(x,p):

 
Funktion g(x,p): Plotten der Funktion g(x,p)
1. Ableitung g'(x,p): Plotten der 1. Ableitung der Funktion g(x,p)
2. Ableitung g''(x,p): Plotten der 2. Ableitung der Funktion g(x,p)
Umkehrfunktion gu(x,p): Plotten der Umkehrkurve (inverse Funktion) der Funktion g(x,p)
Krümmungsfunktion gk(x,p): Plotten der Krümmungskurve der Funktion g(x,p)
g(-x,p): Plotten der an der y-Achse gespiegelten Kurve, welche durch einen Term der Form y = g(x,p) beschrieben wird
-g(x,p): Plotten der an der x-Achse gespiegelten Kurve, welche durch einen Term der Form y = g(x,p) beschrieben wird
-g(-x,p): Plotten der am Koordinatenursprung gespiegelten Kurve, welche durch einen Term der Form y = g(x,p) beschrieben wird
g(g(x,p)): Plotten einer Kurve bei doppelter Anwendung der Funktionsargumente auf die Funktion, welche durch einen Term der Form y = g(x,p) beschrieben wird
Stammfunktion G(x,p): Plotten der Stammfunktion G(x,p) der Funktion g(x,p) mit C = 0
Evolute ge(x,p): Plotten der Evolute (Kurve der Krümmungsmittelpunkte) der Funktion g(x,p)

 

 

Ableitungsfunktionen:
 
Eine Ableitungsfunktion (1. Ableitung oder Ableitung) der Form y' = f'(x) ordnet jeder Stelle x aus einem Intervall einer Funktion der Form f(x) den Steigungswert der dortigen Kurventangente in Form eines Funktionswerts zu. Die zweite Ableitung (2. Ableitung) einer Funktion der Form y'' = f''(x) beschreibt das Krümmungsverhalten dieser Funktion.

Ableitungsgraphen: Mit dem Begriff Ableitungsgraph wird die grafische Darstellung des Kurvenverlaufs der 1. Ableitung einer mathematischen Funktion bezeichnet.
 
Umkehrfunktion (Inverse Funktion) - Umkehrbarkeit:
 
Eine Funktion heißt umkehrbar, wenn jedes Argument dieser einen einzigartigen Funktionswert hat, bzw. wenn die umgekehrte Zurodnung x = g(y) eindeutig ist. Eine Umkehrfunktion wird durch das Symbol f^-1(x) gekennzeichnet. Sie wird auch als inverse Funktion oder Inverse einer Funktion bezeichnet.

Umkehrbar sind alle streng monoton wachsenden oder fallenden Funktionen. Bei der Umkehrung einer Funktion werden deren Werte- und Definitionsbereich vertauscht. Der Graph einer Umkehrfunktion ergibt sich durch die Spiegelung des Graphen einer Funktion an der Winkelhalbierenden des ersten und dritten Quadranten, bzw. durch eine Spiegelung der Funktionskurve an der Gerade y = x.
 
Vorgehensweise zur Bestimmung einer Umkehrfunktion: Die entsprechende Funktionsgleichung y = f(x) ist nach der Variablen x aufzulösen → x = g(y). Hiernach werden die beiden Variablen x und y vertauscht.




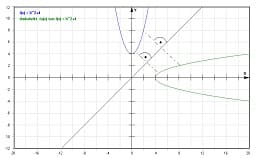
Graph einer Funktion:

Als Graph einer Funktion wird die Darstellung einer mathenmatischen Funktion bezeichnet, die den Verlauf dieser charakterisiert (grafisch darstellt). Er kann prinzipiell als die Menge der Punkte angesehen werden, die sich bezüglich der x-Achse innnerhalb des Definitionsbereichs dieser Funktion befinden und deren y-Koordinatenwerte die Funktionswerte dieser beschreiben.
 
Krümmungskurve:
 
Eine Krümmungskurve beschreibt die Richtungsänderung einer Funktion bei ihrem Durchlaufen.

Stammfunktion:
 
Die Stammfunktion F(x) einer Funktion f(x) beschreibt eine Funktion, deren erste Ableitung F'(x) die Eigenschaften der Funktion f(x) besitzt. Sie ist eine Aufleitung von f(x). Mathematisch wird der Sachverhalt wie folgt beschrieben:


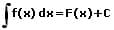
Evolute:
 
Die Evolute einer Kurve ist die Menge aller ihrer Krümmungsmittelpunkte. Die Tangenten einer Evolute sind gleichzeitig die Normalen der entsprechenden Kurve.

Verkettung von Funktionen - Verknüpfung von Funktionen:
 
Unter dem Begriff Verkettung (Komposition) mathematischer Funktionen wird deren Hintereinanderschaltung verstanden. Diese Art der Verkettung wird auch als Verknüpfung von Funktionen bezeichnet. Durch Verknüpfen (Verketten) lassen sich Funktionen addieren, subtrahieren, multiplizieren sowie dividieren.
 
Funktionen addieren - Die Addition zweier Funktionen f(x) und g(x) erfolgt in folgender Form: f(x,p) + g(x,p)
Funktionen subtrahieren - Die Subtraktion zweier Funktionen f(x) und g(x) erfolgt in folgender Form: f(x,p) - g(x,p)
Funktionen multiplizieren - Die Multiplikation zweier Funktionen f(x) und g(x) erfolgt in folgender Form: f(x,p) · g(x,p)
Funktionen dividieren - Die Division zweier Funktionen f(x) und g(x) erfolgt in folgender Form: f(x,p) / g(x,p)

Funktionen, die hinereinandergeschaltet wurden, tragen die Bezeichnung verkettete Funktionen oder verknüpfte Funktionen. Als Differenzfunktion von f(x) und g(x) wird die Funktion d(x) = f(x) - g(x) bezeichnet.

Spiegelung einer Funktion (Achsenspiegelung - Punktspiegelung):
 
Funktion spiegeln: Der Graph einer Funktion kann an den Achsen des Koordinatensystems gespiegelt werden. Durch die Anwendung der Funktionsvorschrift -f(x) wird der Graph einer Funktion der Form f(x) an der x-Achse gespiegelt. Die Spiegelung (das Spiegeln) einer derartigen Funktion an der y-Achse erfolgt durch die Verwendung der Vorschrift f(-x). Die Verwendung der Funktionsvorschrift -f(-x) bewirkt die Spiegelung des Graphen einer mathematischen Funktion der Form f(x) am Koordinatenursprung (Punktspiegelung).

Umkehrbarkeit: Eine Funktion wird als umkehrbar eindeutige Funktion bezeichnet, wenn nicht lediglich jedem ihrer Argumente ein Funktionswert in eindeutiger Form zugeordnet ist, sondern wenn jedes ihrer Funktionswerte exakt ein Argument besitzt.

Konkave Funktion: Eine Funktion wird als konkav bezeichnet, wenn sich eine zwischen zwei beliebigen Punkten dieser Funktion befindende Verbindungsgerade vollständig unterhalb der Funktion befindet oder sich mit ihr deckt.

Konvexe Funktion: Eine Funktion wird als konvex bezeichnet, wenn sich eine zwischen zwei beliebigen Punkten dieser Funktion befindende Verbindungsgerade vollständig oberhalb der Funktion befindet oder sich mit ihr deckt.

Kehrwertfunktion: Bei einer Kehrwertfunktion handelt es sich nicht um eine Umkehrfunktion, sondern die Variablen x und y einer derartigen Funktion werden nicht getauscht.  Bei einer Umkehrfunktion wird f(x) = y zu f(y) = x. Bei einer Kehrwertfunktion hingegen wird f(x) = y zu f(x) = 1⁄y.

Reziproke Funktion: Als reziproke Funktion wird der Kehrwert einer Funktion bezeichnet. Es gilt: g(x) = 1/f(x). Eine reziproke Funktion entspricht nicht einer Umkehrfunktion.

Transformation von Funktionen: Unter dem Begriff Transformation wird die Umwandlung einer Funktion verstanden. In solch einem Fall erfolgt ihre geometrische Transformation beispielsweise mittels der Durchführung einer der nachfolgend aufgeführten Maßnahmen.

- Spiegelung des Graphen der Funktion
- Verschiebung des Graphen der Funktion
- Skalierung des Graphen der Funktion

Evolute: Als Evolute einer ebenen Kurve wird die Bahn bezeichnet, auf der sich der Krümmungskreismittelpunkt bewegt, wenn der entsprechende Punkt die gegebene Kurve durchläuft.
 
 

 
Symmetrie von Funktionen: Mathematische Funktionen (in expliziter Form) können zwei unterschiedliche Arten von Symmetrie aufweisen. Hierbei handelt es sich um die Punktsymmetrie sowie die Achsensymmetrie zu einer vertikalen Achse. Eine Funktion die eine dieser beiden Eigenschaften aufweist, wird als symmetrische Funktion bezeichnet.
 
Punktsymmetrische Funktion: Eine Funktion wird als punktsymmetrisch bezeichnet, wenn ein Punkt existiert, an welchem diese Funktion in der Form gespiegelt werden kann, damit sie und ihr Spiegelbild kongruent sind. Liegt eine Punktsymmetrie vor, so gilt: f(-x) = -f(x). Dies bedeutet: Die Funktion ist symmetrisch zum Ursprung bzw. besitzt eine Symmetrie zum Ursprung.

Ist eine Funktion symmetrisch zu einem Punkt, so kann diese Funktion in dieser Weise in horizontaler und vertikaler Richtung verschoben werden, dass sich der Symmetriepunkt im Koordinatenursprung befindet.
 
Achsensymmetrische Funktion: Eine Funktion heißt achsensymmetrisch, wenn eine Gerade (bzw. Achse) existiert, an welcher diese Funktion in der Form gespiegelt werden kann, damit sie sowie ihr Spiegelbild kongruent sind. Liegt eine Achsensymmetrie zur y-Achse vor, so gilt: f(-x) =  f(x).

Ist eine Funktion symmetrisch zur y-Achse des Koordinatensystems, so kann diese Funktion in der Form in horizontaler Richtung verschoben werden, dass sich die Symmetrieachse auf der y-Achse befindet.
 
  

 

Abbildung 1

 

Abbildung 2

 

Um sich eine oder mehrere Funktionen, sowie Optionen dieser grafisch darstellen zu lassen, sollten Sie Folgendes ausführen:
 

1. Definieren Sie die zu analysierende Funktion in einem Eingabefeld gemäß den geltenden Syntaxregeln. Geben Sie bei Bedarf einen weiteren Funktionsterm im zweiten Feld ein und aktivieren Sie das/die entsprechende(n) Kontrollkästchen mit den Bezeichnungen f(x,p)= bzw. g(x,p)=.
    
2. Aktivieren Sie die entsprechenden Kontrollkästchen, deren funktionalen Zusammenhang Sie sich ausgeben lassen möchten.
   
   Die links angeordnete Gruppe mit Kontrollkästchen Darstellen von f(x,p) bezieht sich auf das obere Eingabefeld für f(x,p), die rechts angeordnete Gruppe Darstellen von g(x,p) auf das untere Eingabefeld g(x,p). Die darunter angeordnete Gruppe Darstellen von f(x,p) und g(x,p) auf beide Eingabefelder.
    
3. Wählen Sie bei Bedarf den Menübefehl Optionen - Koordinatenwertanalyse, um zusätzlich eine Koordinatenwertanalyse durchzuführen.
    
4. Bedienen Sie die Schaltfläche Darstellen.
    
5. Enthält einer der definierten Funktionsterme das Einzelzeichen P, so legen Sie, wie unter Verwendung von Funktionsparametern beschrieben, nach einer Bedienung des Schalters Parameter P den zu durchlaufenden Wertebereich für diesen Funktionsparameter, sowie die zu verwendende Schrittweite, fest. Positionieren Sie hierauf den Schieberegler Parameter P, um den Einfluss des Parameters P zu untersuchen.
   
   Um eine automatisch ablaufende Parameterwertsimulation durchführen zu lassen, klicken Sie auf die Schaltfläche Simulation. Beendet werden kann die Ausführung dieser wieder durch eine erneute Betätigung derselben Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.

Hinweise:

Bei der Definition einer parameterhaltigen Funktion ist die Darstellung von Stammfunktionen, sowie Evoluten nicht möglich. Eine Funktionsverknüpfung Darstellen von f(x,p) und g(x,p) wird nur ausgegeben, wenn sich in beiden Eingabefeldern eine gültige Funktionsdeklaration befindet, andernfalls wird die Ausgabe dieser ignoriert.
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

 
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im Mathe-Leistungskurs (LK).
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

https://www.redusoft.de/images/videos_help_mathprof/Analysis_Mathematische_Funktionen_II_4.mp4  

 

 

Enthält ein Funktionsterm der auszugebenden Kurven das Einzelzeichen P zur Definition eines Funktionsparameters, so wird bei der Ausgabe einer grafischen Darstellung nachfolgend gezeigtes Bedienformular zur Verfügung gestellt.
 

 

 

Wird der Menüeintrag Optionen - Koordinatenwertanalyse aktiviert, so kann eine Koordinatenwertanalyse durchgeführt werden. Hierbei erscheint ein Bedienformular, durch welches es bei Ausgabe der grafischen Darstellung ermöglicht wird, sich Koordinatenwerte der dargestellten Kurve(n) ausgeben zu lassen.

 

 

Es bestehen folgende Möglichkeiten Koordinatenwertanalysen durchführen zu lassen:
 

• Klicken Sie in einen rechteckig umrahmten Mausfangbereich der markierten Untersuchungsstelle und bewegen Sie den Mauscursor bei gedrückt gehaltener Maustaste nach links oder nach rechts.
   

• Bedienen Sie die Schaltfläche Punkt, geben Sie den entsprechenden Abszissen-Koordinatenwert ein und bestätigen Sie mit OK.
   

• Benutzen Sie den Schalter Simulation, um eine Koordinatenwertanalyse der Funktion über den gesamten Darstellungsbereich hinweg simulieren zu lassen.

  Beenden können Sie diese Simulation wieder, indem Sie den Schalter, welcher nun die Bezeichnung Sim. Stop. trägt, bedienen.

Hinweise:

Die Kontrollkästchen Linien und Koordinaten ermöglichen die Ein-/Ausblendung von Hilfslinien und Koordinatenwerten. Für Stammfunktionen und Evoluten wird keine Koordinatenwertanalyse durchgeführt.

 

Untersuchen Sie parameterhaltige Funktionen, so besteht nicht die Möglichkeit eine Koordinatenwertanalyse über den gesamten Darstellungsbereich hinweg simulieren zu lassen. In diesem Fall jedoch kann diese, wie zuvor beschrieben, per Mausbewegung oder mittels einer Bedienung der Schaltfläche Punkt durchgeführt werden.
 

Analytische Ermittlung von Ableitungen

 
Unter dem Menüpunkt Ableitung - Ableitung analytisch können Sie sich die 1. und 2. Ableitung einer Funktion symbolisch differenziert ausgeben lassen. Es erscheint ein Formular.

1. Definieren Sie den Funktionsterm, gemäß den geltenden Syntaxregeln, im Eingabefeld mit der Bezeichnung Y = f(x) =.
    
2. Nach der korrekten Deklaration der Funktion im Eingabefeld und der Bedienung des Schalters Ermitteln wird die 1. und 2. Ableitung der eingegebenen Funktion ermittelt und in den entsprechenden Ausgabefeldern angezeigt.

Ist die Funktionsdeklaration zu komplex, um eine Ableitung symbolisch differenzieren zu können, so erscheint der Eintrag 'Funktion zu komplex - nicht differenzierbar' in den Ausgabefeldern.

Durch einen Klick auf die dortige Schaltfläche Schließen kehren Sie wieder zum Unterprogramm zurück.

Hinweis:

Beinhaltet eine Funktionsdeklaration den Parameter P, so erhalten Sie eine Fehlermeldung, da parameterhaltige Funktionen nicht analytisch differenziert werden können.
 

 

Für Evoluten und Stammfunktionen wird keine Koordinatenwertanalyse durchgeführt.

 

Die Durchführung von Koordinatenwertanalysen ist bei Einstellung einer logarithmischen Skalierung bzgl. der Y-Achse bzw. der X- und Y-Achse nicht möglich. Wurde eine dieser vor Durchführung einer Koordinatenwertanalyse eingestellt, so schaltet das Programm nach erstmaligem Wiederaufruf automatisch auf die logarithmische Skalierung bzgl. der X-Achse bzw. nichtlineare Skalierung um.

 

Funktionen können Sie in diesem Unterprogramm auch definieren, bzw. aus der Funktionsbibliothek übernehmen, während sich das Programm im Darstellungsmodus befindet. Wählen Sie den Menüeintrag Datei / Funktionsterm(e) holen, so wird ein Formular geöffnet, auf welchem Sie dies durch einen Doppelklick auf den entsprechenden Eintrag (falls vorhanden) in der Tabelle, oder die Definition einer Funktion im dafür vorgesehenen Eingabefeld vornehmen können.

 

In diesem Modul steht ferner eine kleine Funktionsbibliothek zur Verfügung, die es ermöglicht, sich die geltenden Syntaxregeln zur Definition von Funktionstermen verständlich zu machen. Aufgerufen werden kann sie unter dem Menüpunkt Beispiele I - Beispiel - Funktionsbibliothek laden.

 

Eine Anleitung zur Durchführung von Kurvenpunktmarkierungen finden Sie unter Kurvenpunktmarkierung.

 

 

Mathematische Funktionen I

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 
Beispiel 1 - Graph ohne Funktionsparameter:

Um den Zusammenhang zu prüfen, wie sich die 1. Ableitung der Funktion y = f(x) = 3·sin(-cos(x/2)) verhält, definieren Sie den Term 3*SIN(-COS(X/2)) im oberen Eingabefeld und aktivieren die Kontrollkästchen f(x,p) =, Funktion f(x,p) und 1. Ableitung f'(x,p) auf der linken Seite.

Deaktivieren Sie alle anderen Kontrollkästchen im Auswahlformularbereich und bedienen Sie hierauf die Schaltfläche Darstellen. Der Funktionsgraph der entsprechenden Kurven wird hierauf wie nachfolgend gezeigt, ausgegeben:
 

 

Beispiel 2 - Graph mit Funktionsparameter:

Um die Kombinationen f(x,p) + g(x,p) sowie f(x,p) - g(x,p) der beiden Funktionsterme f(x,p) = 3·sin(p-cos(x/2)) und g(x) = x/2 zu untersuchen, löschen Sie die Einträge bereits beschriebener Eingabefelder.

 

Hierauf geben Sie den Term 3*SIN(P-COS(X/2)) in das Feld mit Bezeichnung f(x,p) = und den Term X/2 in das Feld mit Bezeichnung g(x,p) = ein.

 

Aktivieren Sie die Kontrollkästchen mit den Bezeichnungen f(x,p) =, Funktion f(x,p), f(x,p) + g(x,p), f(x,p) - g(x,p), deaktivieren Sie alle anderen Kontrollkästchen und bedienen Sie die Schaltfläche Darstellen.
  

 
Das Programm hat hierbei automatisch erkannt, dass es sich um parameterhaltige Funktionen handelt und stellt deshalb ein Bedienformular zur Parameterkonfiguration zur Verfügung.

 

Somit werden zunächst folgende Funktionen mit dem voreingestellten Parameterwert p = -5 dargestellt:

 

f(x,p) = 3·sin((-5)-cos(x/2))

f(x,p) + g(x,p) = 3·sin((-5)-cos(x/2))+(x/2)

f(x,p) - g(x,p) = 3·sin((-5)-cos(x/2))-(x/2)

 

Durch die Positionsveränderung des auf dem Bedienformular vorhandenen Schiebereglers Parameter P werden bei einem voreingestellten Parameterwertebereich von -5 ≤ p ≤; 5 und einer Parameterschrittweite von 0,1 nacheinander folgende Funktionen dargestellt:

 

f(x,p) = 3·sin((-4,9)-cos(x/2))

f(x,p) + g(x,p) = 3·sin((-4,9)-cos(x/2))+(x/2)

f(x,p) - g(x,p) = 3·sin((-4,9)-cos(x/2))-(x/2)

 

f(x,p) = 3·sin((-4,8)-COS(x/2))

f(x,p) + g(x,p) = 3·sin((-4,8)-cos(x/2))+(x/2)

f(x,p) - g(x,p) = 3·sin((-4,8)-cos(x/2))-(x/2)

 

f(x,p) = 3·sin((-4,7)-cos(x/2))

f(x,p) + g(x,p) = 3·sin((-4,7)-cos(x/2))+(x/2)

f(x,p) - g(x,p) = 3·sin((-4,7)-cos(x/2))-(x/2)

 

f(x,p) = 3·sin((-4,6)-cos(x/2))

f(x,p) + g(x,p) = 3·sin((-4,6)-cos(x/2))+(x/2)

f(x,p) - g(x,p) = 3·sin((-4,6)-cos(x/2))-(x/2)

.

.

.

usw.

 

Ändern können Sie diese Parametereinstellungen, indem Sie die Schaltfläche Parameter P anklicken. Eine Parameter-Autosimulation starten Sie durch die Bedienung der Schaltfläche Simulation.
 
 

Beispiel 3 - Koordinatenwertanalyse:

Gilt es, den Verlauf der 1. und 2. Ableitung einer Funktion y = f(x) = 3·cos(cos(x/2)-2·sin(x/2) mittels Koordinatenwertanalyse ermitteln zu lassen, so kann folgendermaßen vorgegangen werden:
 

 

 
 

Nach Löschung aller bisher definierten Funktionsterme wird der Ausdruck 3*COS(COS(X/2))-2*SIN(X/2) in das oberste Eingabefeld eingetragen. Aktivieren Sie die Kontrollkästchen mit den Bezeichnungen f(x,p) =, 1. Ableitung f'(x,p), 2. Ableitung f''(x,p) und deaktivieren Sie alle anderen.

 

Nach einer Aktivierung des Menüeintrags Optionen - Koordinatenwertanalyse und einem anschließenden Klick auf die Schaltfläche Darstellen werden die Funktionsgraphen der Kurven ausgegeben.

 

Durch Mauspositionierung (oder eine Bedienung der Schaltfläche Punkt und der Eingabe des gewünschten Werts in das linke Eingabefeld, mit anschließender Bestätigung durch Ok) werden die Koordinatenwerte an gewünschter Untersuchungsstelle ausgegeben.

 

Folgende Koordinatenwerte werden bei Stelle x = 7 angezeigt:

 

Funktionswert: y = f(7) = 0,07

Funktionswert der 1. Ableitung: y = f'(7) = 0,07

Funktionswert der 2. Ableitung: y = f''(7) = -0,245

 

Um sich die Funktionswerte der Ableitungen an jeder Stelle innerhalb des gesamten Darstellungsintervalls anzeigen zu lassen, bedienen Sie die Schaltfläche Simulation.
 
 

Beispiel 4 - Analytische Ableitung:

Es gilt, die 1. und 2. Ableitung der Funktion f(x) = cos(x)·sin(x-1) algebraisch, analytisch ermitteln zu lassen.

 

Nachdem Sie den Term COS(X)*SIN(X-1) im oberen Eingabefeld f(x,p) = definiert haben, den Menüeintrag Ableitung - Ableitung analytisch aktivierten und den Schalter Ermitteln bedient haben, werden folgende Ergebnisse in algebraischer Form ausgegeben:

 

1. Ableitung f'(x) = COS(X)*COS(X-1)-SIN(X)*SIN(X-1)

2. Ableitung f''(x) = -2*COS(X)*SIN(X-1)-2*COS(X-1)*SIN(X)
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3


Grafische Darstellung - Beispiel 4


Grafische Darstellung - Beispiel 5


Grafische Darstellung - Beispiel 6


Grafische Darstellung - Beispiel 7


Grafische Darstellung - Beispiel 8


Grafische Darstellung - Beispiel 9


Grafische Darstellung - Beispiel 10


Grafische Darstellung - Beispiel 11


Grafische Darstellung - Beispiel 12


Grafische Darstellung - Beispiel 13

      

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Funktionsgraph, Wikipedia - Gerade und ungerade Funktionen sowie unter Wikipedia - Mathematische Funktion zu finden.

 

 

 

Mathematische Funktionen I - Funktionen in Parameterform - Funktionen in Polarform - Segmentweise definierte Funktionen - Kurvenscharen - Funktionsparameteranalyse - Funktionswertetabellen - Iteration - Parameter der Sinus- und Cosinusfunktion - Parameter der Logarithmusfunktion - Parameter der Betragsfunktion - Parameter der Integer-Funktion - Parameter der Quadratwurzelfunktion - Parameter der Potenzfunktion - Parameter der Exponentialfunktion - Kubische Funktion in allgemeiner Form - Kubische Funktion in spezieller Form - Zahlenfolgen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Rekursive Zahlenfolgen - Interaktiv - Arithmetische und geometrische Zahlenfolgen - Parabelgleichungen - Parabelgleichungen - Interaktiv - Parabel und Gerade - Interaktiv - Analyse quadratischer Funktionen - Ermittlung ganzrationaler Funktionen - Ganzrationale Funktionen (Polynome) - Ganzrationale Funktionen (Polynome) - Interaktiv - Gebrochenrationale Funktionen - Gebrochenrationale Funktionen - Interaktiv - Interpolation nach Newton und Lagrange - Interpolation ganzrationaler Funktionen - Polynomregression - Nullstellen - Iterationsverfahren - Horner-Schema - Tangente - Normale - Tangente - Sekante - Tangente und Normale von externem Punkt - Kurvendiskussion - Kurvendiskussion - Interaktiv - Obersummen und Untersummen - Obersummen und Untersummen - Interaktiv - Integrationsmethoden - Rotationsparaboloid (3D) - Integralrechnung - Integralrechnung - Interaktiv - Zykloide - Hypozykloide - Epizykloide - Sternkurven - Zissoide - Strophoide - Kartesisches Blatt - Semikubische Parabel - Archimedische Spirale - Logarithmische Spirale - Fourier-Summen - Fourier-Reihen - Taylorreihen und Potenzreihen - Implizite Funktionen
 

 

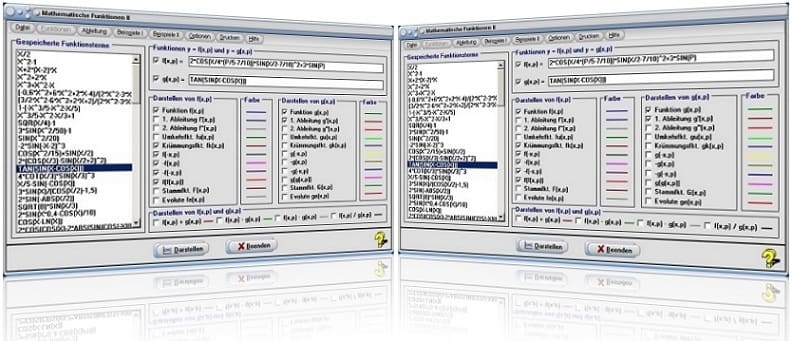
Startfenster des Unterprogramms Mathematische Funktionen II
 

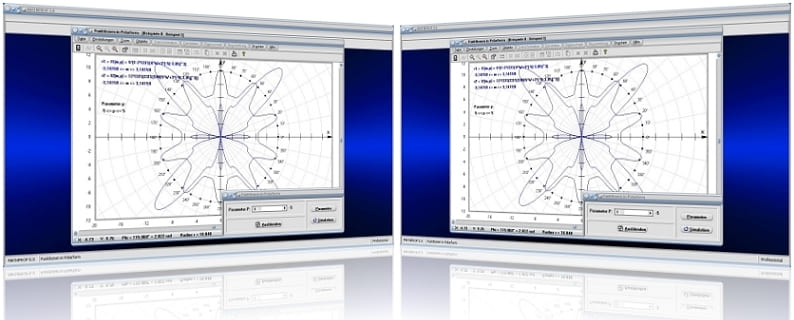
MathProf 5.0 - Unterprogramm Funktionen in Polarform

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---