MathProf - Mandelbrotmenge - Julia-Menge - Fraktale - Apfelmännchen

Fachthemen: Mandelbrotmenge und Juliamenge
MathProf - Software für interaktive Mathematik und fraktale Geometrie zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für Schüler, Abiturienten, Studenten, Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Programm zur Darstellung der Fraktale, welche als Juliamengen
und Mandelbrotmengen bzw. Mandelbrot-Fraktale bekannt sind.
Dieses Unterprogramm ermöglicht unter anderem die grafische Ausgabe des Apfelmännchens sowie anderer Mandelbrot-Sets, welche durch Festlegung entsprechender Parameter beeinflusst werden können. Auch der Zoom einer dargestellten Mandelbrotmenge ist möglich.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben, sind implementiert.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte zu diesem Modul:Mandelbrotmenge - Mandelbrot - Fraktale - Apfelmännchen - Julia-Menge - Juliamenge - Julia Menge - Mandelbrot-Set - Mandelbrot-Generator - Programm - Chaos - Chaostheorie - Chaotisches System - Fraktale erstellen - Fraktale zeichnen - Fraktalbilder - Grafisch - Fraktale in der Mathematik - Fraktale Geometrie - Fraktale Systeme - Animation - Plotten - Fraktale berechnen - Fraktale generieren - Geometrische Muster - Software - Kunst - Fraktalgenerator - Fraktal-Programm - Benoit Mandelbrot - Mandelbrot-Fraktale - Männchen - Mathematik - Mathe - Beispiel - Definition - Bild - Was ist - Welche - Welcher - Welches - Wodurch - Bedeutung - Was bedeutet - Erklärung - Einfach erklärt - Einführung - Beschreibung - Definition - Darstellen - Fraktal - Koordinaten - Menge - Grafik - Effekt - Iteration - Set - Erzeugen - Erstellen - Komplex - Generator - Mandelbrot-Zoom - Komplexe Zahlen - Formel - Rechner - Berechnen - Zeichnen - Funktionen - Eigenschaften - Graph - Theorie - Chaos-Theorie - Gleichung - Plotten - Iteration - Konstante - Viewer - Zoom - Bilder - Strukturen - Arbeitsblatt - Unterrichtsmaterial - Anwendungsaufgaben - Darstellung - Parameter - Plot - Darstellen - Plotter - Video - Software - Fraktalbilder |
Fraktale - Mandelbrotmenge - Juliamenge
Modul Mandelbrot- und Juliamengen
Das Unterprogramm [Sonstiges] - [Fraktale] - Mandelbrot- und Juliamengen ermöglicht die grafische Darstellung verschiedener Varianten von Julia- und Mandelbrotmengen (Apfelmännchen).

Fraktale sind mathematische Objekte, die selbstähnlich und chaotisch sind. Die meisten Fraktale, unter denen das sogenannte Apfelmännchen wahrscheinlich eines der bekanntesten ist, werden durch mathematische Gleichungen erzeugt. Die faszinierenden Bilder entstehen, indem Lösungen iterativer Prozesse unter Verwendung von Farbzuordnungen in einem Koordinatensystem dargestellt werden. Es sind sich selbst ähnliche Strukturen, die sich auf verschiedenen Abbildungsebenen immer wiederholen.
Es besteht ein enger Zusammenhang zwischen Fraktalen und dem physikalischen Begriff des sogenannten determinierten Chaos. Heute eröffnen Simulationsmethoden auf der Grundlage der Chaos-Theorie völlig neue Einblicke in das Weltbild der Wissenschaft und führen zu veränderten Denk- und Arbeitsmöglichkeiten.
In diesem Unterprogramm können mehr als 100 verschiedene Varianten von Fraktalen grafisch ausgegeben und analysiert werden. Zu den bekanntesten gehören die Juliamengen und Mandelbrotmengen, auf welche nachfolgend kurz eingegangen wird.
Mandelbrotmenge - Julia-Menge - Zusammenhänge
Die Mandelbrotmenge (benannt nach ihrem Entdecker Benoit Mandelbrot) ist eine Teilmenge der komplexen Ebene. Sie setzt sich aus aus komplexen Zahlen zusammen, die jeweils ein bestimmtes Kriterium erfüllen. Die x-Achse der zu erzeugenden Grafik entspricht dem Realteil einer komplexen Zahl und die y-Achse dem Imaginärteil derer.
Man durchläuft der Reihe nach viele Punkte innerhalb der komplexen Ebene und prüft, ob sie innerhalb der Mandelbrotmenge liegen. Es gibt somit vorerst nur zwei Arten von Punkten: die einen Punkte liegen nicht in der Menge und werden nicht gefärbt. Die anderen liegen innerhalb der Menge und erhalten zum Beispiel die Farbe Schwarz.
Wird ein Bildschirm als Ausschnitt aus einer Ebene aufgefasst und wird ein Punkt dieser Ebene mit den Koordinaten (x ,y) als komplexe Zahl z = x + iy behandelt, so können komplexe Zahlen als Punkte auf dem Bildschirm dargestellt werden. Eine Mandelbrotmenge entsteht, wenn die durch Iteration definierte Folge zn+1 = zn2 + c für komplexe c mit z0 = c untersucht wird und danach gefragt wird, ob sie konvergiert oder divergiert.
Der Zusammenhang lässt sich im komplexen Zahlenbereich beschreiben mit der Formel (Funktion):
f(zn) = xn-1² - yn-1² +cr + i· (2xn-1· yn-1 + ci)
unter Verwendung der komplexen Zahlen
z = x + iy
c = cr + ci
Die Iteration wird mit den Startwerten x = 0 und y = 0 begonnen. Wird diese entweder nach dem Erreichen einer festgelegten Anzahl durchzuführender Iterationen oder dem Überschreiten eines festgelegten Werts abgebrochen, so erhält man die Mandelbrotmenge (Apfelmännchen).
Der Abbruch erfolgt, wenn der Betrag von z größer ist als der festgelegte Grenzwert (|z| > Grenzwert).
Da es möglich ist einen Grenzwert dafür zu bilden, durch welchen bestimmt wird, ob die Iteration bei einem vorgegebenen Wert c konvergiert oder divergiert, wird sowohl ein Grenzwert, wie auch eine Zahl festgelegt, welche die Anzahl durchzuführender Iterationen bestimmt.
Das Vorliegen einer Divergenz wird angenommen, wenn der iterativ ermittelte Betrag der Größe z diesen Grenzwert einmalig überschreitet. Wird der Grenzwert hingegen während der Iteration nicht überschritten, so wird Konvergenz angenommen. Die eigentliche Mandelbrotmenge wird durch den mehrfarbig gefärbten Bereich dargestellt, für dessen Punkte die Iteration nicht divergiert.
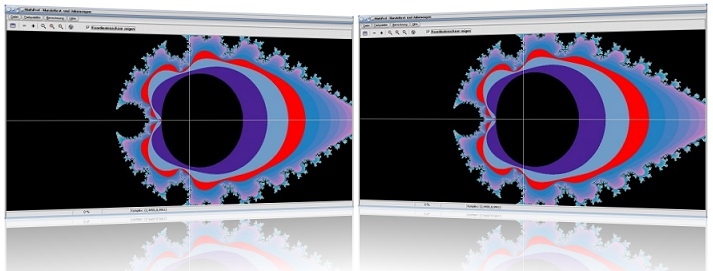
Vergrößerte Darstellung:

Bild 1 - Mandelbrotmenge ohne Vergrößerung

Bild 2 - Mandelbrotmenge mit Vergrößerung
Eine Mandelbrotmenge kann prinzipiell nach Belieben vergrößert werden. Es gilt jedoch darauf zu achten, dass die Anzahl der Iterationen hierbei entsprechend erhöht wird. Mittels dieser Erhöhung der Anzahl durchzuführender Iterationen können die Ränder der entsprechenden Mandelbrotmenge detaillierter untersucht werden.
Julia-Menge
Der französische Mathematiker Gaston Julia untersuchte bereits zu Anfang des 20. Jahrhunderts den oben aufgeführten Zusammenhang. Bei Mandelbrotmengen ist die komplexe Konstante c veränderlich und die entsprechenden Punktkoordinaten (Pixelfärbung) werden hierdurch ermittelt. Bei Juliamengen hingegen werden der reelle, wie auch der imaginäre Teil dieses Wertes konstant gehalten.
Als Julia-Menge sind die Punkte der Koordinatenebene definiert, für welche die Iteration den bestimmten Abbruchwert nicht überschreiten (konvergieren).
Bei einer Juliamenge werden z die Koordinaten eines beliebigen Punktes der komplexen Zahlenebene zugewiesen, während die Konstante c für alle Punkte beibehalten wird. Auch in diesem Fall handelt es sich bei c um einen komplexen Wert der in der komplexen Zahlenebene dargestellt werden kann. Dieser muss bei allen durchgeführten Berechnungen für die zukünftig auszugebenede Juliamenge denselben Wert besitzen und darf somit nicht verändert werden.
Da c beliebige Koordinatenwerte besitzen kann, ist jedem Punkt der komplexen Zahlenebene eine separate Juliamenge zugeordnet. Dies bedeutet, dass auch jedem Punkt der Mandelbrotmenge eine Juliamenge zugeordnet ist.
Darstellung
Um sich eine Mandelbrot- oder Juliamenge in diesem Programm darstellen zu lassen, sollten Sie Folgendes durchführen:
- Ist keine Auswahlliste eingeblendet, so wählen Sie den Menüpunkt Datei / Fraktalauswahl einblenden.
- Führen Sie einen Doppelklick auf einen Eintrag in der links zur Verfügung stehenden Auswahlliste aus. Erscheint daraufhin ein Fenster zur Eingabe formelspezifischer Parameter, so können Sie diese ggf. ändern. Nach einer Bedienung der Schaltfläche Übernehmen wird das Fraktal dargestellt.
Durch die Benutzung der Symbolschaltflächen - bzw. + können Sie die Anzahl durchzuführender Iterationen reduzieren bzw. erhöhen (deren Anzahl wird in der Statusleiste am unteren linken Bildschirmrand angezeigt).
Mit Hilfe der in der Symbolleiste zur Verfügung stehenden Lupensymbole kann der Darstellungsbereich vergrößert, verkleinert bzw. in den Urzustand zurückversetzt werden.
Möchten Sie den Ausgabebereich der Darstellung durch Mausbedienung vergrößern, so klicken Sie mit der linken Maustaste in den Darstellungsbereich des Fensters und ziehen unter Festhalten dieser Taste ein Rechteck auf (von links nach rechts und von oben nach unten). Nach dem Loslassen der Maustaste wird der umrandete Bereich auf den Gesamtdarstellungsbereich vergrößert. Um die Darstellung zu verkleinern, positionieren Sie den Mauszeiger innerhalb des Darstellungsbereichs und bedienen die rechte Maustaste. Der Koordinatenwertebereich der Darstellung wird um den Faktor 1:2 verkleinert.
Bei einer Verwendung des Menübefehls Berechnung - Berechnung / Starten bzw. Berechnung - Berechnung / Stoppen können Sie die Durchführung der Berechnung und somit die Aktualisierung der grafischen Darstellung veranlassen bzw. abbrechen.
Animation und Farbeinstellungen

Unter dem Menüpunkt Farbpalette kann eine Farbrotation initialisiert werden. Hierbei werden die 256 zur Darstellung des Fraktals verwendeten Farben bei einer Animation in kurzen Zeitabständen zyklisch vertauscht.
Durch eine Bedienung der Schaltfläche Mischen können Sie die zu verwendende Farbtauschfolge verändern. Bei einer Benutzung der Schaltflächen Nach links und Nach rechts können die beim Ablauf einer Animation zu durchlaufenen Farbtauschfolgen manuell ausgewählt werden. Diese Farbeinstellungen bleiben nach dem Schließen des Formulars erhalten.
Eine Benutzung der Schaltfläche Animation starten veranlasst das Programm, die gewählte Farbtauschfolge während der Darstellung unter Durchführung einer Simulation auszuführen.
Durch das Anklicken der Schaltfläche Ausblenden kann das Farbpalettenfenster während einer laufenden Simulation ausgeblendet werden. Eine Schaltfläche, die ein erneutes Einblenden des Farbpalettenfensters ermöglicht, erscheint daraufhin in der Symbolleiste.
Eine Animation können Sie wieder beenden, wenn Sie die auf dem Farbpalettenfenster zur Verfügung stehende Schaltfläche Beenden bedienen, oder im Menü des Hauptformulars den Eintrag Animation beenden wählen.
Hinweise
Die Berechnungszeit zur Darstellung von Fraktalen kann u.U. sehr zeitaufwendig sein. Möchten Sie die Aktualisierung einer Darstellung abbrechen, so können Sie hierfür den Menübefehl Berechnung / Berechnung stoppen wählen bzw. die Taste F3 oder die Taste ESC bedienen.
Einige Fraktale benötigen sog. formelspezifische Parameter. Hierbei handelt es sich um Real- bzw. Imaginärstartwerte für Konstanten. Diese können nach Aufruf eines Eintrags für die entsprechende Variante definiert werden. Zudem können zur Berechnung der Grenzwerte verschiedene Rundungsmethoden vorgegeben werden, welche Einfluss auf die Konvergenz bzw. Divergenz haben.
Benötigte Zahlenwerte können in den, nach getroffener Auswahl, erscheinenden Eingabefeldern festgelegt werden. Die bei der Berechnung zu verwendenden Rundungsmethoden können durch die Wahl eines Eintrags der zur Verfügung stehenden Auswahlboxen bestimmt werden.
Nach einer Bedienung der Schaltfläche Übernehmen werden die Berechnungen mit den vorgegebenen Parameterwerten durchgeführt und die Darstellung wird aktualisiert.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Allgemein
Möchten Sie die aktuelle Darstellung in die Zwischenablage kopieren, so können Sie den Befehl Datei / Darstellung in Zwischenablage kopieren verwenden. Das Bild steht somit zur Bearbeitung mit weiteren Anwendungen zur Verfügung.
Um ein Bild im Bitmap-Format abzuspeichern, verwenden Sie den Befehl Datei / Darstellung speichern.
Über den Menübefehl Datei / Beenden kehren Sie wieder zum Hauptformular des Programms zurück. Werden vom Programm keine Berechnungen durchgeführt, so bewirkt eine Benutzung der Taste ESC dasselbe.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet der Mathematik, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Weitere Themenbereiche
Zusammenhänge Mandelbrot-Juliamengen

Beispiel 1

Beispiel 2

Beispiel 3
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Mandelbrot-Menge sowie unter Wikipedia - Fraktal und unter Wikipedia - Benoit Mandelbrot zu finden.
Zahlenstrahl - Römische Zahlen - Schriftliche Addition - Schriftliche Subtraktion - Schriftliche Multiplikation - Schriftliche Division - Schriftliche Potenzierung - Aussagenlogik - Zahltypumwandlung - Zinsrechnung - Zinseszinsrechnung grafisch - Annuitätentilgung - Jahreszinsrechnung - Physikalische Größen - Materialkonstanten - Fachbegriffe Deutsch - Englisch - Zusammenhänge Mandelbrot-Juliamengen - Sierpinski-Dreieck - Koch-Kurve - Pythagoras-Baum - Feigenbaum-Diagramm - Lindenmayer-System - Lindenmayer-System II - Logistische Gleichung I - Logistische Gleichung II - Diagramme - Tortendiagramm - Kryptografie - Raumgittermodelle (3D) - Paare geordnet - Kalender - Rechnen mit selbstdefinierten Formeln - Zeichenprogramm - Tangram - Tetris - Spiel 15 - Türme von Hanoi - Dame - Schach
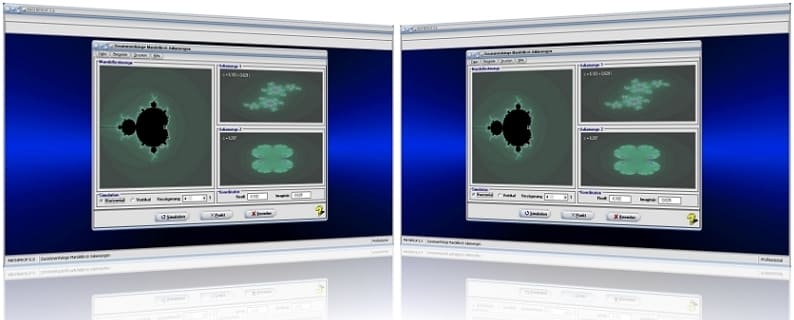
MathProf 5.0 - Unterprogramm Zusammenhänge bei Mandelbrot- und Juliamengen

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















