MathProf - Lotto - Lottomodell - Ziehung - Simulation

Fachthema: Lottoziehung - Simulation

MathProf - Stochastik - Statistik - Software für interaktive Mathematik für die Realschule, das Berufskolleg, das Gymnasium und das Studium zum Lösen verschiedenster Aufgaben sowie zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen.

Online-Hilfe
für das Modul zur Durchführung von simulativen Lotto-Ziehungen.

Ein Lotto-Zufallsgenerator erzeugt nach Festlegung eines Tipps entsprechende Ziehungen und gibt die ermittelte Anzahl von Treffern aus.

Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben, sind implementiert.

 

Weitere relevante Seiten zu diesem Programm

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

 

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Videoauswahl zu MathProf 5.0.
 

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche können Sie eine kostenlose Demoversion des Programms MathProf 5.0 herunterladen.

  

Themen und Stichworte zu diesem Modul: Lotto - Ziehung - Ziehungen - Zufallszahlen - Lottozahl - Lottozahlen - Zahlenlotto - Lottomodell - Zufällige Zahl - Zufällige Lottozahlen - Wahrscheinlichkeit - Glücksspiel - Zufallsgenerator - 6 aus 49 - Richtige - 3 Richtige - 4 Richtige - 5 Richtige - 6 Richtige - Zurücklegen - Zahlen - Wahrscheinlichkeitsrechner - Simulator - Generator - Simulation - System - Zahlenkombinationen - Beispiel - Algorithmus - Berechnung - Ergebnis - Erklärung - Einfach erklärt - Mathe - Mathematik - Bedeutung - Was bedeutet - Beschreibung - Rechner - Zufall - Berechnen - Reihenfolge - Lottoergebnisse - Lottotreffer - Lottoziehung - Lottoziehungen - Möglichkeiten - Kombinationen - Wahrscheinlichkeitsrechnung

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zum Inhaltsverzeichnis der in MathProf 5.0 implementierten Module bzw. zur Bestellseite für das Programm.
 

 

 

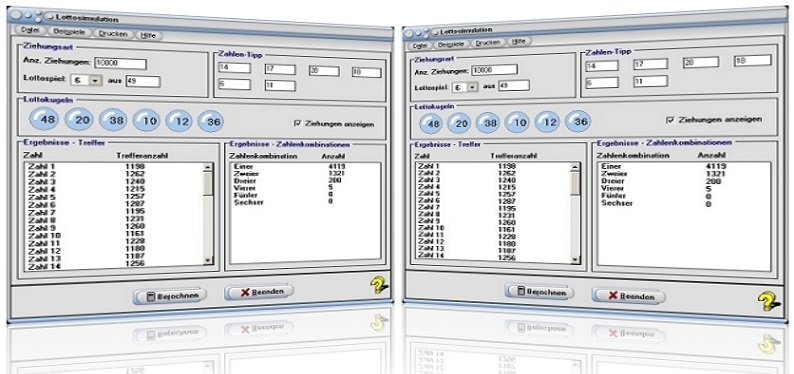
Modul Lottosimulation

 
Das Unterprogramm [Stochastik] - Lottosimulation ermöglicht die Durchführung von Lottosimulationen.

In diesem Modul zur Simulation von Lottoziehungen kann die Ziehung von einer bis zu acht, mit Zahlen beschrifteter Kugeln simuliert werden. Die Gesamtanzahl der zur Ziehung zur Verfügung stehenden Kugeln kann zwischen 4 und 99 betragen. Beim Aufruf des Unterprogramms ist eine Ziehung 6 aus 49 voreingestellt.
 
Das Programm führt diese Animation mit einem Zahlenlottto durch und ermittelt nach Abgabe eines Zahlentipps die Gesamtanzahl erzielter Treffer nach Durchführung einer festgelegten Anzahl von Simulationen und gibt diese in der linksseitig angeordneten Tabelle aus. Darüber hinaus wird die Anzahl richtig getippter Zahlen in der zweiten Tabelle gelistet.

Bei der Aufgabe die Wahrscheinlichkeit zu ermitteln, exakt k Richtige bei einer Ziehung "6 aus 49" zu erhalten, ist die hypergeometrische Verteilung zu verwenden. Hierbei ist von einer Grundgesamtheit aus N Elementen auszugehen, von welchen M eine bestimmte Eigenschaft (ein bestimmtes Merkmal) besitzen. Es werden n Elemente ohne Zurücklegen gezogen. X sei die Anzahl der Elemente der Stichprobe, welche die untersuchte Eigenschaft haben. Dann gilt die Wahrscheinlichkeitsfunktion:

Gehen Sie folgendermaßen vor, um eine Lottosimulation durchführen zu lassen:
 

1. Wählen Sie die Art des zu simulierenden Lottospiels durch die Bedienung der aufklappbaren Auswahlbox und der Eingabe eines entsprechenden Werts in das daneben angeordnete Feld.
    

2. Legen Sie die Anzahl durchzuführender Simulationen durch die Eingabe eines Werts in das Feld Anz. Ziehungen fest.
    

3. Geben Sie einen Tipp ab, indem Sie die Werte der entsprechenden Zahlen in die dafür vorgesehenen Felder (Zahlen-Tipp) eingeben.
    

4. Bedienen Sie die Schaltfläche Berechnen.

 
Bei Aktivierung des Kontrollkästchens Ziehungen anzeigen werden gezogene Lottokugeln angezeigt. Deren Darstellung benötigt viel Zeit. Wird es deaktiviert, so erfolgt die Auswertung wesentlich schneller.

Hinweis:

Das Programm führt die Simulation mit einem implementierten Zufallsgenerator aus. Da die Durchführung bei einer großen Anzahl von Ziehungen sehr zeitaufwändig sein kann, können Sie diese jederzeit durch einmaliges Drücken der Taste ESC abbrechen.

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

Hypergeometrische Verteilung

Hypergeometrische Verteilung - grafische Analyse

Beispiel 1:

Wie groß ist die Wahrscheinlichkeit, beim Lotto "6 aus 45" 4 Richtige zu tippen?

Es bestehen (6 über 4) Möglichkeiten, aus den 6 richtigen Zahlen 4 auszuwählen, sowie (39 über 2) Möglichkeiten, von den 39 falschen Zahlen 2 anzukreuzen. Insgesamt sind (45 über 6) verschiedene Tipps möglich. Somit beträgt die gesuchte Wahrscheinlichkeit:
 

Vorgehensweise und Lösung:

Legen Sie im Eingabefeld Anz. Ziehungen einen Wert von 100000 fest. Selektieren Sie aus der Auswahlbox Lottospiel die Zahl 6 und geben Sie in das rechts daneben angeordnete Feld die Zahl 45 ein.

Geben Sie durch die Eingabe sechs verschiedener Zahlenwerte im Formularbereich Zahlen-Tipp einen Tipp ab und bedienen Sie hierauf mehrmals die Schaltfläche Berechnen.

Das Programm simuliert die Anzahl festgelegter Ziehungen (100000) unter der Verwendung eines Zufallsgenerators. Es ist festzustellen, dass für die Anzahl Vierer stets ein Wert ermittelt wird, welcher sich mit o.a. Ergebnis deckt. (ca. 130 - 150 mal wird von 100000 Ziehungen die Zahl 4 gezogen ≈ 0,13-0,15%).

Wie groß ist die Wahrscheinlichkeit, beim Lotto "6 aus 49" 3 Richtige zu tippen?

Es bestehen (6 über 3) Möglichkeiten, aus den 6 richtigen Zahlen 3 auszuwählen, sowie (43 über 3) Möglichkeiten, von den 43 falschen Zahlen 3 anzukreuzen. Insgesamt sind (49 über 6) verschiedene Tipps möglich. Somit beträgt die gesuchte Wahrscheinlichkeit:
 

Beispiel 2:

Legen Sie im Eingabefeld Anz. Ziehungen einen Wert von 100000 fest. Selektieren Sie aus der Auswahlbox Lottospiel die Zahl 6 und geben Sie in das rechts daneben angeordnete Feld die Zahl 49 ein. Geben Sie durch die Eingabe sechs verschiedener Zahlenwerte im Formularbereich Zahlen-Tipp einen Tipp ab und bedienen Sie hierauf aufeinanderfolgend die mehrmals die Schaltfläche Berechnen um verschiedene Ergebnisse zu erhalten.

Das Programm simuliert die Anzahl festgelegter Ziehungen (100000) unter der Verwendung eines Zufallsgenerators. Es ist festzustellen, dass für die Anzahl Dreier stets ein Wert ermittelt wird, welcher sich mit o.a. Ergebnis deckt. (ca. 1700 - 1800 mal wird von 100000 Ziehungen ein Dreier gezogen ≈ 1,7-1,8%).
 

Beispiel 1


Beispiel 2

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Lotto zu finden. 
 

Kombinatorik - Urnenmodell - Pfadregel - Galton-Brett - Statistische Messwertanalyse - Hypothesentest - Binomialverteilung - Binomialverteilung - Interaktiv - Binomialkoeffizienten - Geometrische Verteilung - Geometrische Verteilung - Interaktiv - Poisson-Verteilung - Poisson-Verteilung - Interaktiv - Hypergeometrische Verteilung - Hypergeometrische Verteilung - Interaktiv - Stetige Verteilungen - Glockenkurve - Regressionsanalyse - Stichproben - Stichproben - Verteilungen - Vierfeldertest - Bedingte Wahrscheinlichkeit - Zusammenhang von Messwerten - Experimente - Gesetz der großen Zahlen - Berechnung von Pi (Monte-Carlo-Methode)

MathProf 5.0 - Unterprogramm Galton Brett

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

Unsere Produkte

 
Nachfolgend aufgeführt finden Sie Kurzinfos zu den von uns entwickelten Produkten.

 

I - MathProf 5.0
Mathematik interaktiv
 

MathProf 5.0 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich mathematische Sachverhalte auf einfache Weise zu verdeutlichen. Zudem spricht es diejenigen an, die sich für Mathematik interessieren, oder mathematische Probleme verschiedenster Art zu lösen haben und von grafischen 2D- und 3D-Echtzeitdarstellungen sowie Animationen beeindruckt sind.
 

 

Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.

Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
 

Kurzinfos zu Inhalten einiger Unterprogramme erhalten Sie unter:
 

• Kurzinfos zum Themengebiet Analysis
• Kurzinfos zum Themengebiet Geometrie
• Kurzinfos zum Themengebiet Algebra
• Kurzinfos zum Themengebiet 3D-Mathematik
• Kurzinfos zum Themengebiet Stochastik
• Kurzinfos zum Themengebiet Vektoralgebra
• Kurzinfos zum Themengebiet Trigonometrie
• Kurzinfos zu sonstigen Themengebieten

---

 

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Analysis eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Vektoralgebra eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in MathProf implementierten Modulen finden Sie, indem Sie den Reiter MathProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
 

 
 

 

 

II - PhysProf 1.1
Physik interaktiv
 

PhysProf 1.1 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich physikalische Gesetzmäßigkeiten und Gegebenheiten zu verdeutlichen. Es spricht alle an, die sich für die Ergründung physikalischer Prozessabläufe und derartige Zusammenhänge interessieren. In zahlreichen Unterprogrammen besteht die Möglichkeit, Veränderungen von Einflussgrößen manuell, oder durch die Ausgabe automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren. Inhaltlich umfasst es ca. 70 verschiedene Unterprogramme zu den Fachthemenbereichen Mechanik, Elektrotechnik, Thermodynamik und Optik.
 

 

Durch die Benutzung dieses Programms wird es ermöglicht, bereits bekannte Fachthemeninhalte aufzuarbeiten und entsprechende Sachverhalte numerisch wie auch grafisch zu analysieren. Mittels der freien Veränderbarkeit der Parameter von Einflussgrößen bei der Ausgabe grafischer Darstellungen besteht in vielen Unterprogrammen die Möglichkeit, Veränderungen an dargestellten Zusammenhängen manuell oder durch die Anwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
 

Eine Übersicht aller in PhysProf 1.1 zur Verfügung stehender Programmteile finden Sie im PhysProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

 

Kurzinfos zu Inhalten einiger Unterprogramme von Physprof 1.1 erhalten Sie unter:
 

• Kurzinfos zum Themengebiet Mechanik
• Kurzinfos zum Themengebiet Elektrotechnik
• Kurzinfos zum Themengebiet Optik
• Kurzinfos zum Themengebiet Thermodynamik
• Kurzinfos zu sonstigen Themengebieten

---

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in PhysProf implementierten Modulen finden Sie, indem Sie den Reiter PhysProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
 

 
 

 

 
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
 

SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.

Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.

 

 
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.

Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
 

Eine Inhaltsübersicht dessen finden Sie unter SimPlot - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

 

Beispiele einiger mit Simplot 1.0 erzeugter Grafiken finden Sie unter Beispiele, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

---

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.