MathProf - Lineare Optimierung - Simplex-Methode - Problem
Fachthema: Simplex-Methode
MathProf - Ein guter Begleiter zur Vorbereitung auf das Studium, zum Lösen verschiedenster mathematischer Probleme und zur Visualisierung relevanter Sachverhalte mittels Simulationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.
Online-Hilfe
für das Modul zur Anwendung der Simplex-Methode
zum Lösen von Aufgaben bzgl. der linearen Optimierung
mit Hilfe des Simplex-Algorithmus bei Definition einer Zielfunktion sowie der Festlegung von Nebenbedingungen.
Bei der in diesem Unterprogramm eingebundenen Methode handelt es sich um ein Optimierungsverfahren zur Lösung linearer Optimierungsprobleme, bei welcher relevante Nebenbedingungen in Form linearer Ungleichungen aufzustellen sind.
Das Programm ermittelt beim Berechnen der Lösungen derartiger Aufgaben die Koeffizienten einer linearen Zielfunktion, sowie deren Maximum bzw. Minimum.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben und dazu dienlich sind, Aufgaben zu diesem Themengebiet zu lösen, sind implementiert.
Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.
Themen und Stichworte zu diesem Modul:Simplex-Verfahren - Simplex-Algorithmus - Simplex-Methode - Simplexverfahren - Simplexmethode - Primaler Simplex - Programm - Maximierung - Wirtschaftsmathematik - Minimierung - Minimum - Maximum - Bedingungen - Koeffizienten - Optimierungsverfahren - Kosten - Kostenrechnung - Kostenminimierung - Optimierung - Optimierungsaufgaben - Optimierungsmethode - Gewinnmaximum - Gewinnmaximierung - Extremalprobleme - Optimierungsprobleme - Optimierungsrechner - Optimierungsrechnung - Nichtbasisvariable - Basislösung - Nebenbedingungen - Lineares Optimierungsproblem - Restriktionen - Simplex Tableau - Simplextableau - Schlupfvariablen - Nullvariablen - Basisvariablen - Lösen von Optimierungsaufgaben - Lösen von Maximierungsaufgaben - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Zielfunktion - Minimierungsproblem - Maximierungsproblem - Maximierungsfunktion - Gewinnmaximierung - Lösungen - Lineares Optimieren - Erklärung - Beschreibung - Definition - Ungleichungen - Simplex - Lineares Optimierungsmodell - Rechnerisch - Lösen - Lösung - Verfahren - Rechner - Berechnen - Bestimmen - Lineare Ungleichungssysteme berechnen |
Lineare Optimierung - Simplex Mehode
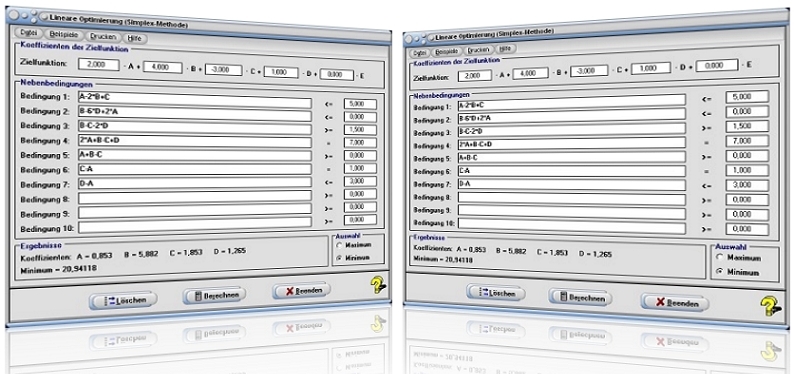
Modul Simplex-Methode
Das Unterprogramm [Algebra] - [Lineare Optimierung] - Lineare Optimierung - Simplex-Methode ermöglicht die Lösung von Optimierungsaufgaben mit Hilfe der Simplex-Methode.
Mit linearer Optimierung wird ein Teilgebiet der wirtschaftsmathematischen Optimierungsrechnung bezeichnet. Sie wird verwendet, um das Minimum beziehungsweise das Maximum einer linearen Funktion unter einschränkenden Bedingungen zu ermitteln. Der Simplex-Algorithmus ist ein Iterartionsverfahren mit zwei oder mehreren Variablen, welches zur Annäherung an ein Optimum verwendet wird.
Dieses Modul ermöglicht die Lösung derartiger Aufgaben mit Zielfunktionen, welche bis zu 5 Koeffizienten besitzen darf und eine Festlegung von maximal 10 Nebenbedingungen (Restriktionen).
Berechnung
Führen Sie Folgendes durch, um eine derartige Optimierungsaufgabe lösen zu lassen:
- Geben Sie die Koeffizienten der Zielfunktion in die Felder unter Koeffizienten der Zielfunktion ein.
- Definieren Sie die geltenden Nebenbedingungen (Restriktionen) in den dafür zur Verfügung stehenden Feldern Bedingung 1 - 10 (geben Sie den zugehörigen Zahlenwert in das zugehörige, rechts angeordnete Feld ein).
- Klicken Sie einmalig mit der linken Maustaste auf das entsprechende Symbol <=, = bzw. >= um die Art der Bedingung festzulegen.
- Wählen Sie durch die Aktivierung des Kontrollschalters Maximum bzw. Minimum, ob ein Maximum oder ein Minimum bestimmt werden soll.
- Bedienen Sie die Schaltfläche Berechnen.
Um alle Eingaben zu löschen, verwenden Sie die Schaltfläche Löschen.
Hinweise:
Beachten Sie, dass die Festlegung der Bedingungen lückenlos von oben nach unten erfolgen muss. Dies bedeutet, dass sich zwischen zwei erstellten Bedingungen kein leerbleibendes Eingabefeld zur Festlegung dieser befinden darf.
Es gilt auch darauf zu achten, dass sich festgelegte Nebenbedingungen nicht widersprechen. Ist dies dennoch der Fall, so gibt das Programm das Ergebnis Keine Lösung aus. Ebensolches gilt, wenn die Optimierung aufgrund einer fehlerhaften Bedingungsdeklaration nicht durchgeführt werden kann.
Zur Definition von Bedingungsdeklarationen dürfen die Zeichen A, B, C, D, E, numerische Zahlenwerte (nur mit nachfolgendem A, B, C, D oder E bzw. *) sowie die Zeichen +, - und * verwendet werden. Andere Zeichen sind nicht zugelassen.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Weitere Themenbereiche
Lineare Optimierung - Grafische Methode
Beispiel
Einem Betrieb stehen zur Herstellung zweier unterschiedlicher Textilien A und B drei verschiedene Rohstoffe: Schafwolle, Baumwolle, und Kunstfaser in den Mengen 550, 280 und 150 Einheiten zur Verfügung.
Zur Herstellung einer Längeneinheit von Textilie A werden von Schafwolle 3 und von Baumwolle 2 Einheiten benötigt. Für Textilie B werden 8 Einheiten von Schafwolle, 1 Einheit von Baumwolle und 3 Einheiten von Kunstfaser benötigt.
Beim Verkauf einer Längeneinheit von Textilie A erzielt man einen Deckungsbeitrag von 30 Geldeinheiten, bei Textilie B 50 Geldeinheiten. Wie viele Längeneinheiten sind von den einzelnen Textilien zu erzeugen und zu verkaufen, um maximalen Gewinn zu erzielen?
Nach Aufstellen der Zielfunktion mit:
Z = 30a + 50b = Maximum
und der Eingabe der Funktionskoeffizienten sowie der Deklaration der Nebenbedingungen in den Eingabefeldern mit:
Bedingung 1: 3a + 8a ≤ 550
Bedingung 2: 2a + b ≤ 280
Bedingung 3: 3b ≤ 150
ermittelt das Programm nach einer Aktivierung der Kontrollschalters Maximum und der Durchführung der notwendigen Berechnungen die Ergebnisse:
a = 130
b = 20
Maximum Z = 4900
Es wären somit von Textilie A 130 Längeneinheiten und von Textilie B 20 Längeneinheiten zu erzeugen um einen maximalen Gewinn von 4900 Geldeinheiten zu erzielen.
Wären zudem noch Fixkosten in Höhe von 1200 Geldeinheiten abzudecken, würde die Zielfunktion lauten:
Z = 30a + 50b - 1200 = Maximum
Nach Verwendung der gleichen Zielfunktion, der Aufstellung derselben Nebenbedingungen wie zuvor und anschließendem Abziehen des Fixkostenbetrags von 1200 Geldeinheiten wäre ein maximaler Gewinn von 3700 Geldeinheiten zu erzielen.
Beispiel 1
Beispiel 2
Beispiel 3
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Grafikprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Üben sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Übungen hierzu. Oftmals lassen sich hiermit auch die Lösungen von Übungsaufgaben durch benutzerdefinierte Festlegungen und Eingaben numerisch oder grafisch ermitteln bzw. auswerten. Erlernte Fertigkeiten können somit auf einfache Weise untersucht werden. Implementierte Beispiele zu Sachverhalten erlauben die Bezugnahme zum entsprechenden Fachthema.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Simplex-Verfahren sowie unter Wikipedia - Lineare Optimierung zu finden.
Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte
MathProf 5.0 - Unterprogramm Lineare Optimierung
MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.
Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.
Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
- Kurzinfos zum Themengebiet Analysis
- Kurzinfos zum Themengebiet Geometrie
- Kurzinfos zum Themengebiet Algebra
- Kurzinfos zum Themengebiet 3D-Mathematik
- Kurzinfos zum Themengebiet Stochastik
- Kurzinfos zum Themengebiet Vektoralgebra
- Kurzinfos zum Themengebiet Trigonometrie
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Physik interaktiv
Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
- Kurzinfos zum Themengebiet Mechanik
- Kurzinfos zum Themengebiet Elektrotechnik
- Kurzinfos zum Themengebiet Optik
- Kurzinfos zum Themengebiet Thermodynamik
- Kurzinfos zu sonstigen Themengebieten
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.
Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.
Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
