MathProf - Lindenmayer-System II (Fraktale)
Online-Hilfe für das Modul
zur Darstellung von Fraktalen
des Lindenmayer - Systems II
(Axiome und Regeln)
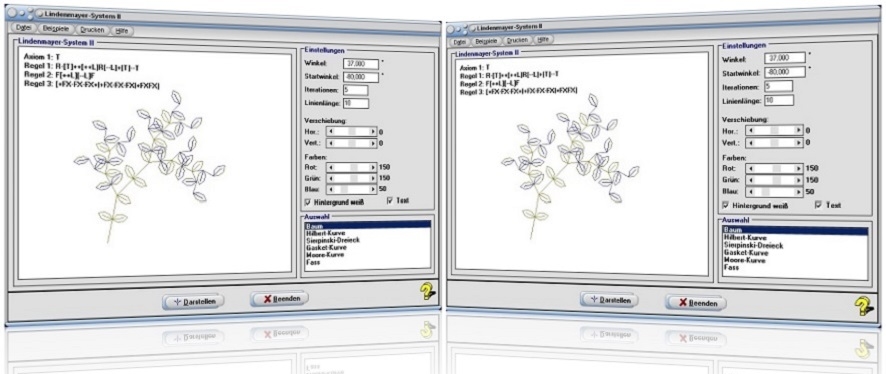
Lindenmayer-System II
Das Unterprogramm [Sonstiges] - Lindenmayer-System II ermöglicht die Untersuchung von Zusammenhängen bei der Darstellung von Fraktalen des erweiterten Lindenmayer-Systems II.
Einführende Hinweise zum Thema Lindenmayer-System finden Sie unter Lindenmayer-System.
Die Definition eines Fraktals mit Hilfe eines Lindenmayer-Systems kann auch über mehrere Schritte hinweg erfolgen. Hierzu wird zunächst ein Axiom als Startelement definiert und es werden Ersetzungsregeln festgelegt, die bestimmen, welche der verwendeten Symbolzeichen bei Durchlaufen eines nächsten Schritts durch komplexere Ausdrücke zu ersetzen sind.
Die Ordnung bestimmt die Anzahl der Ersetzungsvorgänge.
Axiom: F → R
Regel: R → F+F--F+F
Ordnung:
0: F
1: F+F--F+F
2: F+F--F+F+F+F--F+F--F+F--F+F+F+F--F+F
3: ...
Bei der Durchführung jeden Schritts (0 - n) wird Zeichen F durch die Zeichenfolge F+F--F+F ersetzt. Andere Zeichen bleiben unverändert.
In diesem kleinen Unterprogramm sind einige Beispiele implementiert, an welchen sich dieses Prinzip veranschaulichen lässt.
Der Startwinkel ist der Winkel, den die erste Strecke bezüglich der Horizontale besitzt. Dieser wird im Eingabefeld Startwinkel festgelegt. Im Eingabefeld Winkel definieren Sie den Winkel (im Gradmaß), der bei Durchführung einer Drehung zu verwenden ist. Bei Festlegung der Anzahl durchzuführender Iterationen, die im Eingabefeld Iterationen definiert wird, gilt es zu beachten, dass diese entscheidenden Einfluss auf die Dauer der Berechnungs- bzw. Darstellungszeit ausübt. Die Länge einzelner darzustellender Linien legen Sie durch die Eingabe eines ganzzahligen Werts in das Feld Linienlänge fest.
Darstellung
Führen Sie Folgendes aus, um sich Fraktale des Lindenmayer-Systems II darstellen zu lassen:
-
Wählen Sie die Art des darzustellenden Fraktals durch die Fokussierung des entsprechenden Eintrags in der Tabelle.
-
Legen Sie die Werte für Winkel, Startwinkel, die Anzahl durchzuführender Iterationen und der zu verwendenden Linienlänge in den dafür vorgesehenen Eingabefeldern fest.
-
Benutzen Sie die Rollbalken Hor. und Vert. um die Lage der Darstellung zu positionieren.
-
Um Farbwerte der Linien der Folge einzustellen, bewegen Sie die drei auf dem Bedienformular zur Verfügung stehenden Schieberegler Rot, Grün, Blau zur Einstellung der RGB-Werte.
-
Bedienen Sie die Schaltfläche Darstellen.
Sollen verwendete Axiome und Regeln innerhalb des Darstellungsbereichs ausgegeben werden, so aktivieren Sie das Kontrollkästchen Text. Möchten Sie, dass die Darstellung des Lindenmayer-Systems auf weißem Hintergrund ausgegeben wird, so aktivieren Sie das Kontrollkästchen Hintergrund weiß.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Weitere Themenbereiche
Zahlenstrahl - Römische Zahlen - Schriftliche Addition - Schriftliche Subtraktion - Schriftliche Multiplikation - Schriftliche Division - Schriftliche Potenzierung - Aussagenlogik - Zahltypumwandlung - Zinsrechnung - Zinseszinsrechnung grafisch - Annuitätentilgung - Jahreszinsrechnung - Physikalische Größen - Materialkonstanten - Fachbegriffe Deutsch - Englisch - Mandelbrot- und Juliamengen - Zusammenhänge Mandelbrot-Juliamengen - Sierpinski-Dreieck - Koch-Kurve - Pythagoras-Baum - Feigenbaum-Diagramm - Lindenmayer-System - Lindenmayer-System II - Logistische Gleichung I - Logistische Gleichung II - Diagramme - Tortendiagramm - Kryptografie - Raumgittermodelle (3D) - Paare geordnet - Kalender - Rechnen mit selbstdefinierten Formeln - Zeichenprogramm - Tangram - Tetris - Spiel 15 - Türme von Hanoi - Dame - Schach