MathProf - Langzahlarithmetik - Rechner - Große Zahlen - Lange Zahlen

Fachthemen: Lange Zahlen - Große Zahlen - Mod - Modulo

MathProf - Algebra - Software für interaktive Mathematik zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte mittels Simulationen, 2D- und 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Durchführung verschiedener mathematischer
Operationen und Berechnungen mit Zahlen übergroßer Ziffernlänge.

Bei diesem Unterprogramm handelt sich um einen Taschenrechner für lange Zahlen bzw. einen Rechner für große Zahlen. Er ermöglicht das Berechnen dieser unter Verwendung der Langzahlarithmetik. Zudem kann er bei Anwendung der Division als Modulo-Rechner eingesetzt werden.

Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben, sind implementiert.

 

Weitere relevante Seiten zu diesem Programm

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

 

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Videoauswahl zu MathProf 5.0.
 

 

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche können Sie eine kostenlose Demoversion des Programms MathProf 5.0 herunterladen.

 

Themen und Stichworte zu diesem Modul: Große Zahlen - Lange Zahlen - Sehr große Zahlen - Fakultät - Modulo - Mod - Berechnen - Rechner - Addieren - Subtrahieren - Multiplizieren - Dividieren - Quadrieren - Langzahlarithmetik - Geteilt - Halbieren - Erklärung - Beschreibung - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Herleitung - Beweis - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Klassenarbeit - Klassenarbeiten - Mathe - Mathematik - Anwendungsaufgaben - Mod-Rechner - Fakultät großer Zahlen - Berechnung - Multiplikation - Addition - Division - Subtraktion - Mal - Minus - Geteilt - Funktion - Operator - Operation - Arithmetik - Ergebnis - Einführung - Definition - Darstellen - Exponent - Teilen - Quadrat - Summe - Modulo-Rechner - Begriff - Begriffe - Rechnen - Divisor - ggT - kgV - Rest - Beispiel - 0 - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - Modulo 2 - Modulo 3 - Modulo 4 - Modulo 5 - Modulo 6 - Modulo 7 - Modulo 8 - Modulo 9 - Modulo 10 - Modulo 11 - Modulo rechnen - Rechnen mit langen Zahlen - Rechnen mit großen Zahlen

  

Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zum Inhaltsverzeichnis der in MathProf 5.0 implementierten Module bzw. zur Bestellseite für das Programm.
 

  

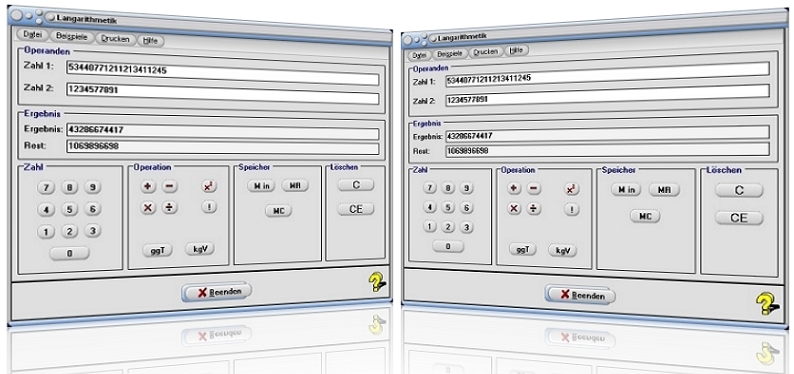
Modul Langarithmetik

Da es mitunter notwendig ist, Berechnungen mit Zahlen übergroßer Ziffernlänge durchzuführen, steht das kleine Unterprogramm [Algebra] - [Rechner] - Langarithmetik zur Verfügung.

Die Langzahlarithmetik behandelt das Rechnen mit Zahlen, bei denen sehr hohe Anzahlen an Stellen zu verarbeiten sind.

Große Zahlen (lange Zahlen) sind Zahlen, die wesentlich größer (länger) sind als die gewöhnlich verwendeten. Dieses Modul ermöglicht das Addieren, Subtrahieren, Multiplizieren, Dividieren und das Quadrieren von ganzen großen Zahlen. Neben der Durchführung der Addition, der Subtraktion, der Multiplikation oder der Division großer Zahlen, kann die Fakultät derartiger Zahlen berechnet werden.

Bei Modulo (kurz: mod) handelt es sich um eine mathematische Funktion bzw. eine Rechenoperation, die den Rest einer Division zweier ganzer Zahlen berechnet. Dieses Unterprogramm bietet die Möglichkeit auch dies durchführen zu lassen.

Folgende Möglichkeiten stehen in diesem Unterprogramm zur Auswahl, um Operationen mit langen Zahlen ausführen zu lassen:
 

• Addition
• Subtraktion
• Multiplikation
• Division (Mod-Rechner) 
• Ermittlung des größten gemeinsamen Teilers zweier Zahlen (ggT)
• Ermittlung des kleinsten gemeinsamen Vielfachen zweier Zahlen (kgV)
• Quadration einer Langzahl
• Fakultätsberechnungen mit Langzahlen (bis max. 999)

Um Berechnungen durchzuführen, geben Sie Zahlen in die Felder Zahl 1 bzw. Zahl 2 ein und bedienen hierauf die entsprechende Schaltfläche im Formularbereich Operation.

Hinweise:

Zur Bildung des Quadrats einer Langzahl muss die entsprechende Zahl im oberen Eingabefeld deklariert werden (Einträge im unteren Eingabefeld werden ignoriert). Die Berechnung der Fakultät einer Langzahl wird nur mit Zahlen durchgeführt die sich im oberen Eingabefeld befinden.

Im gesamten nachfolgend aufgeführten Text ist das Zeichen / als Symbolzeichen für Division zu interpretieren. Auf der Symbolschaltfläche im Unterprogramm wird ein synonymes Divisionssymbol hierfür verwendet.

Durch eine Bedienung der Taste CE können zuletzt gemachte Eingaben gelöscht werden.

Kann aufgrund mathematischer Fehler (z.B. Division durch 0) eine Rechenoperation nicht korrekt, oder vollständig ausgeführt werden, so erhalten Sie eine entsprechende Meldung. Durch die Bedienung der Taste C können Sie daraufhin in solch einem Fall wieder weiterarbeiten.

Bei zwei Zahlen a (Dividend) und b (Divisor) stellt modulo (bzw. mod) den Rest dar, der bei der Divison von a geteilt durch b entsteht.
 

Beispiel 1:

Gilt es, die Langzahlen 53440771211213411245 und 1234577891 dividieren zu lassen, so geben Sie die Zeichenfolge 53440771211213411245 in das Feld Zahl 1, die Zeichenfolge 1234577891 in das Feld Zahl 2 ein und bedienen die Schaltfläche /. Das Programm gibt hierauf folgendes Ergebnis aus:

53440771211213411245 / 1234577891 = 43286674417 Rest 1069896698 bzw. 43286674417 mod 1069896698

Beispiel 2:

Um sich das kleinste gemeinsame Vielfache dieser beiden Zahlen ausgeben zu lassen, klicken Sie auf den Schalter kgV. Das Programm ermittelt hierfür die Zahl: 65976794615353368805767784295

Beispiel 3:

Es gilt die Fakultät der Zahl 45 ermitteln zu lassen. Nach Festlegung dieser Zahl im oberen Eingabefeld und der Bedienung des Schalters ! gibt das Programm für diese Zahl aus:

1196222208654801945619631614956577150643837337
60000000000

Beispiel 4:

Es gilt die Fakultät der Zahl 101 ermitteln zu lassen. Nach Festlegung dieser Zahl im oberen Eingabefeld und der Bedienung des Schalters ! gibt das Programm für diese Zahl aus:

9425947759838359420851623124482936749562312794
7025437683278893534169775993162214765030878615
9180834691162349000354959958336970630260326400
0000000000000000000000

Beispiel 4:

Es gilt die Addition zweier langer Zahlen durchführen zu lassen. Nach Eingabe der Zahlen 53440771211213411245 und
1234577891 ermittelt das Programm nach einer Bedienung der Schaltfläche + das Ergebnis: 53440771212447989136

Beispiel 5:

Es gilt die Subtraktion zweier langer Zahlen durchführen zu lassen. Nach Eingabe der Zahlen 780000771211213411245 und
5670054444232 ermittelt das Programm nach einer Bedienung der Schaltfläche - das Ergebnis: 780000765541158967013

Beispiel 6:

Es gilt die Multiplikation zweier langer Zahlen durchführen zu lassen. Nach Eingabe der Zahlen 6789233445445667900088 und
33092787719999 ermittelt das Programm nach einer Bedienung der Schaltfläche * das Ergebnis: 224674661191650899377784907651459912

Beispiel 7:

Es gilt das kgV zweier langer Zahlen ermitteln zu lassen. Nach Eingabe der Zahlen 55550666008800756007 und
33092200066 ermittelt das Programm nach einer Bedienung der Schaltfläche kgV das Ergebnis: 1838293753362780334515695296462

Beispiel 8:

Es gilt den ggT zweier langer Zahlen ermitteln zu lassen. Nach Eingabe der Zahlen 96008800756806 und
555555555 ermittelt das Programm nach einer Bedienung der Schaltfläche ggT das Ergebnis: 9

Beispiel 8:

Es gilt den Modulo-2-Wert zweier Zahlen ermitteln zu lassen. Nach Eingabe der Zahlen 156797 und
2 ermittelt das Programm nach einer Bedienung der Schaltfläche / das Ergebnis: 78398 mod 1

Beispiel 8:

Es gilt den Modulo-3-Wert zweier Zahlen ermitteln zu lassen. Nach Eingabe der Zahlen 479017397 und
3 ermittelt das Programm nach einer Bedienung der Schaltfläche / das Ergebnis: 159672465 mod 2

Beispiel 9:

Es gilt den Modulo-4-Wert zweier Zahlen ermitteln zu lassen. Nach Eingabe der Zahlen 479017397 und
4 ermittelt das Programm nach einer Bedienung der Schaltfläche / das Ergebnis: 119754349 mod 1

Beispiel 10:

Es gilt den Modulo-5-Wert zweier Zahlen ermitteln zu lassen. Nach Eingabe der Zahlen 809017397099 und
5 ermittelt das Programm nach einer Bedienung der Schaltfläche / das Ergebnis: 161803479419 mod 4
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Mathe-Anwendungsaufgaben genutzt werden.
 
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
  

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 Beispiel 1


Beispiel 2

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
    

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Langarithmetik zu finden.

Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte

MathProf 5.0 - Unterprogramm Taschenrechner

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

Unsere Produkte

 
Nachfolgend aufgeführt finden Sie Kurzinfos zu den von uns entwickelten Produkten.

 

I - MathProf 5.0
Mathematik interaktiv
 

MathProf 5.0 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich mathematische Sachverhalte auf einfache Weise zu verdeutlichen. Zudem spricht es diejenigen an, die sich für Mathematik interessieren, oder mathematische Probleme verschiedenster Art zu lösen haben und von grafischen 2D- und 3D-Echtzeitdarstellungen sowie Animationen beeindruckt sind.
 

 

Es eignet sich insbesondere dafür, um interaktive grafische Untersuchungen sowie numerische Berechnungen zu entsprechenden Fachthemen durchführen zu lassen. Mehr als 300 verschiedene Unterprogramme decken die mathematischen Themenbereiche Analysis, Geometrie, Trigonometrie, Algebra, Stochastik, 3D-Mathematik und Vektoralgebra großflächig ab.

Durch die Nutzbarkeit vieler implementierter grafischer Features bestehen vielseitige gestaltungstechnische Möglichkeiten, ausgegebene Grafiken in entsprechenden Unterprogrammen auf individuelle Anforderungen anzupassen. Durch die freie Veränderbarkeit von Parametern und Koordinatenwerten bei der Ausgabe grafischer Darstellungen, besteht in vielen Modulen zudem die Möglichkeit, Veränderungen an dargestellten Gebilden und Zusammenhängen manuell oder durch die Verwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 1600 Seiten.
 

Kurzinfos zu Inhalten einiger Unterprogramme erhalten Sie unter:
 

• Kurzinfos zum Themengebiet Analysis
• Kurzinfos zum Themengebiet Geometrie
• Kurzinfos zum Themengebiet Algebra
• Kurzinfos zum Themengebiet 3D-Mathematik
• Kurzinfos zum Themengebiet Stochastik
• Kurzinfos zum Themengebiet Vektoralgebra
• Kurzinfos zum Themengebiet Trigonometrie
• Kurzinfos zu sonstigen Themengebieten

---

 

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich 3D-Mathematik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Analysis eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in MathProf 5.0 unter dem Themenbereich Vektoralgebra eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in MathProf implementierten Modulen finden Sie, indem Sie den Reiter MathProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
 

 
 

 

 

II - PhysProf 1.1
Physik interaktiv
 

PhysProf 1.1 ist ein Programm für alle, die die Aufgabe oder das Ziel haben, sich physikalische Gesetzmäßigkeiten und Gegebenheiten zu verdeutlichen. Es spricht alle an, die sich für die Ergründung physikalischer Prozessabläufe und derartige Zusammenhänge interessieren. In zahlreichen Unterprogrammen besteht die Möglichkeit, Veränderungen von Einflussgrößen manuell, oder durch die Ausgabe automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren. Inhaltlich umfasst es ca. 70 verschiedene Unterprogramme zu den Fachthemenbereichen Mechanik, Elektrotechnik, Thermodynamik und Optik.
 

 

Durch die Benutzung dieses Programms wird es ermöglicht, bereits bekannte Fachthemeninhalte aufzuarbeiten und entsprechende Sachverhalte numerisch wie auch grafisch zu analysieren. Mittels der freien Veränderbarkeit der Parameter von Einflussgrößen bei der Ausgabe grafischer Darstellungen besteht in vielen Unterprogrammen die Möglichkeit, Veränderungen an dargestellten Zusammenhängen manuell oder durch die Anwendung automatisch ablaufender Simulationsprozesse in Echtzeit zu steuern und zu analysieren.

Es verfügt über eine umfangreiche Programmhilfe mit ca. 300 Seiten.
 

Eine Übersicht aller in PhysProf 1.1 zur Verfügung stehender Programmteile finden Sie im PhysProf - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

 

Kurzinfos zu Inhalten einiger Unterprogramme von Physprof 1.1 erhalten Sie unter:
 

• Kurzinfos zum Themengebiet Mechanik
• Kurzinfos zum Themengebiet Elektrotechnik
• Kurzinfos zum Themengebiet Optik
• Kurzinfos zum Themengebiet Thermodynamik
• Kurzinfos zu sonstigen Themengebieten

---

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Mechanik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Thermodynamik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einem in PhysProf 1.1 unter dem Themenbereich Elektrotechnik eingebundenen Unterprogramm, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Weitere Videos zu einigen in PhysProf implementierten Modulen finden Sie, indem Sie den Reiter PhysProf-Videos wählen, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.
 

 
 

 

 
III - SimPlot 1.0
Visualisierung und Simulation interaktiv
 

SimPlot 1.0 ist eine Anwendung, welche es unter anderem durch interaktiv erstellbare Präsentationen ermöglicht, sich Sachverhalte aus vielen technischen, wissenschaftlichen und anderen Bereichen grafisch darstellen und diese multifunktional sowohl statisch, wie auch in Form bewegter Grafiken ausgeben zu lassen. Das Programm erlaubt die Erstellung von Gebilden mit zweidimensionalen grafischen Objekten, welche als geometrische Figuren und Bilder zur Verfügung stehen.

Es bietet zudem die Möglichkeit, Zusammenhänge im Bereich der Planimetrie auf einfache Weise interaktiv zu analysieren. Unter anderem wird es ermöglicht, mit erzeugten Gebilden geometrische Transformationen durchzuführen und diesen automatisch ablaufende Bewegungs- und Verformungsprozesse zuzuweisen.

 

 
SimPlot kann sowohl zur Erstellung von Infografiken, zur dynamischen Datenvisualisierung, zur Auswertung technisch-wissenschaftlicher Zusammenhänge sowie zur Erzeugung bewegter Bilder für verschiedenste Anwendungsbereiche eingesetzt werden. Neben der Bereitstellung vieler mathematischer Hilfsmittel und zusätzlicher Unterprogramme erlaubt es auch die Einblendung von Hilfslinien zur Echtzeit, welche dienlich sind, um sich relevante Sachverhalte und Zusammenhänge unmittelbar begreiflich zu machen.

Dieses Programm verfügt über eine umfangreiche Programmhilfe mit ca. 900 Seiten.
 

Eine Inhaltsübersicht dessen finden Sie unter SimPlot - Inhaltsverzeichnis, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

 

Beispiele einiger mit Simplot 1.0 erzeugter Grafiken finden Sie unter Beispiele, oder durch einen Klick auf die nachfolgend dargestellte Schaltfläche.

---

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.