MathProf - Krümmung - Höhere Ableitungen - Lokale Extrema

 

Modul Kurvendiskussion - Interaktiv

---

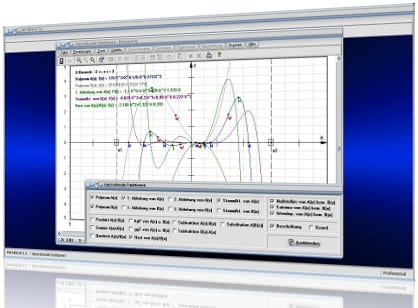
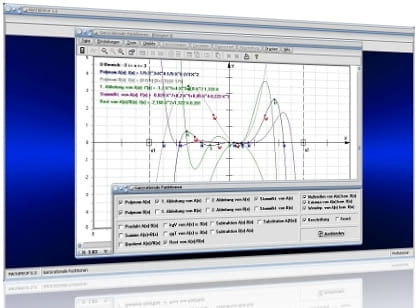
Im Programmteil [Analysis] - [Kurvendiskussion] - Kurvendiskussion - Interaktiv wird die interaktive Durchführung von Analysen zur Bestimmung von Nullstellen, Extrema (Extrempunkten) und Wendepunkten sowie weiterer Eigenschaften mathematischer Funktionen in expliziter Form ermöglicht (Funktionsuntersuchung und Differentialrechnung).

 

Das Programm führt eine numerische Analyse (Differentialrechnung) durch und untersucht hierbei derartige Funktionen auf folgende Punkte und Eigenschaften:

• Nullstellen
• Pole (Polstellen)
• Extremstellen / Extrempunkte (Hochpunkte und Tiefpunkte)
• Wendepunkte (Wendestellen)

 
Grafisch darstellen lassen sich:

• Die zu untersuchende Funktion f(x,p)
• 1. Ableitung f'(x,p) (Steigungsfunktion, Ableitungsfunktion) der zu untersuchenden Funktion f(x,p)
• 2. Ableitung f''(x,p) der zu untersuchenden Funktion f(x,p)
• 3. Ableitung f'''(x,p) der zu untersuchenden Funktion f(x,p)
• Polstellen (Pole) der zu untersuchenden Funktion f(x,p)
• Tangenten in Nullstellen, Extremstellen (Hochpunkten und Tiefpunkten) und Wendepunkten (Wendestellen) der zu untersuchenden Funktion f(x,p)
• Normalen in Nullstellen, Extremstellen (Hochpunkten und Tiefpunkten) und Wendepunkten (Wendestellen) der zu untersuchenden Funktion f(x,p)
• Krümmungskreise durch Nullstellen und Extremstellen  (Extrempunkten) der zu untersuchenden Funktion f(x,p)

 
Nullstellen sind Punkte, in welchen eine Funktion die horizontale Achse des Koordinatensystems schneidet bzw. berührt. Extrempunkte (Hochpunkte und Tiefpunkte) sind Punkte einer Kurve, bei welchen eine Funktion lokale Maxima bzw. Minima besitzt. In Wendepunkten (Wendestellen) liegt eine Änderung der Art der Kurvenkrümmung vor, d.h. eine Kurve geht von einer Links- in eine Rechtskurve, oder umgekehrt, über. Pole sind Definitionslücken besonderer Art. Nähert man sich einer Stelle dieser Art, so strebt der Funktionswert an dieser Stelle gegen plus unendlich oder gegen minus unendlich.

Der in diesem Modul implementierte Ableitungsrechner ermöglicht die Berechnung und Darstellung der Ableitungen erster und höherer Ordnung einer Funktion.
 
Krümmung (Kurvenkrümmung): Die Krümmung einer Kurve in einem Punkt P beschreibt die Stärke mit der die Kurve in unmittelbarer Umgebung des Punktes P vom Verlauf einer Geraden abweicht. Als Krümmungskreis zu einem Punkt P einer ebenen Kurve wird der Kreis bezeichnet, der die Kurve in diesem Punkt am besten annähert. Den Mittelpunkt des Krümmungskreises wird als Krümmungsmittelpunkt bezeichnet. Sein Radius ist der Krümmungsradius (Krümmungshalbmesser).

 

 

Abbildung 1

 

Abbildung 2

Führen Sie eine interaktive Kurvendiskussion folgendermaßen durch:
 

1. Definieren Sie die Funktion, gemäß den geltenden Syntaxregeln, im Eingabefeld mit der Bezeichnung f(x,p) =.
    
2. Bedienen Sie die Schaltfläche Darstellen.
    
3. Bestimmen Sie den zu analysierenden Bereich, indem Sie in die entsprechenden, rechteckig umrahmten Mausfangbereiche klicken und bewegen Sie den Mauscursor bei gedrückt gehaltener Maustaste nach links oder nach rechts (je schmaler der Bereich gewählt wird, desto exakter sind die resultierenden Berechnungsergebnisse).
    
4. Wählen Sie auf dem Bedienformular durch eine Aktivierung des entsprechenden Kontrollkästchens Nullstellen, Extrema, Wendepunkte, Pole aus, ob ermittelte Nullstellen, Extrema, Wendepunkte bzw. Pole der Funktion angezeigt werden sollen.
    
5. Legen Sie durch die Aktivierung/Deaktivierung der Kontrollkästchen 1. Ableitung, 2. Ableitung, 3. Ableitung fest, ob die Darstellung der 1. Ableitung, 2. Ableitung oder 3. Ableitung der Funktion ausgegeben werden soll.
    
6. Möchten Sie sich ggf. die Tangenten oder Normalen, die durch Hoch-, Tief- und Wendepunkte der Funktion verlaufen, zeigen lassen, so aktivieren Sie hierfür das entsprechende Kontrollkästchen Tangenten bzw. Normalen. Um sich Krümmungskreise darstellen zu lassen, die durch Nullstellen oder Extrema verlaufen, aktivieren Sie das Kontrollkästchen Krümmungskreise.
    
7. Sollen die Bereichsgrenzen zur Untersuchung der Funktion mit der Maus verändert werden, so klicken Sie mit der linken Maustaste in den rechteckig umrahmten Mausfangbereich und bewegen den Mauscursor bei gedrückt gehaltener Maustaste nach links oder nach rechts.
    
8. Enthält der Funktionsterm das Einzelzeichen P, so legen Sie, wie unter Verwendung von Funktionsparametern beschrieben, nach einer Bedienung des Schalters Parameter P den zu durchlaufenden Wertebereich für diesen Funktionsparameter, sowie die zu verwendende Schrittweite, fest. Positionieren Sie hierauf den Schieberegler Parameter P, um den Einfluss des Parameters P zu untersuchen.
    
9. Möchten Sie Analysen mit Hilfe von Simulationen durchführen, so wählen Sie durch Aktivierung des entsprechenden Kontrollschalters Bereich oder Parameter P die Art der Simulation die Sie durchführen lassen möchten.
   
   Um den Bereich simulativ verändern, oder eine automatisch ablaufende Parameterwertsimulation durchführen zu lassen, klicken Sie auf die Schaltfläche Simulation. Vor Ausführung der Simulation zur Änderung des Untersuchungsbereichs wird Ihnen ein Formular zur Verfügung gestellt. Beendet werden kann die Ausführung dieser wieder durch eine erneute Betätigung derselben Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.

 

 
Nicht in jedem Fall ist eine eindeutige Bestimmung aller evtl. vorhandener Punkte innerhalb des gewählten Untersuchungsbereichs einer Kurve möglich. Somit kann es vorkommen, dass insbesondere Nullstellen und Wendepunkte nicht ermittelt werden können. Dies kann u.a. bei der Analyse von Kurven auftreten, bei welchen sich viele eng beieinander liegende Stellen dieser Art befinden. Auch kann dies bei derartigen Analysen auftreten, bei welchen an einer Nullstelle kein Vorzeichenwechsel stattfindet.

Um Krümmungskreise nicht oval (ellipsenförmig) dargestellt zu bekommen, wählen Sie bei Ausgabe der grafischen Darstellung den Menüpunkt Einstellungen - Auflösung - Skalierungsart - Linear.

Es werden folgende Bezeichnungskürzel verwendet:

N	Nullstelle
HP	Hochpunkt (Maximum)
TP	Tiefpunkt (Minimum)
W	Wendepunkt (Wendestelle)
KM	Mittelpunkt des Krümmungskreises

 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

Wurde zur Durchführung einer Kurvendiskussion eine Funktion definiert, die kein Einzelzeichen P zur Definition eines Funktionsparameters enthält, so wird bei Ausgabe einer grafischen Darstellung nachfolgend gezeigtes Bedienformular zur Verfügung gestellt.
 

Wurde zur Durchführung einer Kurvendiskussion (beim Differenzieren) eine Funktion definiert, die das Einzelzeichen P zur Definition eines Funktionsparameters enthält, so wird bei Ausgabe einer grafischen Darstellung das nachfolgend gezeigte Bedienformular eingeblendet.

 

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:

• Punkte beschriften: Beschriftung ermittelter Nullstellen, Extrema, Wendepunkte und Kreismittelpunkte ein-/ausschalten
• Koordinaten: Anzeige der Koordinatenwerte ermittelter Nullstellen, Extrema, Wendepunkte und Kreismittelpunkte ein-/ausschalten
• Bereichsmark.: Markierung des Untersuchungsbereichs ein-/ausschalten

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Kurvendiskussion

Mathematische Funktionen II

Tangente – Normale

Tangente – Sekante

 

 
Es gilt, die Funktion f(x) = cos(x/10)²+3·sin(x/3) innerhalb eines Bereichs -10 ≤ x ≤ 10 zu differenzieren und auf Nullstellen, Extremstellen (Maxima und Minima) und Wendepunkte untersuchen zu lassen.

Vorgehensweise und Lösung:

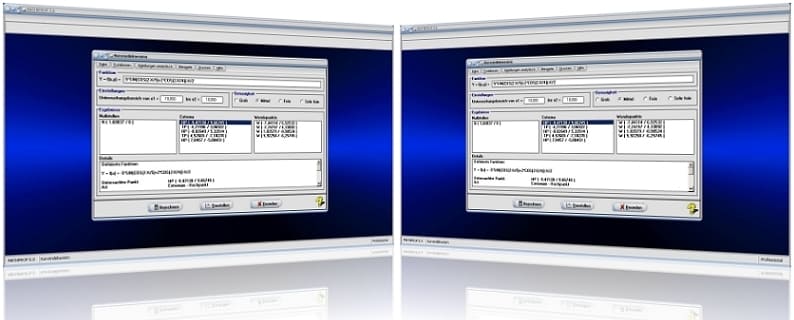
Definieren Sie den Funktionsterm COS(X/10)^2+3*SIN(X/3) im Eingabefeld und bedienen Sie die Schaltfläche Darstellen. Nach einer Aktivierung der Kontrollkästchen Nullstellen, Extrema und Wendepunkte auf dem Bedienformular ermittelt das Programm:

Die Funktion besitzt innerhalb des gewählten Untersuchungsbereichs:

Nullstellen: N1 (-9,041 / 0) ; N2 (-1,009 / 0) ; N3 (9,741 / 0)
Extrema (Extrempunkte): T (-4,964 / -2,216) ; H (4,478 / 3,803)
Wendepunkte: W1 (-9,482 / 0,398) ; W2 (-0,18 / 0,82) ; W3 (9,371 / 0,404)

Nach einer Aktivierung des Kontrollkästchens Krümmungskreise (sowie einer Aktivierung des Menüeintrags Einstellungen - Auflösung - Skalierungsart - Linear) und der Durchführung einer Darstellungsbereichsvergößerung kann entnommen werden, dass die Kurve Krümmungskreise mit folgenden Eigenschaften besitzt:

Krümmungskreis durch Nullstelle N1: Mittelpunkt KM1 (25,09 / 38,15), Radius r = 51,19

Krümmungskreis durch Nullstelle N2: Mittelpunkt KM2 (-21,586 / 21,345), Radius r = 29,649

Krümmungskreis durch Nullstelle N3: Mittelpunkt KM3 (65,643 / 51,408), Radius r = 75,946

 

Krümmungskreis durch Tiefpunkt TP: Mittelpunkt KM4 (-4,964 / 0,897), Radius r = 3,113

Krümmungskreis durch Hochpunkt HP: Mittelpunkt KM5 (4,478 / 0,903), Radius r = 2,9

 

Um weitere Eigenschaftsdetails (z.B. Tangenten, Normalen) der Kurve in den ermittelten Punkten zu erfahren, markieren Sie den sich im Eingabefeld befindenden Funktionsterm, kopieren ihn in die Zwischenablage (mit Tastenkombination Strg-C), öffnen das Unterprogramm Kurvendiskussion positionieren den Mauscursor in das Eingabefeld, verwenden die Tastenkombination Strg-V um den Funktionsterm in das Eingabefeld zu übernehmen und bedienen die dort vorhandene Schaltfläche Berechnen.

 

Klicken Sie den entsprechenden Eintrag in einer obig positionierten Tabelle an, so werden weitere Informationen zu den Eigenschaften dieser Kurve in den entsprechenden Punkten in der unten angeordneten Tabelle ausgegeben.
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3


Grafische Darstellung - Beispiel 4


Grafische Darstellung - Beispiel 5


Grafische Darstellung - Beispiel 6


Grafische Darstellung - Beispiel 7
   

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
 

 
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.

Wikipedia - Kurvendiskussion
Wikipedia - Differentialrechnung
Wikipedia - Tangente
Wikipedia - Ableitung
Wikipedia - Nullstelle
Wikipedia - Extremwert
Wikipedia - Krümmung

  

 

 

Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Segmentweise definierte Funktionen - Kurvenscharen - Funktionsparameteranalyse - Funktionswertetabellen - Iteration - Parameter der Sinus- und Cosinusfunktion - Parameter der Logarithmusfunktion - Parameter der Betragsfunktion - Parameter der Integer-Funktion - Parameter der Quadratwurzelfunktion - Parameter der Potenzfunktion - Parameter der Exponentialfunktion - Kubische Funktion in allgemeiner Form - Kubische Funktion in spezieller Form - Zahlenfolgen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Rekursive Zahlenfolgen - Interaktiv - Arithmetische und geometrische Zahlenfolgen - Parabelgleichungen - Parabelgleichungen - Interaktiv - Parabel und Gerade - Interaktiv - Analyse quadratischer Funktionen - Ermittlung ganzrationaler Funktionen - Ganzrationale Funktionen (Polynome) - Ganzrationale Funktionen (Polynome) - Interaktiv - Gebrochenrationale Funktionen - Gebrochenrationale Funktionen - Interaktiv - Interpolation nach Newton und Lagrange - Interpolation ganzrationaler Funktionen - Polynomregression - Nullstellen - Iterationsverfahren - Horner-Schema - Tangente - Normale - Tangente - Sekante - Tangente und Normale von externem Punkt - Kurvendiskussion - Obersummen und Untersummen - Obersummen und Untersummen - Interaktiv - Integrationsmethoden - Rotationsparaboloid (3D) - Integralrechnung - Integralrechnung - Interaktiv - Zykloide - Hypozykloide - Epizykloide - Sternkurven - Zissoide - Strophoide - Kartesisches Blatt - Semikubische Parabel - Archimedische Spirale - Logarithmische Spirale - Fourier-Summen - Fourier-Reihen - Taylorreihen und Potenzreihen - Implizite Funktionen
 

 

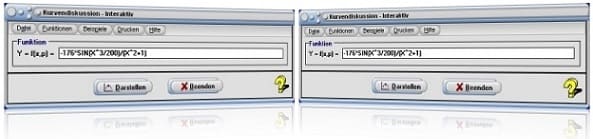
Startfenster des Unterprogramms Kurvendiskussion - Interaktiv
 

MathProf 5.0 - Unterprogramm Kurvendiskussion

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---