MathProf - Kegelstumpf - Hohlzylinder - Kugelsektor - Torus - Zylinder

Fachthemen: Kugel - Kugelsegment - Kugelausschnitt - Kugelkappe - Halbkugel - Kugelsektor - Kugelabschnitt - Kugelschicht - Zylinder - Kreiszylinder - Hohlzylinder - Rohr - Kegel - Kreiskegel - Kegelstumpf - Torus - Doppelkegel - Zylinderabschnitt
MathProf - 3D-Geometrie - Software als Ergänzung zum Unterrichtsmaterial der Mathematik, zum Lösen verschiedenster Aufgaben und zur Visualisierung relevanter Sachverhalte aus der Naturwissenschaft mittels Simulationen, 3D-Animationen für die Schule, das Abitur, das Studium sowie für Lehrer, Ingenieure, Wissenschaftler und alle die sich für Mathematik interessieren.

Online-Hilfe
für das Modul zur Berechnung und interaktiven Analyse von krummflächig begrenzten, mathematisch definierten Raumkörpern (Grundkörpern).
In diesem Teilprogramm kann unter anderem die Flächenberechnung sowie die Volumenberechung geometrischer Körper und Formen dieser Art durchgeführt werden.
Berechnen lassen sich die folgenden Volumenkörper:
Kugel, Kugelsegment (Kugelausschnitt - Kugelkappe - Halbkugel - Kugelkalotte), Kugelsektor (Kugelabschnitt), Kugelschicht, Zylinder (Kreiszylinder bzw. Drehzylinder), Hohlzylinder (Rohr), Kegel (Kreiskegel), Kegelstumpf (Kreiskegelstumpf), Torus, schräg geschnittene Zylinder, Doppelkegel, Zylinderabschnitt (Zylinderhuf) und schiefer Kegel.
Für die entsprechenden Raumgebilde ermittelt das Programm bei Durchführung der Körperberechnung neben vielem anderem deren Oberfläche (Oberflächeninhalt), Querschnittsfläche, Mantelfläche (Mantelflächeninhalt) und Volumen bzw. den Rauminhalt sowie die Werte vieler weiterer Merkmale hinsichtlich derer Raumgeometrie.
Zudem erfolgt die Schwerpunktberechnung der definierten geometrischen Figuren. Der implementierte Rechner gibt nach einer Festlegung der Werte erforderlicher Größen die ermittelten Lösungen des gestellten Problems aus und analysiert weitere Eigenschaften des entsprechenden Gebildes.
Ein frei bewegbares und drehbares, dreidimensionales Koordinatensystem erlaubt die Praktizierung interaktiver Analysen bzgl. Sachverhalten und relevanter Zusammenhänge zu diesem Fachthema. Neben der Durchführung vom Axialschnitt eines dargestellten Gebildes kann bei der Ausgabe der grafischen Darstellung auch die Ausführung verschiedener 3D-Simulationen der geometrischen 3D-Körper veranlasst werden.
Beispiele, welche Aufschluss über die Verwendbarkeit und Funktionalität
dieses Programmmoduls geben und dazu dienlich sind, Aufgaben zu diesem Themengebiet zu lösen, sind implementiert.

Weitere relevante Seiten zu diesem Programm
Durch die Ausführung eines Klicks auf die nachfolgend gezeigte Schaltfläche gelangen Sie zur Startseite dieser Homepage.

Themen und Stichworte I zu diesem Modul:Kegel - Kugelsegment - Kugelausschnitt - Kugelkappe - Halbkugel - Kugelsektor - Kugelabschnitt - Kugelschicht - Zylinder - Kreiszylinder - Hohlzylinder - Rohr - Kreiskegel - Kegelstumpf - Torus - Doppelkegel - Zylinderabschnitt - Zylinderhuf - Schiefer Kegel - Schiefer Kreiskegel - Abgeschnittener Kegel - Kugeloberfläche - Geometrische Körper - Geometrische Grundkörper - Übersicht - Körperberechnung - Dreidimensional - 3D - Volumenberechnung - Volumenberechnungen - Volumen - Rauminhalt - Ansicht - Draufsicht - Seitensicht - Eigenschaften - Oberflächeninhalt - Mantelflächeninhalt - Flächeninhalt - Zylinderfläche - Querschnittsfläche - Massenmittelpunkt - Kegelberechnung - Gerader Kreiskegel - Gerader Kegel - Walze - Mantelfläche - Merkmale - Arten - Halbkugel - Oberfläche - Schwerpunkt - Mantellinie - Konus - Kugelkalotte - Kugelhaube - Kegelverhältnis - Kegelverjüngung - Verjüngung - Verhältnis - Inhalt - Kegelwinkel - Öffnungswinkel - Kegelmantel - Höhe - Volumenformel - Spitze - Kreiskegelstumpf - Dreidimensionale Körper - Durchmesser - Drehen - Rechenformel - Rechenformeln - Begriff - Begriffe - Erklärung - Einfach erklärt - Welche - Welcher - Welches - Wodurch - Herleitung - Beweis - Beschreibung - Mathe - Mathematik - Definition - Gegeben - Gesucht - Seitenfläche - Seitenkante - Vollzylinder - Grundfläche - Kalotte - Drehzylinder |
Themen und Stichworte II zu diesem Modul:Drehkegel - Kreisscheibe - Fläche - Radius - Umfang - Kegelfläche - Oberflächenberechnung - Volumenrechner - Volumenschwerpunkt - Geometrischer Schwerpunkt - Grundflächeninhalt - r1 - r2 - a - b - c - d - a1 - a2 - b1 - b2 - c1 - c2 - d1 - d2 - e - f - h - h1 - h2 - u - r - v - alpha - beta - Axialschnitt - Bild - Grafik - Zylindermantel - Fehlende Größen - Grundkreisradius - Oberflächenformel - Flächeninhaltsformel - Gesamtfläche - Mittelpunkt - Mantel - Schnittfläche - Querschnitt - Abgeschrägter Zylinder - Grundkreis - Deckfläche - Abgeschnitten - Geometrisch - Körper - Bezeichnung - Graph - Formeln - Berechnungsformel - Berechnungsformeln - Berechnen - Grafik - Präsentation - Aufgeschnitten - Aufschneiden - Grundlagen - Verändern - Ändern - Zeichnen - Rechenformel - Volumenformeln - Beschreibung - Bedeutung - Was bedeutet - Untersuchen - Untersuchung - Plotten - Bestimmen - Bilder - Tabelle - Beispiel - Beispielaufgaben - Arbeitsblatt - Arbeitsblätter - Unterrichtsmaterial - Unterrichtsmaterialien - Lernen - Erlernen - Übungsaufgaben - Üben - Übungen - Lösungen - Aufgaben - Lösung - Abituraufgaben - Abiturvorbereitung - Abitur - Abi - Leistungskurs - LK - Klassenarbeit - Klassenarbeiten - Anwendungsaufgaben - Einführung - Satz des Cavalieri - Simulator - Plotter - Formelsammlung - Formelübersicht - Gewicht - Formel - Dichte - Masse - Rechner - Eigenschaften - Darstellung - Berechnung - Darstellen |
Krummflächig begrenzte Raumkörper
Zylinder - Kegel - Hohlzylinder - Torus - Kegelstumpf - Kugelsegment - Kugelsektor

Modul Krummflächig begrenzte Körper
Das Unterprogramm [Geometrie] - Krummflächig begrenzte Körper ermöglicht die Berechnung, sowie die dreidimensionale Darstellung verschiedener mathematischer krummflächig begrenzter Körper (Raumgebilde). Hierzu zählen u.a. die Flächenberechnung und die Volumenberechnung der entsprechenden Gebilde.

Ein Körper ist die Menge aller Punkte, Geraden und Ebenen im dreidimensionalen Raum, die sich innerhalb eines vollständig abgeschlossenen Teils des Raumes befinden. Die Oberfläche eines Körpers ist die Summe aller seiner Begrenzungsflächen. Als Rauminhalt oder Volumen eines Körpers wird die Größe des Raums bezeichnet, welche von seinen Begrenzungsflächen eingeschlossen wird. Krummflächig begrenzte Körper werden ganz, oder teilweise von krummen Flächen begrenzt.
Untersuchungen und Berechnungen können in diesem Unterprogramm mit nachfolgend aufgeführten Körpern durchgeführt werden:
- Kugel
- Kugelsegment (Kugelabschnitt - Kugelkappe - Halbkugel)
- Kugelsektor (Kugelausschnitt)
- Kugelschicht
- Zylinder (Kreiszylinder)
- Hohlzylinder (Rohr)
- Kegel (Kreiskegel)
- Kegelstumpf
- Torus
- Zylinder - schräg geschnitten
- Doppelkegel Variante 1
- Doppelkegel Variante 2
- Zylinderabschnitt (Zylinderhuf)
- Schiefer Kegel (Schiefer Kreiskegel)
Beschreibung - Definition - Zylinder - Hohlzylinder - Kegel - Kreiskegelstumpf - Kugel - Kugelsegment - Kugelschicht - Kugelsektor
Als geometrische Körper werden die Mengen aller Punkte, Geraden und Ebenen des dreidimensionalen Raums bezeichnet, die sich innerhalb eines vollständig abgeschlossenen Teils dessen befinden.
Als geometrische Grundkörper sind die dreidimensionalen Körper Würfel, Quader, Prisma, Pyramide, Zylinder, Kegel und Kugel definiert.
Zylinder: Ein gerader Zylinder (gerader Kreiszylinder oder Walze) ist ein krümmflächig begrenzter geometrischer Körper, welcher von zwei parallelen zueinander kongruenten Kreisflächen sowie einer krummen Fläche (Mantelfläche) begrenzt wird, bei deren Abwicklung in der Ebene hieraus ein Rechteck entsteht. Stehen die Mantellinien eines Zylinders senkrecht auf dessen Grundfläche, so wird dieser Zylinder als gerader Zylinder (gerader Rotationszylinder), oder Kreiszylinder, Vollzylinder bzw. Drehzylinder bezeichnet. Trifft dies nicht zu, so heißt der Zylinder schiefer Zylinder.
Die Anordnung dieser unendlich vielen gleich langen Mantellinien wird als Mantel bezeichnet. Alle zur vertikalen Achse des Zylinders senkrechten Ebenen schneiden diesen in Kreisen, welche als Parallelkreise bezeichnet werden. Die Entfernung der beiden begrenzenden Kreiszylinder wird Höhe genannt.
Hohlzylinder: Wird aus einem Zylinder ein kleinerer Zylinder auf diese Weise herausgebohrt, dass die Grundflächen dieser beiden Zylinder konzentrische Kreisflächen bilden, so verbleibt ein Restkörper, welcher als Hohlzylinder oder Rohr bezeichnet wird.
Schräg abgeschnittener Zylinder: Wird ein Kreiszylinder von einer Ebene geschnitten, welche nicht parallel zur Ebene der Grundfläche dessen liegt, so entsteht ein schief abgeschnittener Kreiszylinder, dessen Schnittfläche eine Ellipse ist. Der hierbei entstehende Körper wird als schief abgeschnittener Kreiszylinder bezeichnet.
Kegel: Wird ein rechtwinkliges Dreieck solange um eine seiner Katheten gedreht, bis sich dieses wieder in seiner Ursprungslage befindet, so entsteht ein Rotationskörper, welcher als Kegel, Drehkegel oder Kreiskegel bezeichnet wird. Die Oberfläche dessen bildet sich aus dem von ihm beschriebenen Grundkreis sowie aus dem von der Hypotenuse des rotierenden Dreiecks beschriebenen Mantels.
Der Abstand der Spitze des Kegels von dessen Grundfläche (dem Grundkreis) ist die Höhe des Kegels. Befindet sich die Spitze des Kegels senkrecht über dem Mittelpunkt des Grundkreises dessen, so wird der Kegel als gerader Kegel oder gerader Kreiskegel bezeichnet. Trifft dies nicht zu, so heißt der Kegel schiefer Kegel oder schiefer Kreiskegel.
Kegelstumpf: Ein Kreiskegelstumpf (Kegelstumpf) entsteht, wenn ein Kreiskegel von einer zu seiner Grundfläche parallelen Ebene in einem Abstand h < hKegel geschnitten wird und die Spitze dessen entfernt wird. Ein Kegelstumpf wird auch als abgeschnittener Kegel bezeichnet.
Kugel: Wird ein Kreis oder Halbkreis um seinen Durchmesser gedreht, so beschreibt die Peripherie des Kreises eine Kugelfläche. Der von der Kugelfläche vollständig abgeschlossene Teil des Raums wird als Kugel bezeichnet. Die Kugelfläche (Kugeloberfläche) ist der geometrische Ort aller Punkte des Raums, die von einem Punkt M aus einen konstanten Abstand besitzen.
Kugelsegment: Kugelsegmente entstehen, wenn eine Kugel von einer beliebigen Ebene geschnitten wird. Sie sind gleich groß, wenn die schneidende Ebene durch den Mittelpunkt der Kugel verläuft. Ein Kugelsegment wird auch als Kugelabschnitt oder Kugelkappe bezeichnet. Eine Halbkugel ist ein geometrischer Körper, der entsteht, wenn eine Kugel mit einem geraden Schnitt durch ihren Mittelpunkt in zwei Teile zerlegt wird.
Kugelschicht: Wird eine Kugel von zwei zueinander parallel liegenden Ebenen geschnitten, so schneiden diese eine Kugelschicht aus dieser. Das hierbei aus der Kugeloberfläche geschnittene Gebilde heißt Kugelzone.
Kugelsektor (Kugelausschnitt): Wenn der Radius einer Kugel entlang eines auf der Kugel liegenden Kleinkreises in Form einer Leitkurve gleitet, so beschreibt er eine Kegelfläche. Er teilt die Kugel in zwei Ausschnitte, welche als Kugelsektoren (Kugelausschnitte) bezeichnet werden. Stellt diese Leitkurve einen Großkreis dar, so entstehen zwei Halbkugeln.
Torus: Bei einem Torus handelt es sich um einen geometrischen Körper, der sich bildet, wenn ein vertikal ausgerichteter Kreis um eine vertikal ausgerichtete Achse rotiert, die sich außerhalb des Kreises befindet.
Doppelkegel: Ein Doppelkegel mit einander entgegengesetzten Spitzen entsteht in Form der Rotationsfläche einer Geraden, die sich um eine sie nicht rechtwinkelig schneidende Achse bildet.
Zylinderabschnitt (Zylinderhuf): Als Zylinderabschnitt (Zylinderhuf) wird ist ein mit einer Ebene schräg abgeschnittener Kreiszylinder bezeichnet.
Formeln - Formelsammlung - Formelübersicht
Nachfolgend aufgeführt sind Formeln, die zur Berechnung der Werte entsprechender Größen eines Körpers benötigt werden.
Durchmesser: d = 2·r
Oberfläche: A = 4·π·r²
Volumen: V = 4/3·π·r³
Mit:
r: Radius der Kugel
Kugelsektor:
Radius Kugelsektor: rk = √ h·( 2·r-h )
Fläche Kugelsektor: A = π·r·(2·h+b )
Volumen Kugelsektor: V = 2·π·r²· h/3
Mit:
h: Höhe des Kugelsegments
r: Radius des Kugelsegments
b: Radius des Kugelsegments
Kugelsegment:
Radius Kugelsegment: rk = √ h · ( 2·r - h )
Fläche Kugelsegment: A = π·( 2·r·h + b² )
Grundfläche: AG = 2·π·r·h
Volumen: V = π/ 3·h²·( 3·r-h )
Mit:
h: Höhe des Kugelsegments
r: Radius der Kugel
b: Radius des Kugelsegments
Kugelschicht:
Kugelradius: r = √ a1² + [ ( a1² - a2² - h² ) / 2h ]²
Vert. Abstand der Schicht zu Kugelmittelpunkt: h1 = ( a1² - a2² - h² ) / 2h
Vert. Abstand der Schicht zu oberstem Kugelpunkt: h2 = r - h - m
Mantelfläche: M = 2·π·r·h
Oberfläche: A = π ·( 2·r·h + a1² + a2² )
Volumen: V = π·h / 6·( 3·a1² + 3·a2² + h² )
Mit:
a1: Radius des unteren (größeren) Grenzkreises der Schicht
a2: Radius des oberen (kleineren) Grenzkreises der Schicht
h: Höhe der Kugelschicht
m: Abstand der unteren Schicht zur Kugelmitte
Zylinder:
Durchmesser: d = √ h² + ( 2·r )²
Oberfläche: A = 2·π·r·( h + r )
Mantelfläche (Zylindermantel): M = 2·π·r·h
Volumen: V = π·r²·h
Mit:
r: Radius der Kugel
h: Höhe der Kugelschicht
Hohlzylinder:
Wanddicke: b = R - r
Oberfläche: A = 2·π·( R + r ) · ( R - r + h )
Mantelfläche: M = 2·π·h·( R + r )
Volumen: V = π·h·( R² - r² )
Mit:
R: Außenradius des Hohlzylinders
r: Innenradius des Hohlzylinders
h: Höhe des Hohlzylinders
Kegel:
Mantellinie: m = √ h² + r²
Mantelfläche: M = r·m·π
Oberfläche: A = r·π·( r + m )
Volumen: V = 1/3·r²·π·h
Öffnungswinkel: α = 2·arcsin( r / m )
Mit:
h: Höhe des Kegels
r: Radius der Grundfläche des Kegels
Kegelstumpf:
Mantellinie: m = √ ( R - r )² + h²
Mantelfläche: M = ( R + r )·π·m
Oberfläche: A = M + π·r² + π·R²
Volumen: V = h / 3·π·( R² + R·r + r² )
Mit:
R: Radius der Grundfläche
r: Radius der Deckfläche
h: Höhe
Torus:
Innenradius: rI = R - r
Breite des Torus: b = 2·( R + r )
Oberfläche: A = 4·π²·R·r
Volumen: V = 2·π²·R·r²
Mit:
R: Großer Radius des Torus
r: Kleiner Radius des Torus
Doppelkegel:
Durchmesser: d = 2·r
Gesamthöhe: H = 2·h
Oberfläche: A = 2·r· π·√ h² + r²
Volumen: V = 2/3·r²·π·h
Mit:
h: Halbhöhe des Doppelkegels
r: Radius des Doppelkegels
Fachworte
Im Folgenden sind einige in diesem Zusammenhang häufiger verwendete Fachworte kurz erklärt.
Zylinderfläche: Der Begriff Zylinderfläche bezeichnet die Oberfläche eines Zylinders.
Volumenschwerpunkt (geometrischer Schwerpunkt): Der geometrische Schwerpunkt von Linien wird als Linienschwerpunkt, von Flächen als Flächenschwerpunkt und von Körpern als Volumenschwerpunkt bezeichnet. Der Volumenschwerpunkt entspricht bei homogenen Körpern dem Massenmittelpunkt. Der geometrische Schwerpunkt ist ein Graviationszentrum.
Körperberechnungen: Als Körperberechnung wird in der Mathematik die Berechnung geometrischer Körper bezeichnet.
Volumenberechnungen: Als Volumenberechnung wird in der Mathematik die Berechnung von Volumina geometrischer Körper bezeichnet.
Oberflächeninhalte: Der Oberflächeninhalt eines geometrischen Körpers entspricht der Summe der Flächeninhalte aller einzelnen in diesem enthaltenen Oberflächen.
Querschnittsfläche: Als Querschnittsfläche eines Körpers wird die Fläche bezeichnet, die vertikal zu einer bestimmten Richtung oder Achse verläuft und den Querschnitt des Körpers darstellt.
Mantelfläche: Als Mantelfläche (Mantel) wird ein Teil der Oberfläche bestimmter Körper bezeichnet. Deren Deck- und Bodenfläche werden nicht zur Berechnung der Mantelfläche einbezogen.
Zylindermantel: Mit dem Begriff Zylindermantel wird die Mantelfläche eines Zylinders beschrieben.
Kegelmantel: Mit der Bezeichnung Kegelmantel wird die Mantelfläche eines Kegels beschrieben.
Kegelfläche: Die Begriff Kegelfläche bezeichnet die geamte Oberfläche eines Kegels. Hierzu zählen sowohl die Mantelfläche wie auch die Grundfläche dessen.
Kreisscheibe: Bei einer Kreisscheibe handelt es sich um einen Zylinder, der eine geringe Höhe besitzt.
Axialschnitt: Ein Axialschnitt liegt vor, wenn ein achsensymmetrischer Körper entlang der Ebene, die durch dessen Symmetrieachse verläuft, geschnitten wird.
Grundkreisradius: Der Grundkreisradius ist der Radius des Kreises den ein zylinderförmiger Körper als Deck- oder Bodenfläche besitzt.
Grundkante: Grundkanten sind die Kanten einer Grundfläche.
Seitenfläche: Seitenflächen sind Flächen die einen geometrischen Körper seitlich begrenzen.
Seitenkante: Seitenkanten sind die Kanten, die eine Seitenfläche begrenzen.
Konus: Ein Konus ist als Form eines geometrischen Körpers betrachtet ein steilflankiger Kegel, der über keine Spitze verfügt.
Kugelkalotte (Kalotte): Als Kugelkalotte, Kalotte oder Kugelhaube wird der gekrümmte Teil der Oberfläche eines Kugelsegments bezeichnet.
Gewicht - Dichte - Masse - Formel
Das Gewicht eines Körpers errechnet sich aus der Masse dessen sowie der Dichte des Materials aus welchem er besteht.
Seine Dichte kann wie folgt berechnet werden:
ρ = m/V
Sein Gewicht errechnet sich mit:
G = m · g
ρ: Dichte des Materials des Körpers [kg/dm³]
m: Masse des Körpers [kg]
V: Volumen des Körpers [dm³]
g: Erdbeschleunigung = 9,81 m/s²
Kegelverhältnis - Kegelverjüngung - Kegelwinkel
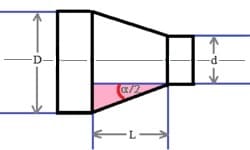
Mit dem Kegelverhältnis C = 1:x wird das Verhältnis des Kegeldurchmessers zur Kegellänge bezeichnet. Es wird aus der Differenz der beiden Durchmesser D und d des Kegels dividiert durch den Abstand dieser beiden Durchmesser berechnet. Eine Kegelverjüngung wird mittels dem Kegelverhältnis C oder durch den Kegelwinkel α angegeben. Es gilt:
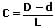
Für den Öffnungswinkel α des Kegels gilt der trigonometrische Zusammenhang:
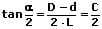
Der Kegelwinkel (Öffnungswinkel des Kegels) α errechnet sich somit folgendermaßen:
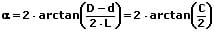
Beträgt der große Durchmesser D des Kegels 50 mm, der kleine Durchmesser dessen 5 mm und seine Länge 200 mm, so errechnet sich sein Öffnungswinkel α wie folgt:
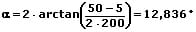
Schwerpunkt eines Körpers - Massenmittelpunkt
Unter dem Schwerpunkt (Massenmittelpunkt) eines Körpers wird der Angriffspunkt der Resultierenden aller seiner einzelnen Teilgewichtskräfte verstanden. Dieser muss nicht innerhalb dessen liegen, sondern kann sich auch außerhalb des Körpers befinden. Für homogene Körper können dessen Koordinaten wie folgt bestimmt werden:
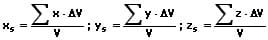
Handelt es sich um einen nichthomogenen Körper dessen Schwerpunkt zu ermitteln ist, so ist eine Zerlegung dessen in seine Teilvolumina erforderlich. Ist dies nicht möglich, so sind differentielle Volumenelemente zu bilden und sein Schwerpunkt ist wie folgt zu berechnen:
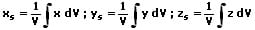
Satz des Cavalieri
Satz des Cavalieri:
Körper die zwischen den Flächen x = a und x = b liegen, haben gleiches Volumen, wenn die Inhalte ihrer Querschnitte für jedes x ∈ <a,b> übereinstimmen.
Screenshots

Grafische Darstellung - Beispiel 1 - Doppelkegel

Grafische Darstellung - Beispiel 2 - Doppelkegel

Grafische Darstellung - Beispiel 3 - Hohlzylinder

Grafische Darstellung - Beispiel 4 - Kegel

Grafische Darstellung - Beispiel 5 - Kegelstumpf

Grafische Darstellung - Beispiel 6 - Kugel

Grafische Darstellung - Beispiel 7 - Kugelschicht

Grafische Darstellung - Beispiel 8 - Kugelkappe

Grafische Darstellung - Beispiel 9 - Kugelsektor

Grafische Darstellung - Beispiel 10 - Schiefer Kegel

Grafische Darstellung - Beispiel 11 - Torus

Grafische Darstellung - Beispiel 12 - Zylinder

Grafische Darstellung - Beispiel 13 - Schräg geschnittener Zylinder

Grafische Darstellung - Beispiel 14 - Zylinderhuf
Körperberechnung und Darstellung

Gehen Sie folgendermaßen vor, um Berechnungen mit den zuvor beschriebenen krummflächig begrenzten Körpern durchzuführen und sich diese darstellen zu lassen:
- Wählen Sie, durch die Fokussierung des entsprechenden Eintrags in der Tabelle, den Körper mit dem Berechnungen durchgeführt werden sollen.
- Geben Sie die erforderlichen Werte der Größen in die dafür vorgesehenen Felder ein. Bedienen Sie ggf. zuvor die Schaltfläche Löschen.
- Führen Sie einen Klick auf die Schaltfläche Berechnen aus.
- Wählen Sie mit Hilfe der aufklappbaren Auswahlbox Auswahl, die Art wie Sie Körper dargestellt bekommen möchten. Hierzu stehen die weiter unten aufgeführten Möglichkeiten zur Verfügung.
- Soll der Schwerpunkt des Körpers angezeigt werden, so aktivieren Sie das Kontrollkästchen Schwerpunkt. Um einen Körper ohne Grund- bzw. Deckfläche(n) darstellen zu lassen, aktivieren Sie das Kontrollkästchen Ohne Grund- und Deckfläche.
- Bedienen Sie hierauf die Schaltfläche Darstellen, um sich den Körper grafisch ausgeben zu lassen.
- Auf dem Bedienformular wird bei Ausgabe der grafischen Darstellung die Möglichkeit geboten, einen dargestellten Körper plan bzgl. der x-z-Ebene (bis zu dessen Mitte) aufzuschneiden und somit sein "Inneres" zu untersuchen. Benutzen Sie hierfür den Rollbalken mit der Bezeichnung Schnitt bei y =.
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.
Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu. Des Weiteren eignet es sich beim Üben dazu, um das Erlernte hinsichtlich praktizierter Übungen bzw. bearbeiteter Übungsaufgaben zu überprüfen und hierzu erworbenes Wissen festigen zu können.
Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).
Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden. Dieses Programm kann auch dabei behilflich sein, einen Begriff zum entsprechenden Fachthema zu erklären.
Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.
Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.
Mathematische Funktionen I - Mathematische Funktionen II - Funktionen in Parameterform - Funktionen in Polarform - Kurvenscharen - Funktionsparameter - Kubische Funktionen - Zahlenfolgen - Interaktiv - Rekursive Zahlenfolgen - Interaktiv - Quadratische Funktionen - Interaktiv - Parabel und Gerade - Interaktiv - Ganzrationale Funktionen - Interaktiv - Gebrochenrationale Funktionen - Interaktiv - Kurvendiskussion - Interaktiv - Ober- und Untersummen - Interaktiv - Integralrechnung - Interaktiv - Hypozykoide - Sinusfunktion und Cosinusfunktion - Fourier-Reihen - Implizite Funktionen - Zweipunkteform einer Gerade - Kreis und Punkt - Interaktiv - Kegelschnitte in achsparalleler Lage - Interaktiv - Rechtwinkliges Dreieck - Interaktiv - Allgemeines Dreieck - Interaktiv - Höhensatz - Eulersche Gerade - Richtungsfelder von Differentialgleichungen - Addition und Subtraktion komplexer Zahlen - Binomialverteilung - Interaktiv - Galton-Brett - Satz des Pythagoras - Bewegungen in der Ebene - Dreieck im Raum - Würfel im Raum - Torus im Raum - Schiefer Kegel - Pyramide - Pyramidenstumpf - Doppelpyramide - Hexaeder - Dodekaeder - Ikosaeder - Abgestumpftes Tetraeder - Abgestumpftes Ikosidodekaeder - Johnson Polyeder - Punkte im Raum - Strecken im Raum - Rotationskörper - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die X-Achse - Rotationskörper - Parametergleichungen - Rotation um die Y-Achse - Flächen im Raum I - Flächen im Raum II - Analyse impliziter Funktionen im Raum - Flächen in Parameterform I - Flächen in Parameterform II - Flächen mit Funktionen in Kugelkoordinaten I - Flächen mit Funktionen in Kugelkoordinaten II - Flächen mit Funktionen in Zylinderkoordinaten - Raumkurven I - Raumkurven II - Raumkurven III - Quadriken - Ellipsoid - Geraden im Raum I - Geraden im Raum II - Ebene durch 3 Punkte - Ebenen im Raum - Kugel und Gerade - Kugel - Ebene - Punkt - Raumgittermodelle
Berechnung
Nachfolgend aufgeführt finden Sie die zur Durchführung einer numerischen Berechnung benötigten Eingabewerte, sowie die vom Programm numerisch ermittelten Berechnungsergebnisse.
Kugel
Erforderliche Eingaben:
- Radius der Kugel r
Ermittelte Ergebnisse:
- Umfang der Kugel U (Kugelumfang)
- Oberfläche der Kugel A (Kugeloberfläche)
- Volumen der Kugel V (Kugelvolumen - Rauminhalt)
- Koordinaten des Schwerpunkts S der Kugel
Kugelsegment und Halbkugel
Erforderliche Eingaben:
- Radius r der Kugel
- Höhe h
Ermittelte Ergebnisse:
- Mantelfläche (Oberfläche) Am des Kugelsegments
- Schnittfläche As des Kugelsegments
- Gesamtoberfläche Ao (Kugelfläche) des Kugelsegments
- Abschnittradius rho des Kugelsegments
- Umfang U der Kugel
- Volumen (Rauminhalt) V des Kugelsegments
- Koordinaten des Schwerpunkts S des Kugelsegments
Kugelsektor
Erforderliche Eingaben:
- Radius r der Kugel
- Höhe h
Ermittelte Ergebnisse:
- Mantelfläche (Mantelflächeninhalt) Am des Kugelsektors
- Schnittfläche As des Kugelsektors
- Gesamtoberfläche (Oberflächeninhalt) Ao des Kugelsektors
- Abschnittradius rho des Kugelsektors
- Umfang U der Kugel
- Volumen (Rauminhalt) V des Kugelsektors
- Koordinaten des Schwerpunkts S des Kugelsektors
Kugelschicht
Erforderliche Eingaben:
- Radius der Kugel r
- Höhe h1
- Höhe h2
Ermittelte Ergebnisse:
- Höhe h der Kugelschicht
- Radius r1 des oberen Schnittkreises der Kugelschicht
- Radius r2 des unteren Schnittkreises der Kugelschicht
- Schnittfläche oben A1 der Kugelschicht
- Schnittfläche unten A2 der Kugelschicht
- Mantelfläche (Mantelflächeninhalt) Am der Kugelschicht
- Gesamtoberfläche (Oberflächeninhalt) Ao der Kugelschicht
- Umfang U der Kugel
- Volumen (Rauminhalt) V der Kugelschicht
- Koordinaten des Schwerpunkts S der Kugelschicht
Zylinder (Kreiszylinder)
Erforderliche Eingaben:
- Radius des Zylinders r
- Höhe h
Ermittelte Ergebnisse:
- Umfang U des Zylinders (Zylinderumfang)
- Grundfläche Ag des Zylinders
- Mantelfläche (Mantelflächeninhalt) Am des Zylinders
- Gesamtoberfläche Ao des Zylinders (Zylinderoberfläche - Oberflächeninhalt)
- Volumen (Rauminhalt) V des Zylinders (Zylindervolumen)
- Koordinaten des Schwerpunkts S des Zylinders
Hohlzylinder
Erforderliche Eingaben:
- Außenradius des Hohlzylinders r1
- Innenradius des Hohlzylinders r2
- Höhe h des Hohlzylinders
Ermittelte Ergebnisse:
- Umfang Ui des Innenzylinders
- Umfang Ua des Außenzylinders
- Mantelfläche (Mantelflächeninhalt) Mi des Innenzylinders
- Mantelfläche (Mantelflächeninhalt) Ma des Außenzylinders
- Boden- bzw. Deckfläche Ab
- Gesamtoberfläche (Oberflächeninhalt) Ao des Hohlzylinders
- Mittlerer Radius rm
- Wanddicke w des Hohlzylinders
- Volumen (Rauminhalt) V des Hohlzylinders
- Koordinaten des Schwerpunkts S des Hohlzylinders
Kreiskegel (Kegel)
Erforderliche Eingaben:
- Radius r des Kreises der Bodenfläche
- Höhe h des Kegels
Ermittelte Ergebnisse:
- Mantelfläche (Mantelflächeninhalt) Am des Kegels
- Grundfläche Ag des Kegels
- Gesamtoberfläche (Oberflächeninhalt) Ao des Kegels
- Länge s der Seitenlinie (Mantellinie)
- Umfang Uk des Grundkreises
- Neigungswinkel der Seitenlinie des Kegels (in Grad)
- Volumen (Rauminhalt) V des Kegels
- Koordinaten des Schwerpunkts S des Kegels
Kegelstumpf
Erforderliche Eingaben:
- Radius r2 des Kreises der Deckfläche
- Radius r1 des Kreises der Bodenfläche
- Höhe h des Kegelstumpfs
Ermittelte Ergebnisse:
- Fläche A1 des Kreises der Bodenfläche des Kegelstumpfs
- Fläche A2 des Kreises der Deckfläche des Kegelstumpfs
- Mantelfläche (Mantelflächeninhalt) Am des Kegelstumpfs
- Gesamtoberfläche (Oberflächeninhalt) Ao des Kegelstumpfs
- Länge s der Seitenlinie des Kegelstumpfs
- Umfang des Kreises der Deckfläche Uo des Kegelstumpfs
- Umfang des Kreises der Bodenfläche Uu des Kegelstumpfs
- Neigungswinkel der Seitenlinie des Kegelstumpfs (in Grad)
- Volumen (Rauminhalt) V des Kegelstumpfs
- Koordinaten des Schwerpunkts S des Kegelstumpfs
Torus
Erforderliche Eingaben:
- Radius r1
- Radius r2
Ermittelte Ergebnisse:
- Oberfläche des Torus Ao
- Umfang Ui des Innenumkreises des Torus
- Umfang Ua des Außenumkreises des Torus
- Volumen (Rauminhalt) V des Torus
- Koordinaten des Schwerpunkts S des Torus
Zylinder schräg geschnitten
Erforderliche Eingaben:
- Radius des Zylinders r
- Höhe h1
- Höhe h2
Ermittelte Ergebnisse:
- Mantelfläche (Mantelflächeninhalt) Am des schräg geschnittenen Zylinders
- Grundfläche Au des Zylinders
- (Schräg geschnittene) Deckfläche Ad des Zylinders
- Gesamtoberfläche (Oberflächeninhalt) Ao des schräg geschnittenen Zylinders
- Umfang U des Zylinders
- Neigungswinkel der Deckfläche des Zylinders (in Grad)
- Volumen (Rauminhalt) V des schräg geschnittenen Zylinders
- Koordinaten des Schwerpunkts S des schräg geschnittenen Zylinders
Doppelkegel I
Erforderliche Eingaben:
- Radius des Kegels r
- Höhe des Doppelkegels h
Ermittelte Ergebnisse:
- Mantelfläche (Mantelflächeninhalt) Am des Doppelkegels
- Länge s der Seitenlinie des Doppelkegels
- Umfang U des Grundkreises des Doppelkegels
- Neigungswinkel der Seitenlinie des Doppelkegels (in Grad)
- Volumen (Rauminhalt) V des Doppelkegels
- Koordinaten des Schwerpunkts S des Doppelkegels
Zylinderabschnitt
Erforderliche Eingaben:
- Radius r des Zylinders
- Höhe h des Zylinderabschnitts
- Länge a des Lots auf die Hufkante des Zylinderabschnitts
Ermittelte Ergebnisse:
- Hufkante b
- Horiz. Mittelpunktwinkel des Grundrisses (in Grad)
- Volumen (Rauminhalt) V des Zylinderabschnitts
- Mantelfläche (Mantelflächeninhalt) M des Zylinderabschnitts
Schiefer Kegel
Erforderliche Eingaben:
- Radius des Kreises der Bodenfläche
- Höhe h des Kegels (Kreiskegels)
- Koordinatenwerte (bzgl. der x-y-Ebene) des Mittelpunkts der Spitze M (x / y) des Kegels (Kreiskegels)
Ermittelte Ergebnisse:
- Mantelfläche (Mantelflächeninhalt) Am des Kegels (Kreiskegels)
- Grundfläche Ak des Kegels (Kreiskegels)
- Gesamtoberfläche (Oberflächeninhalt) Ao des Kegels (Kreiskegels)
- Umfang Uk des Grundkreises des Kegels (Kreiskegels)
- Volumen (Rauminhalt) V des Kegels (Kreiskegels)
- Koordinaten des Schwerpunkts S des Kegels (Kreiskegels)
Doppelkegel II
Erforderliche Eingaben:
- Oberer Radius r1 des Doppelkegels
- Obere Höhe h1 des Doppelkegels
- Unterer Radius r2 des Doppelkegels
- Untere Höhe h2 des Doppelkegels
Ermittelte Ergebnisse:
- Mantelfläche (Mantelflächeninhalt) Am des oberen Kegels (Kreiskegels)
- Länge der Seitenlinie s des oberen Kegels (Kreiskegels)
- Umfang Uk des Grundkreises des oberen Kegels (Kreiskegels)
- Neigungswinkel der Seitenlinie des oberen Kegels (Kreiskegels) (in Grad)
- Volumen (Rauminhalt) V des oberen Kegels (Kreiskegels)
- Mantelfläche (Mantelflächeninhalt) Am des unteren Kegels (Kreiskegels)
- Länge s der Seitenlinie des unteren Kegels (Kreiskegels)
- Umfang Uk des Grundkreises des unteren Kegels (Kreiskegels)
- Neigungswinkel der Seitenlinie des unteren Kegels (Kreiskegels) (in Grad)
- Volumen V des unteren Kegels (Kreiskegels)
Darstellungsbereich
Bei der Darstellung von Gebilden ermöglicht das Programm die Bemessung des Darstellungsbereichs auf eine der folgenden Arten und Weisen:
-
Automatisch
-
Statisch
-
Automatisch:
Wird die Einstellung Automatisch durch die Aktivierung des dafür vorgesehenen Kontrollschalters gewählt, so ermittelt das Programm alle zur vollständigen Darstellung des Körpers erforderlichen x-, y- und z-Koordinatenwerte automatisch und bemisst den Darstellungsbereich dementsprechend.
-
Statisch:
Wird der Kontrollschalter Statisch aktiviert, so verwendet das Programm bei Aufruf der Darstellung den unter Abs. Bereich voreingestellten Darstellungsbereich und beschneidet den Körper an Stellen, die außerhalb dessen liegen. Diesen Bereich können Sie bei Ausgabe der Darstellung verändern, indem Sie den auf dem Bedienformular zur Verfügung stehenden Rollbalken Zoom positionieren. Der maximal einstellbare Wert entspricht dem Doppelten des unter Abs. Bereich auf dem Hauptformular des Unterprogramms vorgegebenen Werts.
Darstellung - Optionen
Durch die Bedienung der aufklappbaren Auswahlbox im Formularbereich Darstellung - Optionen werden zudem folgende Optionen zur Verfügung gestellt, das Layout eines dargestellten Körpers zu beeinflussen:
-
Gefüllt - Kanten als Rohre: Darstellung der Körperkanten als Rohre
-
Gefüllt - Ohne Kantenmarkierung: Darstellung der Körperkanten ohne Begrenzungsmarkierung
Allgemein
Grundlegendes zum Umgang mit dem Programm bei der Ausgabe dreidimensionaler grafischer Darstellungen erfahren Sie unter Dreidimensionale Grafiken - Handling. Wie Sie das Layout einer 3D-Darstellung konfigurieren können, erfahren Sie unter 3D-Layoutkonfiguration.
Weitere Themenbereiche
Eben- und krummflächig begrenzte Körper
Beispiele - Aufgaben
Beispiel 1 - Kugel:
Gegeben sei eine Kugel, von welcher der Wert folgender Größe bekannt ist:
Radius der Kugel: r = 3
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach Auswahl des Tabelleneintrags Kugel, der Eingabe des Werts für den Radius r der Kugel und einer Bedienung der Schaltfläche Berechnen gibt das Programm aus:
Umfang U: 18,85
Oberfläche A (Kugelobefläche): 113,097 FE
Volumen V (Kugelvolumen): 113,097 VE
Koordinaten des Schwerpunkts: S (0 / 0 / 0)
Beispiel 2 - Kugelsegment:
Gegeben sei ein Kugelsegment, von welchem die Werte folgender Größen bekannt sind:
Radius der Kugel: r = 3
Höhe: h = 2,5
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach Auswahl des Tabelleneintrags Kugelsegment, der Eingabe der Werte für den Radius r der Kugel sowie für die Höhe h des Kugelsegments und einer Bedienung der Schaltfläche Berechnen ermittelt das Programm:
Mantelfläche Am: 47,124 FE
Schnittfläche As: 27,489 FE
Gesamtoberfläche Ao: 74,613 FE
Abschnittradius rho: 2,958
Umfang der Kugel U: 18,85
Volumen des Kugelsegments V: 42,542 VE
Koordinaten des Schwerpunkts des Kugelsegments: S (0 / 0 / 1,413)
Beispiel 3 - Kugelsektor:
Gegeben sei ein Kugelsektor, von welchem die Werte folgender Größen bekannt sind:
Radius der Kugel: r = 3
Höhe: h = 1,5
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach Auswahl des Tabelleneintrags Kugelsektor, der Eingabe der Werte für den Radius r der Kugel sowie für die Höhe h des Kugelsektors und einer Bedienung der Schaltfläche Berechnen gibt das Programm aus:
Mantelfläche Am: 28,274 FE
Schnittfläche As: 21,206 FE
Gesamtoberfläche Ao: 52,761 FE
Abschnittradius rho: 2,598
Umfang der Kugel U: 18,85
Volumen des Kugelsektors V: 28,274 VE
Koordinaten des Schwerpunkts des Kugelsektors: S (0 / 0 / 1,688)
Beispiel 4 - Kugelschicht:
Gegeben sei eine Kugelschicht, von welcher die Werte folgender Größen bekannt sind:
Radius der Kugel: r = 3
Höhe h1 = 2
Höhe h2 = 0,5
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach Auswahl des Tabelleneintrags Kugelschicht, der Eingabe der Werte für den Radius r der Kugel sowie für die Höhen h1 und h2 der Kugelschicht und einer Bedienung der Schaltfläche Berechnen ermittelt das Programm:
Höhe der Kugelschicht h: 1,5
Radius des oberen Schnittkreises r1: 2,236
Radius des unteren Schnittkreises r2: 2,958
Schnittfläche oben A1: 15,708 FE
Schnittfläche unten A2: 27,489 FE
Mantelfläche der Kugelschicht Am: 28,274 FE
Gesamtoberfläche der Kugelschicht Ao: 71,471 FE
Umfang der Kugel U: 18,85
Volumen der Kugelschicht V: 34,165 VE
Koordinaten des Schwerpunkts der Kugelschicht: S (0 / 0 / 1,185)
Beispiel 5 - Zylinder:
Gegeben sei ein Zylinder, von welchem die Werte folgender Größen bekannt sind:
Radius des Zylinders: r = 2
Höhe: h = 8
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach Auswahl des Tabelleneintrags Zylinder, der Eingabe der Werte für den Radius r des Zylinders sowie für die Höhe h dessen und einer Bedienung der Schaltfläche Berechnen gibt das Programm aus:
Umfang des Zylinders U (Zylinderumfang): 12,566
Grundfläche des Zylinders Ag: 12,566 FE
Mantelfläche des Zylinders Am: 100,531 FE
Gesamtoberfläche des Zylinders Ao (Zylinderoberfläche): 125,664 FE
Volumen des Zylinders V (Zylindervolumen): 100,531 VE
Koordinaten des Schwerpunkts des Zylinders: S (0 / 0 / 0)
Beispiel 6 - Hohlzylinder:
Gegeben sei ein Hohlzylinder, von welchem die Werte folgender Größen bekannt sind:
Außenradius des Hohlzylinders: r1 = 2
Innenradius des Hohlzylinders: r2 = 1,5
Höhe des Hohlzylinders: h = 7
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach Auswahl des Tabelleneintrags Hohlzylinder, der Eingabe der Werte für den Außenradius r1, den Innenradius r2 sowie für die Höhe h des Hohlzylinders und einer Bedienung der Schaltfläche Berechnen ermittelt das Programm:
Umfang des Innenzylinders Ui: 9,425
Umfang des Außenzylinders Ua: 12,566
Mantelfläche des Innenzylinders Mi: 65,973 FE
Mantelfläche des Außenzylinders Ma: 87,965 FE
Boden- bzw. Deckfläche Ab: 5,498 FE
Gesamtoberfläche des Hohlzylinders Ao: 164,934 FE
Mittlerer Radius rm: 0,25
Wanddicke des Hohlzylinders w: 0,5
Volumen des Hohlzylinders V: 38,485 VE
Koordinaten des Schwerpunkts des Hohlzylinders: S (0 / 0 / 0)
Beispiel 7 - Kegel (Kreiskegel):
Gegeben sei ein Kegel, von welchem die Werte folgender Größen bekannt sind:
Radius des Kreises der Bodenfläche: r = 2
Höhe des Kegels: h = 3
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach Auswahl des Tabelleneintrags Kegel, der Eingabe der Werte für den Radius des Kreises der Bodenfläche r des Kegels sowie für dessen Höhe h und einer Bedienung der Schaltfläche Berechnen gibt das Programm aus:
Mantelfläche des Kegels Am: 22,654 FE
Grundfläche des Kegels Ag: 12,566 FE
Gesamtoberfläche des Kegels Ao: 35,221 FE
Länge der Seitenlinie s: 3,606
Umfang des Grundkreises Uk: 12,566
Neigungswinkel der Seitenlinie des Kegels: 56,31°
Volumen des Kegels V: 12,566 VE
Koordinaten des Schwerpunkts des Kegels: S (0 / 0 / 0,75)
Beispiel 8 - Kegelstumpf:
Gegeben sei ein Kegelstumpf, von welchem die Werte folgender Größen bekannt sind:
Radius des Kreises der Deckfläche: r2 = 5
Radius des Kreises der Bodenfläche: r1 = 1
Höhe des Kegelstumpfes: h = 6
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach Auswahl des Tabelleneintrags Kegelstumpf, der Eingabe der Werte der o.a. Größen und einer Bedienung der Schaltfläche Berechnen ermittelt das Programm:
Fläche des Kreises der Bodenfläche A1: 78,54 FE
Fläche des Kreises der Deckfläche A2: 3,142 FE
Mantelfläche des Kegelstumpfs Am: 135,926 FE
Gesamtoberfläche des Kegelstumpfs Ao: 217,607 FE
Länge der Seitenlinie s: 7,211
Umfang des Kreises der Deckfläche Uo: 31,416
Umfang des Kreises der Bodenfläche Uu: 6,283
Neigungswinkel der Seitenlinie des Kegelstumpfs: 56,31°
Volumen des Kegelstumpfs V: 194,779 VE
Koordinaten des Schwerpunkts des Kegelstumpfs: S (0 / 0 / 1,839)
Beispiel 9 - Torus:
Gegeben sei ein Torus, von welchem die Werte folgender Größen bekannt sind:
Radius r1 = 1
Radius r2 = 3
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach Auswahl des Tabelleneintrags Torus, der Eingabe der Werte für die Radien r1 und r2 des Torus und einer Bedienung der Schaltfläche Berechnen gibt das Programm aus:
Oberfläche des Torus Ao: 118,435 FE
Umfang des Innenumkreises Ui: 12,566
Umfang des Außenumkreises Ua: 25,133
Volumen des Torus V: 59,218 VE
Koordinaten des Schwerpunkts des Torus: S (0 / 0 / 0)
Beispiel 10 - Schräg geschnittener Zylinder:
Gegeben sei ein schräg geschnittener Zylinder, von welchem die Werte folgender Größen bekannt sind:
Radius des Zylinders: r = 5
Höhe h1 = 2
Höhe h2 = 6
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach Auswahl des Tabelleneintrags Zylinder schräg. geschn., der Eingabe der o.a. Werte der zur Berechnung erforderlichen Größen und einer Bedienung der Schaltfläche Berechnen ermittelt das Programm:
Mantelfläche des schräg geschnittenen Zylinders Am: 125,664 FE
Grundfläche des Zylinders Au: 78,54 FE
(Schräg geschnittene) Deckfläche des Zylinders Ad: 84,59 FE
Gesamtoberfläche des schräg geschnittenen Zylinders Ao: 288,793 FE
Umfang des Zylinders U: 31,416
Neigungswinkel der Deckfläche des Zylinders: 20,832°
Volumen des schräg geschnittenen Zylinders V: 314,159 VE
Koordinaten des Schwerpunkts des schräg geschnittenen Zylinders: S (0 / 0 / 0,125)
Beispiel 11 - Doppelkegel I:
Gegeben sei ein Doppelkegel, von welchem die Werte folgender Größen bekannt sind:
Radius des Kegels: r = 5
Höhe des Doppelkegels: h = 12
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach Auswahl des Tabelleneintrags Doppelkegel I, der Eingabe der Werte für den Radius r des Kegels sowie für die Höhe h des Doppelkegels und einer Bedienung der Schaltfläche Berechnen gibt das Programm aus:
Mantelfläche des Doppelkegels Am: 408,407 FE
Länge der Seitenlinie des Doppelkegels s: 13
Umfang des Grundkreises des Doppelkegels U: 31,416
Neigungswinkel der Seitenlinie des Doppelkegels: 67,38°
Volumen des Doppelkegels V: 628,319 VE
Koordinaten des Schwerpunkts des Doppelkegels: S (0 / 0 / 0)
Beispiel 12 - Zylinderabschnitt:
Gegeben sei ein Zylinderabschnitt, von welchem die Werte folgender Größen bekannt sind:
Radius des Zylinders: r = 6
Höhe des Zylinderabschnitts: h = 8
Länge des Lots auf die Hufkante des Zylinderabschnitts: a = 9
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach Auswahl des Tabelleneintrags Zylinderabschnitt, der Eingabe der o.a. Werte der zur Berechnung erforderlichen Größen und einer Bedienung der Schaltfläche Berechnen ermittelt das Programm:
Hufkante b: 10,392
Horiz. Mittelpunktwinkel des Grundrisses: 120°
Volumen des Zylinderabschnitts V: 325,77 VE
Mantelfläche des Zylinderabschnitts M: 122,446 FE
Beispiel 13 - Schiefer Kegel:
Gegeben sei ein schiefer Kegel, von welchem die Werte folgender Größen bekannt sind:
Radius des Kreises der Bodenfläche: r = 5
Höhe des Kegels: h = 2
Koordinatenwerte des Mittelpunkts der Spitze des Kegels: K (2 / 3 / 2)
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach Auswahl des Tabelleneintrags Schiefer Kegel, der Eingabe der o.a. Werte der zur Berechnung erforderlichen Größen und einer Bedienung der Schaltfläche Berechnen gibt das Programm aus:
Mantelfläche des Kegels Am: 86,34 FE
Grundfläche des Kegels Ak: 78,54 FE
Gesamtoberfläche des Kegels Ao: 164,879 FE
Umfang des Grundkreises Uk: 31,416
Volumen des Kegels V: 52,36 VE
Koordinaten des Schwerpunkts des Kegels: S (0,5 / 0,75 / 0,5)
Beispiel 14 - Doppelkegel II:
Gegeben sei ein Doppelkegel, von welchem die Werte folgender Größen bekannt sind:
Oberer Radius des Doppelkegels: r1 = 2
Obere Höhe des Doppelkegels: h1 = 6
Unterer Radius des Doppelkegels: r2 = 1
Untere Höhe des Doppelkegels: h2 = 8
Es gilt, sich weitere wesentliche Eigenschaften dieses Gebildes ausgeben zu lassen.
Vorgehensweise und Lösung:
Nach Auswahl des Tabelleneintrags Doppelkegel II, der Eingabe der o.a. Werte der zur Berechnung erforderlichen Größen und einer Bedienung der Schaltfläche Berechnen ermittelt das Programm:
Mantelfläche des oberen Kegels Am: 79,477 FE
Länge der Seitenlinie des oberen Kegels s: 6,325
Umfang des Grundkreises des oberen Kegels Uk: 12,566
Neigungswinkel der Seitenlinie des oberen Kegels: 71,565°
Volumen des oberen Kegels V: 25,133 VE
Mantelfläche des unteren Kegels Am: 50,657 FE
Länge der Seitenlinie des unteren Kegels s: 8,062
Umfang des Grundkreises des unteren Kegels Uk: 6,283
Neigungswinkel der Seitenlinie des unteren Kegels: 82,875°
Volumen des unteren Kegels V: 8,378 VE

Grafische Darstellung - Beispiel 15 - Kugel

Grafische Darstellung - Beispiel 16 - Kugel durch 4 Punkte

Grafische Darstellung - Beispiel 17 - Kugelsegment geschnitten

Grafische Darstellung - Beispiel 18 - Kugelsegment

Grafische Darstellung - Beispiel 19 - Kugelsektor geschnitten

Grafische Darstellung - Beispiel 20 - Kugelsektor

Grafische Darstellung - Beispiel 21 - Kugelschicht geschnitten

Grafische Darstellung - Beispiel 22 - Kugelschicht

Grafische Darstellung - Beispiel 23 - Zylinder geschnitten

Grafische Darstellung - Beispiel 24 - Zylinder

Grafische Darstellung - Beispiel 25 - Hohlzylinder

Grafische Darstellung - Beispiel 26 - Hohlzylinder geschnitten

Grafische Darstellung - Beispiel 27 - Schräg geschnittener Zylinder

Grafische Darstellung - Beispiel 28 - Schräg geschnittener Zylinder

Grafische Darstellung - Beispiel 29 - Zylinderabschnitt

Grafische Darstellung - Beispiel 30 - Zylinderabschnitt

Grafische Darstellung - Beispiel 31 - Kegel geschnitten

Grafische Darstellung - Beispiel 32 - Kegel

Grafische Darstellung - Beispiel 33 - Torus geschnitten

Grafische Darstellung - Beispiel 34 - Torus geschnitten

Grafische Darstellung - Beispiel 35 - Schiefer Kegel

Grafische Darstellung - Beispiel 36 - Schiefer Kegel geschnitten

Grafische Darstellung - Beispiel 37 - Doppelkegel

Grafische Darstellung - Beispiel 38 - Doppelkegel geschnitten

Grafische Darstellung - Beispiel 39 - Doppelkegel

Grafische Darstellung - Beispiel 40 - Doppelkegel
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Grafikprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Üben sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema der Mathematik. Durch seine einfache interaktive Benutzbarbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Übungen hierzu. Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens genutzt werden.
Oftmals lassen sich hiermit auch die Lösungen von Mathe-Übungsaufgaben durch benutzerdefinierte Festlegungen und Eingaben numerisch oder grafisch ermitteln bzw. auswerten. Erlernte Fertigkeiten können somit auf anschauliche Weise untersucht werden. Implementierte Beispiele zu Sachverhalten erlauben die Bezugnahme zum entsprechenden Fachthemengebiet.
Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung oder einem mathematischen Beweis zu folgen.
Mittels der anschaulichen Gestaltung und leichten Bedienbarbarkeit der einzelnen Module dieser Software werden oftmals häufig gestellte Fragen mit den Anfangsworten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? zum entsprechenden Themengebiet auf verständliche Weise beantwortet und einfach erklärt sich durch dessen Benutzung vieles von alleine. Zudem liefert diese Applikation zu vielen gestellten Fragen eine verständliche Antwort, Beschreibung und Erklärung.
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.
Wikipedia - Zylinder
Wikipedia - Kegel
Wikipedia - Kugel
Wikipedia - Kugelschicht
Wikipedia - Kugelausschnitt
Wikipedia - Kugelsegment
Hinweise und Bilder zu Abwicklungen verschiedener Körper dieser Art (Kegel, Kugel, Zylinder) sind unter anderem auf der Seite Abwicklung zu erhalten.
Achsenabschnittsform einer Geraden - Punkt-Richtungs-Form einer Geraden - Zwei-Punkte-Form einer Geraden - Hessesche Normalenform einer Geraden - Allgemeine Form einer Gerade - Gerade - Gerade - Gerade - Gerade - Interaktiv - Gerade - Punkt - Gerade - Punkt - Interaktiv - Geradensteigung - Kreis - Punkt - Kreis - Punkt - Interaktiv - Kreis - Gerade - Kreis - Gerade - Interaktiv - Kreis - Kreis - Kreis - Kreis - Interaktiv - Kreisausschnitt - Kreissegment - Kreisring - Ellipse - Regelmäßiges Vieleck - Viereck - Allgemeines Viereck – Interaktiv - Satz des Ptolemäus - Satz des Arbelos - Pappus-Kreise - Archimedische Kreise - Hippokrates Möndchen - Varignon-Parallelogramm - Rechteck-Scherung - Soddy-Kreise - Polygone - Bewegungen in der Ebene - Affine Abbildung - Analyse affiner Abbildungen - Inversion einer Geraden am Kreis - Inversion eines Kreises am Kreis - Spirolateralkurven - Spiralen im Vieleck - Granvillesche Kurven - Bérard-Kurven - Eikurven - Kegelschnitt - Prinzip - Pyramidenschnitt - Prinzip - Kegelschnitte in Mittelpunktlage - Kegelschnitte in Mittelpunktlage - Interaktiv - Kegelschnitte in achsparalleler Lage - Kegelschnitte in achsparalleler Lage - Interaktiv - Kegelschnitte in Mittelpunktlage - Punkt - Kegelschnitte in Mittelpunktlage - Gerade - Allgemeine Kegelschnitte - Kegelschnitte durch 5 Punkte - Interaktive Geometrie mit Objekten - Winkelmaße - Strahlensatz - Teilungsverhältnis - Konstruktion einer Mittelsenkrechten - Konvexe Hülle - Dreieck - Pyramide - Quader im Raum (3D) - Ebenflächig und krummflächig begrenzte Körper (3D) - Platonische Körper (3D) - Archimedische Körper (3D) - Spezielle Polyeder (3D) - Selfbuild - Punkte (3D) - Selfbuild - Strecken (3D)
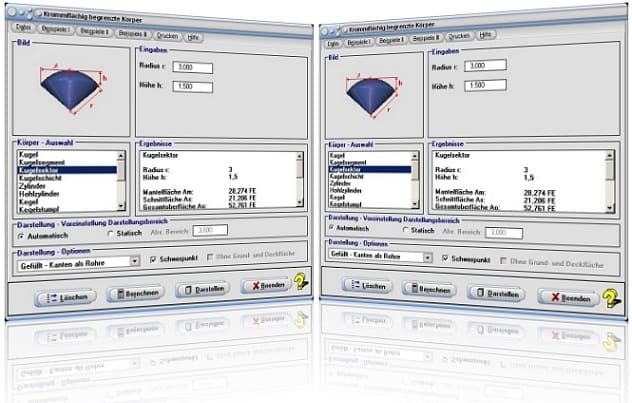
Startfenster des Unterprogramms Krummflächig begrenzte Körper
MathProf 5.0 - Startfenster des Unterprogramms Eben- und krummflächig begrenzte Körper

MathProf 5.0 - Grafikfenster des Unterprogramms Kurven von Funktionen in Parameterform

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung

SimPlot 1.0 - Grafik- und Animationsprogramm für unterschiedlichste Anwendungszwecke
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.
Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

















