MathProf - Kreise - Schnittpunkt - Berührpunkt - Chordale

Modul Kreis - Kreis

---

Das Modul [Geometrie] -[ Kreis] - Kreis - Kreis bietet die Möglichkeit, Untersuchungen und Kreisberechnungen mit Gleichungen von Kreisen verschiedener Definitionsformen durchzuführen.

 

Kreise können in diesem Unterprogramm in einer der nachfolgend aufgeführten Formen (Kreisgleichungen) definiert werden:

1. Kreisgleichung in Mittelpunktform (allgemeine Kreisgleichung):

Die Kreisgleichung in Mittelpunktform (Allgemeine Kreisgleichung) ist durch die Gleichnung (x - x_m)² + (y - y_m)² = r² definiert. Sie beschreibt einen Kreis mit dem Mittelpunkt x_m;y_m sowie dem Radius r und kann mit Hilfe des Satz des Pythagoras hergeleitet werden.

Hierbei sind:

r: Radius des Kreises
x_m,y_m: Koordinaten des Mittelpunkts des Kreises


2. Kreis in 3-Punkte-Form (Kreis durch 3 Punkte):

Ein Kreis in 3-Punkte-Form wird durch den Verlauf seiner Begrenzungslinie durch die drei Punkte P1 (x1;y1), P2 (x2;y2) und P3 (x3;y3) bestimmt.


3. Vektorielle Form (Vektorgleichung - Vektorform) des Kreises:

Die vektorielle Form einer Kreisgleichung lautet:



Sie wird durch den Ortsvektor des Mittelpunktes x₀;y₀ des Kreises gebildet. Der Radius des Kreises trägt die Bezeichnung r.


4. Kreisgleichung in Koordinatenform:

Ein Kreis kann durch eine implizite Gleichung in nachfolgend gezeigter Form beschrieben werden:

x²+y²+a·x+b·y+c = 0

Hierbei sind:

a,b,c: Reellwertige Koeffizienten


5. Kreisgleichung in Parameterform (Parameterdarstellung):

Die Defintion eines Kreises in Parameterdarstellung besitzt die nachfolgend dargestellte Form:

x = r·cos(k)+x₀
y = r·sin(k)+y₀

Hierbei sind:

r: Radius des Kreises
x₀,y₀: Koordinaten des Mittelpunkts des Kreises
k: Parameterwert (Winkel des Kreises) 0 ≤ k ≤ 2π


6. Scheitelgleichung des Kreises:

Die Scheitelgleichung eines Kreises lautet:

y² = 2·r·x-x²

r: Radius des Kreises

---

Bei der Durchführung von Untersuchungen in diesem Modul werden u.a. folgende Ergebnisse ermittelt und ausgegeben:
 

• Wesentliche Eigenschaften eines Kreises
• Schnittpunkte der Kreise
• Tangenten und Normalen in Schnittpunkten der Kreise
• Chordale der Kreise

 

Berechnung und Darstellung

 

 
Gehen Sie folgendermaßen vor, um Analysen mit Kreisen vorzunehmen:
 

1. Benutzen Sie die linksseitig positionierte Auswahlbox, um die Definitionsform des Kreises K1 auszuwählen und die rechtsseitig positionierte Auswahlbox, um die Definitionsform des Kreises K2 festzulegen.
    
2. Geben Sie die Werte für die entsprechenden Größen der Kreise K1 und K2 in die dafür zur Verfügung stehenden Felder ein:
   
   Kreis in Mittelpunktform: Koordinatenwerte des Mittelpunkts M und Wert für r²
   Kreis in 3-Punkte-Form: Koordinatenwerte der Punkte P1, P2 und P3
   Kreis in vektorieller Form: Koordinatenwerte x₀ und y₀ des Mittelpunkts und Parameter r²
   Kreis in Koordinatenform: Werte der Gleichungskoeffizienten a, b und c
   Kreis in Parameterform: Radius r, sowie Koordinatenwerte für x₀ und y₀
   Kreis in Scheitelgleichungsform: Radius r
    
3. Klicken Sie auf die Schaltfläche Berechnen, so gibt das Programm die ermittelten Ergebnisse aus.
    
4. Um sich die Zusammenhänge grafisch darstellen zu lassen, bedienen Sie die Schaltfläche Darstellen.

 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

Bedienformular

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:

• Tangenten: Darstellung der Tangenten des Kreises K2 in Schnittpunkten (falls vorhanden) ein-/ausschalten
• Normalen: Darstellung der Normalen des Kreises K2 in Schnittpunkten (falls vorhanden) ein-/ausschalten
• Chordale: Darstellung der Chordale der beiden Kreise ein-/ausschalten
• Punkte: Kennzeichnung markanter Punkte ein-/ausschalten
• Beschriftung: Beschriftung markanter Punkte ein-/ausschalten
• Koordinaten: Koordinatenwertanzeige markanter Punkte ein-/ausschalten

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Kreis – Kreis - Interaktiv Kreis - Punkt Kreis - Punkt - Interaktiv Kreis - Gerade Kreis - Gerade - Interaktiv

 

 
Beispiel 1:

Ein Kreis K1 sei durch die Gleichung X² + Y² + 1·X - 7·Y + 1 = 0 beschrieben. Von einem zweiten Kreis K2 sei bekannt, dass dieser seinen Mittelpunkt in M (3 / 3) sowie einen Radius r = 4 besitzt. Es gilt, die Schnittpunkte dieser, sowie die Tangenten und die Normalen des Kreises K2 in diesen Schnittpunkten ermitteln zu lassen.

Vorgehensweise und Lösung:

Wählen Sie den Eintrag Koordinatenform aus der linksseitig positionierten Auswahlbox und den Eintrag Mittelpunktform aus der rechtsseitig positionierten Auswahlbox, da Kreis K2 durch die Gleichung (x-x_m)²+(y-y_m)² = r² beschrieben werden kann.

Definieren Sie in den Eingabefeldern für Kreis K1 die Koeffizientenwerte a = 1, b = -7 und c = 1. Geben Sie in die Felder für Kreis K2 die Werte für x₀ = 3, y₀ = 3 ein. Das Feld mit der Bezeichnung r² erhält den Wert 4.

Nach einer Bedienung der Schaltfläche Berechnen gibt das Programm aus:

Für Kreis K1:

 

Gleichung in Mittelpunktform: (X+0,5)² + (Y-3,5)² = 3,391²

Mittelpunkt: M1 (-0,5 / 3,5)
Radius: r = 3,391
Fläche (Flächeninhalt): A = 36,128 FE
Umfang: U = 21,307

 

Für Kreis K2:

 

Gleichung in Mittelpunktform: (X-3)² + (Y-3)² = 4²

Mittelpunkt: M2 (3 / 3)
Radius: r = 4
Fläche (Flächeninhalt): A = 50,265 FE
Umfang: U = 25,133
 

Schnittpunkte beider Kreise:

 

Schnittpunkt 1: S1 (1,072 / 6,505)
Schnittpunkt 2: S2 (0,168 / 0,175)

Sehnenlänge des Kreisabschnitts S1S2: 6,394

 

Gleichung der Chordale der beiden Kreise: Y = 7·X-1

 

Gleichungen der Tangenten an Kreis K2 in den Schnittpunkten S1 und S2:

 

Tangente 1: Y = -0,523·X + 7,066
Tangente 2: Y = 0,201·X + 0,142
 

Gleichungen der Normalen des Kreises K2 in den Schnittpunkten S1 und S2:

 

Normale 1: Y = 1,911·X + 4,456
Normale 2: Y = -4,978·X + 1,011

Beispiel 2:

Ein Kreis sei durch die Scheitelgleichung Y² = 2·5·X - X² definiert. Ein zweiter sei durch die drei auf seiner Peripherie liegenden Punkte A (6 / -5), B (3 / 4) und C (-3 / 1) definiert. Es ist die Chordale dieser Kreise zu ermitteln. Zudem sind die Tangenten, sowie die Normalen des Kreises K2 in den Schnittpunkten der beiden Kreise auszugeben.

Vorgehensweise und Lösung:

Wählen Sie den Eintrag Scheitelgleichung aus der linksseitig positionierten Auswahlbox, sowie den Eintrag 3-Punkte-Form aus der rechtsseitig positionierten Auswahlbox.

Definieren Sie im Eingabefeld für Kreis K1 den Wert r = 5, in den Feldern für Kreis K2 die Koordinatenwerte für die Punkte A, B und C.

Führen Sie einen Klick auf die Schaltfläche Berechnen aus, so ermittelt das Programm:

Für Kreis K1:

 

Gleichung in Mittelpunktform: (X-5)² + Y² = 5²

Mittelpunkt: M1 (5 / 0)
Radius: r = 5
Fläche (Flächeninhalt): A = 78,54 FE
Umfang: U = 31,416

 

Für Kreis K2:

 

Gleichung in Mittelpunktform: (X-1,929)² + (Y+1,357)² = 5,463²

Mittelpunkt: M2 (1,929 / -1,357)
Radius: r = 5,463
Fläche (Flächeninhalt): A = 93,767 FE
Umfang: U = 34,327

 

Schnittpunkte beider Kreise:

 

Schnittpunkt 1: S1 (2,141 / 4,102)
Schnittpunkt 2: S2 (6,108 / -4,876)

Sehnenlänge des Kreisabschnitts S1S2: 9,815

 

Gleichung der Chordale der beiden Kreise: Y = -2,263·X + 8,948

 

Gleichungen der Tangenten an Kreis K2 in den Schnittpunkten S1 und S2:

 

Tangente 1: Y = 0,697·X + 2,61
Tangente 2: Y = 0,227·X - 6,264
 

Gleichungen der Normalen des Kreises K2 in den Schnittpunkten S1 und S2:

 

Normale 1: Y = -1,435·X + 7,175
Normale 2: Y = -4,399·X + 21,997
 
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3


Grafische Darstellung - Beispiel 4


Grafische Darstellung - Beispiel 5

   

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
 

 

Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.

Wikipedia - Kreis
Wikipedia - Kreistangente
Wikipedia - Pol und Polare

 

 

Achsenabschnittsform einer Geraden - Punkt-Richtungs-Form einer Geraden - Zwei-Punkte-Form einer Geraden - Hessesche Normalenform einer Geraden - Allgemeine Form einer Gerade - Gerade - Gerade - Gerade - Gerade - Interaktiv - Gerade - Punkt - Gerade - Punkt - Interaktiv - Geradensteigung - Kreis - Punkt - Kreis - Punkt - Interaktiv - Kreis - Gerade - Kreis - Gerade - Interaktiv - Kreis - Kreis - Interaktiv - Kreisausschnitt - Kreissegment - Kreisring - Ellipse - Regelmäßiges Vieleck - Viereck - Allgemeines Viereck – Interaktiv - Satz des Ptolemäus - Satz des Arbelos - Pappus-Kreise - Archimedische Kreise - Hippokrates Möndchen - Varignon-Parallelogramm - Rechteck-Scherung - Soddy-Kreise - Polygone - Bewegungen in der Ebene - Affine Abbildung - Analyse affiner Abbildungen - Inversion einer Geraden am Kreis - Inversion eines Kreises am Kreis - Spirolateralkurven - Spiralen im Vieleck - Granvillesche Kurven - Bérard-Kurven - Eikurven - Kegelschnitt - Prinzip - Pyramidenschnitt - Prinzip - Kegelschnitte in Mittelpunktlage - Kegelschnitte in Mittelpunktlage - Interaktiv - Kegelschnitte in achsparalleler Lage - Kegelschnitte in achsparalleler Lage - Interaktiv - Kegelschnitte in Mittelpunktlage - Punkt - Kegelschnitte in Mittelpunktlage - Gerade - Allgemeine Kegelschnitte - Kegelschnitte durch 5 Punkte - Interaktive Geometrie mit Objekten - Winkelmaße - Strahlensatz - Teilungsverhältnis - Konstruktion einer Mittelsenkrechten - Konvexe Hülle - Dreieck - Pyramide - Quader im Raum (3D) - Krummflächig begrenzte Körper (3D) - Ebenflächig und krummflächig begrenzte Körper (3D) - Platonische Körper (3D) - Archimedische Körper (3D) - Spezielle Polyeder (3D) - Selfbuild - Punkte (3D) - Selfbuild - Strecken (3D)
 

 

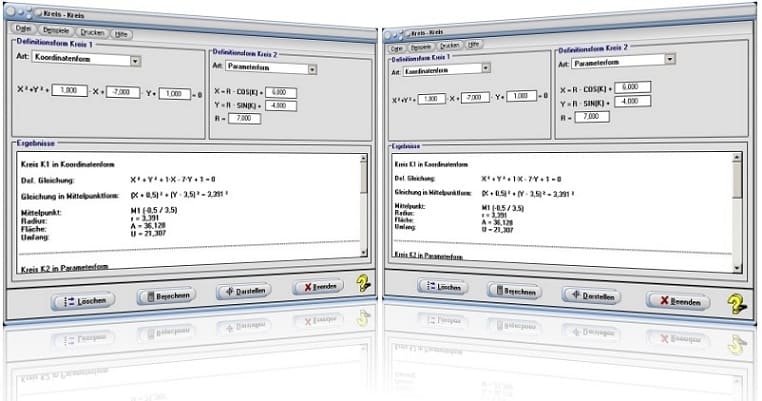
Startfenster des Unterprogramms Kreis-Kreis
 

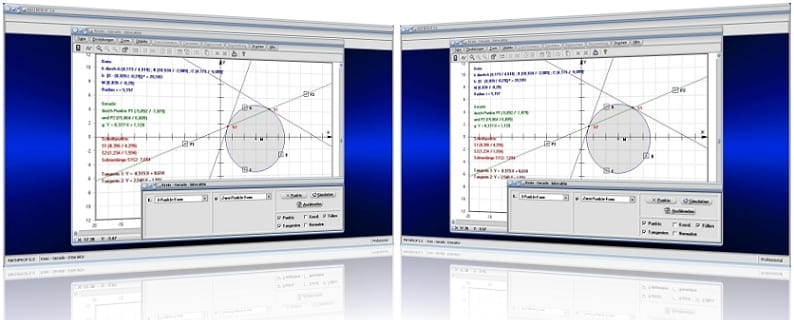
MathProf 5.0 - Unterprogramm Kreis-Gerade - Interaktiv

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---