MathProf - Kegelschnitte - 5 Punkte - Parabeln - Ellipsen - Hyperbeln

 

Modul Kegelschnitte durch 5 Punkte

---

 
Das Unterprogramm [Geometrie] - [Allgemeine Kegelschnitte] - Kegelschnitte durch 5 Punkte ermöglicht die Durchführung von Analysen und die Darstellung von Kegelschnitten, die durch 5 Punkte beschrieben werden.

 

 

Die allgemeine Gleichung eines Kegelschnitts besitzt die Form:

 

ax² + 2bxy + cy² + 2dx + 2ey + f = 0

 

a, b, c, d, e und f sind beliebige reelle Koeffizienten. Ein Kegelschnitt entsteht beim Schnitt eines geraden Kreiskegels mit dem Neigungswinkel α der Mantellinie durch eine Ebene, welche den Neigungswinkel β besitzt.

 

Ellipse: 0 ≤  b < α

Parabel: α = β

Hyperbel: π/2 ≥ b  > α

 

Beim Schnitt durch die Kegelspitze entstehen Punkt, Geradenpaar und Gerade.

                                                              

Durch eine Drehung des Koordinatensystems mit der Koordinatentransformation (Hauptachsentransformation)

 

 x = x' cos(α) - y' sin(α)                      

 y = y' sin(α) + y' cos(α)

 

lässt sich für eine geeignete Winkelgröße a stets erreichen, dass das gemischt-quadratische Glied x'·y' entfällt. Für a = c muss α = 45° gewählt werden. Ist a ≠ c muss a so gewählt werden, dass 2a = 2b / (a - c). Hierdurch entsteht für den Kegelschnitt die transformierte allgemeine Form:

 

ax² + cy² + 2dx + 2ey + f = 0

 

bei a ≠ 0 und c ≠ 0 mit n = d²/a + e²/c - f:

 

n > 0	a > 0, c > 0	Ellipse
n > 0	a < 0, c < 0	imaginär
n > 0	a · c < 0	Hyperbel
n = 0	a · c > 0	Punkt
n = 0	a · c < 0	Paar sich schneidender Geraden
n < 0	a > 0, c > 0	imaginär
n < 0	a < 0, c < 0	Ellipse
n < 0	a · c < 0	Hyperbel

 

bei a = 0 oder c = 0:

 

a = 0, c ≠ 0	d ≠ 0	Parabel
a = 0, c ≠ 0	d = 0	Paar zusammenfallender paralleler Geraden wenn e² - fc = 0
a ≠ 0, c = 0	e ≠ 0	Parabel
a ≠ 0, c = 0	e = 0	Paar zusammenfallender paralleler Geraden wenn d² - fa = 0
a = 0, c = 0	d ≠ 0, e ≠ 0	Gerade
a = 0, c = 0	d = 0, e ≠ 0	Parallele zur x-Achse
a = 0, c = 0	d ≠ 0, e = 0	Parallele zur y-Achse
a = 0, c = 0	d = 0, e = 0	imaginär

 

---

Satz von Pascal:

Im Sehnensechseck eines Kegelschnitts liegen die Schnittpunkte je zweier Gegenseiten auf einer Gerade.

Gemäß diesem Satz lässt sich auf umgekehrte Weise aus fünf gegebenen Punkte eine Ellipse konstruieren. In diesem Unterprogramm können Kegelschnitte (Kurven 2. Ordnung) untersucht werden, die durch 5 Punkte beschrieben werden. Aus den eingegebenen Punktkoordinaten ermittelt das Programm zunächst die Koeffizienten a, b, c, d, e und f der Ausgangsgleichung ax² + 2bxy + cy² + 2dx + 2ey + f = 0. Hiernach führt es Berechnungen mit diesem Kegelschnitt durch und ermittelt u.a.:

 

• Art des Kegelschnitts (entartet, nichtentartet)

• Koeffizienten der transformierten (hauptachsentransformierten) Gleichung des Typs ax² + cy² + 2dx + 2ey + f = 0

• Eigenschaften des Kegelschnitts

• Tangenten und Normalen bei best. Abszissenpos.

  

Das Programm gibt die Werte folgender Eigenschaften derartiger Kegelschnitte aus:
 

Hyperbel:

Allgemeine Eigenschaften des Kegelschnitts:

• Kegelwinkel
• Ortskoordinaten des Mittelpunkts M
• Halbachsen a und b
• Lineare Exzentrizität e und numerische Exzentrizität e
• Parameter 2p
• Ortskoordinaten der Brennpunkte B1 und B2
• Gleichungen der Asymptoten

 Eigenschaften des Kegelschnitts (der Kurve 2. Ordnung) an untersuchter Stelle (nur bei graf. Darstellung):

• Koordinatenwerte der Punkte an U-Stelle
• Gleichungen der Tangenten
• Gleichungen der Normalen
• Länge der Brennstrahlen

 

Ellipse (Kreis):

Allgemeine Eigenschaften des Kegelschnitts:

• Kegelwinkel
• Ortskoordinaten des Mittelpunkts M
• Halbachsen a und b
• Lineare Exzentrizität e und numerische Exzentrizität e
• Parameter 2p
• Ortskoordinaten der Brennpunkte B1 und B2

 Eigenschaften des Kegelschnitts an untersuchter Stelle (nur bei graf. Darstellung):

• Koordinatenwerte der Punkte an U-Stelle
• Gleichungen der Tangenten
• Gleichungen der Normalen
• Länge der Brennstrahlen

 

Parabel:

Allgemeine Eigenschaften des Kegelschnitts (nur bei graf. Darstellung):

• Kegelwinkel
• Ortskoordinaten des Scheitelpunkts S
• Ortskoordinaten des Brennpunkts B
• Numerische Exzentrizität e
• Parameter 2p
• Brennpunkt B

 Eigenschaften des Kegelschnitts an untersuchter Stelle:

• Koordinatenwerte der Punkte an U-Stelle
• Gleichungen der Tangenten
• Gleichungen der Normalen
• Länge der Brennstrahlen

 

 

 
Gehen Sie folgendermaßen vor, um Berechnungen mit Kegelschnitten dieser Art durchführen zu lassen und sich Zusammenhänge grafisch zu veranschaulichen:
 

1. Geben Sie die Koordinatenwerte der 5 Punkte ein, durch welche der Kegelschnitt verlaufen soll. Bedienen Sie ggf. zuvor die Taste Löschen.
    
2. Wird die Schaltfläche Berechnen bedient, so werden die ermittelten Ergebnisse in der Tabelle ausgegeben.
    
3. Soll bei der Ausgabe der grafischen Darstellung eine Untersuchung der Kurve an einer bestimmten Abszissenposition durchgeführt werden, so aktivieren Sie das Kontrollkästchen Analyse und legen durch die Eingabe des entsprechenden Werts im Formularbereich Analyse bei X = den entsprechenden Koordinatenwert fest, bei welchem diese durchgeführt werden soll.
    
4. Nach einer Benutzung der Schaltfläche Darstellen wird der entsprechende Kegelschnitt grafisch dargestellt.

Bei der Ausgabe der grafischen Darstellung werden folgende Bezeichnungskürzel verwendet:

B,B1,B2: Brennpunkt

M: Mittelpunkt

S: Scheitelpunkt

 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:

• Punkte: Kennzeichnung markanter Punkte des Kegelschnitts ein-/ausschalten
• Koordinaten: Koordinatenwertanzeige markanter Punkte des Kegelschnitts ein-/ausschalten
• Asymptoten: Darstellung von Asymptoten ein-/ausschalten (bei Hyperbeln)

Soll eine Untersuchung durchgeführt werden und wurde das Kontrollkästchen Analyse aktiviert, so stehen zudem folgende Kontrollkästchen zur Verfügung:

• Tangente(n): Darstellung der Tangente(n) des Kegelschnitts an U-Stelle ein-/ausschalten
• Normale(n): Darstellung der Normale(n) des Kegelschnitts an U-Stelle ein-/ausschalten
• Brennstrahl(en): Darstellung der Brennstrahlen an U-Stelle ein-/ausschalten

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Allgemeine Kegelschnitte

 

 

Beispiel 1 - Ellipse:

 

Werden die Koordinatenwerte für die 5 Punkte P1 (2 / -3), P2 (-4 / 1), P3 (3 / 6), P4 (4 / -2) und P5 (7 / 3) eingegeben, so ermittelt das Programm für den durch diese Punkte bestimmten Kegelschnitt, nach Eingabe der entsprechenden Koeffizientenwerte in die dafür vorgesehenen Felder und einer Bedienung der Schaltfläche Berechnen:

 

Gleichung dieses Kegelschnitts in allgemeiner Form:

-0,04x² + 0,029xy - 0,056y² + 0,075x + 0,104y + 1 = 0

 

Gleichung des Kegelschnitts in transformierter allgemeiner Form (nach durchgeführter Haupachsentransformation):

-0,031x² -0,064y² + 0,117x + 0,052y + 1 = 0

 

Für die Eigenschaften dieses Kegelschnitts gibt das Programm aus:

 

Typ: Ellipse

Kegelwinkel: 30,288°

Mittelpunkt des Kegelschnitts: M (1,418 / 1,299)

Halbachse a: 6

Halbachse b: 4,169

Lineare Exzentrizität e: 4,314

Numerische Exzentrizität ε: 0,719

Parameter 2p: 5,795

Brennpunkt: B1 (-2,308 / -0,877)

Brennpunkt: B2 (5,143 / 3,475)

 

Sind die Eigenschaften des Kegelschnitts an Stelle x = 4 zu untersuchen, so aktivieren Sie das Kontrollkästchen Analyse und geben diesen Wert in das dafür vorgesehene Feld ein. Werden nach einer Bedienung der Schaltfläche Darstellen die Kontrollkästchen Normale, Tangente sowie Brennstrahlen aktiviert, so gibt das Programm zusätzlich aus:

 

Koordinatenwerte der Kurve an untersuchter Stelle:

 

Punkt 1: TP1 (4 / 5,936)
Punkt 2: TP2 (4 / -2)

Tangente durch TP1: Y = -0,157·X+6,566
Tangente durch TP2: Y = 0,676·X-4,704

Normale durch TP1: Y = 6,356·X-19,486
Normale durch TP2: Y = -1,479·X+3,918

Länge Brennstrahl TP1-B1: 9,285
Länge Brennstrahl TP1-B2: 2,714

Länge Brennstrahl TP2-B1: 6,407
Länge Brennstrahl TP2-B2: 5,593

 

Beispiel 2 - Hyperbel:

 

Werden die Koordinatenwerte für die 5 Punkte P1 (5 / 1), P2 (3 / 1), P3 (4 / 3), P4 (4 / -4) und P5 (-1 / 3) eingegeben, so ermittelt das Programm, für den durch diese Punkte bestimmten Kegelschnitt, nach Eingabe der entsprechenden Koeffizientenwerte in die dafür vorgesehenen Felder und einer Bedienung der Schaltfläche Berechnen:

 

Gleichung dieses Kegelschnitts in allgemeiner Form:

0,04x² + 0,101xy + 0,004y² - 0,423x - 0,399y + 1 = 0

 

Gleichung des Kegelschnitts in transformierter allgemeiner Form (nach durchgeführter Haupachsentransformation):

0,076x² -0,031y² - 0,576x - 0,083y + 1 = 0

 

Für die Eigenschaften dieses Kegelschnitts gibt das Programm aus:

 

Typ: Hyperbel

Kegelwinkel: 35,101°

Mittelpunkt des Kegelschnitts: M (3,872 / 1,103)

Halbachse a: 0,724

Halbachse b: 1,125

Lineare Exzentrizität e: 1,337

Numerische Exzentrizität ε: 1,847

Parameter 2p: 3,494

Brennpunkt: B1 (2,778 / 0,333)

Brennpunkt: B2 (4,966 / 1,872)

 

Asymptote 1: Y = -24,593·X+96,323

Asymptote 2: Y = -0,407·X+2,677
 

Sind die Eigenschaften des Kegelschnitts an Stelle x = 4 zu untersuchen, so aktivieren Sie das Kontrollkästchen Analyse und geben diesen Wert in das dafür vorgesehene Feld ein. Werden nach einer Bedienung der Schaltfläche Darstellen die Kontrollkästchen Normale, Tangente sowie Brennstrahlen aktiviert, so gibt das Programm zusätzlich aus:

 

Koordinatenwerte der Kurve an untersuchter Stelle:

 

Punkt 1: TP1 (4 / 3)
Punkt 2: TP2 (4 / -4)

Tangente durch TP1: Y = -7,143·X+31,571
Tangente durch TP2: Y = -17,857·X+67,429

Normale durch TP1: Y = 0,14·X+2,44
Normale durch TP2: Y = 0,056·X-4,244

Länge Brennstrahl TP1-B1: 2,933
Länge Brennstrahl TP1-B2: 1,485

Länge Brennstrahl TP2-B1: 4,503
Länge Brennstrahl TP2-B2: 5,951
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3


Grafische Darstellung - Beispiel 4


Grafische Darstellung - Beispiel 5


Grafische Darstellung - Beispiel 6
 

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
 

 

Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.

Wikipedia - Kegelschnitte
Wikipedia - Hyperbel
Wikipedia - Ellipse
Wikipedia - Parabel
Wikipedia - Hauptachsentransformation
 

 

 

Achsenabschnittsform einer Geraden - Punkt-Richtungs-Form einer Geraden - Zwei-Punkte-Form einer Geraden - Hessesche Normalenform einer Geraden - Allgemeine Form einer Gerade - Gerade - Gerade - Gerade - Gerade - Interaktiv - Gerade - Punkt - Gerade - Punkt - Interaktiv - Geradensteigung - Kreis - Punkt - Kreis - Punkt - Interaktiv - Kreis - Gerade - Kreis - Gerade - Interaktiv - Kreis - Kreis - Kreis - Kreis - Interaktiv - Kreisausschnitt - Kreissegment - Kreisring - Ellipse - Regelmäßiges Vieleck - Viereck - Allgemeines Viereck – Interaktiv - Satz des Ptolemäus - Satz des Arbelos - Pappus-Kreise - Archimedische Kreise - Hippokrates Möndchen - Varignon-Parallelogramm - Rechteck-Scherung - Soddy-Kreise - Polygone - Bewegungen in der Ebene - Affine Abbildung - Analyse affiner Abbildungen - Inversion einer Geraden am Kreis - Inversion eines Kreises am Kreis - Spirolateralkurven - Spiralen im Vieleck - Granvillesche Kurven - Bérard-Kurven - Eikurven - Kegelschnitt - Prinzip - Pyramidenschnitt - Prinzip - Kegelschnitte in Mittelpunktlage - Kegelschnitte in Mittelpunktlage - Interaktiv - Kegelschnitte in achsparalleler Lage - Kegelschnitte in achsparalleler Lage - Interaktiv - Kegelschnitte in Mittelpunktlage - Punkt - Kegelschnitte in Mittelpunktlage - Gerade - Allgemeine Kegelschnitte - Interaktive Geometrie mit Objekten - Winkelmaße - Strahlensatz - Teilungsverhältnis - Konstruktion einer Mittelsenkrechten - Konvexe Hülle - Dreieck - Pyramide - Quader im Raum (3D) - Krummflächig begrenzte Körper (3D) - Ebenflächig und krummflächig begrenzte Körper (3D) - Platonische Körper (3D) - Archimedische Körper (3D) - Spezielle Polyeder (3D) - Selfbuild - Punkte (3D) - Selfbuild - Strecken (3D)

 

 

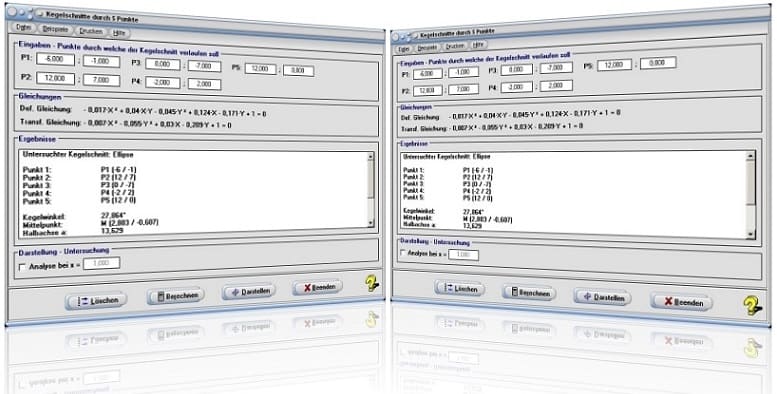
Startfenster des Unterprogramms Kegelschnitte durch 5 Punkte
 

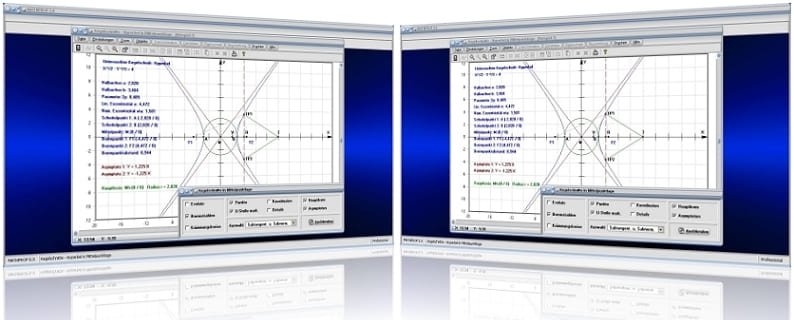
MathProf 5.0 - Unterprogramm Kegelschnitte in Mittelpunktlage

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---