MathProf - Funktionsgleichungen - Gleichung - Berechnen - Rechner

 

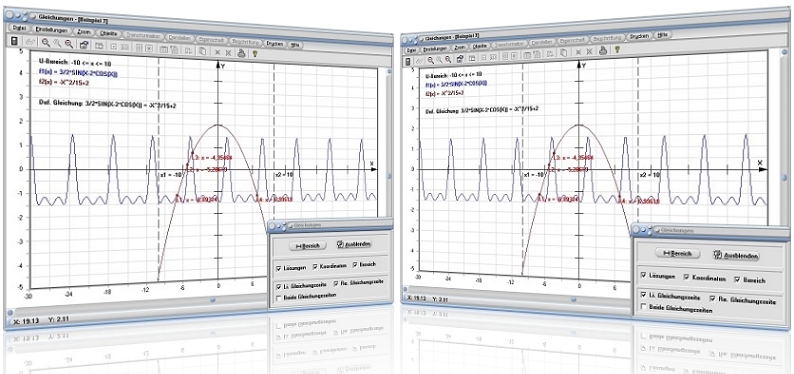
Modul Gleichungen

---

 
Mit Hilfe des Unterprogramms [Algebra] - Gleichungen lassen sich Lösungen von linearen und nichtlinearen Gleichungen, welche in explizit definierter Form vorliegen, numerisch ermitteln und Zusammenhänge zu diesem Thema grafisch analysieren.

 

 

Gleichungen sind mathematische Aussageformen, bei welchen zwei Terme durch Gleichheitszeichen miteinander verbunden sind. Diese beiden Terme werden als Linksterm und Rechtsterm bezeichnet. Gleichungen deren Terme keine Variablen enthalten sind Aussagen, welche weder wahr noch falsch sind. Der Definitionsbereich D einer Gleichung ist der Durchschnitt der Definitionsbereiche aller in ihr vorkommenden Terme, welche Variablen beinhalten. Ein Term ist ein Rechenausdruck, der theoretisch als Zahl berechnet werden kann. Um einen Termwert bestimmen zu können, werden dessen Variablen durch Zahlenwerte ersetzt. Beispielsweise ist der Term T(x) = 3x-1 derjenige Term bei welchem die Variable x durch eine Zahl ersetzt wird.

Eine Bestimmungsgleichung ist eine Gleichung, für welche eine oder mehrere Lösungen gesucht werden. Sie besitzt mindestens eine Variable (Unbekannte). Funktionsgleichungen sind keine Bestimmungsgleichungen. Eine Funktionsgleichung verfügt über mindestens zwei verschiedene Unbekannte.
 
Beispiel einer Bestimmungsgleichung: 2x+6 = 24
Beispiel einer Funktionsgleichung: y = 4x + 8




Dieses Modul ermöglicht die Durchführung einer iterativen Lösung von Funktionsgleichungen der Form f1(x) = f2(x), innerhalb eines frei wählbaren Untersuchungsbereichs.

Gleichungslösungen dieser Art sind grafisch als Abszissenkoordinatenwerte der Schnittpunkte der Kurven der links- und rechtsseitig definierten Gleichungsterme zu interpretieren.

 

 
Zur elementaren Algebra zählt unter anderem das Lösen von mathematischen Gleichungen. Hierbei werden neben den Grundrechenarten auch Berechnungen mit Variablen durchgeführt. Nachfolgend finden Sie Hinweise zu einigen Arten von Gleichungen. Für viele Gleichungen unterschiedlichster Form kann mit Hilfe dieses Moduls nach Lösungen gesucht werden.
 
Algebraische Gleichungen (Polynomiale Gleichungen) - Algebraische Funktionen:

Algebraische Gleichungen besitzen die Form a_n​xⁿ + a_n−1​xⁿ⁻¹ + … + a₁​x +a₀​ = 0. Zur Ermittlung der Lösungen von Gleichungen dieser Art dürfen lediglich algebraische Rechenoperationen (Addieren, Subtrahieren, Multiplizieren, Dividieren, Radizieren, Potenzieren) verwendet werden. Zu den algebraischen Gleichungen zählen quadratische Gleichungen, Wurzelgleichungen, Bruchgleichungen sowie lineare Gleichungen. Als algebraische Funktion wird die Funktion bezeichnet, welche als Lösung einer algebraischen Gleichung auftritt. Beispiele für algebraische Gleichungen sind 5x⁴ + 3x³ - 2x² + x = 0 und -7x⁵ - x³ - 2x² + 3 = 0.
 
Symmetrische Gleichungen - Symmetrische Funktionen:

Eine symmetrische Funktion ist eine Funktion mehrerer Variablen, bei welcher die Variablen untereinander vertauscht werden können, ohne den Wert dieser zu verändern. Mit einer symmetrischen Gleichung wird eine ganzrationale Gleichung (Polynom) bezeichnet, deren reelle Koeffizientenfolge symmetrisch ist.

Lineare Gleichungen:
 
Lineare Gleichungen sind Gleichungen bei welchen Gleichungsvariablen nur in erster Potenz auftreten. Im allgemeinen werden Variablen in Gleichungen mit der Variable x bezeichnet. Die allgemeine Form einer Gleichung dieser Art lautet a·x - b = 0. Beispiele für Gleichungen dieser Art sind 3x + 4 = 0 und -7x - 2 = 1.

Prinzipielle Vorgehensweise zum Lösen von Gleichungen dieser Art (Gleichungen nach x auflösen):

a·x + b = 0    | -b
a·x       = -b  | :a
x = -b/a

L = { -b/a}  mit a ≠ 0

Bei Bestimmung der Lösungen einer derartigen Gleichung gilt es auf die Grundmenge von a und b zu achten.
 
Wurzelgleichungen:
 
Bei Wurzelgleichungen handelt es sich um Gleichungen, bei welchen mindestens eine der Gleichungsvariablen mindestens einmal im Radikanden einer Wurzel auftritt. Beispiele für Wurzelgleichungen sind √x - 2 = 3 und √x² - 2 - √x - 1 = 0. Vor der Ermittlung der Lösungen einer Wurzelgleichung gilt es die zulässige Definitionsmenge zu bestimmen. Bei einer Quadratwurzel darf beispielsweise kein Radikand mit negativem Wert auftreten.
 
Bruchgleichungen:
 
Unter Bruchgleichungen werden Gleichungen verstanden, bei welchen sich mindestens einmal eine Variable in einem Nenner vorkommt. Die Vorgehensweise zur Lösung von Gleichungen dieser Art wird unter dem Fachthema Rechnen mit Brüchen beschrieben.

Exponentialgleichungen:

Eine Gleichung wird als Exponentialgleichung bezeichnet, wenn die Gleichungsvariable als Exponent auftritt. Die Lösung einer Gleichung der Form a^x = c heißt Logarithmus zur Basis zur Basis a und lautet: x = log_ac. Beispiele für Exponentialgleichungen sind 4^x = 5 und 3^2x = 6.

Logarithmusgleichungen  (Logarithmische Gleichungen):

Eine Gleichung wird als Logarithmusgleichung bezeichnet, wenn die Gleichungsvariable als Numerus eines Logarithmus auftritt, wie beispielsweise in der Form log_ax = b. Einfache Gleichungen dieser Art lassen sich durch Logarithmieren lösen. Dies geschieht, indem beide Seiten der Gleichung zur Basis des Logarithmus potenziert werden und hierauf entsprechende Logarithmen- und Potenzgesetze angewandt werden. Beispiele für Logarithmusgleichungen sind log₄x = 5 und lg(2x-1)-lg(x)=3.
 
Transzendente Gleichungen - Transzendente Funktionen:

Eine transzendente Funktion ist eine Funktion, die keine algebraische Funktion ist. Hierzu zählen u.a. Exponentialfunktionen, trigonometrische Funktionen sowie Logarithmusfunktionen. Eine transzendente Gleichung ist eine Gleichung, welche mindestens eine transzendente Funktion beinhaltet. Hierzu zählen auch trigonometrische (goniometrische) Gleichungen. Gleichungen dieser Art sind im allgemeinen nicht algebraisch lösbar. Beispiele für Gleichungen dieser Art sind e^x - 2 = x, sin(3x) + log(x) = -3x³ oder arcsin(x) - e^x = -1.

Homogene Gleichung - Inhomogene Gleichung:
 
Eine Gleichung wird als homogene Gleichung bezeichnet, wenn ihre rechte Seite gleich Null ist. Bei einer inhomogenen Gleichung befindet rechtsseitig sich keine Null.
 

 


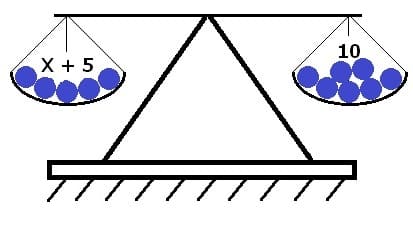
Mathematische Gleichungen können in Form des Modells einer Waage dargestellt werden. Die linke Gleichungsseite entspricht hierbei der linken Waagschale, die rechte Seite dieser der rechten Waagschale. Befindet sich diese Waage im Gleichgewicht, so entspricht der Wert des linken Terms derer dem des rechten Werts der Gleichung. Wird auf den Waagschalen die Wertigkeit derart geändert, dass die Waage im Gleichgewicht bleibt, so wird von einer Äquivalenz gesprochen.

Äquivalente Gleichungen (gleichwertige Gleichungen):

Zwei Gleichungen werden als äquivalent (gleichwertig) bezeichnet, wenn sie dieselben Definitionsbereiche sowie dieselben Lösungsmengen besitzen. Ist dies nicht der Fall, so sind sie nicht äquivalent.

Beispiele:
Die beiden Gleichungen x + 2 = 4 und x = 2 sind äquivalent und besitzen dieselbe Lösungsmenge L={2}.
Die beiden Gleichungen 4 = 1 und x² = -2 verfügen über ihre Grundmenge Q, über keine Lösung und sind aufgrund dessen äquivalent. Sie besitzen die Lösungsmenge L={}.
Die beiden Gleichungen x + 3 = 0 und (x + 3) (x - 3) = 0 sind nicht äquivalent, da sie unterschiedliche Lösungsmengen besitzen. Die Gleichung x + 3 = 0 besitzt die Lösungsmenge L={3}, die Gleichung (x + 3) (x - 3) = 0 besitzt die Lösungsmenge L={-3;3}

Äquivalenzumformung:

Gleichungen addieren / Gleichungen subtrahieren: Zwei Gleichungen bleiben äquivalent, wenn auf beiden Seiten dieselbe Zahl addiert oder subtrahiert wird (Additionsverfahren).
Gleichungen multiplizieren: Zwei Gleichungen bleiben äquivalent, wenn beide Seiten mit derselben Zahl multipliziert werden und diese Zahl nicht gleich 0 ist .
Gleichungen dividieren: Zwei Gleichungen bleiben äquivalent, wenn beide Seiten durch dieselbe Zahl dividiert werden und diese Zahl nicht gleich 0 ist.

Umstellung von Gleichungen (Formelumstellung):

Zur Umstellung von Gleichungen ist auf beiden Seiten dieselbe Rechenoperation (addieren, subtrahieren, dividieren, multiplizieren) durchzuführen. Bei Anwendung einer Division ist darauf zu achten, dass auf keiner der beiden Gleichungsseiten eine Division durch die Zahl 0 (Null) erfolgt.

Nachfolgend sind einige sehr einfache Beispiele aufgeführt, an welchen die oben beschriebenen und durchzuführenden Äquivalenzumformungen verdeutlicht werden sollen.

Beispiel 1:

Es gilt die einfache Gleichung 3 + x = 5 nach der Variable x zu lösen.

Um diese Gleichung nach der Variablen x aufzulösen, ist auf beiden ihrer Seiten die Zahl 3 zu subtrahieren.

3 + x = 5
3 + x = 5  |  -3

Es folgt:

x = 5 - 3
x = 2

Die Lösung dieser Gleichung lautet somit: x = 2.

Beispiel 2:

Es gilt die einfache Gleichung 4x = 20 nach der Variable x zu lösen.

Um diese Gleichung nach der Variablen x aufzulösen, sind beide ihrer Seiten durch die Zahl 4 zu dividieren.

4x = 20
4x = 20 | :4

Es folgt:

x = 20/4
x = 5

Die Lösung dieser Gleichung lautet somit: x = 5.

Beispiel 3:

Es gilt die einfache Gleichung x/3 =15 nach der Variable x zu lösen.

Um diese Gleichung nach der Variablen x aufzulösen, sind beide ihrer Seiten mit der Zahl 3 zu multiplizieren.

x/3 = 15
x/3 = 15 | ·3

Es folgt:

x = 45

Die Lösung dieser Gleichung lautet somit: x = 45.
 
      

 

Eine Ermittlung der numerischen und grafischen Lösungen von linearen und nichtlinearen Gleichungen (Durchführung einer Gleichungslösung) können Sie veranlassen, indem Sie Folgendes ausführen:

1. Geben Sie den, gemäß den geltenden Syntaxregeln formulierten, linken Gleichungsterm (linke Gleichungsseite) im Feld mit der Bezeichnung f1(x) = ein.
   
   Definieren Sie den rechten Funktionsgleichungsterm (rechte Gleichungsseite) im Feld mit der Bezeichnung f2(x) =. Beachten Sie auch hierbei die geltenden Syntaxregeln.
    
2. Legen Sie, durch die Eingabe von Zahlenwerten, den Untersuchungsbereich fest, über welchen die Ermittlung durchgeführt werden soll (Untersuchen in Bereich von x1 = und bis x2 =). (voreingestellt: -10 ≤ x ≤ 10)
    
3. Durch die Wahl des entsprechenden Kontrollschalters Grob, Mittel, Fein, Sehr fein bestimmen Sie die zu verwendende Untersuchungsgenauigkeit zur numerischen Ermittlung der Gleichungslösungen.
    
4. Nach einem Klick auf die Schaltfläche Berechnen werden die Ergebnisse ausgegeben.
    
5. Möchten Sie sich die Zusammenhänge grafisch veranschaulichen, so bedienen Sie hierauf die Schaltfläche Darstellen.
    

6. Wird das Kontrollkästchen Li. Gleichungsseite aktiviert, so wird die linksseitig definierte Funktion f1(x) ausgegeben. Wird das Kontrollkästchen Re. Gleichungsseite aktiviert, so stellt das Programm die rechtsseitig definierte Funktion f2(x) dar.
   
   Wenn Sie das Kontrollkästchen Beide Gleichungsseiten aktivieren, so wird (zusätzlich) die Funktion f(x) = f1(x) - f2(x) ausgegeben.
    

7. Möchten Sie einen neuen Untersuchungsbereich festlegen, so können Sie die Schaltfläche Bereich auf dem Bedienformular drücken und die entsprechenden Werte im daraufhin erscheinenden Formular eingeben. Übernommen werden diese, wenn Sie die sich dort befindende Schaltfläche Ok bedienen (je schmaler der Bereich gewählt wird, desto exakter sind die resultierenden Berechnungsergebnisse).

Hinweis:

Bei Ausgabe einer grafischen Darstellung werden ermittelte Gleichungslösungen mit der Bezeichnung L, sowie einem fortlaufenden Nummer-Index gekennzeichnet.
 

 
Zur Lösung von Textgleichungen ist es erforderlich, aus einem vorgegebenen Aufgabentext eine Gleichung mit einer Variablen zu formulieren.

Nachfolgend wird auf die prinzipielle Vorgehensweise zum Lösen von derartigen Gleichungen eingegangen und das zur Bearbeitung derartiger Aufgaben erforderliche Schema aufgezeigt:

- Textgleichung sorgfältig wiederholt durchlesen
- Markieren (hervorheben) relevanter Textstellen
- Herausfinden nach was gesucht wird
- Wenn möglich, grafische Skizze des vorliegenden Sachverhalts erstellen
- Analysieren und Erstellen der Formeln und Gesetze die zur Lösung des gestellten Problems führen
- Notwendige Gleichung aufstellen
- Lösen der aufgestellten Gleichung durch entsprechende Äquivalenzumformungen
- Kontrollieren der ermittelten Lösungen durch Einsetzen des Ergebnisses in die aufgestellte Gleichung
- Formulierung eines relevanten Antwortsatzes


Im Weiteren sind die Beispiele einiger einfacher Textgleichungen aufgeführt:

Beispiel 1:

Das Vierfache einer gesuchten Zahl ergibt 12. Wie lautet diese Zahl?

Umsetzung der formulierten Textaufgabe in eine mathematische Gleichung:

4 ⋅ x = 12

Lösen der Gleichung:

4x = 12 | :4
x = 3

Ergebnis:
Die gesuchte Zahl lautet 3.


Beispiel 2:

Das Doppelte einer Zahl vermehrt um 5 ergibt deren Gegenzahl vermindert um 2.

Umsetzung der formulierten Textaufgabe in eine mathematische Gleichung:

2⋅x + 5 = - x - 2

Lösen der Gleichung:

2x + 5 = - x - 2   | +x
3x + 5 =  - 2       | - 5
3x      = - 7        |  : 3
x      = - 7/3

Ergebnis:
Die gesuchte Zahl lautet -7/3.
 
 

 
Zu Aufgaben dieser Art zählen unter anderem Altersrätsel. Hierbei handelt es sich um Textgleichungen, bei denen das Alter zweier oder mehrerer Personen zu unterschiedlichen Zeiten miteinander in Verbindung gebracht wird.

Beispiel:

Eine Mutter ist heute 44, ihr Sohn ist 18 Jahre alt. In wie vielen Jahren wird die Mutter doppelt so alt wie ihr Sohn sein?

Lösungsansatz:

44 + x = 2·(18 + x)

Anzahl der gesuchten Jahre: x

Lösung der aufgestellten Gleichung:

44 + x = 2·(18 + x)
44 + x = 36 + 2x | - x
44 = 36 + x | -36
x = 8

Ergebnis:
in 8 Jahren wird ihr Sohn 18 + 8 = 26 Jahre alt sein. Die Mutter wird in 44 + 8 = 52 Jahre alt sein. Somit ist sie in 8 Jahren doppelt so alt wie ihr Sohn.

  

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Grafikprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Üben sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Übungen hierzu. Oftmals lassen sich hiermit auch die Lösungen von Übungsaufgaben durch benutzerdefinierte Festlegungen und Eingaben numerisch oder grafisch ermitteln bzw. auswerten. Erlernte Fertigkeiten können somit auf einfache Weise untersucht werden. Implementierte Beispiele zu Sachverhalten erlauben die Bezugnahme zum entsprechenden Fachthema.

 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:

• Lösungen: Markierung und Nummerierung gefundener Lösungen ein-/ausschalten
• Koordinaten: Anzeige der Koordinaten des gewählten Untersuchungsbereichs ein-/ausschalten
• Bereich: Markierung des gewählten Untersuchungsbereichs ein-/ausschalten

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Funktionsschnittpunkte

Gleichungen 2.- 4. Grades

Mathematische Funktionen I

 

Beispiel 1 - Berechnen und plotten der Lösungen einer Funktionsgleichung:

Es gilt, die Lösungen der Funktionsleichung x²+2·x = cos(x) mit der Variable x innerhalb eines Untersuchungsbereichs -10 ≤ x ≤ 10 ermitteln zu lassen.

Vorgehensweise und Lösung:

Nach der Definition des Terms X^2+2*X im linksseitig angeordneten Eingabefeld f1(x) = und der Einbindung des Terms COS(X) in das rechtsseitig angeordnete Feld f2(x) =, ermittelt das Programm nach einer Eingabe der Werte -10 und 10 zur Festlegung des Untersuchungsbereichs und einer Bedienung der Schaltfläche Berechnen folgende Ergebnisse:

Lösungen der Gleichung x²+2·x = cos(x):

X1 = -1,85072

X2 = -0,38772

 

Hinweis:

Bei Ausgabe der grafischen Darstellung wird bei einer Aktivierung des Kontrollkästchens Beide Gleichungsseiten zusätzlich die Funktionsgleichung f(x) = x²+2·x-cos(x) dargestellt, da nach einer Umstellung und Auflösung der Gleichung x²+2·x = cos(x) nach 0, die Gleichung x²+2·x-cos(x) = 0 resultiert.

 

Beispiel 2 - Berechnen und plotten der Lösungen einer Funktionsgleichung:

 

Es sind die Schnittpunkte einer Parabel f1(x) = x² (quadratische Gleichung) und einer Gerade f2(x) = x/4+1 (lineare Gleichung) zu ermitteln.

 

Vorgehensweise und Lösung:

 

Es ist der Term X^2 der Funktion f1(x) in einem der Eingabefelder zu definieren und der Term X/4+1 der Funktion f2(x) im zweiten. Nach einer Festlegung eines Untersuchungsbereichs -10 ≤ x ≤ 10 und einer Bedienung der Schaltfläche Berechnen gibt das Programm aus:

 

X1 = -0,88278

X2 = 1,13278

 

Durch Einsetzen der Lösungen x1 und x2 in einen der beiden Terme können die Y-Koordinatenwerte der Schnittpunkte der Parabel und der Gerade ermittelt werden. Es sind dies:

 

Y1 = 0,7793

Y2 = 1,2831

 

Es schneiden sich Parabel und Gerade in den Punkten S1 (0,88278 / 0,7793) und S2 (1,13278 / 1,2831)
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3


Grafische Darstellung - Beispiel 4


Grafische Darstellung - Beispiel 5


Grafische Darstellung - Beispiel 6


Grafische Darstellung - Beispiel 7


Grafische Darstellung - Beispiel 8

    
Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
 

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Gleichung zu finden.

 

Cramersche Regel - Matrizen - Lineares Gleichungssystem - Gauß'scher Algorithmus - Unterbestimmtes lineares Gleichungssystem - Überbestimmtes lineares Gleichungssystem - Komplexes Gleichungssystem - Lineare Optimierung - Grafische Methode - Lineare Optimierung - Simplex-Methode - Gleichungen 2.- 4. Grades - Ungleichungen - Prinzip - Spezielle Gleichungen - Richtungsfelder von DGL 1. Ordnung - Interaktiv - DGL 1. Ordnung (Differentialgleichungen) - DGL n-ter Ordnung (Differentialgleichungen) - DGL-Gleichungssystem - Mengenelemente - Venn-Diagramm - Zahluntersuchung - Bruchrechnung - Primzahlen - Sieb des Eratosthenes - Taschenrechner - Langarithmetik - Einheitskreis komplexer Zahlen - Schreibweisen komplexer Zahlen - Berechnungen mit komplexen Zahlen - Addition komplexer Zahlen - Multiplikation komplexer Zahlen - Taschenrechner für komplexe Zahlen - Zahlen I - Zahlen II - Zahlensysteme - Zahlumwandlung - P-adische Brüche - Bruch - Dezimalzahl - Kettenbruch - Binomische Formel - Addition - Subtraktion - Irrationale Zahlen - Wurzellupe - Dezimalbruch - Mittelwerte
 

 

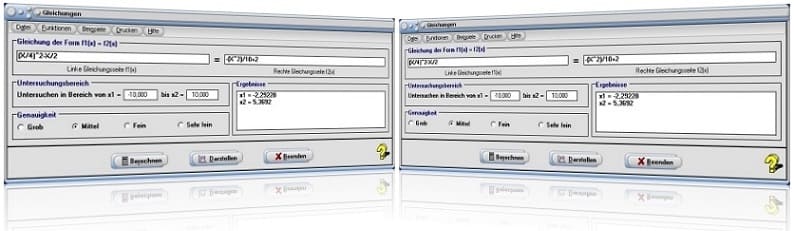
Startfenster des Unterprogramms Gleichungen
 

MathProf 5.0 - Unterprogramm Gleichungen 2. - 4. Grades

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---