MathProf - Geraden - Punkte - Abstand - Gerade - Halbgerade - Strahl

Modul Gerade - Punkt - Interaktiv

---

 
Mit Hilfe des Unterprogramms [Geometrie] - [Gerade] - Gerade - Punkt - Interaktiv können Untersuchungen mit Punkten und Geraden (linearen Funktionen) interaktiv durchgeführt werden.

 

In diesem Modul können folgende Untersuchungen durchgeführt werden:

• Ermittlung des Abstands eines Punktes von einer Geraden (Abstand Punkt-Gerade)
• Ermittlung der Gleichung der Lotgeraden durch einen Punkt auf eine Gerade, sowie Ermittlung des entsprechenden Lotfußpunkts
• Ermittlung der Gleichung der Parallelen zu einer Geraden durch einen externen Punkt

 
Zudem werden folgende Eigenschaften der Geraden ermittelt und ausgegeben:

• Funktionsgleichungen der Geraden
• Nullstellen der Geraden
• Neigungswinkel der Geraden bzgl. der Abszisse
• Abstand der Geraden vom Koordinatenursprung

 
Geradengleichungen (Funktionsgleichungen) können in diesem Modul in einer der nachfolgend aufgeführten Formen definiert werden:
 
1. Steigungs-Form der Gerade
 
  y = m·x+b

2. Zwei-Punkte-Form der Gerade
 

3. Hessesche Normalenform der Gerade
 
  x·cos(β)+y·sin(β) = p

4. Achsenabschnittsform der Gerade
  

5. Allgemeine Form der Gerade

   a·x + b·y + c = 0
 

 
Allgemein gilt für die Berechnung des Abstands eines Punktes P(x;y) von einer Geraden der Form Ax + By + C = 0 folgender Zusammenhang:
 

 

 
Nachfolgend aufgeführt sind einige Grundbegriffe, die in der Planimetrie in einer gegebenen Ebene von Bedeutung sind.

Punkt: Bei einem Punkt P handelt es sich um ein Objekt, welches sich auf einer Ebene befindet. Ein Punkt ist geometrisches Objekt, welches keine Ausdehnung besitzt.


Gerade: Eine Gerade g besteht aus unendlich vielen Punkten. Sie ist durch zwei auf ihr liegende Punkte eindeutig bestimmt.


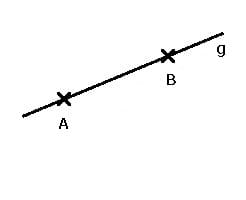
Strecke: Eine Strecke AB ist die Menge aller Punkte einer Gerade g, die zwischen den Punkten A und B liegen. Die Endpunkte A und B zählen zur Punktmenge.


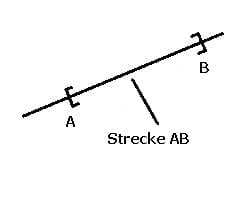
Halbebene: Eine Ebene wird durch eine Gerade, die auf dieser liegt, in zwei Teile geteilt. Die Gerade selbst ist eine Teilmenge dieser Halbebenen.


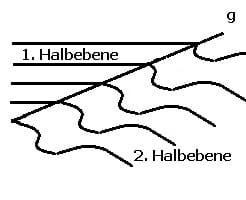
Halbgerade: Ein Punkt P teilt eine Gerade g in zwei Halbgeraden g1 und g2.


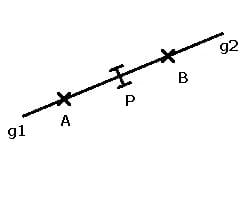
Strahl: Unter einem Strahl wird eine gerichtete Halbgerade verstanden.


Pfeil: Unter einem Pfeil wird eine gerichtete Strecke verstanden.
 

 
Gehen Sie folgendermaßen vor, um Untersuchungen mit Geraden und Punkten durchzuführen:
 

1. Benutzen Sie die aufklappbare Auswahlbox, um die Art der Gerade g festzulegen, mit welcher Untersuchungen durchzuführen sind (zur Auswahl stehen: Steigungsform, 2-Punkte-Form, Hessesche Normalenform, Achsenabschnittsform, Allgemeine Form).
    
2. Stellen Sie hierauf mit den zur Verfügung stehenden Schiebereglern (falls vorhanden) auf dem Bedienformular die Werte für die entsprechenden Größen der Geraden ein (Gerade in Steigungsform: Steigung m ; Gerade in Hessescher Normalenform: Winkel β und Koeffizient p ; Gerade in Achsenabschnittsform: Achsenabschnitte a und b ; Gerade in Allgemeiner Form: Koeffizienten a, b und c).
    
3. Sind zur Definition einer Geraden Punktkoordinaten erforderlich, so können Sie die Schaltfläche Punkte auf dem Bedienformular nutzen und die entsprechenden Werte im daraufhin erscheinenden Formular eingeben. Übernommen werden diese, wenn Sie die sich dort befindende Schaltfläche Ok bedienen.
   
   Möchten Sie die Lage eines Geradenpunktes mit der Maus verändern, so klicken Sie mit der linken Maustaste in den rechteckig umrahmten Mausfangbereich und bewegen den Mauscursor bei gedrückt gehaltener Maustaste.
    
4. Legen Sie durch die Aktivierung des dafür vorgesehenen Kontrollschalters fest, welche Untersuchungsart Sie durchführen möchten. Um den Abstand eines Punkte von einer Geraden ermitteln zu lassen, wählen Sie den Kontrollschalter Abstand Punkt - Gerade. Soll die Gleichung einer Lotgeraden zu einer Geraden durch einen Punkt ausgegeben werden, aktivieren Sie den Kontrollschalter Lot Punkt - Gerade. Die Parallele durch einen Punkt zu einer Geraden wird ermittelt, wenn Sie den Kontrollschalter Parallele Punkt - Gerade wählen.
    
5. Um Zusammenhänge mit Hilfe von Simulationen zu analysieren, bedienen Sie die Schaltfläche Simulation. Vor dem Start einer Simulation wird Ihnen ein Formular zur Verfügung gestellt, auf welchem Sie die zu simulierende Größe durch eine Aktivierung des entsprechenden Kontrollschalters festlegen. Hierauf können Sie ggf. den Wert für die Schrittweite bzw. die Anzahl zu verwendender Winkelschritte einstellen. Bestätigen Sie mit Ok. Beendet werden kann die Ausführung einer derartigen Simulation wieder durch eine erneute Betätigung dieser Schaltfläche. Sie trägt nun die Bezeichnung Sim. Stop.

 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

 

Auf dem Bedienformular, welches durch Anklicken im obersten schmalen Bereich und bei Gedrückthalten der linken Maustaste verschiebbar ist, können Sie u.a. durch die Aktivierung bzw. Deaktivierung der entsprechenden Kontrollkästchen folgende zusätzliche Einstellungen vornehmen:
 

• Lotfußpunkt: Darstellung des Lotfußpunkts ein-/ausschalten
• Lotstrecke: Darstellung der Lotstrecke ein-/ausschalten
• Punkte: Darstellung markanter Punkte ein-/ausschalten
• Koordinaten: Koordinatenwertanzeige markanter Punkte ein-/ausschalten

 

 

Allgemeines zum Handling des Programms bzgl. der Darstellung zweidimensionaler Grafiken wird unter Zweidimensionale Grafiken - Handling beschrieben. Wie Sie das Layout einer 2D-Darstellung konfigurieren können, erfahren Sie unter Layoutkonfiguration. Methoden zur Implementierung und zum Umgang mit grafischen Objekten werden unter Implementierung und Verwendung grafischer Objekte behandelt.

 

 

Gerade - Punkt

Gerade - Gerade

Gerade - Gerade - Interaktiv

Achsenabschnittsform einer Geraden

Punkt-Richtungs-Form einer Geraden

Zwei-Punkte-Form einer Geraden

Hessesche Normalenform einer Geraden

Allgemeine Form einer Geraden

Geradensteigung

 

 
Beispiel 1 - Abstand Punkt-Gerade:

Wird der Kontrollschalter Abstand Punkt - Gerade aktiviert und wird aus der Auswahlbox der Eintrag 2-Punkte-Form gewählt, so ermittelt das Programm nach Festlegung der Koordinatenwerte der Geradenpunkte A (1 / 2) und B (3 / 3), sowie der Definition des Punktes P (-3 / 5), nach einem Klick auf die Schaltfläche Punkte, folgende Ergebnisse:

Abstand des Punktes P von der Gerade: d = 4,472

 

Für die Eigenschaften der Gerade:

Gleichung der Gerade in Normalform (Steigungsform): Y = 0,5·X+1,5

Gleichung der Gerade in allgemeiner Form: 0,5·X - 1·Y + 1,5 = 0

Steigungswinkel der Gerade: 26,565°

Abstand der Gerade vom Ursprung: d = 1,342

Nullstelle der Gerade: N (-3 / 0)

 

Lotfußpunkt: L (-1 / 1)
 

Beispiel 2 - Lot Punkt-Gerade:

Eine Gerade g besitze die Steigung m = 2 und verlaufe durch Punkt A (6 / 4). Es gilt, die Lotgerade zu dieser Gerade zu bestimmen, welche durch Punkt P (7 / -2) verläuft.

Vorgehensweise und Lösung:

Es wird der Kontrollschalter Lot Punkt - Gerade aktiviert und aus der Auswahlbox der Eintrag Steigungsform gewählt. Nach einer Positionierung des Schiebereglers m, zur Definition der Steigung der Gerade g, auf den Wert m = 2, sowie einer Bedienung der Schaltfläche Punkte und der Eingabe der Koordinatenwerte der Punkte A und B, gibt das Programm aus:

Abstand des Punktes P von der Gerade: d = 3,578

 

Für die Eigenschaften der Gerade:

Gleichung der Gerade in Normalform (Steigungsform): Y = 2·X-8

Gleichung der Gerade in allgemeiner Form: 2·X - 1·Y - 8 = 0

Steigungswinkel der Gerade: 63,435°

Abstand der Gerade vom Ursprung: d = 3,578

Nullstelle der Gerade: N (4 / 0)

 

Lotfußpunkt: L (3,8 / -0,4)

 

Die Gleichung der Lotgeraden durch Punkt P lautet: Y = -0,5·X + 1,5
 

Beispiel 3 - Parallele Punkt-Gerade:

Eine Gerade wird durch die Gleichung 10·x - 4·y - 3 = 0 beschrieben. Es gilt, die Parallele zu dieser Geraden zu bestimmen, die durch den Punkt P (8 / 4) verläuft.

Vorgehensweise und Lösung:

Hierzu wird der Kontrollschalter Parallele Punkt - Gerade aktiviert und aus der Auswahlbox der Eintrag Allgemeine Form gewählt. Nach einer Positionierung der Schieberegler a, b und c, zur Definition der Gerade g, auf die Werte a = 10, b = -4 und c = -3, sowie einer Bedienung der Schaltfläche Punkte und der Eingabe der Koordinatenwerte des Punkts P, gibt das Programm aus:

Abstand des Punktes P von der Gerade: d = 5,664

 

Für die Eigenschaften der Gerade:

Gleichung der Gerade: 10·x - 4·y - 3 = 0

Steigungswinkel der Gerade: 68,199°

Abstand der Gerade vom Ursprung: d = 0,279

Nullstelle der Gerade: N (0,3 / 0)

 

Lotfußpunkt: L (2,741 / 6,103)

 

Die Gleichung der Parallelen durch Punkt P zur Geraden 10·x - 4·y - 3 = 0

lautet: Y = 2,5·X - 16
 

 

Grafische Darstellung - Beispiel 1


Grafische Darstellung - Beispiel 2


Grafische Darstellung - Beispiel 3


Grafische Darstellung - Beispiel 4


Grafische Darstellung - Beispiel 5
   

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
   

 

Hilfreiche Informationen zu diesem Fachthema sind unter folgenden Adressen zu finden.

Wikipedia - Lineare Funktion
Wikipedia - Achsenabschnittsform
Wikipedia - Punktsteigungsform
Wikipedia - Zweipunkte-Form
Wikipedia - Hessesche Normalenform
 

 

Achsenabschnittsform einer Geraden - Punkt-Richtungs-Form einer Geraden - Zwei-Punkte-Form einer Geraden - Hessesche Normalenform einer Geraden - Allgemeine Form einer Gerade - Gerade - Gerade - Gerade - Gerade - Interaktiv - Gerade - Punkt - Geradensteigung - Kreis - Punkt - Kreis - Punkt - Interaktiv - Kreis - Gerade - Kreis - Gerade - Interaktiv - Kreis - Kreis - Kreis - Kreis - Interaktiv - Kreisausschnitt - Kreissegment - Kreisring - Ellipse - Regelmäßiges Vieleck - Viereck - Allgemeines Viereck – Interaktiv - Satz des Ptolemäus - Satz des Arbelos - Pappus-Kreise - Archimedische Kreise - Hippokrates Möndchen - Varignon-Parallelogramm - Rechteck-Scherung - Soddy-Kreise - Polygone - Bewegungen in der Ebene - Affine Abbildung - Analyse affiner Abbildungen - Inversion einer Geraden am Kreis - Inversion eines Kreises am Kreis - Spirolateralkurven - Spiralen im Vieleck - Granvillesche Kurven - Bérard-Kurven - Eikurven - Kegelschnitt - Prinzip - Pyramidenschnitt - Prinzip - Kegelschnitte in Mittelpunktlage - Kegelschnitte in Mittelpunktlage - Interaktiv - Kegelschnitte in achsparalleler Lage - Kegelschnitte in achsparalleler Lage - Interaktiv - Kegelschnitte in Mittelpunktlage - Punkt - Kegelschnitte in Mittelpunktlage - Gerade - Allgemeine Kegelschnitte - Kegelschnitte durch 5 Punkte - Interaktive Geometrie mit Objekten - Winkelmaße - Strahlensatz - Teilungsverhältnis - Konstruktion einer Mittelsenkrechten - Konvexe Hülle - Dreieck - Pyramide - Quader im Raum (3D) - Krummflächig begrenzte Körper (3D) - Ebenflächig und krummflächig begrenzte Körper (3D) - Platonische Körper (3D) - Archimedische Körper (3D) - Spezielle Polyeder (3D) - Selfbuild - Punkte (3D) - Selfbuild - Strecken (3D)

 

MathProf 5.0 - Unterprogramm Gerade - Gerade

---

MathProf 5.0 - Unterprogramm Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---