MathProf - Normalform - Paraboloid - Ellipsoid - Hyperboloid - Plotter

Modul Flächen 2. Ordnung - Interaktiv

---

Im Unterprogramm [3D-Mathematik]- [Flächen 2. Ordnung] - Flächen 2. Ordnung - Interaktiv können Flächen 2. Ordnung, welche in erster oder zweiter Normalform definiert sind, grafisch dargestellt werden und Zusammenhänge zu diesem Fachthema interaktiv untersucht werden.

 

 

Das Modul ermöglicht:
 

• Interaktive Analyse der Art von Flächen 2. Ordnung, welche in 1. oder 2. Normalform definiert sind
• Interaktive Darstellung von Flächen 2. Ordnung, welche in 1. oder 2. Normalform definiert sind

   
Die allgemeine Funktionsgleichung
 
Ax²+By²+Cz²+2Dxy+2Exz+Fyz+2Gx+2Hy+2Iz+K = 0
 
stellt eine algebraische Gleichung 2. Ordnung dar, wobei A, B, C, D, E, F, G, H, I  und K beliebige reelle Koeffizienten sind.
 
Durch eine Hauptachsentransformation und weitere Koordinatentransformationen, mit welcher die Ausrichtung der Achsen der Flächen parallel zu den Koordinatenachsen erlangt wird, erreicht man die Darstellung einer Fläche 2. Ordnung in Normalform, die sich in zwei Arten gliedert:
 
1. Normalform:
 

 
2. Normalform:
 

 
Die Normalformen dieser Flächen 2. Ordnung zur Beschreibung der Kegelschnitte in allgemeiner achsparalleler Lage im Raum lauten:
 
1. Normalform:
 

 
2. Normalform:
 

 
Dieses Modul ermöglicht die Analyse der Zusammenhänge und die Darstellung der Flächen, welche durch derartige Gleichungen beschrieben werden. Hierbei sind die Werte für die Koeffizienten a, b, c, die Verschiebungsparameter x₀, y₀, z₀ sowie der reelle Zahlenwert des Absolutglieds m frei wählbar.  
 

 
Eine Fläche 2. Ordnung (Quadrik) ist die Menge aller Punkte eines dreidimensionalen Raumes, deren Koordinaten einer quadratischen Gleichung genügen. Sie wird als die Lösungsmenge einer quadratischen Gleichung bezeichnet, die mehrere Variablen besitzt.
 
Die allgemeine Funktionsgleichung einer Fläche dieser Art lautet:

 

Ax²+By²+Cz²+2Dxy+2Exz+Fyz+2Gx+2Hy+2Iz+K = 0

 

Sie stellt eine algebraische Gleichung 2. Ordnung dar, wobei A, B, C, D, E, F, G, H, I  und K beliebige reelle Koeffizienten sind.

 

Durch eine Hauptachsentransformation und weitere Koordinatentransformationen, mit welcher die Ausrichtung der Achsen der Flächen parallel zu den Koordinatenachsen erlangt wird, erreicht man die Darstellung einer Fläche 2. Ordnung in Normalform, die sich in zwei Arten gliedert:

 

1. Normalform:

 

 

2. Normalform:

 

 

Die Normalformen dieser Flächen 2. Ordnung zur Beschreibung der Kegelschnitte in allgemeiner achsparalleler Lage im Raum lauten:

 

1. Normalform:

 

 

2. Normalform:

 

 

 

Echte und entartete Flächen 2. Ordnung könnnen wie folgt eingeteilt werden:
 

• Reelles Ellipsoid

• Einschaliges Hyperboloid

• Zweischaliges Hyperboloid

• Elliptischer Doppelkegel

• Elliptischer Zylinder

• Hyperbolischer Zylinder

• Elliptisches Paraboloid

• Hyperbolisches Paraboloid

• Parabolischer Zylinder

• Zwei sich schneidende Ebenen

• Zwei parallele Ebenen

• Eine Ebene (y-z-Ebene)

• Punkt (entartetes Ellipsoid)

• Imaginärer elliptischer Zylinder

• Zwei sich imaginär schneidende Ebenen

• Imaginäres Ellipsoid

• Fläche 2. Ordnung, nullteilig

Nachfolgend aufgeführt sind Gleichungen für echte Flächen zweiten Grades sowie für Entartungsfälle (unechte Flächen zweiten Grades).

Echte Flächen zweiten Grades:
  

Gleichung	Art
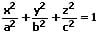	Ellipsoid mit Mittelpunkt M(0|0|0)
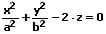	Elliptisches Paraboloid
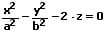	Hyperbolisches Paraboloid
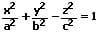	Einschaliges Hyperboloid für a ≠ b
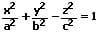	Einschaliges Rotationshyperboloid für a = b
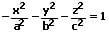	Zweischaliges Hyperboloid für a ≠ b
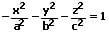	Zweischaliges Rotationshyperboloid für a = b

 
Entartete Kegelschnitte:
  

Gleichung	Art
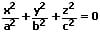	Punkt (0|0|0)
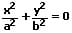	z-Achse (Gerade)
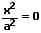	y,z-Ebene
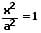	Zwei zur y,z-Ebene parallele Ebenen, x = ± a
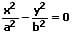	Zwei Ebenen, welche die x,y-Ebene mit zwei parallelen Geraden vertikal schneiden
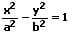	Mantelfläche eines Zylinders, welche von Ebenen zwei senkrecht zur z-Achse in Hyperbeln geschnitten wird
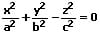	Mantelfläche eines Doppelkegels, welche von zwei Ebenen senkrecht zur z-Achse in Ellipsen geschnitten wird
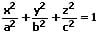	Mantelfläche eines Zylinders, welche von Ebenen senkrecht zur z-Achse in Parabeln geschnitten wird

 

Das Ellipsoid zählt zu den Flächen zweiter Ordnung. Es ist die dreidimensionale Entsprechung einer Ellipse. Sie entspricht dem affinen Bild der Einheitskugel, die sich mit der nachfolgend gezeigten Gleichung beschreiben lässt. x^2+y^2+z^2 = 1.

Das Hyperboloid zählt zu den Flächen zweiter Ordnung. Es handelt sich um eine Fläche, die mittels Ebenen in Hyperbeln, Ellipsen, Parabeln geschnitten (zerlegt) werden kann. Unterschieden wird zwischen einem einschaligen und einem zweischaligen Hyperboloid.

Ein Paraboloid ist eine Fläche zweiter Ordnung (Quadrik). Es handelt sich um einen Körper, der entsteht, wenn eine Parabel im Raum um ihre eigene Achse rotiert. Unterschieden wird zwischen dem elliptischen und dem hyperbolischen Paraboloid.
 

Grafische Darstellung - Beispiel 1 - Zweischaliges Hyperboloid
 

Grafische Darstellung - Beispiel 2 - Hyperbolischer Zylinder


Grafische Darstellung - Beispiel 3 - Einschaliges Hyperboloid
 

 

Nachfolgend finden Sie ein Video zu diesem Fachthema, welches Sie durch die Ausführung eines Klicks
auf die nachfolgend gezeigte Grafik abspielen lassen können.

 

 

Es wird ein dem nachfolgend gezeigten, ähnliches Bedienformular zur Verfügung gestellt, welches die Veränderung von Punktkoordinatenwerten, bzw. Koeffizienten mit Hilfe von Rollbalken zulässt.
 

 
Die Parameter folgender Einflussgrößen können durch manuelle oder simulative Veränderung der Position von Rollbalken eingestellt werden:

 
Gehen Sie folgendermaßen vor, um Zusammenhänge zu oben beschriebenen Sachverhalten interaktiv zu analysieren:
 

1. Selektieren Sie den Menüpunkt Grafische Analyse / Vorgabeeinstellung (voreingestellt).
    
2. Wählen Sie durch die Aktivierung des Kontrollschalters 1. Normalform bzw. 2. Normalform, ob Untersuchungen mit Kegelschnittgleichungen 1. Normalform oder mit Kegelschnittgleichungen 2. Normalform durchgeführt werden sollen.
    
3. Aktivieren Sie Kontrollschalter Interaktiv I oder Interaktiv II.
    
4. Bedienen Sie die Schaltfläche Darstellen.
    
5. Nutzen Sie die auf dem Bedienformular zur Verfügung stehenden Schieberegler, um Koeffizientenwerte der Gleichung zur Defintion der Fläche zu verändern.
    
6. Wurde die Darstellungsart Interaktiv II gewählt, so bedienen Sie ggf. den Schieberegler Bereich, um die Größe des Darstellungsbereichs festzulegen.
    
7. Starten Sie bei Bedarf eine Autosimulation mit dem Schalter Start Sim. Diese Schaltfläche trägt hierauf die Bezeichnung Stop Sim. Angehalten werden kann die Simulation durch eine erneute Betätigung dieser.

Hinweise:
Vor dem Start einer Simulation wird ein Formular zur Verfügung gestellt, auf welchem Sie durch eine Aktivierung der entsprechenden Kontrollkästchen die Auswahl simulativ zu verändernder Einflussgrößen (Koordinatenwerte) treffen.

Bei jeder Veränderung einer Rollbalkenposition werden die Ergebnisse durchgeführter Berechnungen ausgegeben (unter der Voraussetzung, dass Textausgabe eingeschaltet ist).
   

 
Das Programm ermöglicht die Abtastung der Kontur einer dargestellten Fläche und somit die Analyse von Koordinatenwerten. Hierfür stehen die Rollbalken mit den Bezeichnungen Pos. 1 und Pos. 2 zur Verfügung, mit welchen Sie die Abtastposition auf der Kontur der Fläche, je nach Lage des Objekts, in zwei Richtungen steuern können. Die Koordinatenwerte werden an der entsprechenden Position ausgegeben. Ist an der untersuchten Stelle kein Kegelschnitt definiert, oder liegt der zu analysierende Bereich außerhalb des eingestellten Darstellungsbereichs, so wird dies angezeigt.
 
Um eine Wertebereichsanalyse durchzuführen, aktivieren Sie vor Aufruf der Darstellung den Menüeintrag Grafische Analyse / Koordinatenwertanalyse. Um diesen Modus wieder auszuschalten, wählen Sie den Menüeintrag Grafische Analyse / Vorgabeeinstellung.
   
Das Programm stellt hierbei die folgenden beiden Möglichkeiten zur Verfügung, um interaktive Analysen von Sachverhalten und Zusammenhängen zu diesem Fachthema durchzuführen:
 

• Interaktiv I
• Interaktiv II

Wird der Kontrollschalter Interakiv I aktiviert, so wird der Darstellungsbereich, abhängig von vorgegebenen Werten, vom Programm automatisch festgelegt.

Bei einer Aktivierung des Kontrollschalters Interakiv II stellt es die Zusammenhänge innerhalb eines durch Zahlenwerteingaben festlegbaren Bereichs dar. Alle auszugebenden Objekte werden in diesem Fall an den Grenzen des eingestellten Darstellungsbereichs beschnitten. Befinden sich hierbei Teile eines Objekts außerhalb des gewählten Darstellungsbereichs und ist dieses hierdurch nicht mehr vollständig sichtbar, so ist der zur Erreichung einer korrekten Ausgabe erforderliche Darstellungsbereich mit Hilfe des zur Verfügung stehenden Rollbalkens Bereich einzustellen.
   
Grundlegendes zum Umgang mit dem Programm bei der Ausgabe dreidimensionaler grafischer Darstellungen erfahren Sie unter Dreidimensionale Grafiken - Handling. Wie Sie das Layout einer 3D-Darstellung konfigurieren können, erfahren Sie unter 3D-Layoutkonfiguration.
   
Flächen 2. Ordnung (3D)
   
Beispiel 1 -1. Normalform:
 
Um sich eine Fläche 2. Ordnung darstellen zu lassen, welche durch nachfolgende Gleichung in 1. Normalform beschrieben wird
 

 
aktivieren Sie auf dem Hauptformular des Unterprogramms den Kontrollschalter 1. Normalform und positionieren die Rollbalken wie folgt:
 
a: 2
b: -2
c: -4
 
m: 5
 
x₀: 0
y₀: 0
z₀: 0
 
Das Programm stellt hierbei u.a. fest, dass durch diese Gleichung ein zweischaliges Hyperboloid beschrieben wird.
 
Beispiel 2 - 2. Normalform:
 
Um sich eine Fläche 2. Ordnung ausgeben zu lassen, welche durch nachfolgende Gleichung in 2. Normalform beschrieben wird
 

 
aktivieren Sie auf dem Hauptformular des Unterprogramms den Kontrollschalter 2. Normalform und positionieren die Rollbalken wie folgt:
 
a: -6
b: -5
c: 2
 
m: 0
 
x₀: 1
y₀: 3
z₀: -2
 
Das Programm gibt aus, dass durch diese Gleichung ein elliptisches Paraboloid beschrieben wird.
 

 
Mit Hilfe dieses Programms lassen sich unter anderem Grafiken für Arbeitsblätter zur nichtkommerziellen Nutzung für Unterrichtszwecke erstellen. Beachten Sie hierbei jedoch, dass jede Art gewerblicher Nutzung dieser Grafiken und Texte untersagt ist und dass Sie zur Verfielfältigung hiermit erstellter Arbeitsblätter und Unterrichtsmaterialien eine schriftliche Genehmigung des Autors (unseres Unternehmens) benötigen.

Diese kann von einem registrierten Kunden, der im Besitz einer gültigen Softwarelizenz für das entsprechende Programm ist, bei Bedarf unter der ausdrücklichen Schilderung des beabsichtigten Verfielfältigungszwecks sowie der Angabe der Anzahl zu verfielfältigender Exemplare für das entsprechende Arbeitsblatt unter der auf der Impressum-Seite dieses Angebots angegebenen Email-Adresse eingeholt werden. Es gelten unsere AGB.
 

  
Dieses Programm eignet sich neben seinem Einsatz als Berechnungs- bzw. Animationsprogramm zudem zum Lernen, zur Aneignung entsprechenden Fachwissens, zum Verstehen sowie zum Lösen verschiedener Aufgaben zum behandelten Fachthema. Durch seine einfache interaktive Handhabbarkeit bietet es die auch Möglichkeit der Durchführung unterschiedlicher Untersuchungen hierzu.

Es kann sowohl zur Einführung in das entsprechende Fachthemengebiet, wie auch zur Erweiterung des bereits hierzu erlangten Fachwissens sowie als Unterstützung bei der Bearbeitung von Anwendungsaufgaben genutzt werden. Des Weiteren eignet es sich auch als Begleiter bei der Bearbeitung von Abituraufgaben sowie zur Vorbereitung auf Klassenarbeiten, zur Unterstützung bei der Abiturvorbereitung und zur Intensivierung des erforderlichen Wissens beim Abitur (Abi) im entsprechenden Leistungskurs (LK).

Mittels der anschaulichen Gestaltung und einfachen Bedienbarbarkeit einzelner Module dieser Software können Fragen zum entsprechenden Themengebiet, die mit den Worten Was ist?, Was sind?, Wie?, Wieviel?, Was bedeutet?, Weshalb?, Warum? beginnen beantwortet werden.

Eine mathematische Herleitung dient dazu, zu erklären, weshalb es zu einer Aussage kommt. Derartige Folgerungen sind unter anderem dazu dienlich, um zu verstehen, weshalb eine Formel bzw. Funktion Verwendung finden kann. Dieses Modul kann auch in diesem Fall hilfreich sein und ermöglicht es durch dessen Nutzung oftmals, einer entsprechenden Herleitung bzw. einem mathematischen Beweis zu folgen, oder einen Begriff zum entsprechenden Fachthema zu erklären.

Bei Fragen deren Wörter Welche?, Welcher?, Welches?, Wodurch? bzw. Wie rechnet man? oder Wie berechnet man? sind, können zugrunde liegende Sachverhalte oftmals einfach erklärt und nachvollzogen werden. Auch liefert diese Applikation zu vielen fachthemenbezogenen Problemen eine Antwort und stellt eine diesbezüglich verständliche Beschreibung bzw. Erklärung bereit.

  

 

Grafische Darstellung - Beispiel 4


Grafische Darstellung - Beispiel 5


Grafische Darstellung - Beispiel 6
 

Eine kleine Übersicht in Form von Bildern und kurzen Beschreibungen über einige zu den einzelnen Fachthemengebieten dieses Programms implementierte Unterprogramme finden Sie unter Screenshots zum Themengebiet Analysis - Screenshots zum Themengebiet Geometrie - Screenshots zum Themengebiet Trigonometrie - Screenshots zum Themengebiet Algebra - Screenshots zum Themengebiet 3D-Mathematik - Screenshots zum Themengebiet Stochastik - Screenshots zum Themengebiet Vektoralgebra sowie unter Screenshots zu sonstigen Themengebieten.
 

 

Hilfreiche Informationen zu diesem Fachthema sind unter Wikipedia - Quadrik sowie unter Wikipedia - Kegelschnitt zu finden.

 

 

Rotation von Kurven in Parameterform um die X-Achse (3D) - Rotation von Kurven in kartesischer Form um die Y-Achse (3D) - Rotation von Kurven in Parameterform um die Y-Achse (3D) - Flächen mit Funktion in expliziter Form (3D) - Analyse implizit definierter Funktionen (3D) - Flächen mit Funktionen in Parameterform (3D) - Funktionen in sphärischen Kugelkoordinaten (3D) - Funktionen in sphärischen Zylinderkoordinaten (3D) - Raumkurven in Parameterform (3D) - Flächen 2. Ordnung (3D) - Rotation von Kurven in Polarform um die X-Achse (3D) - Rotation von Kurven in Polarform um die Y-Achse (3D) - Untersuchungen mit Flächen in expliziter Form (3D) - Untersuchungen mit Raumkurven in Parameterform (3D) - Flächen implizit definierter Funktionen (3D) - Konturen implizit definierter Funktionen (3D) - Schnittkurven von Flächen mit Funktionen in expliziter Form (3D) - Schnittkurven von Flächen mit Funktionen in Parameterform (3D) - Schnittkurven von Funktionen in sphärischen Zylinderkoordinaten (3D) - Tangentialebenen von Flächen mit Funktionen in Parameterform (3D) 

 

Startfenster des Unterprogramms Flächen 2. Ordnung - Interaktiv
 

MathProf 5.0 - Startfenster des Unterprogramms Raumkurven

---

MathProf 5.0 - Grafikfenster des Unterprogramms Kurven von Funktionen in Parameterform
 

 

PhysProf 1.1 - Unterprogramm Adiabatische Zustandsänderung
 

SimPlot 1.0 - Grafik-  und Animationsprogramm für unterschiedlichste Anwendungszwecke

 

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

Nachfolgend finden Sie ein Video zu einer mit SimPlot 1.0 erstellten Animationsgrafik, welches Sie durch die Ausführung eines Klicks auf die nachfolgend gezeigte Grafik abspielen lassen können.

---